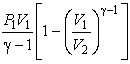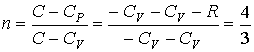Как найти работу газа при адиабатном процессе

Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Что это адиабатический процесс?

Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

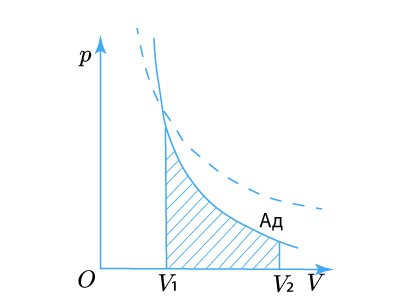
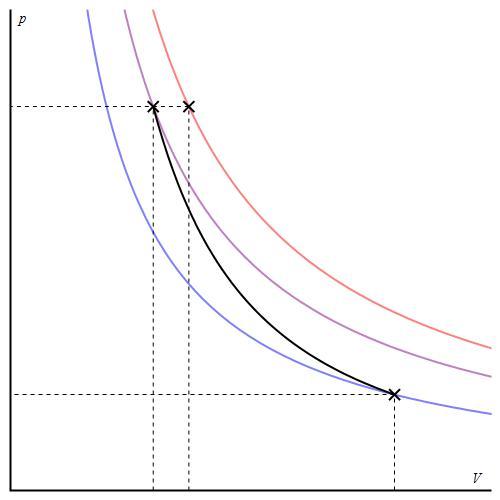
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Пример задачи

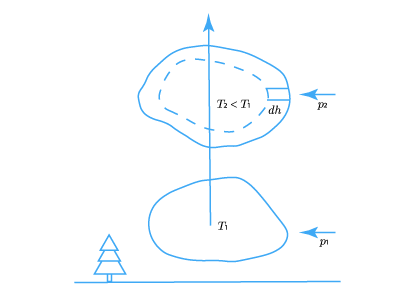
В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.

2.4. Адиабатный процесс

Адиабатный процесс — это процесс, при котором не происходит теплообмена с внешней средой.

Физически это означает, что процесс протекает достаточно быстро и система не успевает обменяться теплотой с внешними телами. Однако коль скоро мы имеем дело с равновесными процессами, скорость адиабатного процесса не должна быть слишком уж велика. Примером таких процессов может служить распространение звуковых колебаний в упругой среде.

Выведем уравнение, описывающее адиабатный процесс. Ранее мы имели дело с самыми простыми уравнениями процессов

— для изотермического процесса;

— для изобарного процесса;

— для изохорного процесса.

Поскольку в адиабатном процессе dQ = 0, из первого начала термодинамики следует, что

C другой стороны,

Приравнивая эти выражения, находим

Умножая уравнение (2.28) на V g –1 , получаем в левой части полный дифференциал

В результате интегрирования (2.29) приходим к уравнению адиабатного процесса

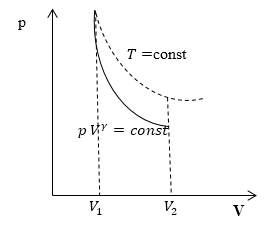
Графически адиабатный процесс описывается на (р,V) — диаграмме кривыми, похожими на изотермы (рис. 2.12), но идущими круче, так как g > 1, поскольку С_p > С_V.

Рис. 2.12. Адиабатный процесс в идеальном газе: 1 — адиабата, 2 — изотерма

Это и понятно, так как при адиабатном расширении газ совершает работу за счет внутренней энергии, и его температура падает, что еще больше уменьшает давление по сравнению с изотермическим расширением.

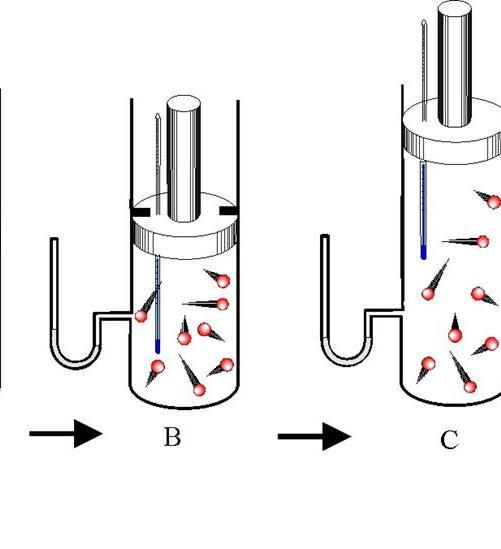
Экспериментальное исследование адиабатного процесса в идеальном газе можно выполнить с помощью установки, представленной на рис. 2.13.

Рис. 2.13. Экспериментальное изучение адиабатного процесса в идеальном газе

Учитывая, что из уравнения состояния идеального газа следует пропорциональность

уравнение адиабатного процесса можно также представить в виде

Первый закон термодинамики в применении к адиабатному процессу позволяет вычислить работу газа при адиабатном расширении:

Выражения для работы при адиабатном процессе с учетом уравнения Клапейрона — Менделеева можно выразить также через температуры в начале и конце процесса

Для бесконечно малых изменений параметров уравнения (2.32), (2.33) переходят в соотношения

Пример. Горючая смесь в двигателе Дизеля (см. рисунок выше) воспламеняется при температуре Т₂ = 1 100 К. Начальная температура смеси Т₁ = 350 К. Определим, во сколько раз нужно уменьшить объем смеси при сжатии, чтобы она воспламенилась. Сжатие будем считать адиабатным. Показатель адиабаты для смеси g = 1,4.

Для решения удобнее воспользоваться уравнением адиабатного процесса в форме (2.31):

Отсюда сразу следует выражение для степени сжатия горючей смеси:

Адиабатический процесс

Вы будете перенаправлены на Автор24

Что такое адиабатический процесс

Адиабатическим или адиабатным процессом называют процесс, при котором отсутствует теплообмен с окружающей средой ($delta Q=0$).

В таком случае первое начало термодинамики можно записать в виде:

[0=frac<2>nu RdT+pdV left(1right).]

Из уравнения (1) следует, что при увеличении объема в адиабатном процессе уменьшается температура системы. Или говорят, что в адиабатном процессе работа совершается за счет уменьшения внутренней энергии системы. И обратное справедливо: работа, совершенная над системой, увеличивает внутреннюю энергию системы и, как следствие, температуру. Уравнение, которое характеризует адиабатный процесс в термодинамических параметрах (уравнение адиабаты) носит имя Пуассона. Получим это уравнение для идеального газа. Из уравнения состояния идеального газа:

Из соотношения Майера:

[C_p-C_V=nu R left(3right).]

Подставим (3) в (2), получим:

Разделим уравнение (1) $C_VT ( C_V=frac<2>нR)$, получим:

где $gamma =frac$ — показатель адиабаты. Проинтегрируем уравнение (5):

где $lnA$- некоторая постоянная.

Потенцируем уравнение (6), получаем:

Уравнение (7) есть уравнение адиабаты в параметрах T,V. Для того, чтобы перейти к уравнению адиабаты, в параметрах p,V используют уравнение Менделеева — Клайперона. И получают уравнение адиабаты в виде:

Или в параметрах p,T уравнение (7,8) имеет вид:

Зная, что теплоемкости можно представить как:

показатель адиабаты исходя из ($gamma =frac$) и уравнений (10)

Легко получить формулу работы для адиабатного процесса. По определению работа газа A равна:

где $p_1V_1=nu RT_1.$ Используя уравнение адиабаты, записанное для двух состояний в параметрах $V,T$, получаем:

Что такое адиабата

Линия, изображающая на термодинамической диаграмме адиабатный процесс, называется адиабатой (рис.1).

Для сравнения на рис. 1 представлена также изотерма (пунктиром). На рис. 1 видно, что адиабата идет круче, чем изотерма. Работа в адиабатическом процессе по расширению от объема $V_1 $до $V_2$ меньше, чем в изотермическом процессе с таким же изменением объема. Это объясняется тем, что при адиабатном процессе происходит охлаждение газа. В изотермическом процессе при расширении давление уменьшается только за счет уменьшения плотности, тогда как в адиабатном за счет плотности и средней кинетической энергии молекул (соответственно температуры).

Задание: Одноатомный газ совершает адиабатное расширение от объема $V_1=$1$м^3 $при температуре $Т_1=400 К$, при этом давление газа изменяется от $p_1=5cdot <10>^6Па $до $p_2=2cdot <10>^6 Па$. Найдите объем газа в конечном состоянии.

При адиабатном расширении имеем:

где $gamma =frac , $так как газ одноатомный, то i=3, следовательно, $gamma =frac<3+2><3>=frac<5><3>$. Значит можно выразить интересующий нас объем:

Ответ: Объем газа в конечном состоянии 4,6 $м^3.$

Задание: Некоторую массу газа сжали так, что $frac=5$, в первом случае процесс проводился адиабатический, второй изотермический. Начальные состояния газов одинаковы в том и другом случае. Найти отношение работ $frac=?$

Работа в адиабатном процессе задана формулой над газом:

Формула для работы в изотермическом процессе имеет вид:

Тогда найдем искомое отношение:

Для коэффициента адиабаты мы знаем формулу вычисления через число степеней свободы$(i)$, а для одноатомного газа $i=3$:

Подставим данные из условий задачи, получим:

Ответ: Отношение работ, которые совершают над газом в процессах сжатия в адиабатном процессе и изотермическом равно 1,89. Работа над газом в адиабатном процессе больше.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 11 2021

источники:

http://online.mephi.ru/courses/physics/molecular_physics/data/course/2/2.4.1.html

http://spravochnick.ru/fizika/termodinamika/adiabaticheskiy_process/

Адиабатический
процесс — это такое изменение состояний
газа, при котором он не отдает и не
поглощает извне теплоты. Следовательно,
адиабатический процесс характеризуется
отсутствием теплообмена газа с окружающей
средой. Адиабатическими можно считать
быстро протекающие процессы. Так как
передачи теплоты при адиабатическом
процессе не происходит, то  и
уравнение I начала термодинамики
принимает вид

(9.20)

или

т.е.
внешняя работа газа может производиться
вследствие изменения его внутренней
энергии. Адиабатное расширение газа
(dV>0) сопровождается положительной
внешней работой, но при этом внутренняя
энергия уменьшается и газ охлаждается
(dT<0).

Сжатие
газа (dV0, т.е. адиабатное сжатие газа
сопровождается его нагреванием.

Найдем
связь между параметрами состояния
идеального газа (например, Р и V) в
адиабатическом процессе. Для этого
перепишем (9.20) в форме

а
величину  найдем
из уравнения Менделеева — Клапейрона

Таким
образом,

или,
учитывая, что для идеального
газа 

Разделим
обе части этого уравнения на 

где  безразмерная
величина, называемая постоянной адиабаты.
Пренебрегая зависимостью от
температуры, можно считать, что для
данного газа  .
Интегрируя последнее уравнение

получим

т.е.

(9.21)

Это
выражение называют уравнением Пуассона.
Соотношение между давлением и температурой,
а также между объемом и температурой
идеального газа в адиабатическом
процессе имеют вид

Эти
соотношения легко получить из (9.21),
пользуясь уравнением Менделеева —
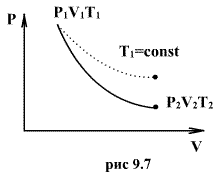
Клапейрона. Линию, изображающую
адиабатический процесс в диаграмме
состояния, называют адиабатой. На рис.
9.7 сплошной линией показан вид адиабаты
в (P-V) диаграмме. Для сравнения в том же
рисунке пунктирной линией изображена
изотерма, соответствующая температуре
газа в начальном состоянии 1. Так как
для любого идеального газа показатель
адиабаты  ,
то в (P-V) диаграмме адиабата всегда идет
круче, чем изотерма. Объясняется это
тем, что при адиабатическом сжатии
увеличение давления обусловлено не
только уменьшением объема газа, как при
изотермическом сжатии, то также еще и
увеличения температуры. При адиабатическом
расширении температура газа уменьшается,
поэтому давление газа падает быстрее,
чем при изотермическом расширении.

Работу,
совершаемую газом в адиабатическом
процессе, найдем интегрируя выражение

Полная
работа

Из
уравнения Майера (9.18) и выражения  для
показателя адиабаты γ следует, что

Поэтому

(9.22)

В
соответствии с соотношением 

Следовательно,
выражение (9.22) для работы можно представить
в виде

или

.6.
Политропический процесс

     В параграфе
2.4 отмечалось,
что важным классом термодинамических
процессов являются процессы, происходящие
при постоянной теплоемкости, то
есть политропические
процессы.
К таким процессам, в частности, относятся
адиабатический, изотермический,
изобарический и изохорический процессы.

     Для
идеального газа нетрудно получить
уравнение политропического процесса
тем же способом, которым ранее было
выведено уравнение Пуассона. Пусть
молярная теплоёмкость идеального газа
в политропическом процессе равна .
Тогда в соответствии с первым началом
термодинамики (1.5) имеем
выражение:

,

(2.99)

     из
которого следует:

.

(2.100)

     Подставляя
это выражение в формулу (2.76) получим

(2.101)

     или
с учетом соотношения Майера (2.70)

.

(2.102)

     Сравнение
формул (2.100) и (2.102) при
условии, что ,
позволяет записать уравнение

,

(2.103)

     аналогичное
уравнению (2.79).
Здесь введен параметр

,

(2.104)

     который
называется показателем
политропы.

     Из
этой формулы можно также получить
зависимость молярной теплоемкости  от
показателя политропы :

.

(2.105)

     Преобразование
формулы (2.103) к
виду:

(2.106)

     и
интегрирование полученного уравнения
дает

.

(2.107)

     Уравнение (2.107) называется уравнением
политропического процесса или политропы –
кривой, описываемой таким уравнением
в переменных  и .

     Аналогично
уравнениям адиабаты (2.86) и (2.87) уравнение
политропы может быть переписано в других
термодинамических координатах:

,

(2.108)

.

(2.109)

     При
адиабатическом процессе ,
что соответствует нулевой теплоемкости.
Подставив  в
формулу (2.104) и
сравнив получившееся выражение с (2.80),
имеем ,
и уравнение политропы (2.107) становится
уравнением адиабаты: .

     Если
процесс изотермический, то ,
так как при этом .
В этом случае показатель политропы  в
пределе равен единице, и уравнение
политропы (2.107) преобразуется
в уравнение Бойля-Мариотта (2.11): .
Обратим внимание на то, что поскольку
при выводе уравнения политропы мы
исключали величину ,
то этот вывод не может считаться полностью
корректным для изотермического процесса.

     Для
изобарического процесса при  показатель
политропы ,
и уравнение (2.107) принимает
форму: .

     При
изохорическом процессе  должно
стать равным ,
что соответствует случаю, когда
показатель .
Очевидно, переход в формуле (2.107) к
указанному пределу некорректен. Это
связано с тем, что при выводе уравнения
политропы предполагалось, что  (см.
переход к формуле (2.103)).

     Если
умножить уравнение (2.100) на
величину  и
сложить его с уравнением (2.102),
предварительно умноженным на величину ,
то получим уравнение политропы в
дифференциальном виде

.

(2.110)

     При  это
уравнение приобретает форме:

(2.111)

     Отсюда
имеем  или .
Из уравнения (2.110) также
следует, что в процессе, при котором ,
давление постоянно: .

     Для
политропических процессов значение
теплоёмкости и, соответственно, показателя
политропы могут принимать любые величины.
Отрицательные значения теплоёмкости,
когда показатель политропы  принимает
значения от единицы до величины g (см.
формулу (2.105)),
соответствуют таким условиям, при
которых внутренняя энергия термодинамической
системы убывает при передаче ей
положительного количества теплоты. Это
может быть осуществлено при принудительном
расширении газа.

     В
соответствии с
формулой (2.100) при  величины  и  имеют
различные знаки, и с ростом объёма газа
его температура, а, следовательно, и
внутренняя энергия, уменьшаются. С этим,
в частности, связано понижение температуры
идеального газа при его адиабатическом
расширении, так как в этом процессе .
Наоборот, при  с
ростом объёма газа его температура
растёт. В соответствии с первым началом
термодинамики этот рост должен быть
обеспечен подводом к системе дополнительного
количества теплоты.

     Рассуждая
аналогичным образом, можно на основании
формулы (2.102) установить
связь между приращениями давления и
температуры. При с
ростом давления температура газа будет
возрастать, а при  —
уменьшаться.

     Работа
газа в политропическом процессе может
быть определена с помощью интеграла (1.13) при
подстановке в него уравнения
политропы(2.107),
аналогично тому, как это сделано в
формуле (2.97):

.

(2.112)

     Интегрирование
в выражении (2.112) дает
формулу для определения работы в
политропическом процессе

,

(2.113)

     где:  и  —
начальные давление и объём газа,  —
его конечный объём.

     Из
этой формулы, в частности, следует, что
работа при расширении газа всегда
остаётся положительной, независимо от
того, какое значение принимает показатель
политропы, больше или меньше единицы.

     Нетрудно
видеть, что для адиабатического процесса
при  выражение (2.113) переходит
в формулу (2.95).
Для изобарического процесса, при ,
выражение (2.113) дает

,

(2.114)

     где
учтено, что при этом процессе .

     Формула (2.113) неприменима
для описания изохорического процесса,
так как при выводе уравнения
политропы (2.103) исключался
случай .
Но из формулы (2.100) очевидно,
что работа газа в изохорическом процессе
равна нулю.

     Другим
процессом, не описывающимся
соотношением (2.113),
является изотермический процесс. Как
было сказано выше, он является предельным
случаем политропического процесса
при .
Работу в изотермическом процессе можно
найти, если в формулу (2.112) в
соответствии с законом Бойля-Мариотта
подставить ,
а затем выполнить интегрирование. Тогда
имеем

(2.115)

     или

,

(2.116)

     где
учтено постоянство температуры в этом
процессе: .

     Поскольку
внутренняя энергия идеального газа не
изменяется в изотермическом процессе,
количество теплоты, полученное газом,
также может быть рассчитано по этой
формуле, то есть в этом процессе .
При изотермическом расширении идеального
газа работа совершается только за счёт
теплоты, подведённой из окружающей
среды.

     В
заключение параграфа запишем все
полученные формулы в единую таблицу
2.1.

Термодинамический процесс	Показательполитропы	Теплоемкость	Работа
Изотермический	1
Изобарический	0
Изохорический			0
Адиабатический		0

     Задача
2.4. Какова молярная теплоёмкость  одноатомного
газа и показатель политропы  для
процесса, в котором работа, совершаемая
газом, в два раза превосходит количество
теплоты, передаваемое ему?

     Решение:
Так как по условию задачи ,
то в соответствии с первым началом
термодинамики имеем:

     или

.

     Тогда,
с учетом одноатомности газа (число
степеней свободы ),
молярную теплоемкость можно определить
по формуле:

 ,

     а
показатель политропы соответственно
будет равен:

     Задача
2.5. Какая работа совершается одним молем
идеального газа в политропическом
процессе с показателем политропы  при
изменении температуры газа на ?

     Решение:
Используя уравнение политропы (2.108):  и
уравнение Клапейрона-Менделеева для
одного моля ,
перепишем (2.113) в
виде:

 .

     Отсюда
имеем:

.

     Следовательно,
работа, совершаемая одном молем идеального
газа в процессе с постоянной теплоёмкостью,
определяется только разностью температур
конечного и начального состояний газа.

     Таким
образом, для идеального газа работа, а,
следовательно, и количество теплоты, в
политропических процессах определяются
только конечным и начальным состояниями
системы, так как путь перехода из одного
состояния в другое определён теплоёмкостью
газа (показателем политропы). Однако
даже при рассмотрении только политропических
процессов, работу и количество теплоты
нельзя считать функцией состояния
системы, так как переход из одного
состояния в другое может быть осуществлен
последовательностью различных
политропических процессов.

     Задача
2.6. Какое количество теплоты передано
одноатомному газу в процессе, описанному
в условии задачи 2.5?

     Решение:
В соответствии с формулой (2.105) имеем:

 .

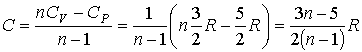
     Тогда
количество теплоты будет равно:

.

     Отсюда,
в частности, следует, что при равенстве
показателя политропы показателю адиабаты
для одноатомного газа: ,
количество теплоты .

Работа
идеального газа в изопроцессах.

Первый
закон термодинамики (закон сохранения
энергии для тепловых процессов) определяет
количественное соотношение между
изменением внутренней энергии системы
дельта U, количеством теплоты Q, подведенным
к ней, и суммарной работой внешних сил
A, действующих на систему.

Первый
закон термодинамики — Изменение внутренней
энергии системы при ее переходе из
одного состояния в другое равно сумме
количества теплоты, подведенного к
системе извне, и работы внешних сил,
действующих на нее:

Первый
закон термодинамики — количество теплоты,
подведенное к системе, идет на изменение
ее внутренней энергии и на совершение
системой работы над внешними телами:

Частные
случаи первого закона термодинамики
для изопроцессов

При
изохорном процессе объем газа остается
постоянным, поэтому газ не совершает
работу. Изменение внутренней энергии
газа происходит благодаря теплообмену
с окружающими телами:

При
изотермическом процессе количество
теплоты, переданное газу от нагревателя,
полностью расходуется на совершение
работы:

Q=A’

При
изобарном расширении газа подведенное
к нему количество теплоты расходуется
как на увеличение его внутренней энергии
и на совершение работы газом:

Адиабатный
процесс — термодинамический процесс в
теплоизолированной системе.

Адиабатический
процесс.

Адиабатический
процесс — термодинамический процесс
в макроскопической системе, при котором
система не получает и не отдаёт тепловой
энергии.

Для
адиабатического процесса первое начало
термодинамики в силу отсутствия
теплообмена системы со средой имеет
вид: , —
изменение внутренней энергии тела, A —
работа, совершаемая системой

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнение

Первое начало гласит, что общее количество теплоты есть сумма изменения внутренней энергии∆U системы и работы внешних сил А.

Q = ∆U + A.

При отсутствии обмена теплотой выражение будет иметь вид:

∆U + A = 0 или А = − ∆U

Иными словами, в адиабатном термодинамическом процессе работа газа равна убыли его внутренней энергии.

Продолжим преобразования.

Если работа А равна произведению давления p на бесконечно малое изменение объема, то

dU = − pdV

Используя уравнение Менделеева-Клапейрона (МК), запишем для идеального газа:

pdV = − C_vdT.

Откуда следует, что dU = ν C_vdT.

Дифференцирование все части, полная запись преображается следующим образом:

pdV + Vdp = ν RdT,

где R – универсальная газовая постоянная.

Выражаем dT как dU/ν C_v, а dU как – pdV и получаем:

pdV + Vdp = – pdV

Группируем подобные слагаемые:

Vdp = − pdV (1+R/C_v).

Примем сумму (1+R/C_v) за коэффициент γ:

γ = −  

После интегрирования получим запись:

γln V = — ln p + const

Применяя свойства логарифмов, окончательно имеем:

pV^γ = const

Равенство, к которому мы пришли есть уравнение адиабатного процесса. Другое название выражения – уравнение Пуассона. Следует напомнить, что рассматриваемая система – идеальный газ.

В этом уравнении коэффициент γ – показатель адиабаты (коэффициент Пуассона). Его физический смысл – отношение теплоемкостей системы при p = const и V = const, соответственно.

Графическое описание процесса

В координатах «давление – объём» адиабатические явления описываются графиком адиабатой. Кривая напоминает изотерму, но имеет более крутой вид. Это следует из пропорциональности произведения pV температуре T, согласно уравнению МК.

На рисунке кривая 1 является адиабатой, кривая 2 – изотермой для одной и той же идеальной системы.

Исходя из того, что:

pV  T, адиабатный закон можно описать и так: TV^γ−1 = const.

Соотношение между температурой и давлением в адиабатическом процессе:

pT^(γ/1-γ) = const

Как найти работу газа

Чтобы выразить работу А, которую совершает система при Q = 0, снова используем уравнение МК:

dA = − νC_vdT, что после дифференцирования преобразуется так:

А = − νC_v(T₁ – T₂).

Уравнение Мейера для идеальных газов показывает связь между теплоёмкостями при изобарном и изохорном процессах. Согласно этому равенству, разность C_p и С_v есть универсальная газовая постоянная R. Тогда учитывая, что показатель адиабаты – это отношение этих теплоемкостей, выразим С_v в формуле для полной работы:

Подставляем теплоемкость изохорного процесса:

Связь температур, объёмов и давлений в термодинамике идеальных систем выглядит так:

 

Таким образом, работу можно представить через соотношение давлений или объемов:

Примеры задач

1. Температура воспламенения T₂ горючей смеси с показателем адиабаты 1,4 в двигателе Дизеля 1100 К (см. рисунок). Исходная температура Т₁ равна 350 К. Найти, во сколько раз необходимо уменьшить объем смеси сжатием, чтобы произошло воспламенение.

Решение. Воспользуемся соотношением температур и объемов для адиабатного процесса идеального газа. Тогда:

T₁V₁^γ−1 = T₂V₂^γ−1. Выражаем отношение объемов и получаем ответ:

V₁/V₂ = (T₂/T₁)^(1/(γ−1)) = (1100/3500)^2,5 ≈ 17,5 раз.

1. Начальные параметры воздуха Р₁ 0,1 МПа и Т₁ = 300 К. После адиабатного сжатия в компрессоре двигателя давление Р₂ стало 0,28 МПа. После этого при постоянном давлении произошло охлаждение воздушной смеси до 37 °С. Найти работу сжатия и количество отводимой теплоты при охлаждении.

Решение.

Для адиабатического процесса соотношение давлений и температуры:

(Р₂/Р₁)(^γ−1)/γ = Т₂/Т₁, откуда находим температуру по завершении сжатия:

Т₂ = Т₁((Р₂/Р₁)(^γ−1)/γ = 300 (0,28/0,1)^1/0,4 = 402 К.

Показатель адиабаты равен 1,4 для воздуха в данных условиях.

Количество теплоты, которое отводится при изобарном охлаждении равно с учетом перевода градусов Цельсия в Кельвины:

Q = C_p(Т₂ – Т₃) = 1000(402-310) = 92 кДж/кг.

Тогда работа сжатия компрессора равна:

А = R (T₂ – T₁)/γ-1 ≈ 73,2 кДж/кг.

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

к оглавлению ▴

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1).

Рис. 1.

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

(1)

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

к оглавлению ▴

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

к оглавлению ▴

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

(2)

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

(3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

к оглавлению ▴

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

к оглавлению ▴

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Процесс, происходящий без теплообмена с окружающей средой, называется адиабатическим.

Характеристика процесса:

δQ=0δQ = 0.

Применив к адиабатическому процессу первый принцип термодинамики, получим:

δQ+δA=0.δQ+δΑ = 0.

Откуда

δA=−dUδΑ = -dU,

то есть в адиабатическом процессе работа выполняется только благодаря внутренней энергии системы.

Для идеального газа

δA=−СVdt,δΑ=-СVdt,

то есть когда газ выполняет работу против внешних сил в процессе адиабатического расширения, то температура газа снижается. Напротив, в процессе адиабатического сжатия, когда работа выполняется над газом, его температура повышается.

Примеры адиабатических процессов

Очевидно, чтобы исключить теплообмен и осуществить адиабатический процесс, надо было бы термодинамическую систему окружить нетеплопроводной стенкой. В природе таких стенок не существует, но могут создаваться подобные условия, в которых происходят процессы, очень близкие к адиабатическим.

Адиабатические процессы играют важную роль в природе и технике.

То, что в атмосфере верхние слои холоднее от более низких вопреки действию конвекции, а также образование облаков и туманов, можно объяснить, процессами адиабатического расширения воздуха в атмосфере.

Огромные массы воздуха, нагреваясь у поверхности Земли и поднимаясь вверх, попадают в область все более низких давлений и расширяются:

Этот процесс адиабатический, поскольку из-за плохой теплопроводности воздуха теплообменом можно пренебречь. Выполняя работу расширения против внешнего давления, воздух охлаждается, а водяной пар превращается в насыщенный и конденсируется.

Сгущения и разрежения, возникающие в звуковых волнах в газах — это тоже, по сути, процессы адиабатического сжатия и расширения газа. Поскольку звук имеет большую скорость (в воздухе — 340 м / с), процессы здесь происходят так быстро, что за это короткое время теплообменом можно пренебречь.

Все процессы, происходящие очень быстро, приближаются к адиабатическим.

В таких условиях, в частности, осуществляются адиабатические процессы в некоторых тепловых машинах.

Адиабатическое сжатие воздуха и нагрев его вследствие этого хорошо наблюдаются даже в ручных насосах при накачивании велосипедной камеры.

Уравнение Пуассона

В адиабатическом процессе одновременно изменяются все три параметра газа: V,р,Т,V, р, Т, зависимость между которыми выражает уравнение Клапейрона-Менделеева. Дополнительно для адиабатического процесса подтверждается уравнение Пуассона, которое выражает зависимость между давлением и объемом газа в этом процессе. Чтобы найти его, применим к адиабатическому процессу идеального газа первый принцип термодинамики:

0=CVdT+pdV0={{C}_{V}}dT+pdV

Исключив из этого выражения dTdT по уравнению Клапейрона-Менделеева

pV=RT,pV = RT,

то есть

dT=1R(pdV+Vdp)dT=frac{1}{R}(pdV+Vdp)

получим

CVR(pdV+Vdp)+pdV=0frac{{{C}_{V}}}{R}(pdV+Vdp)+pdV=0

Подставив из уравнения Майера R=CP−CVR = CP-CV, поделим числитель и знаменатель дроби перед скобками на CVCV и обозначим CP/CV−γCP/CV — γ.
После этого получим

1γ−1(pdV+Vdp)+pdV=0frac{1}{gamma -1}(pdV+Vdp)+pdV=0

откуда

Vdp+γpdV=0.Vdp + γpdV = 0.

Если почленно разделить это выражение на произведение pV, то получим

dpp+γdVV=0frac{dp}{p}+gamma frac{dV}{V}=0

Проинтегрировав это уравнение, получим

lnp+γlnV=lnС,lnp + γlnV = lnС,

где СС — постоянная интегрирования.

Если пропотенциировать последнее выражение, то получим уравнение Пуассона

pVγ=const,pVγ = const,

где γγ зависит от природы газа (для воздуха γ=1,42γ = 1,42).

Графическое изображение адиабатического процесса

Графически на диаграмме p, V адиабатический процесс изображается кривой, которая называется адиабата:

Поэтому уравнение Пуассона иначе называют уравнением адиабаты. По сравнению с изотермой (пунктир на графике) адиабата является гиперболой высшего порядка, она круче изотермы.

Графически работа газа в адиабатическом процессе определяется площадью подграфика (заштрихованная область на графике) так же, как и в других процессах.

Приведем еще некоторые другие формулы для вычисления работы газа в адиабатическом процессе.

По первому принципу термодинамики для адиабатического процесса идеального газа имеем

dA=−CVdT;dA = -CVdT;

A=CV(T1−T2).A = CV(T1-T2).

Если по уравнению Клайпейрона-Менделеева определить температуру и подставить ее значение в выражение, то получим

A=CVR(p1V1−p2V2)=1γ−1(p1V1−p2V2)A=frac{{{C}_{V}}}{R}({{p}_{1}}{{V}_{1}}-{{p}_{2}}{{V}_{2}})=frac{1}{gamma -1}({{p}_{1}}{{V}_{1}}-{{p}_{2}}{{V}_{2}})

Если проинтегрировать выражение элементарной работы газа, сводя при этом его к одной переменной исключением давления по уравнению Пуассона, то получим

A=∫V1V2pdV=∫V1V2p1V1γdVVγ=p1V1γ−1[1−(V2V1)1−γ]A=intlimits_{{{V}_{1}}}^{{{V}_{2}}}{pdV=}intlimits_{{{V}_{1}}}^{{{V}_{2}}}{frac{{{p}_{1}}{{V}_{1}}^{gamma }dV}{{{V}^{gamma }}}=frac{{{p}_{1}}{{V}_{1}}}{gamma -1}left[ 1-{{left( frac{{{V}_{2}}}{{{V}_{1}}} right)}^{1-gamma }} right]}

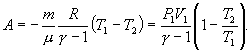
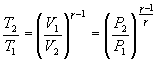
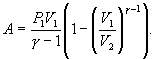
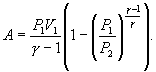
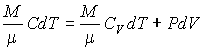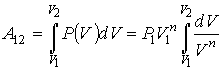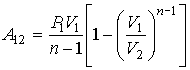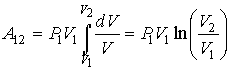
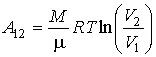Тест по теме «Адиабатический процесс»