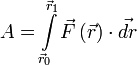Usually, a dancing person is considered to be more energetic compared to a sitting person. A security guard who has been standing at his place the whole day has been working for hours. In real life, this seems obvious, but these terms and definitions work differently when it comes to physics. In physics, work has been defined as the product of force and displacement. This means, that if there is no displacement, work done is zero, no matter how much force or time was spent. This definition builds up concepts like the work-energy theorem. Let’s see this in detail.
Work
Consider a block of mass M sitting on a surface. Now, Aman comes and starts applying a force F, on the block. Only applying the force for some time, he is able to shift the block by 4 meters on the surface. The block and the force are shown in the figure below. Now, since displacement is there. According to physics terminology, the work is done.
For a constant force
and the displacement
. The work done is defined by,
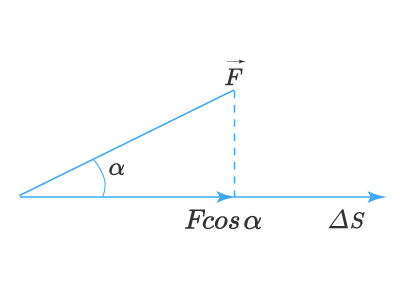
This is the dot product between two vectors, so if the Force makes an angle with the displacement. Then the work done will be given by,
W = |F||r|cos()
Work done by a Variable Force
The above equations are cases of calculating work done with the assumption that the force that is being applied to the body is constant. Often, this is not the case. Forces vary in direction and magnitude with time and sometimes with distance too. So, calculating the work done with this assumption is not right and is not perfectly generalizable.
Let’s consider a force that changes its magnitude. Consider the case of a spring and Hooke’s law. According to Hooke’s law, the restoring force of a perfectly elastic spring is proportional to its extension. The direction of this force is opposite to the extension. There the force acting is given by,
F = -kx
Here, k is the spring constant.
This is an example of a variable Force. For calculating the work done by a variable force, we should add all the infinitely small work done in all the infinitesimally small intervals. Let’s denote the infinitesimally small interval by “dt”. So, to add to the work done in such a scenario, an integral must be used.
The interval “dt” can be used to calculate the change in the extension of spring.
dx = vdt
Using the relations of force from the Hooke’s law.
This work is done by a force applied on the spring for an extension of
For a force which is varying and is given by
and produces a displacement given by the vector
. The work done is given by,
Force-Displacement Plot
The above concept can be understood more clearly using the force-displacement plot. The plot below shows a variable force with the displacement it is producing. It is known that the integrals represent the area under the curve. So, in this case, the area under the curve gives the work done by the force on the body. The area under the curve is divided into many rectangles which represent the displacement.
The area of a single rectangle is . This represents the work done by the force for an infinitesimally small displacement. The total sum of the area of all the rectangles gives the total work done.
W =
⇒ W = ∫Fdx
Sample Problems
Question 1: Find the work done when a force of 20N acting in the direction of displacement produces a displacement of 5 m.
Solution:
The work done by a constant force is given by,
W = |F||r|cos(
)
Here,
W = |F||r|cos(
)
⇒ W = (20)(5)(cos(0))
⇒ W= 100
Question 2: Find the work done when a force of F = 30i + 5j produces a displacement r = 5i + 2j.
Solution:
The work done by a constant force is given by,
W =
and
Calculating the dot product.
W =
⇒ W = (30i + 5j). (5i + 2j)
⇒ W= (30)(5) + (5)(2)
⇒W = 150 + 10
⇒W = 160 J
Question 3: Find the work done when a force of F = x produces a displacement of 4m.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = x
Calculating the work done.
W =
Here, the displacement is x = 4
W =
⇒ W =
⇒ W = 8J
Question 4: Find the work done when a force of F = x2 produces a displacement of 3 m.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = x2
Calculating the work done.
W =
Here, the displacement is x = 3
W =
⇒ W =
⇒ W = 4.5 J
Question 5: Find the work done when a force of F = x + 4 produces a displacement of 2 m.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = x + 4
Calculating the work done.
W =
Here, the displacement is x = 2
W =
⇒ W =
⇒ W = 10 J
Question 6: Find the work done when a force of F = sin(x) produces a displacement from -1 to 1.
Solution:
The work done by a variable force is given by,
W = ∫Fdx
F(x) = sin(x)
Calculating the work done.
W =
Last Updated :
30 Jun, 2021
Like Article
Save Article
Работой силы FF, действующей на материальную точку, называют физическую величину, равную скалярному произведению вектора действующей силы на вектор перемещения точки drdr:
dA=(F⃗dr⃗)=Fdrcos(F⃗,dr⃗^)dA=(vec{F}dvec{r})=Fdrcos(widehat{vec{F},dvec{r}})
Иначе записывают dA=FcosαdsdA=Fcosalpha ds:
Выражают работу в СИ в джоулях. Джоуль – это работа силы в 1 Н на пути в 1 м условии, что направление действия силы и направление перемещения совпадают. В аналитическом виде
1 Дж = 1Н · 1м= 1 (кг·м2)/с2
Нулевая работа
Работа – скалярная величина. В зависимости от угла между направлениями действующей силы и перемещения она может быть положительной, отрицательной и равна нулю. Нулевой будет работа силы, которая перпендикулярна к направлению перемещения, в частности нулевой является работа центростремительных сил, работа силы тяжести во время движения тела в горизонтальной плоскости и др.
В основном, например, во время равномерного подъема тела, работа действующей силы сводится к преодолению силы тяжести. В случае равномерного движения тела на горизонтальной поверхности – к преодолению силы трения, в производственной сфере – к преодолению сопротивления почвы, сопротивления различных материалов при обработке и тому подобное. Поэтому под работой на практике понимают процесс преодоления сопротивления при перемещениях тел.
Работа переменной силы
Выше мы рассмотрели способ вычисления работы постоянной силы при прямолинейном перемещении тела. Работу переменной силы или произведение переменной проекции силы на направление перемещения, также определяют по формуле:
dA=(F⃗dr⃗)=Fdrcos(F⃗,dr⃗^)dA=(vec{F}dvec{r})=Fdrcos(widehat{vec{F},dvec{r}}),
которую можно применить только для бесконечно малого перемещения drdr.
Работу на всем пути найдем как сумму работ на всех элементарных перемещениях, на которые разделены путь. Эта операция сводится к вычислению интеграла:
A=∫SFcosαdsA=intlimits_{S}{Fcosalpha ds}
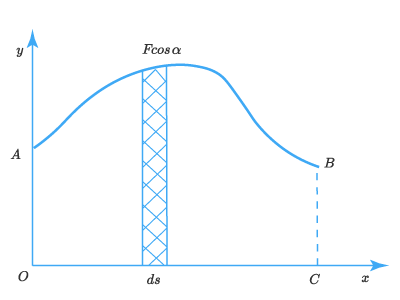
Наряду с аналитическим широко используют графический способ определения работы. Отложив по оси ОуОу проекцию действующей силы FcosаF cos а, а по оси ОхОх – пройденный телом путь ss, получим графическую зависимость между ними в виде кривой АВАВ:
Отсюда следует, что работа при элементарном перемещении
dA=FcosαdsdA=Fcos alpha ds:
равна площади заштрихованной полоски, а работа на всем пути – площади фигуры ОАВС. Например, если вычислить площадь фигуры с помощью индикатора.
Прибор, фиксирующий изменения любого параметра или объекта в форме, удобной для непосредственного восприятия человеком, то можно определить работу газа в цилиндре тепловой машины.
Работа силы тяжести
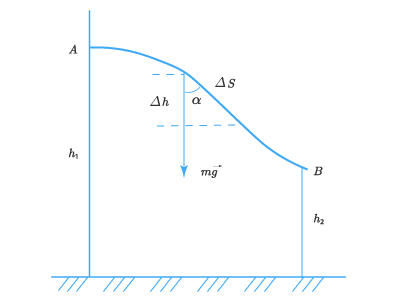
Рассмотрим важный пример работы силы тяжести при движении тела по некоторой кривой АВ:
Поделим весь путь на такие малые части, чтобы их можно было считать прямолинейными. Работа на одной из них:
ΔA=FΔscosα=mgΔscosα=mgΔhDelta A=FDelta scos alpha =mgDelta scos alpha =mgDelta h
Работу на всем пути найдем как сумму работ на отдельных его частях:
A=∑mgΔh=mg∑Δh=mg∑(h1−h2)A=sum{mgDelta h}=mgsum{Delta h}=mgsum{({{h}_{1}}-{{h}_{2}}})
Как видим, работа силы тяжести (или работа против силы тяжести) для тела, которое перемещается в поле тяготения, не зависит от формы траектории, а зависит только от разности высот его начальной и конечной точек приложения.
Если бы тело в поле притяжения описывало замкнутую траекторию, то суммарная работа силы тяжести равнялась бы нулю: положительная работа тела, возникающая в случае, когда оно опускается, компенсируется отрицательной работой тела, когда оно поднимается.
Силы, работа которых не зависит от траектории движения тела, а зависит только от начального и конечного его положений, называются потенциальными.
Таковы, например, силы всемирного тяготения, силы упругости, электростатические силы. Поля, в которых проявляется действие таких сил, называются потенциальными.
Система тел называется консервативной, если в ней внутренние силы взаимодействия потенциальные, а внешние силы, действующие на эти тела, –стационарные и потенциальные.
Тест по теме «Работа силы»
-
Механическая работа. Работа переменной силы.
Механическая
работа —
это физическая
величина,
являющаяся скалярной количественной
мерой действия силы или
сил на тело или систему, зависящая от
численной величины, направления силы
(сил) и от перемещения точки (точек) тела
или системы.
При
прямолинейном движении одной материальной
точки и постоянном значении приложенной
к ней силы работа
(этой силы) равна произведению величины
проекции вектора силы на направление
движения и величины совершённого
перемещения:
Здесь
точкой обозначено скалярное
произведение,
— вектор
перемещения; подразумевается, что
действующая сила
постоянна
в течение всего того времени, за которое
вычисляется работа.
Если
сила не постоянна, то в этом случае она
вычисляется как интеграл:
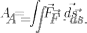
(подразумевается
суммирование по кривой, которая является
пределом ломаной, составленной из
последовательных перемещений
если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
Если
существует зависимость силы от координат,
интеграл определяется следующим образом:
,
где
и
— радиус-векторы начального
и конечного положения тела соответственно.
-
Cледствие:
если направление движения тела
ортогонально силе, работа (этой силы)
равна нулю.
Работа переменной силы
Пусть
материальная точка перемещения под
действием силы F,
которая направлена вдоль оси Ох,
имеет переменную величину, которая
непрерывно зависит от х.
Требуется определить работу А,
совершаемую силой F,
по перемещению материальной точки вдоль
оси Ох из
точки х
= а в
точку х
= b ( а < b).
Функция F(х)
предполагается непрерывной на отрезке
[ а, b].
Разобьем
произвольно отрезок [а, b]
на n частей
точками а = х0 < x1 < x2 <
… < xn = b.
Выберем на каждом частичном отрезке
[x i —
1, xi]
точку ξ i.
Сила, действующая на материальную точку
на отрезке [x i —
1, x i],
изменяется от точки к точке. Но если
длина отрезка мала, то значение силы в
точках отрезка [x i —
1, xi]
мало отличается от ее значения в любой
точке ξ i Î [xi —
1, xi],
так как F (x)
непрерывна. Поэтому работу А i,
совершаемую силой F на
[xi —
1, xi]
можно считать приближенно равной работе
совершаемой на том же отрезке постоянной
силой F(ξ i ),
т. е.
Ai ≈ F (ξi)
Δxi.
Рассуждая
аналогично для каждого отрезка разбиения,
получаем приближенное значение
работы А силы
F на всем отрезке:
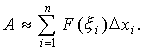
С
другой стороны, сумма в правой части
равенства является интегральной суммой
для функции F (x).
Так как функция F (x )
непрерывна на отрезке [a, b],
то предел этой суммы при
существует
и равен определенному интегралу от
функции F (x )
по отрезку [a, b].
Таким образом,
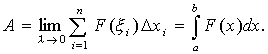
17)
Принцип относительности в классической
и релятивистской механике
классическая:
Принцип
относительности утверждает, что во всех
инерциальных системах все механические
процессы описываются одинаковым образом,
т.е. посредством законов, имеющих ту же
самую математическую форму.
Иначе
говоря, в таких системах законы движения
тел описываются теми же самыми
математическими уравнениями или
формулами.
релятивистская:
В
отличие от классической механики, в
специальной теории относительности
одновременность двух событий, происходящих
в разных точках пространства, относительна:
события, одновременные в одной инерциальной
системе отсчёта, не одновременны в
других инерциальных системах, движущихся
относительно первой.
18)
Энергия. Виды механической энергии
общая
количественная мера движения и
взаимодействия всех видов материи.
Энергия
не возникает из ничего и никуда не
исчезает, она может только переходить
из одного вида в другой.
Понятие
энергии связывает все явления природы
в одно целое, является
общей
характеристикой состояния физических
тел и физических полей
Виды:
механическая
, электромагнитная , химическая , ядерная
,тепловая , гравитационная и др.
!!19)
Основные
понятия и величины динамики вращательного
движения.
Основной
закон динамики вращательного движения
можно получить из второго закона Ньютона
для поступательного движения твердого
тела. Если к твердому телу массой m в
точке А приложить силу F,
то в результате жесткой связи между
всеми материальными точками тела все
они получат угловое ускорение
и
соответственные линейные ускорения,
как если бы на каждую точку действовала
сила
.
Для каждой материальной точки.
,
где
–
момент силы – это произведение силы
на
ее плечо
.
Плечом
силы называют кратчайшее расстояние
от оси вращения “ОО” до линии действия
силы
.
20)
Консервативные
и неконсервативные силы и системы
консервативная:
Силы, работа которых не зависит от формы
траектории, а определяется только
начальным и конечным размещением тела
в пространстве.
—
силы притяжения
—
силы упругости
—
электростатические силы взаимодействия
между заряженными телами
неконсервативные:
Эти силы зависят не только от формы
тел, но и от их скорости. Они направлены
всегда против направления скорости,
потому работа сил трения всегда
отрицательна.
—
силы трения, которые возникают при
скольжении одного тела по поверхности
другого
—
силы сопротивления, которых испытывает
тело, двигаясь в жидкой или газообразной
среде
!!21)
Кинетическая
энергия релятивистской частицы
частица,
движущаяся с релятивистской скоростью,
то есть скоростью, сравнимой со скоростью
света. Движение таких частиц, рассматриваемых
как классические (неквантовые) материальные
точки, описывается специальной теорией
относительности. Безмассовые частицы
фотоны всегда являются релятивистскими,
поскольку могут существовать, лишь
двигаясь со скоростью света.
22)
Связь
между механической работой и энергией.
То
тело, которое способно совершать работу,
обладает энергией.
Механическая
энергия идет на производство работы и
плюс потери на нагревание окружающей
среды
23)
Момент
силы относительно точки и относительно
оси
Момент
силы относительно точки О — это вектор,
модуль которого равен произведению
модуля силы на плечо — кратчайшее
расстояние от точки О до линии действия
силы. Направление вектора момента силы
перпендикулярно плоскости, проходящей
через точку и линию действия силы, так,
что глядя по направлению вектора момента,
вращение, совершаемое силой вокруг
точки О, происходит по часовой стрелке
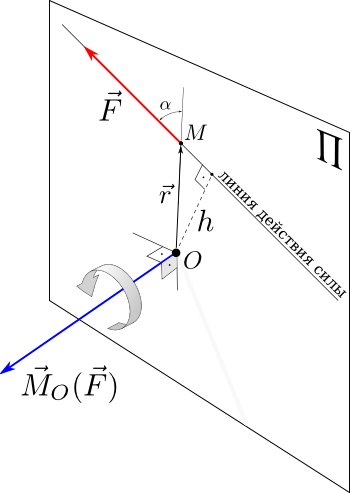
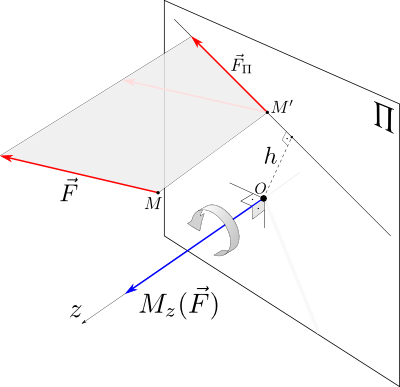
Момент
силы относительно оси вычисляется как
момент проекции силы F⃗ на плоскость
Π, перпендикулярную оси, относительно
точки пересечения оси с плоскостью.
Знак момента определяется направлением
вращения, которое стремится придать
телу сила F⃗ Π. Если, глядя по направлению
оси Oz сила вращает тело по часовой
стрелке, то момент берется со знаком
«плюс», иначе — «минус».
24)
Момент
инерции частицы и твёрдого тела
относительно оси. Теорема Штейнера.
Теорема
Штейнера. момент
инерции тела
относительно
произвольной оси равен сумме момента
инерции этого тела
относительно
параллельной ей оси, проходящей через
центр масс тела, и произведения массы
тела
на
квадрат расстояния
между
осями:
где
—
известный
момент инерции относительно оси,
проходящей через центр масс тела,
—
искомый
момент инерции относительно параллельной
оси,
—
масса
тела,
—
расстояние
между указанными осями.
25)
Момент
импульса относительно точки и относительно
оси.
называется
физическая величина, определяемая
векторным произведением:
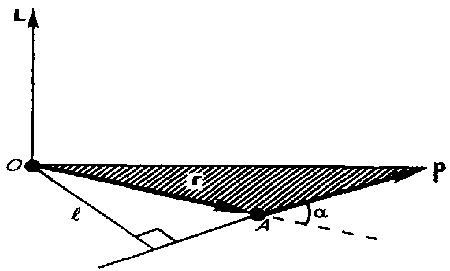
где
r — радиус-вектор, проведенный из точки
О в точку A, p=mv — импульс материальной
точки, L — направление которого совпадает
с направлением поступательного движения
правого винта при его вращении от r к р.
называется
скалярная величина, равная проекции на
эту ось вектора момента импульса,
определенного относительно произвольной
точки О данной оси.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
27.03.2015140.8 Кб71.doc
- #
27.03.2015421.24 Кб871.docx
- #
27.03.20154.73 Mб5771.rtf
- #
Обновлено: 29.05.2023
Сила меняется по каким то своим параметрам. Ну и значит надо найти работу этой силы и всего то.
Как известно, работа силы на пути S равна:
A = F*S
Но эта формула имеет смысл лишь если вдоль всего пути S силя является постоянной величиной.
Если сила меняется от точки к точке на всем пути, то она является функцией пути:
F = F(s)
Тогда разбиваем путь S на очень малые промежутки ds так, что можно считать, что сила F на каждом промежутке пути постоянна. В таком случае можно считать, что на каждом i-том промежутке работа равна:
Ai = F(si)ds
где si — некоторая точка внутри промежутка.
Т. к. работа — величина аддитивная, то чтобы найти работу на всем пути, надо просуммировать все Ai.
Если в сумме устремить ds к нулю то переходим к интегралу:
A = Integral_F(s)ds
где Integral — это знак интеграла. Интегрировать надо от начальной до конечной точки пути.
Тела, образующие механические системы, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, подразделяются на внутренние и внешние. Внутренние силы — это силы, с которыми на данное тело воздействуют остальные тела системы. Внешние силы — это силы, обусловленные воздействием тел, не принадлежащих данной системе. В случае, если внешние силы отсутствуют, система называется замкнутой. Кинетическая энергия. Если система замкнута, то есть =0, то , а сама величина остаётся постоянной. Кинетическая энергия связана с работой внешних и внутренних сил. Если на частицу действует сила , кинетическая энергия не остаётся постоянной. В этом случае, согласно утверждению , приращение кинетической энергии за время dt равно скалярному произведению dS (dS — перемещение частицы за время dt). Величина называется работой силы F на пути dS (dS — это модуль перемещения). Работа результирующей всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы, , следовательно, энергия имеет такую же размерность, как и работа, в соответствии энергия измеряется в тех же единицах, что и работа. Понятие поля. Консервативные силы и потенциальные поля. Потенциальная энергия материальной точки во внешнем силовом поле. Связь силы и потенциальной энергии. Поле центральных сил. Потенциальная энергия системы. Потенциальная энергия упругой деформации. Потенциальная энергия в поле тяготения. Поле сил — это поле, в котором частица в каждой точке пространства подвержена воздействию других тел. Для стационарного поля может оказаться, что работа, совершаемая над частицей силами поля, зависит лишь от начального и конечного положения частицы и не зависит от пути, по которому двигалась частица. Силы, обладающие таким свойством, называются консервативными силами. Отметим, что консервативное поле сил являются частным случаем потенциального силового поля. Поле сил называется потенциальным, если его можно описать функцией П (x,y,z,t), градиент которой определяет силу в каждой точке поля: F= П.ФункцияП называется потенциальной функциейили потенциалом. — это величина для частицы, находящейся в поле консервативных сил Þ U входит слагаемым в интеграл движения имеющей размерность энергии. В связи с этим функцию U(x,y,z) называют потенциальной энергией частицы во внешнем поле сил. Иначе можно сказать, что работа совершается за счет запаса потенциальной энергии. Связь силы и потенциальной энергии существует. (перевернутый треугольник это оператор набла) – Сила это минус градиент потенциальной энергии. Поле центральных сил — это поле, характерное тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр, а величина силы зависит только от расстояния до этого центра F=F(r). Согласно , полная механическая энергия системы независимо действующих частиц, на которые действуют только консервативные силы, остаётся постоянной. Это утверждение выражает закон сохранения энергии для указанной механической системы. Согласно формуле как для расширения, так и для сжатия пружины на величину x, необходимо затратить работу . Эта работа идет на увеличение потенциальной энергии пружины. Зависимость потенциальной энергии пружины от удлинения имеет вид где k-коэффициент жесткости пружины (эта формула написана в предположении, что потенциальная энергия недеформированной пружины равна нулю). При упругой продольной деформации стержня совершается работа, определяемая формулой A=1/2(Es/l0)(Dl)2=1/2Esl0(Dl/l0)2=1/2Eve2. В соответствии с этим, потенциальная энергия упруго деформируемого стержня равна , где e — относительная деформация , E — модуль Юнга, а V — это объём тела. Потенциальная энергия в поле тяготения.
Лекция 4. Работа и энергия
План лекции
4.1. Работа переменной силы. Мощность.
4.2. Энергия. Кинетическая и потенциальная энергии.
4.3. Закон сохранения энергии в механике.
Работа переменной силы. Мощность.
Если под действием силы F происходит движение и тело перемещается на величину S, то говорят, что сила совершает работу. Работа – скалярная физическая величина, равная произведению проекции силы Fs на направление перемещения на перемещение S.
Эта формула справедлива для прямолинейного движения при Fs= const, а также когда угол между вектором силы и перемещением не изменяется. Учитывая, что Fs = F·cos выражению (4.1) можно придать вид:
А = F · S cos (4.2)
Другими словами, работу можно представить как скалярное произведение векторов и .
А = · (4.3)
Из формулы (4.2) видно, что работа может иметь как положительное, так и отрицательное значение. Когда cos >0 (a – острый угол), работа положительна (А>0), при cos
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.004)
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:
где F — сила, действующая на тело, — перемещение, α — угол между силой и перемещением.
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов F и .
2 Смотреть ответы Добавь ответ +10 баллов
Ответы 2
1) Механи́ческая рабо́та — это физическая величина — скалярная количественная мера действия силы на тело или сил на систему тел. Зависит от численной величины и направления силы и от перемещения тела
2)Если направления движения тела и действующей на него силы совпадают, то работа такой силы положительна. Если же направления силы и движения тела противоположны, то работа силы отрицательна. Работа силы равна нулю, если перемещение тела в направлении действия этой силы равно нулю.
3) Если требуется рассчитать работу силы, изменяющейся с течением времени, то перемещение материальной точки разбирают на достаточно малые перемещения, чтобы на каждом из этих перемещений модуль силы и угол между векторами силы и перемещения можно было считать постоянными. После этого вычисляют работу на каждом из этих перемещений и находят сумму работ.
4) Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот.
6) В классической механике перемещение и сила не зависят oт выбора системы отсчёта, значит и работа силы тоже не зависит от выбора системы отсчёта.
Читайте также:
- Стволовые клетки план урока
- Как происходит вторичное засоление и заболачивание почв кратко
- Анализ стихотворения предчувствую тебя года проходят мимо блок по плану кратко
- Какие бывают школы дополнительного образования
- Нужно ли учителю самостоятельно проводить в школе научно педагогические исследования
сила тяги=m*a
находим ускорение а=30/20
сила тяги=ma+коэфициент трения*m*g
cила тяги=1000*3+0,05*1000*20=4000
Ответ: с) 2.1 * 10^-5 м^3
Q=Еп
cm∆t=mgh | ÷m
c∆t = gh
∆t = (gh)/c
∆t = (10×50)/140 ~ 3.571°С
Ответ a)
потому что гальванопластика это изготовление рельефных изделий с помощью электролиза
1 Выражаем дальность полета S=Vo*cos a*t
2 Находим максимальную высоту h= (Vo*sin a)^2/2*g
3 Приравниваем с учетом того то S=4*h
4 Находим все время полета t= 2*Vo*sin a/g
5 Подставляем t в уравнение 3
Решаем должно получиться tg a= 18 ???????? ВЫЧИСЛИ САМ



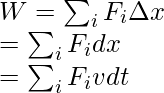
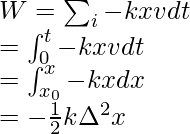

![Rendered by QuickLaTeX.com int^{x}_{0}Fdx \ = int^{x}_{0}xdx \ = [frac{x^2}{2}]^{x}_{0} \ = frac{x^2}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65c5f8e518dfcc356aad74d2e4673f1a_l3.png)
![Rendered by QuickLaTeX.com int^{x}_{0}Fdx \ = int^{x}_{0}x^2dx \ = [frac{x^3}{3}]^{x}_{0} \ = frac{x^3}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65cb36228b7aef5e7e5f12a7cb7b741d_l3.png)
![Rendered by QuickLaTeX.com int^{x}_{0}Fdx \ = int^{x}_{0}(x + 4)dx \ = [frac{x^2}{2} + 4x]^{x}_{0} \ = frac{x^2}{2} + 4x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54540c8109188a35b5be07b5a95c71ec_l3.png)
![Rendered by QuickLaTeX.com int^{1}_{-1}Fdx \ = int^{1}_{-1}sin(x)dx \ = [-cos(x)]^{1}_{-1} \ = cos(-1) - cos(1) \ = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1057a8e06af8309fce2bd667940245fa_l3.png)