Работа против силы тяжести, формула
Возле поверхности Земли, от самой поверхности до небольшой высоты можно пренебречь изменением ускорения свободного падения в зависимости от высоты и считать эту величину постоянной:
[
g = 9.81 (м/c^2)
]
Если тело равномерно поднимается, т.е. движется с постоянной скоростью в направлении, противоположном направлению действия силы тяжести, то согласно общей формуле работы, над телом совершается работа
W = Fs, где F — сила; она совпадает по направлению с перемещением s и равна по величине весу тела G = mg.
[
W = Fs
]
[
F = G = mg
]
[
W = mgs = mgh
]
Здесь:
W — работа по поднятию тела (Дж),
G — вес тела, сила тяжести (Ньютон),
g — ускорение свободного падения, 9.81 (м/с²),
s=h — высота на которую поднимают тело (метр),
m — масса тела (кг)
Вычислить, найти работу против силы тяжести по формуле (3)
Работа против силы тяжести |
стр. 464 |
|---|
- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что работа подъема тела в однородном поле тяжести всегда больше величины потенциальной энергии mgh. Величина работы имеет минимум, величина которого зависит от способа подъема тела.
В школьных [1] и вузовских [2-4] курсах физики утверждается, что если тело массы m равномерно поднимать вверх на высоту h с помощью силы F=mg, то сила совершает положительную работу AF=mgh, равную потенциальной энергии П=mgh, а сила тяжести отрицательную работуAP=-mgh [1]. Рассматривается также случай бросания тела вертикально вверх с начальной скоростью V0, обеспечивающей подъем тела на высоту h на основании закона сохранения и превращения энергии: K=П или . Работу бросания считают равной
. В этих безобидных, на первый взгляд, утверждениях, содержится нечто, противоречащее одному из положений физики. В физике используется понятие КОЭФФИЦИЕНТА ПОЛЕЗНОГО ДЕЙСТВИЯ (η ) — КПД. КПД не может быть больше единицы. КПД всегда меньше единицы, поскольку часть энергии превращается тоже в энергию, но не в ту, что нужна, и поэтому теряется для полезного использования. КПД всегда меньше единицы вследствие самой физической природы вещей и явлений. Если же записать КПД для выше приведенных случаев подъема тела на высоту h, то получим:
. Рассмотрим более подробно ряд случаев подъема тела на высоту h.
§ 1. Рассмотрим движение тела, брошенного вертикально вверх с начальной скоростью V0, за счет действия мгновенной силы в виде 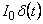
— δ- функция Дирака [7, 8]. Величину I0 будем называть единичным импульсом силы, численно равным количеству движения (импульсу), полученным телом I0=mV0. Дифференциальное уравнение движения (II закон Ньютона) имеет вид:
(1)
при нулевых начальных условиях:
;
(2)
Где x— вертикальная координата, отсчитываемая от поверхности Земли. Для решения задачи воспользуемся двусторонним преобразованием Лапласа [9]
(3)
Для решения этой задачи используется дифференциальное уравнение для односторонней функции где H(t) — единичная (ступенчатая) функция Хевисайда [8, 9]. Тогда производные функции x*(t) имеют вид [9]
;
После соответствующих преобразований, решение получается в следующем виде
(4)
Вычислим работу, совершаемую силами
(5)
Вычисляя интегралы, получим [9]
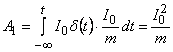
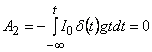
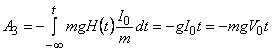
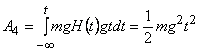
Работа, совершаемая силами, запишется в виде:
(6)
Работа, совершенная единичным импульсом силы I0=mV0 (или начальная энергия, полученная телом) будет равна
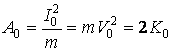
где — начальная кинетическая энергия тела. Время подъема до максимальной высоты
, а максимальная высота подъема
. Подставляя в выражение (6) значение t0, получим конечное значение совершенной работы:
(8)
Поскольку начальная энергия полученная телом A0=2K0, то КПД процесса бросания тела вертикально вверх будет равен
То, что начальная энергия тела A0=2K0 можно объяснить эффектом удвоения массы (силы тяжести) в случае внезапно приложенной нагрузки при бросании [5, 10].
§ 2. Рассмотрим случай движения тела вертикально вверх под действием постоянной вертикальной силы тяги FT. Уравнение движения (II закон Ньютона) запишется в следующем виде
(9)
Если FT=mg, то правая часть тождественно равна нулю, и движения тела вверх не происходит, но в этом случае сила давления тела на опору (например, на поверхность Земли) равна нулю, поскольку сила тяги нейтрализует «тяжелую» массу, и тело находится в квазиневесомом состоянии (состояние левитации). Обозначим силу тяги, равную mg, значком «Л»: FЛ=mg. Если сила тяги больше mg на величину ΔF, то уравнение (9) можно переписать в виде
или
(10)
Таким образом, часть силы тяги FЛ =mg не будет принимать непосредственного участия в работе по подъему тела вверх. Тело будет подниматься вверх только благодаря действию силы ΔF с ускорением . За время t высота подъема будет равна
(11)
Работа подъема составит величину, равную
(12)
Поскольку есть импульс силы, численно равный импульсу (количеству движения), полученному телом
, где V1 — скорость тела в момент времени t, то можно записать
.
Однако чтобы остановить тело на данной высоте h, необходимо еще совершить работу торможения, численно равную кинетической энергии, приобретенной телом ;
(13)
Отдельного разговора заслуживает вопрос о том, что же делает другая часть силы тяги FЛ=mg? Ведь она не принимает участия в подъеме тела на высоту h, она лишь нейтрализует силу тяжести, обеспечивая условия левитации. Можно записать баланс импульсов сил в виде:
(14)
Возведя обе части равенства в квадрат и разделив на 2m, получим баланс энергий (работ):
(15)
Работу, совершаемую силой FT, можно переписать в следующем виде:
(16)
Или, с учетом выражений (11) и (12):
(17)
Первый член в правых частях выражений (15)-(17) представляет собой работу силы левитации в стационарном (неподвижном) состоянии
(18)
Второй член выражает работу, связанную с ускоренным перемещением силы левитации
(19)
Третий член — это обычная работа силы ΔF, обеспечивающей ускоренное движение тела в соответствии со II законом Ньютона:
(20)
Произведение работ . На рис. 1 показана зависимость величины работы левитации AЛ от величины работы AΔ, выраженных в долях потенциальной энергии mgh.
Выражение (17) имеет минимум, равный при
. На графике (рис. 2) показана зависимость работы
, совершаемой силой тяги FT, выраженной в долях потенциальной энергии П=mgh, от величины соотношения ΔF / mg. Если использовать обычную формулу определения работы подъема тела на высоту h с некоторым ускорением a, то будем иметь A=m(g+a)h = (FЛ + ΔF)h . Ее зависимость от величины соотношения ΔF / mg показана на графике (рис. 3). Самое нелепое на этом графике то, что при ΔF=0 совершается работа подъема, равная mgh, хотя, согласно условиям статики, тело должно оставаться неподвижным.
Отрицательная работа, совершаемая силой тяжести при подъеме тела вверх вовсе не равна mgh. Она равна
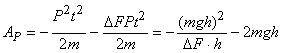
Сумма работ (17) и (21) дает величину , т.е. величину кинетической энергии, приобретенной телом на высоте h.
КПД подъема при без учета работы торможения составляет
.
§3. Тело находится в состоянии левитации (приложена сила тяги ). Для того, чтобы тело двигалось вверх, в начальный момент времени на тело действует направленный вверх единичный импульс силы
. В этом случае дифференциальное уравнение движения запишется в виде
(22)
при нулевых начальных условиях. Решая уравнение с помощью преобразования Лапласа, получим
(23)
Вычисляем работу, совершаемую всеми силами

где , а t1 — время движения до высоты
. Вычисляя интегралы, выделим положительную и отрицательную работы
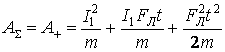
(26)
Преобразуем выражения, входящие в (25)
, где
Тогда суммарную положительную работу (работу подъема) можно записать в виде
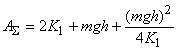
Эта работа имеет минимум, равный при величине
. График зависимости суммарной работы подъема AΣ в зависимости от величины 2K1, выраженных в долях потенциальной энергии П=mgh, показана на графике (рис. 4). Отрицательная работа, совершаемая силой тяжести (27), может быть представлена в виде:
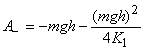
При больших значениях начального импульса ( ) она асимптотически стремится к своему обычному значению
.
Величина энергии, приобретенной в результате ударного нагружения мгновенным импульсом силы I1=mV1, равна . Двойная энергия является результатом удвоения массы при внезапно приложенной нагрузке (в рамках модели материальной точки). В рамках реального упругого тела половина энергии идет на возбуждение упругих колебаний, которые вследствие дисперсии и внутреннего трения с течением времени затухают, переходя во внутреннюю энергию (тело нагревается).
СПИСОК ЛИТЕРАТУР
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. средн. шк. — М.: Просвещение, 1990.
- Сивухин Д.В. Общий курс физики. Том I. Механика. — М.: Наука, 1989.
- Детлаф А.А., Яворский Б.М. Курс физики. Учебн. пособие для вузов. — М.: Высш. шк., 1989.
- Матвеев А.Н. Механика и теория относительности: Учебн. пособие для физ. спец. вузов. — М.: Высш. шк., 1986.
- Иванов Е.М. Дополнительные главы классической механики: — Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических //Успехи современного естествознания, № 9, 2004.
- Арсенин В.Я. Математическая физика. — М.: Наука, 1966.
- Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970.
- Б. Ван Дер Поль, Х. Бреммер. Операционное исчисление на основе двустороннего преобразования Лапласа. — М.: Изд. Иностр.Лит. 1952.
- Иванов Е.М. Закон инерции Галилея (I закон Ньютона) //Вестник ДИТУД, № 1, 2003.
Библиографическая ссылка
Иванов Е.М. РАБОТА ПОДЪЕМА ТЕЛА В ОДНОРОДНОМ ПОЛЕ ТЯЖЕСТИ // Современные наукоемкие технологии. – 2005. – № 3.
– С. 9-12;
URL: https://top-technologies.ru/ru/article/view?id=22372 (дата обращения: 26.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Работа силы тяжести. Потенциальная энергия тела, поднятого над землей
Вертикальное движение тела под действием силы тяжести
При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна , где m – масса тела, g – ускорение свободного падения.
Пусть тело массой m свободно падает с высоты 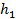
Рис. 1. Свободное падение тела с высоты 
При этом модуль перемещения тела равен разности этих высот:
Так как направление перемещения и силы тяжести совпадают, то работа силы тяжести равна:
Значение высот в этой формуле можно отсчитывать от любого уровня (уровень моря, уровень дна ямы, которая вырыта в земле, поверхность стола, поверхность пола и т. д.). В любом случае высоту данной поверхности выбирают равной нулю, поэтому уровень данной высоты называют нулевым уровнем.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести будет равна:
Если тело, брошенное вверх с нулевого уровня, достигает высоты hнад этим уровнем, то работа силы тяжести будет равна:
Движение тела по прямолинейной траектории, наклонённой под некоторым углом к горизонту
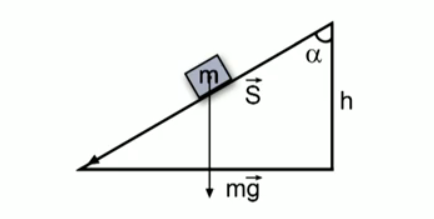
Пусть тело массой m движется по наклонной плоскости высотой h и при этом совершает перемещение , модуль которого равен длине наклонной плоскости (см. Рис. 2).
Рис. 2. Движение тела по наклонной плоскости
Работа силы равна скалярному произведению вектора силы на вектор перемещения тела, совершённого под действием данной силы, то есть работа сила тяжести в данном случае будет равна:
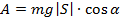
где – угол между векторами силы тяжести и перемещения.
На рисунке 2 видно, что перемещение () представляет собой гипотенузу прямоугольного треугольника, а высота h – катет. Согласно свойству прямоугольного треугольника:
Следовательно
Работа силы тяжести при движении тела по криволинейной траектории
Мы получили выражение для работы силы тяжести такое же, как в случае вертикального движения тела. Можно сделать вывод: если траектория тела не является прямолинейной и тело движется под действием силы тяжести, то работа силы тяжести определяется только изменением высоты тела над некоторым нулевым уровнем и не зависит от траектории движения тела.
Рис. 3. Движение тела по криволинейной траектории
Докажем предыдущее утверждение. Пусть тело движется по некоторой криволинейной траектории (см. Рис. 3). Эту траекторию мысленно разбиваем на ряд малых участков, каждый из которых можно считать маленькой наклонной плоскостью. Движение тела по всей траектории можно представить как движение по множеству наклонных плоскостей. Работа силы тяжести на каждом из участков будет равна произведению силы тяжести на высоту данного участка. Если изменения высот на отдельных участках равны , то работы силы тяжести на них равны:
Полная работа на всей траектории равна сумме работ на отдельных участках:
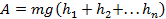
Так как
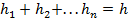
То
Таким образом, работа силы тяжести не зависит от траектории движения тела и всегда равна произведению силы тяжести на разность высот в исходном и конечном положениях. Что и требовалось доказать.
При движении вниз работа положительна, при движении вверх – отрицательна.
Работа силы тяжести при движении тела по замкнутой траектории
Пусть некоторое тело совершило движение по замкнутой траектории, то есть оно сначала спустилось вниз, а потом по какой-то другой траектории вернулось в исходную точку. Так как тело оказалось в той же самой точке, в которой оно было изначально, то разность высот между начальным и конечным положением тела равна нулю, поэтому и работа силы тяжести будет равна нулю. Следовательно, работа силы тяжести при движении тела по замкнутой траектории равна нулю.
Потенциальная энергия тела
В формуле для работы силы тяжести вынесем (-1) за скобку:
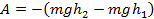
Из прошлых уроков известно, что работа сил, приложенных к телу, равна разности между конечным и начальным значением кинетической энергии тела. В полученной формуле 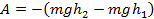
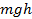
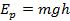
Изменение потенциальной энергии отрицательно по величине, если совершается положительная работа силы тяжести (видно из формулы 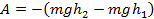
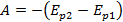
Если тело падает с высоты h на нулевой уровень, то работа силы тяжести будет равна значению потенциальной энергии тела, поднятого на высоту h.
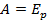
Потенциальная энергия тела, поднятого на некоторую высоту над нулевым уровнем, равна работе, которую совершит сила тяжести при падении данного тела с данной высоты на нулевой уровень.
В отличие от кинетической энергии, которая зависит от скорости тела, потенциальная энергия может быть не равной нулю даже у покоящихся тел.
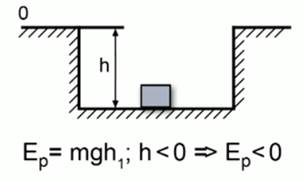
Рис. 4. Тело, находящееся ниже нулевого уровня
Если тело находится ниже нулевого уровня, то оно обладает отрицательной потенциальной энергией (см. Рис. 4). То есть знак и модуль потенциальной энергии зависят от выбора нулевого уровня. Работа, которая совершается при перемещении тела, от выбора нулевого уровня не зависит.
Термин «потенциальная энергия» применяется только по отношению к системе тел. Во всех вышеприведенных рассуждениях этой системой была «Земля – тело, поднятое над Землёй».
Задача (нахождение потенциальной энергии)
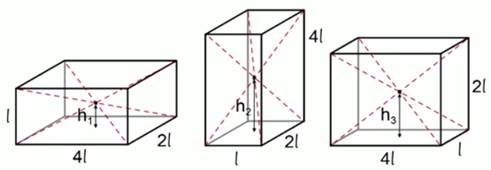
Однородный прямоугольный параллелепипед массой m с рёбрами 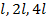
Дано:m – масса параллелепипеда; 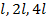
Найти: ;
;
Решение
Если нужно определить потенциальную энергию тела конечных размеров, то можно считать, что вся масса такого тела сосредоточена в одной точке, которая называется центром масс данного тела.
В случае симметричных геометрических тел центр масс совпадает с геометрическим центром, то есть (для данной задачи) с точкой пересечения диагоналей параллелепипеда. Таким образом, необходимо посчитать высоту, на которой расположена данная точка при различных расположениях параллелепипеда (см. Рис. 5).
Рис. 5. Иллюстрация к задаче
Для того чтобы найти потенциальную энергию, необходимо полученные значения высоты умножить на массу параллелепипеда и ускорение свободного падения.
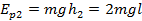
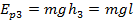
Ответ:;
Совсем недавно, мы
изучили работу силы. Напомним, что работа силы равна произведению модуля силы,
модуля перемещения и косинуса угла между направлениями силы и перемещения:
Рассмотрим теперь частный
случай — работу силы тяжести при перемещении тела с высоты h1
на высоту h2.
Первый случай — это
падение тела вертикально вниз.
В этом случае,
перемещение, конечно же, будет равно
Сила тяжести, как мы
знаем, равна
.
Поскольку сила тяжести
направлена вертикально вниз, как и перемещение, косинус угла между
направлениями этих векторов равен единице. Таким образом, мы получим, что
работа силы тяжести равна:
Второй случай — это когда
тело, наоборот, подбрасывают вертикально вверх с высоты h1
на высоту h2.
В этом случае, угол между
направлением силы тяжести и направлением перемещения составит 180о.
Это приводит нас к тому, что работа силы тяжести опять-таки равна:
Наконец, рассмотрим
случай, когда между направлением силы тяжести и перемещением существует
произвольный угол α.
Обозначим модуль
перемещения за s. В этом случае,
работа силы тяжести равна:
Но, исходя из определения
косинуса:
Таким образом, мы в
третий раз получили одинаковый результат.
Более того, если даже мы
рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.
Любую кривую мы можем
представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и
вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет
равна нулю, поскольку в этом случае направление перемещения перпендикулярно
направлению силы тяжести. На вертикальных участках работа будет равна: A
= mg(s1
+ … + sn).
Очевидно, что эта сумма будет равна (h1
– h2):
Таким образом, мы
убедились, что работа силы тяжести не зависит от траектории движения тела.
Имеет значение лишь то, насколько начальное положение тела отличается от
конечного. Это плавно подводит нас к понятию потенциальной энергии, которое
мы рассмотрим немного позже.
Из приведенных примеров
вытекает еще один важный вывод: при движении тела по замкнутой траектории
работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму
прямоугольника. Как мы уже убедились, при движении тела в горизонтальном
направлении, работа силы тяжести равна нулю. Вектор перемещения направлен
перпендикулярно вектору силы тяжести. При перемещении же по противолежащим
вертикальным сторонам контура, сила тяжести совершает работу, равную по
абсолютной величине, но противоположную по знаку.
В одном случае вектор
перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в
противоположную сторону. Это довольно логично, поскольку при движении тела
вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.
Мы можем сколь угодно
усложнить эту траекторию, получив совершенно произвольный замкнутый контур.
Но опять же, разбив все
кривые на ломаные линии с горизонтальными и вертикальными участками, мы
убедимся, что суммарная работа будет равна нулю.
Силы, обладающие такими
свойствами, называются консервативными. То есть, консервативная сила — это
такая сила, работа которой в замкнутом контуре равна нулю.
Примеры решения задач.
Задача 1. Охотник
стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы
тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы,
то какова её масса?
Задача 2. Находясь
на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом
перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна
5 кг, то каково ускорение свободного падения на Нептуне?
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
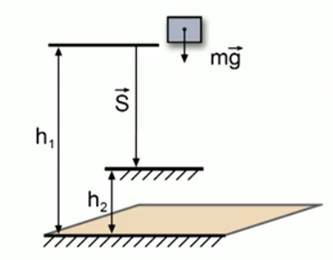
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
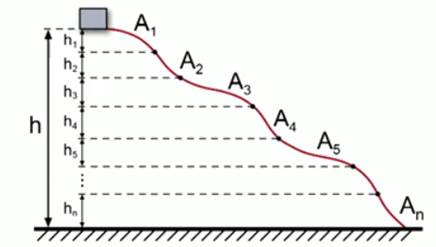
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности