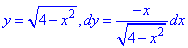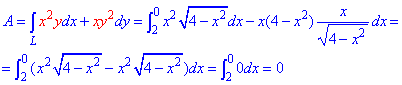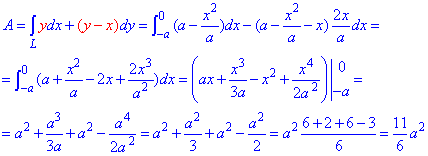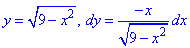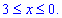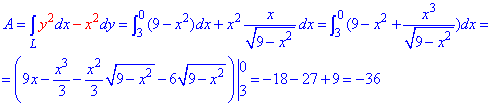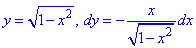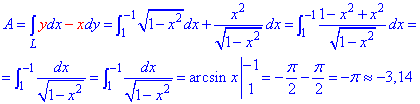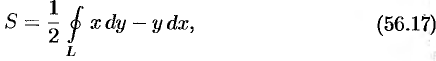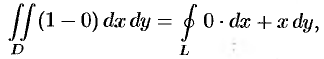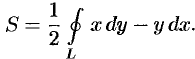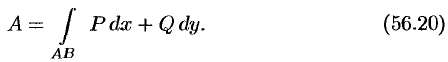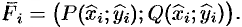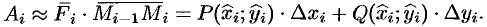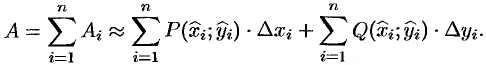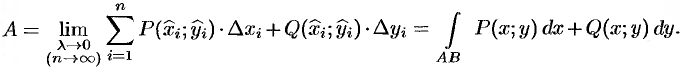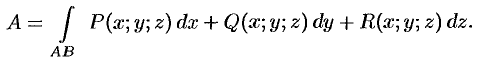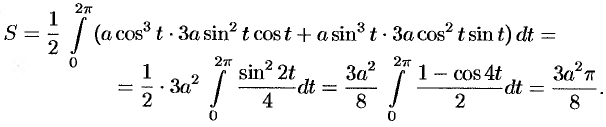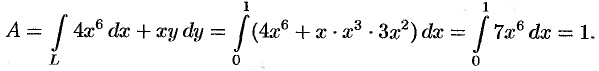Вычисление работы силового поля по перемещению материальной точки не обходится без применения криволинейного интеграла ІІ рода. Чтобы не повторять в каждой новой статье для криволинейных интегралов те же формулы сразу переходим к анализу готовых примеров.
Вычисление работы силового поля с помощью криволинейного интегралу ІІ рода
ЗАДАНИЕ 3.5 Вычислить работу силового поля 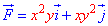
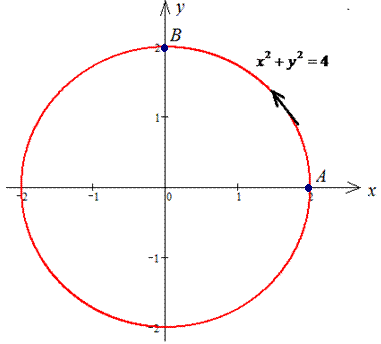
x2+y2=4 от точки A(2;0) к точке B(0;2).
Решение: Построим в декартовых координатах траекторию материальной точки вдоль круга L: x2+y2=4.
Уравнение верхней части полукруга и ее производной равны
В соответствии с точками A(2;0), B(0;2) пределы интегрирования изменяются от 2 до 0.
Не удивляйтесь, что не в обратном порядке. Их всегда нужно выписывать в порядке обхода контуру от точки A к B.
Робота силового поля F по перемещения материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
Внимательно пересмотрите уравнение силового поля и подинтегральную функцию и Вам станет понятно, что и откуда берется. Как вычислить криволинейный интеграл детально расписано в предыдущих статьях (меняем y, dy на ф-и от «х» под интегралом).
ЗАДАНИЕ 3.10 Найти работу силового поля 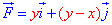
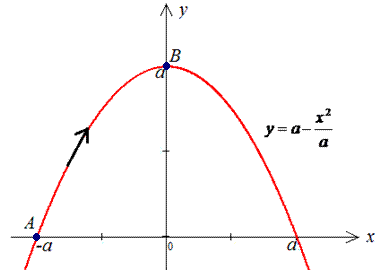
y=a-x2/a от точки A(-a;0) к точке B(0;a).
Решение: Имеем y=a-x2/a — уравнение параболы, находим дифференциал dy=-2x/a*dx и пределы изменения переменной
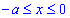
Вычисляем работу силового поля F, потраченную на перемещению материальной точки вдоль вдоль линии L
Криволинейный интеграл ІІ рода находим за первой формулой интегрирования.
ЗАДАНИЕ 3.12 Вычислить работу силового поля 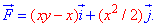
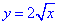
Решение: Строим траекторию материальной точки вдоль корневой функции L: 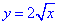
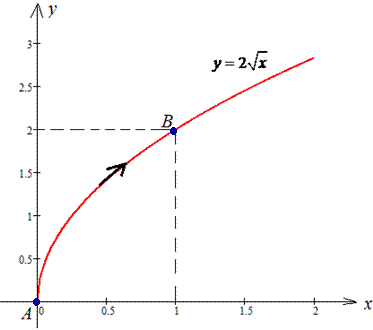
Записываем производную 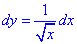
Находим роботу A силового поля F : 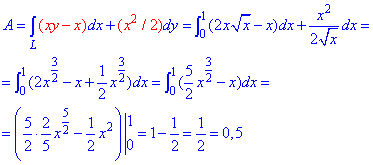
Перед интегрированием превращаем корни к показательной форме записи, а дальше вычисляем за табличными формулами интеграл.
ЗАДАНИЕ 3.14 Вычислить работу силового поля 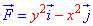
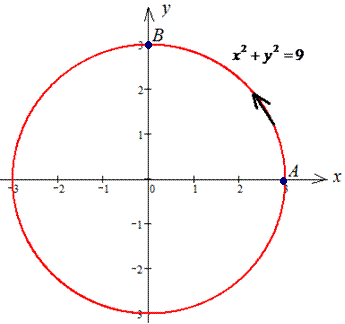
x2+y2=9.
Решение: Наведем траекторию движения материальной точки по кругу L: x2+y2=9.
Верхняя ветка ограничена функцией
Аргумент изменяется от 3 до 0
Работа А силового поля F при перемещению материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
Интегрирование само по себе тяжелое, главное правильно найти дифференциал функции и не ошибиться с пределами интегрирования.
ЗАДАНИЕ 3.19 Вычислить работу силового поля 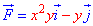
прямая от точки A(-1;0) к точке B(0;1).
Решение: Запишем уравнение прямой, которая проходит через две точки A(-1;0) и B(0;1):
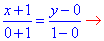
отсюда y=x+1.
Таким образом, имеем дифференциал дуги dy=dx плюс интервал интегрирования [- 1;0].
График прямой приведен на рисунку ниже
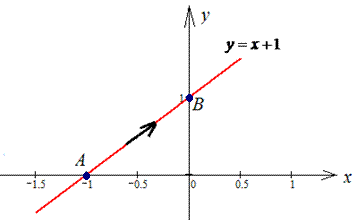
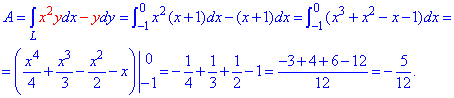
Криволинейный интеграл 2 рода легко сводим к определенному и находим результирующее значение работы.
ЗАДАНИЕ 3.20 Вычислить работу силового поля 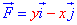
x2+y2=1 от точки A (1;0) к точке B (- 1;0).
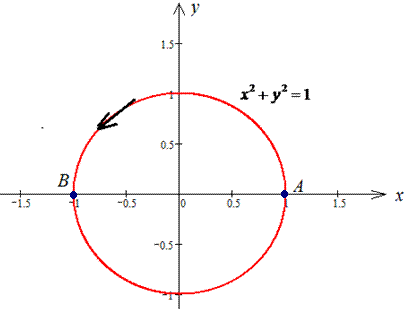
Решение: Построим траекторию материальной точки против движения часовой стрелки по кругу L: x2+y2=9.
Верхнюю его дуга предствим корневой зависимостью
Аргумент при этом изменяется от 1 к -1.
Работа силового поля потрачена на перемещение материальной точки вдоль дуги круга равна интегралу:
Во время интегрирования получим арксинус, который на границах дает число Pi/2.
Еще один раздел где можно применить криволинейный интеграл ІІ рода теперь доступный и известный Вам.
Будьте внимательные в вычислениях и успешной Вам учебы!
Сообщения без ответов | Активные темы
Найти работу силового поля вдоль дуги плоской кривой
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
botanik007 |
|
||
|
Подскажите, как такие решать, особенно второй. 1. Найти работу силового поля [math]mathbf{F}(x,y)=x^2mathbf{i}+frac{1}{y^2}mathbf{j}[/math] вдоль дуги плоской кривой [math]xy=1[/math] заключенной между точками (1;1) и (4;1/4) Напишите, пожалуйста, алгоритм и по возможности решение.
|
||
| Вернуться к началу |
|
||
|
botanik007 |
|
||
|
спасибо )
|
|||
| Вернуться к началу |
|
||
|
mad_math |
|
||
|
1. [math]P(x,y)=x^2,Q(x,y)=frac{1}{y^2},AB:y=frac{1}{x},1leq xleq 4[/math]
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю mad_math «Спасибо» сказали: Medvedo |
|||
|
botanik007 |
|
||
|
спасибо
|
|||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти работу поля F вдоль дуги AB кривой Г, если
в форуме Интегральное исчисление |
haykaz1898 |
3 |
785 |
25 апр 2018, 12:52 |
|
Найти работу силового поля
в форуме Интегральное исчисление |
Ryslannn |
11 |
1614 |
29 ноя 2017, 16:32 |
|
Вычислить работу силового поля
в форуме Интегральное исчисление |
kicultanya |
0 |
321 |
05 окт 2018, 20:04 |
|
Найти работу поля вдоль винтовой линии
в форуме Векторный анализ и Теория поля |
DIDG |
0 |
691 |
21 фев 2014, 14:43 |
|
Найти длину дуги плоской кривой ау^2=х^3 0<=x<=5a
в форуме Интегральное исчисление |
karinakarina |
1 |
327 |
13 дек 2016, 21:02 |
|
Длина дуги плоской кривой
в форуме Интегральное исчисление |
kusya |
1 |
205 |
27 ноя 2016, 14:32 |
|
Площадь плоской фигуры и длина дуги кривой
в форуме Интегральное исчисление |
IvanKnyshov1996 |
2 |
486 |
26 апр 2015, 21:57 |
|
Работа силового поля
в форуме Интегральное исчисление |
paul_woker |
4 |
259 |
02 май 2020, 19:58 |
|
Работа силового поля
в форуме Интегральное исчисление |
Ryslannn |
8 |
414 |
30 ноя 2017, 15:09 |
|
Найти циркуляцию векторного поля F(-y,x) вдоль кардиоиды
в форуме Векторный анализ и Теория поля |
Linc |
1 |
230 |
22 ноя 2021, 16:29 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
6.4.1. Работа силового поля, криволинейный интеграл второго рода
Рассмотрим силовое
поле на плоскости
.
Под
действием силы
от точки А
до точки В
по кривой L
движется точка. Требуется вычислить
работу, совершаемую силой
на пути L
(рис. 6.4.1).
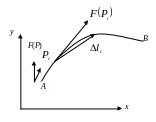
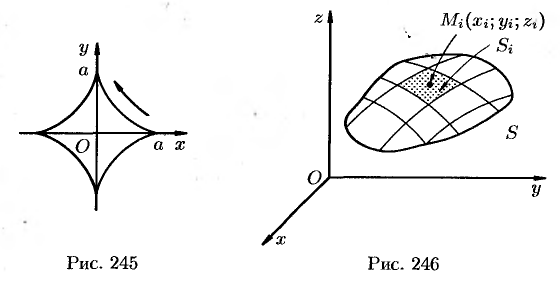
Рис.
6.4.1. Криволинейное движение точки на
плоскости xoy
под действием переменной силы F

Рис.
6.4.2. Прямолинейное движение точки под
действием постоянной силы
Для
прямолинейного
движения и постоянной
силы (
=const)
работа, совершаемая на отрезке
(рис. 6.4.1), равна скалярному произведению
векторов
и l:

где
l
– направленный отрезок, длина которого
равна пройденному пути.
Чтобы
найти работу переменной силы
(x,y)
на криволинейном участке пути L
от А
до В,
очевидно, этот путь нужно разбить на k
маленьких частей так, чтобы каждый
участок пути можно было заменить
направленным отрезком
,
а силу на нем считать постоянной и равной
(Рi)=const
(рис. 6.4.2).
Тогда
работа, совершаемая силовым полем на
i-ом
элементарном участке длиной
приближенно
будет равна скалярному произведению
векторов
Аi
(
(Рi))
.
Вся
работа на пути L
равна сумме элементарных работ
Переходя
к пределу при max
0,
получим точное значение работы,
совершаемой силовым полем на пути L:
Предел,
если он существует, называют криволинейным
интегралом второго
рода, обозначают
,
где
– предельное значение элементарного
направленного отрезка
.
Очевидно, направление
будет совпадать с направлением касательной
к кривой L,
а его модуль равен дифференциалу длины
дуги –
.
Обозначим единичный вектор касательной
–
,
тогда
.
Определение
1. Работа
силового поля
на криволинейном пути L
равна криволинейному интегралу по
кривой L
от скалярного произведения вектора
поля и
–
элемента касательной
к кривой.
,
) (6.4.1)
Выражение
,
)
– называют векторной
формой
криволинейного интеграла второго
рода или
линейным интегралом вектора
.
Скалярное
произведение двух векторов
{P(x,y),
Q(x,y)}
и
{dx,
dy}
можно выразить через их координаты:
(6.4.2)
Правая
часть равенства (6.4.2) представляет собой
координатную
форму
криволинейного интеграла второго рода.
Для пространственной кривой она имеет
вид:
(6.4.3)
Следует
особо подчеркнуть разницу между
физическим смыслом интеграла
– вектора
(второго
рода) и интеграла первого рода
по длине
дуги, который был рассмотрен ранее.
В
последнем суммируются значения скалярной
функции
f(x,y,z),
например, плотности массы или заряда,
умноженные на
–
меры элементарных частей кривой L
(дифференциалы длины дуги), на которые
она дробится. Поэтому, криволинейный
интеграл первого рода не зависит от
того, в каком направлении проходится
кривая L.
Под знаком
криволинейного интеграла второго рода
стоит
скалярное произведение двух векторов,
вектора поля
и элемента касательной
,
при этом направление касательной должно
совпадать с выбранным направлением
обхода кривой
L.
Таким образом, в линейном интеграле
вектора
суммируются значения проекций векторной
величины на касательную к кривой в
различных ее точках. Поскольку скалярное
произведение
зависит от угла между векторами
и
знак интеграла
будет зависеть от выбранного обхода
линии L.
Криволинейный интеграл вектора
вычисляют
так же, как криволинейный интеграл
первого рода, т.е. путем сведения к
линейному (определенному) интегралу.
Для этого должно быть задано уравнение
линии L
и направление
ее обхода (либо
координаты начальной и конечной точек).
Если
плоская линия L
задана в
декартовой системе координат уравнением
у=у(х),
то при сведении интеграла
к
линейному, переменную у
и dy
заменяют их выражением через х
из уравнения линии L:
y
= y(x),
dy
=
dx.
При
параметрическом задании линии L:
x=x(t);
y=y(t),
замену переменных, приводящую к линейному
интегралу, осуществляют по формулам:
х=x(t);
dx=
dt;
y=y(t);
dy=
dt.
Пример
1. Вычислить
работу силового поля
{cosy,
siny}
на
отрезке прямой, соединяющей точки А(2;
–2), В(–2,
2).
Решение.
Работа силового поля равна интегралу
Уравнение
линии L,
проходящей через точки А(2;
–2), В(–2;
2), имеет вид y
= – x
(рис. 6.4.3).
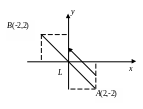
Рис.
6.4.3.
Прямолинейный путь в силовом поле
(иллюстрация к примеру)
Дифференциал
на этой линии dy=–dx.
Переменная х
меняется от 2 до – 2.
Подставляя
в криволинейный интеграл вместо у
– уравнение линии, и заменяя dy
на –
dx
получим
,
,
А
= – 2sin(2рад)
= – 2sin1140
= – 1,827.
В
данном случае работа отрицательна. Она
совершается в направлении, обратном
вектору поля.
Пример
2. Вычислить
криволинейный интеграл
,
где
L
– верхняя часть эллипса
,
обход которого проводится по часовой
стрелке (рис. 6.4.4).
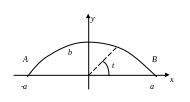
Рис.
6.4.4.
Криволинейный путь в плоском силовом
поле (иллюстрация к примеру)
Решение.
Уравнение эллипса лучше взять в
параметрической форме
L:
x=acost;
y=bsint.
В
этом случае вычисления будут значительно
проще. Найдем значения параметра в
точках начала и конца обхода: в точке
А(–
а;
0) t1
= ,
в точке В(а;
0) t2
= 0.
Выразим
дифференциалы dx
и dy
на данной линии через параметр t:
dx=–asintdt;
dy=bcostdt.
Заменяя
в криволинейном интеграле переменные
х
и у
параметрическим уравнением эллипса и
дифференциалы dx
и dy,
найденными для них значениями на эллипсе,
получим:
=
,
,
.
Таким
образом, при обходе верхней части эллипса
под действием силового поля
,
совершается положительная работа.
Пример
3. Вычислить
криволинейный интеграл
,
где
L
– дуга параболы от точки А(0;0)
до точки В(2;4).
Решение.
Векторное поле параллельно оси ox:
.
Преобразуем криволинейный интеграл в
линейный, т.е. переменную y
заменим уравнением параболы
и расставим пределы изменения х
при движении от точки А
до точки В:
.
Вычисляя данный
интеграл, получим:
.
Работа,
совершаемая силовым полем
на данном отрезке параболы, отрицательна.
Пример
4. Вычислить
криволинейный интеграл
где
L
– дуга параболы у=х2
от точки А(0;0)
до точки В(1;1).
Решение.
Координаты вектора силового поля:
.
Уравнение
линии L:
у=х2.
Дифференциал на этой линии dy=2xdx.
Пределы изменения переменной х:
0; 1. Перейдем к линейному интегралу:
.
Вычисляя линейный
интеграл, получим:
.
Данное
поле на отрезке параболы совершает
положительную работу.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Назначение. Онлайн калькулятор предназначен для нахождения работы силы F при перемещении вдоль дуги линии L.
- Решение онлайн
- Видеоинструкция
Криволинейные и поверхностные интегралы второго рода
Рассмотрим многообразие σ. Пусть τ(x,y,z)— единичный вектор касательной к σ, если σ — кривая, а n(x,y,z)— единичный вектор нормали к σ, если σ — поверхность в R3. Введём векторы dl=τ·dl и dS=n·dS, где dl и dS — длина и площадь соответствующего участка кривой или поверхности. Будем считать, что dσ=dl, если σ — кривая, и dσ=dS, если σ — поверхность. Назовём dσ ориентированной мерой соответствующего участка кривой или поверхности.
Определение. Пусть заданы ориентированное непрерывное кусочно-гладкое многообразие σ и на σ – вектор-функция F(x,y,z)=P(x,y,z)i+Q(x,y,z)+R(x,y,z). Разобьем многообразие на части многообразиями меньшей размерности (кривую – точками, поверхность –кривыми), внутри каждого полученного элементарного многообразия выберем по точке M0(x0,y0,z0), M1(x1,y1,z1), … ,Mn(xn,yn,zn). Посчитаем значения F(xi,yi,zi), i=1,2,…,n вектор-функции в этих точках,умножим скалярно эти значения на ориентированную меру dσi данного элементарного многообразия (ориентированные длину или площадь соответствующего участка многообразия) и просуммируем. Предел полученных сумм если онсуществует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если σ -кривая и поверхностным, если σ — поверхность) второго рода, интеграломвдоль ориентированного многообразия, или интегралом от вектора F вдоль σ, и обозначается в общем случае
, в случаях криволинейного и поверхностного интегралов
соответственно.
Заметим, что если F(x,y,z) — сила, то — работа этой силы по перемещению материальной точки вдоль кривой, если F(x,y,z) — стационарное (не зависящее от времени) поле скоростей текущей жидкости, то
— количество жидкости, протекающей через поверхность S в единицу времени (поток вектора через поверхность).
Если кривая задана параметрически 
то
и для криволинейного интеграла второго рода имеем
Так как dS=n·dS=(cosα, cosβ, cosγ), где cosα, cosβ, cosγ — направляющие косинусы единичного вектора нормали n и cosαdS=dydz, cosβdS=dxdz, cosγdS=dxdy, то для поверхностного интеграла второго рода получаем
Если поверхность задана параметрически 
r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k, (u,v)∈D
то
где 
соответственно.
Если поверхность S может быть задана одновременно уравнениями то поверхностный интеграл второго рода вычисляется по формуле
где D1, D2, D3 — проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно и знак “+” берётся, если угол между вектором нормали и осью, вдоль которой ведётся проектирование, острый, а знак “–“, если этот угол тупой.
Свойства криволинейного и поверхностного интегралов второго рода
Отметим некоторые свойства криволинейного и поверхностного интегралов второго рода.
Теорема 1. Криволинейный и поверхностный интегралы 2-го рода зависят от ориентации кривой и поверхности, точнее
.
Теорема 2. Пусть σ=σ1∪σ2 и размерность пересечения dlim(σ1∩σ2)=n-1. Тогда
Доказательство. Включив в число многообразий разбиения в определении интеграла по многообразию второго рода общую границу σ1 с σ2 получаем требуемое.
Пример №1. Найти работу силы F при перемещении вдоль дуги линии L от точки M0 до точки M1.
F=x2yi+yj;, L: отрезок M0M1
M0(-1;3), M0(0;1)
Решение.
Находим уравнение прямой вдоль отрезка M0M1.
или
y=-2x+1
dy=-2dx
Пределы изменения x: [-1; 0]
Пример №2. Вычислить вдоль кривой
, если t∈[0;π]
Имеем
Пример №3. Вычислить поток вектора f(x,y,z)=(yz,xz,xy)T через часть плоскости x+y+z=a лежащую в первом октанте.
Поток вектора через поверхность равен поверхностному интегралу второго рода Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
где S1, S2, S3 — проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно. Посчитаем первый из них. Имеем 
Поэтому поток вектора через поверхность равен
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Поэтому поток вектора через поверхность равен
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями.
Некоторые приложения криволинейного интеграла II рода
Площадь плоской фигуры
Площадь 
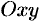

при этом кривая 
Действительно, положив в формуле Остроградского-Грина (56.8) 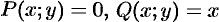
или
Аналогично, полагая 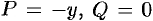
Сложив почленно равенства (56.18) и (56.19) и разделив на два, получим:
Формула (56.17) используется чаще, чем формулы (56.18) и (56.19).
Работа переменной силы
Переменная сила 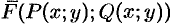

Действительно, пусть материальная точка 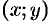
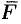
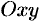

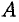
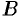
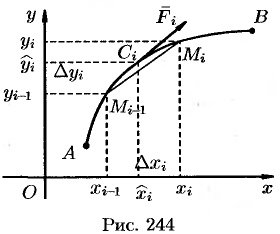
Разобьем кривую 
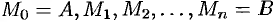

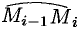
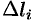
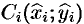
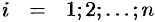
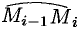
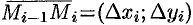
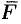
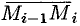
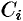
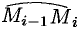
Тогда скалярное произведение 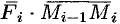
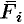
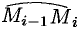
Приближенное значение работы 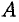
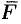
величину
За точное значение работы 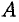
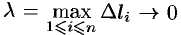
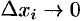
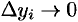
Замечание. В случае пространственной кривой 
Пример №56.6.
Найти площадь фигуры, ограниченной астроидой 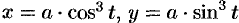
Решение:
При обхождении астроиды в положительном направлении параметр 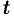
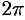
Применяя формулы (56.17) и (56.4), получим:
Пример №56.7.
Найти работу силы 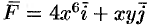
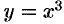
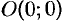
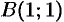
Решение:
По формуле (56.20) находим:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны: