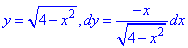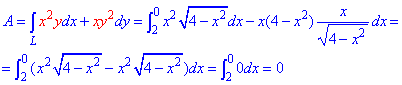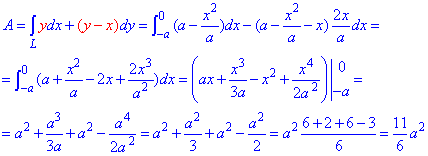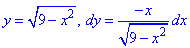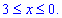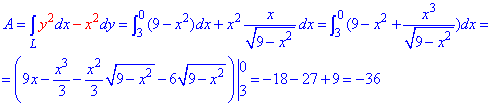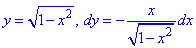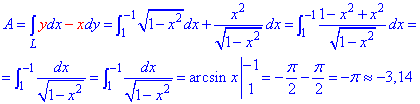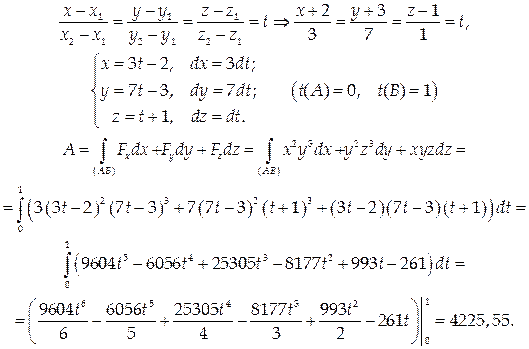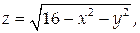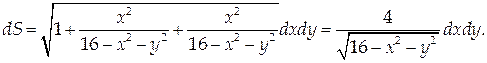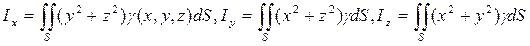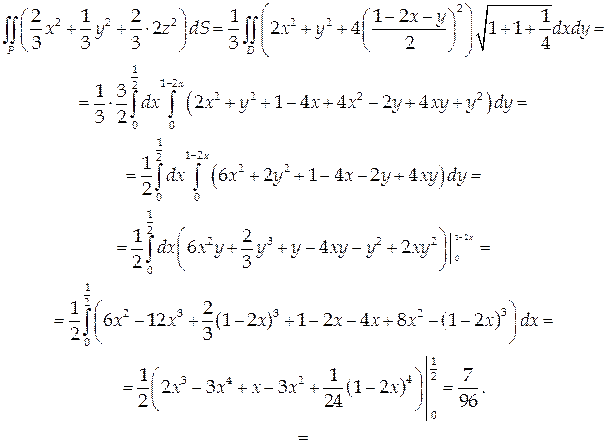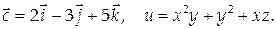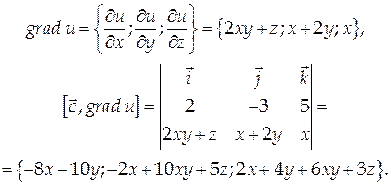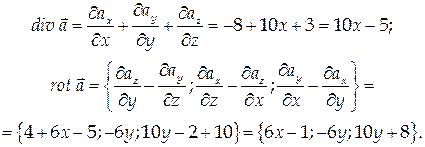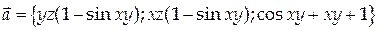Дадим физическую
интерпретацию криволинейного интеграла
второго рода. Если в некоторой области
задано непрерывное силовое поле
,
то при перемещении материальной точки
вдоль гладкой ориентированной кривойL
поле совершает некоторую работу А.
Для её определения разобьём линию L
на
дуг точками
,
,
…,(рис. 16). Пусть
произвольная точка дуги
.
Обозначим– единичный вектор касательнойL
в этой точке и
– длину дуги
.
Р
Рис.5
аботу на дугеможно приближённо вычислить с помощью
скалярного произведения.
Тогда приближённо работа есть.
За работу А
на всей кривой L
естественно принять предел
.
Если этот предел
существует, то он является криволинейным
интегралом I
рода от скалярной функции
,
т.е. это криволинейный интегралII
рода. Таким образом, работа А
по перемещению материальной точки в
непрерывном силовом поле выражается
криволинейным интегралом II
рода:
.
(2)
Покажем, что работа
поля
вдоль любой векторной линии этого поля
отлична от нуля. ПустьL
– векторная линия, тогда
вектор
параллелен
.
Тогда скалярное произведение,
тогда,
причём кривая может быть замкнутой.
Определение 1.
Работа векторного поля
вдоль замкнутой кривойL
называется
циркуляцией
этого поля:
.
Ф
Рис.6
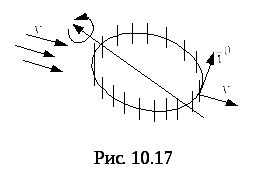
изически её можно интерпретировать
следующим образом. Пусть– поле скоростей
текущей жидкости. Поместим в это поле
колёсико с лопастями, расположенными
по окружностиL
этого колеса (рис.6). Частицы жидкости,
действуя на эти лопасти, будут создавать
вращательные моменты, суммарное действие
которых приводит колесо в движение –
вращение вокруг своей оси. Вращательное
действие поля
в каждой точке будет характеризоваться
проекциейна касательную
,
т.е. скалярным произведением.
Суммирование вращательных действий
жидкости по всему контуру колёсика
приводит к понятию циркуляции вектора.
Ф
изический смысл циркуляции:
циркуляция векторного поля
определяет его вращательную способность
в данном направлении и характеризует
завихрённость поля в этом направлении.
Чем меньше угол между касательной и
вектором поля, тем большеС,
а следовательно и завихрённость.
Пример 2.
Вычислить циркуляцию векторного поля
вдоль замкнутого контура
,
являющегося границей части сферы,
расположенной в первом октанте:,
,
,
причем направление обхода контура
таково, что в плоскостиОху
движение происходит от точки
к
.
Решение.
Контур
состоит из трех кривых
,
каждая из которых является дугой
единичной окружности, лежащей
соответственно в координатной плоскостиОху,
Оуz,
Oxz.
Поэтому
,
.
Найдем интеграл
по кривой
.
Так как криваялежит в плоскостиОху,
то
,
и
,
где,
,
.
Запишем параметрическое уравнение:
,
,
.
Получаем
.
Точно так же
вычисляются интегралы
и
.
При этом.
Следовательно,.
10.3. Потенциальное векторное поле
Определение 2.
Векторное поле
называетсяпотенциальным
в области
,
если существует такое скалярное поле,
что для всех точек этой области
вектор-функцияявляется градиентом этого скалярного
поля:
.
Скалярное поле
называетсяпотенциалом
векторного поля
.
Потенциальное поле является одним из
наиболее простых полей, так как
определяется одной скалярной функцией,
в то время как произвольное векторное
поле – тремя скалярными функциями.
Теорема 1. Если
поле
потенциально, то его потенциал определяется
однозначно с точностью до произвольного
постоянного слагаемого.
Пусть поле
имеет два потенциала
и
,
т.е.и
.
Тогдаи, следовательно,
.
Таким образом, получаем, что.<
Теорема 2. Если
поле
потенциально в областиV,
то работа этого поля (криволинейный
интеграл второго рода) не зависит от
формы пути, соединяющий две любые точки
из V.
Потенциал
с точностью до произвольной постоянной
определяется криволинейным интегралом
второго рода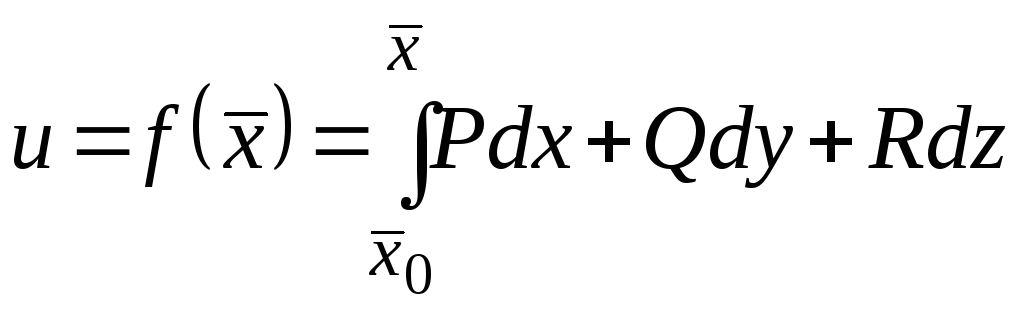
взятому по произвольной кривой,
соединяющей точкии
,
где– фиксированная точка, а
– текущая точка.
Работа А
поля
по некоторому путиL,
соединяющему точки
и
,
вычисляется по формуле (11):
.
Поле
потенциально, тогда существует потенциал
,
причем.
Тогда скалярное произведение
,
Для простоты
преобразований пусть
плоская кривая, заданная параметрическими
уравнениями,
,
,
причем начало в точке,
которой соответствует значение параметра,
а конечной точкисоответствует значение параметра
,
т.е.,
.
Тогда
=
.
Т.е потенциал
определяется по формуле
(3)
Откуда следует,
что работа не зависит от формы пути, а
зависит от положения начальной
и конечной
точек.<
Задача отыскания
потенциала
поля
тесно связано с задачей восстановления
функции трёх переменных по её полному
дифференциалу.
Теорема 3.
Пусть векторное поле задано функцией
,
которая непрерывно дифференцируема в
области.
Для того, чтобы выражение
(4)
было полным
дифференциалом некоторой функции
,
необходимо и достаточно, чтобы полебыло потенциальным.
Необходимость.
Пусть (4) есть полный дифференциал
,
то с одной стороны по определению,
а с другой стороны,
откуда.
Т.е.,
а, следовательно,– потенциальное поле.
Достаточность.
Пусть
– потенциально, тогда существует функция
,
такая, что.
По определению градиента,
,
,
тогда получаем.<
Для того,
чтобы найти функцию
по её полному дифференциалу необходимо
применить формулу (3), т.е. с точностью
до произвольного постоянного слагаемого
вычислить криволинейный интеграл по
любой кривой, соединяющей две точкии
т.е.
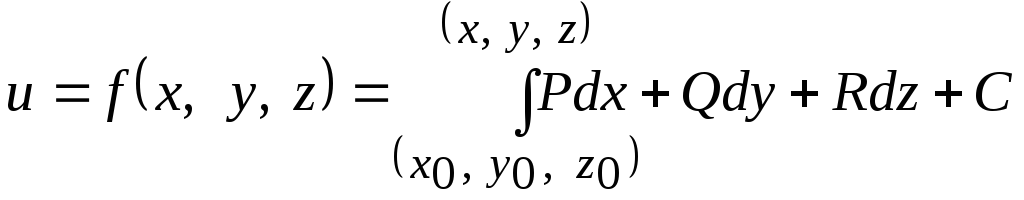
Теперь естественно
возникает вопрос: когда, при каких
условиях векторное поле является
потенциальным?
Теорема 4.
Для того чтобы работа векторного поля
не
зависела от формы пути, соединяющего
две точки в области, необходимо и
достаточно, чтобы циркуляция по любому
замкнутому контуру, лежащему в этой
области, была равна нулю.
Необходимость.
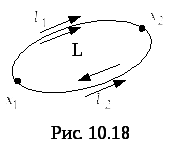
Пусть работа не зависит от пути. Возьмём
контур
(рис. 10.18).
Рис.7
,
Рис.18
.
Достаточность.
Пусть ,
тогда .
Получаем
,
т.е. работа не
зависит от пути.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление работы силового поля по перемещению материальной точки не обходится без применения криволинейного интеграла ІІ рода. Чтобы не повторять в каждой новой статье для криволинейных интегралов те же формулы сразу переходим к анализу готовых примеров.
Вычисление работы силового поля с помощью криволинейного интегралу ІІ рода
ЗАДАНИЕ 3.5 Вычислить работу силового поля 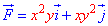
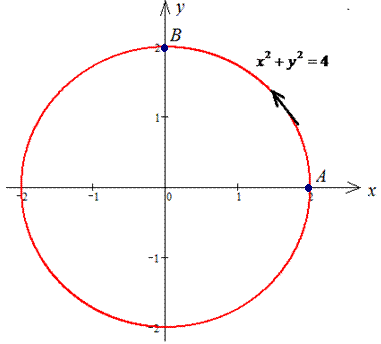
x2+y2=4 от точки A(2;0) к точке B(0;2).
Решение: Построим в декартовых координатах траекторию материальной точки вдоль круга L: x2+y2=4.
Уравнение верхней части полукруга и ее производной равны
В соответствии с точками A(2;0), B(0;2) пределы интегрирования изменяются от 2 до 0.
Не удивляйтесь, что не в обратном порядке. Их всегда нужно выписывать в порядке обхода контуру от точки A к B.
Робота силового поля F по перемещения материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
Внимательно пересмотрите уравнение силового поля и подинтегральную функцию и Вам станет понятно, что и откуда берется. Как вычислить криволинейный интеграл детально расписано в предыдущих статьях (меняем y, dy на ф-и от «х» под интегралом).
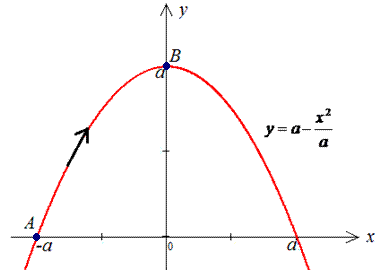
ЗАДАНИЕ 3.10 Найти работу силового поля 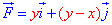
y=a-x2/a от точки A(-a;0) к точке B(0;a).
Решение: Имеем y=a-x2/a — уравнение параболы, находим дифференциал dy=-2x/a*dx и пределы изменения переменной
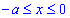
Вычисляем работу силового поля F, потраченную на перемещению материальной точки вдоль вдоль линии L
Криволинейный интеграл ІІ рода находим за первой формулой интегрирования.
ЗАДАНИЕ 3.12 Вычислить работу силового поля 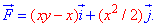
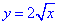
Решение: Строим траекторию материальной точки вдоль корневой функции L: 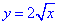
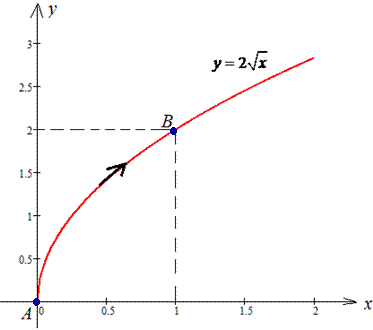
Записываем производную 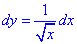
Находим роботу A силового поля F : 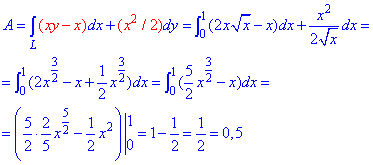
Перед интегрированием превращаем корни к показательной форме записи, а дальше вычисляем за табличными формулами интеграл.
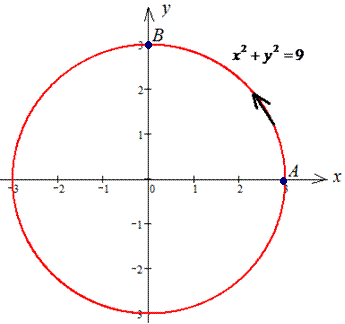
ЗАДАНИЕ 3.14 Вычислить работу силового поля 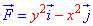
x2+y2=9.
Решение: Наведем траекторию движения материальной точки по кругу L: x2+y2=9.
Верхняя ветка ограничена функцией
Аргумент изменяется от 3 до 0
Работа А силового поля F при перемещению материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
Интегрирование само по себе тяжелое, главное правильно найти дифференциал функции и не ошибиться с пределами интегрирования.
ЗАДАНИЕ 3.19 Вычислить работу силового поля 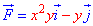
прямая от точки A(-1;0) к точке B(0;1).
Решение: Запишем уравнение прямой, которая проходит через две точки A(-1;0) и B(0;1):
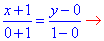
отсюда y=x+1.
Таким образом, имеем дифференциал дуги dy=dx плюс интервал интегрирования [- 1;0].
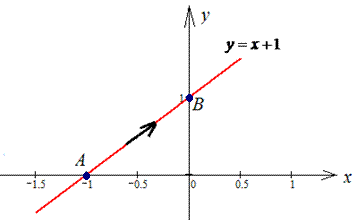
График прямой приведен на рисунку ниже
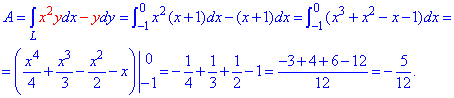
Криволинейный интеграл 2 рода легко сводим к определенному и находим результирующее значение работы.
ЗАДАНИЕ 3.20 Вычислить работу силового поля 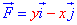
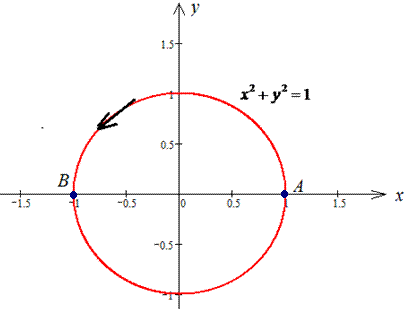
x2+y2=1 от точки A (1;0) к точке B (- 1;0).
Решение: Построим траекторию материальной точки против движения часовой стрелки по кругу L: x2+y2=9.
Верхнюю его дуга предствим корневой зависимостью
Аргумент при этом изменяется от 1 к -1.
Работа силового поля потрачена на перемещение материальной точки вдоль дуги круга равна интегралу:
Во время интегрирования получим арксинус, который на границах дает число Pi/2.
Еще один раздел где можно применить криволинейный интеграл ІІ рода теперь доступный и известный Вам.
Будьте внимательные в вычислениях и успешной Вам учебы!
Пусть поле — непрерывное векторное поле, (L) – кусочно гладкая кривая с выбранным на ней положительным направлением (ориентированная кривая).
Определение 1. Линейным интегралом (обозначается L) вектора вдоль ориентированной кривой (L) называется криволинейный интеграл
(1.7)
Для линейного интеграла справедливы следующие формулы:
(1.8)
=.
Если поле есть силовое поле
, то линейный интеграл (1.7) дает величину работы этого поля вдоль линии (L). Вычисление линейного интеграла в зависимости от задачи может быть проведено по одной из формул “списка” (1.8).
Определение 2. Циркуляцией (обозначается Ц) векторного поля называется линейный интеграл по замкнутой ориентированной кривой (L):
. (1.9)
За положительное направление обхода замкнутой кривой (L) берется то, при котором область, ограниченная кривой, лежит под левой рукой.
Пример 1. Найти линейный интеграл вектора вдоль дуги (L) винтовой линии
от точки A пересечения линии с плоскостью Z=0 до точки В пересечения с плоскостью Z =1.
Решение. Имеем по последней формуле из списка (1.8):
. Точке A соответствует значение параметра T =0, точке B – значение
и, таким образом,



Пример 2. Вычислить работу силового поля вдоль отрезка
прямой, проходящей через точки
и
.
Решение. Работа .
Запишем канонические уравнения прямой .
Отсюда ; параметры
. Вычислим работу:

Пример 3. Вычислить циркуляцию поля вдоль эллипса

Решение. Имеем по формуле (1.9) и (1.8): .
Запишем параметрические уравнения эллипса: . Вычисляя Dx и Dy, получим:


Пример 4. Вычислить циркуляцию векторного поля
вдоль линии L, полученной пересечением конуса
с координатными плоскостями (см. рис.4).
Решение. Линия L состоит из двух отрезков BC и CA, расположенных на координатных плоскостях Oyz и Oxz соответственно, и дуги окружности
. Для циркуляции имеем:
.1) На отрезке BC имеем:
. Следовательно,
. 2) На отрезке CA имеем:
. Следовательно,
. 3) На дуге AB окружности
имеем:
и
=
. Искомая циркуляция поля равна нулю.
Пример 5. Вычислить циркуляцию векторного поля вдоль линии
,
.
Решение. Имеем: . Линия L есть эллипс, получающийся в результате сечения цилиндра
плоскостью
. Найдем параметрические уравнения этой линии. Проекция любой точки этой линии на плоскость Oxy находится на окружности
. Отсюда, полагая
, найдем, что
. Для Z из уравнения
получим:
. Таким образом,
. Находим отсюда:
, и для циркуляции запишем определенный интеграл:


| < Предыдущая | Следующая > |
|---|
Работа вектора вдоль кривой
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Геометрические и физические приложения
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
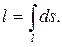
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
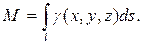
Пример 6.
Найти массу кривой с линейной плотностью 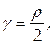
Используем формулу (40) с учетом того, что кривая задана в полярных координатах:
3) Моменты кривой l:
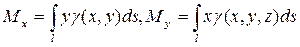
— статические моменты плоской кривой l относительно осей Ох и Оу;
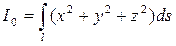
— момент инерции пространственной кривой относительно начала координат;
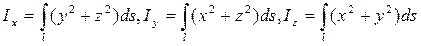
— моменты инерции кривой относительно координатных осей.
4) Координаты центра масс кривой вычисляются по формулам
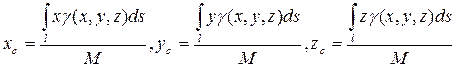
5) Работа силы 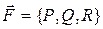
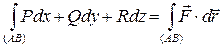
Пример 7.
Вычислить работу векторного поля 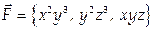
Найдем канонические и параметрические уравнения прямой АВ:
6) Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
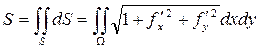
(Ω – проекция S на плоскость Оху).
7) Масса поверхности
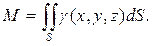
Пример 8.
Найти массу поверхности 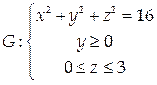
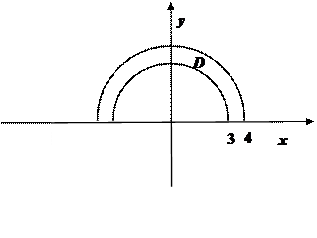
На рассматриваемой поверхности
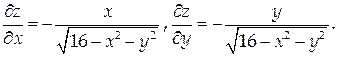
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
Применяя формулу (47) и переходя к полярным координатам, получим:

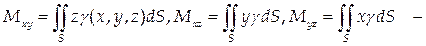
— моменты инерции поверхности относительно координатных осей;
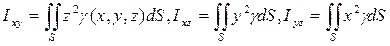
— моменты инерции поверхности относительно координатных плоскостей;
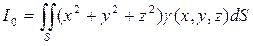
— момент инерции поверхности относительно начала координат.
9) Координаты центра масс поверхности:
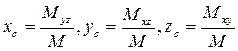
III. Теория поля
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярноеили векторное).
Если в некоторой области задано скалярное поле U(x,y,z), то вектор
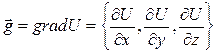
называется градиентомвеличины U в соответствующей точке.
Пусть дано векторное поле 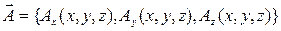
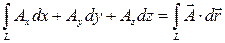
называется линейным интегралом от вектора 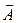
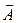
Пример 9.
Вычислить циркуляцию векторного поля 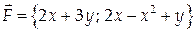
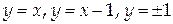
Воспользуемся формулой Грина:
Ротором или вектором вихрявекторного поля A = <Ax, Ay, Az>, где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
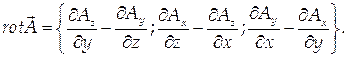
Рассмотрим векторное поле А(М), определенное в пространственной области G, ориентированную гладкую поверхность S 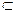
Поверхностный интеграл 1-го рода
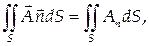
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Пример 10.
Найти поток векторного поля 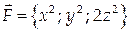
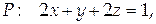
Проекцией данной поверхности на координатную плоскость Оху является треугольник с вершинами в точках А(0;0), В(0;1), С(½; 0). Найдем координаты единичной нормали к плоскости:
Вычислим соответствующий поверхностный интеграл (формула (56)):
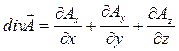
Пример 11.
Найти дивергенцию и ротор векторного поля 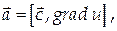
Найдем координаты вектора а:
Векторное поле A = <Ax, Ay, Az> называется потенциальным, если вектор А является градиентом некоторой скалярной функции u = u(x, y, z):
A = grad u = 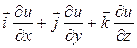
При этом функция и называется потенциалом данного векторного поля.
Пример 12.
Проверить, является ли векторное поле
потенциальным, и в случае положительного ответа найти потенциал и, считая, что в начале координат он равен нулю.
Поле является потенциальным, если выполнены следующие условия:
Следовательно, поле 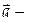
Векторное поле A = <Ax, Ay, Az> называется соленоидальным в области D, если в каждой точке этой области
Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline$
Задача 4. Вычислить потенциальную функцию векторного поля
Поток поля через поверхность
Циркуляция векторного поля
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ overline = (3x-1) overline+ (y-x+z)overline+4z overline, $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline = xz overline -overline+y overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline = z overline+ (x+y)overline+y overline, quad (p): 2x+y+2z=2. $$
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.
http://megalektsii.ru/s51856t7.html http://www.matburo.ru/ex_ma.php?p1=mafield
Сообщения без ответов | Активные темы
Найти работу силового поля вдоль дуги плоской кривой
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
botanik007 |
|
||
|
Подскажите, как такие решать, особенно второй. 1. Найти работу силового поля [math]mathbf{F}(x,y)=x^2mathbf{i}+frac{1}{y^2}mathbf{j}[/math] вдоль дуги плоской кривой [math]xy=1[/math] заключенной между точками (1;1) и (4;1/4) Напишите, пожалуйста, алгоритм и по возможности решение.
|
||
| Вернуться к началу |
|
||
|
botanik007 |
|
||
|
спасибо )
|
|||
| Вернуться к началу |
|
||
|
mad_math |
|
||
|
1. [math]P(x,y)=x^2,Q(x,y)=frac{1}{y^2},AB:y=frac{1}{x},1leq xleq 4[/math]
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю mad_math «Спасибо» сказали: Medvedo |
|||
|
botanik007 |
|
||
|
спасибо
|
|||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти работу поля F вдоль дуги AB кривой Г, если
в форуме Интегральное исчисление |
haykaz1898 |
3 |
785 |
25 апр 2018, 12:52 |
|
Найти работу силового поля
в форуме Интегральное исчисление |
Ryslannn |
11 |
1611 |
29 ноя 2017, 16:32 |
|
Вычислить работу силового поля
в форуме Интегральное исчисление |
kicultanya |
0 |
319 |
05 окт 2018, 20:04 |
|
Найти работу поля вдоль винтовой линии
в форуме Векторный анализ и Теория поля |
DIDG |
0 |
691 |
21 фев 2014, 14:43 |
|
Найти длину дуги плоской кривой ау^2=х^3 0<=x<=5a
в форуме Интегральное исчисление |
karinakarina |
1 |
327 |
13 дек 2016, 21:02 |
|
Длина дуги плоской кривой
в форуме Интегральное исчисление |
kusya |
1 |
205 |
27 ноя 2016, 14:32 |
|
Площадь плоской фигуры и длина дуги кривой
в форуме Интегральное исчисление |
IvanKnyshov1996 |
2 |
486 |
26 апр 2015, 21:57 |
|
Работа силового поля
в форуме Интегральное исчисление |
paul_woker |
4 |
256 |
02 май 2020, 19:58 |
|
Работа силового поля
в форуме Интегральное исчисление |
Ryslannn |
8 |
412 |
30 ноя 2017, 15:09 |
|
Найти циркуляцию векторного поля F(-y,x) вдоль кардиоиды
в форуме Векторный анализ и Теория поля |
Linc |
1 |
230 |
22 ноя 2021, 16:29 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB