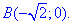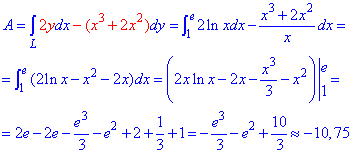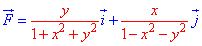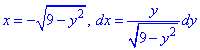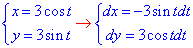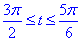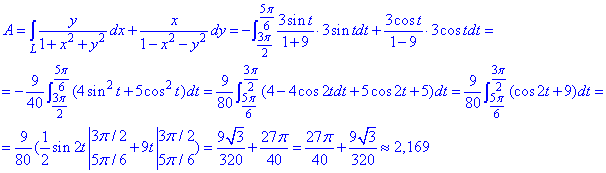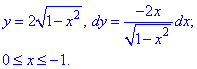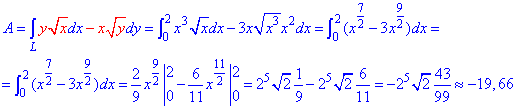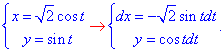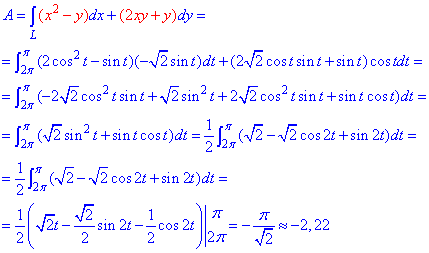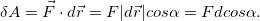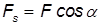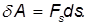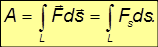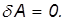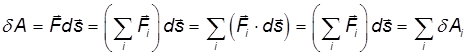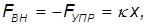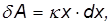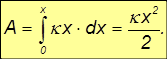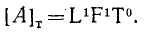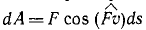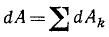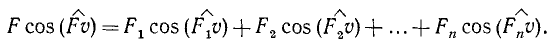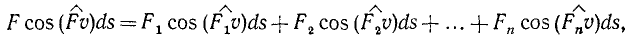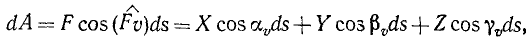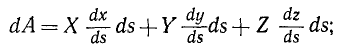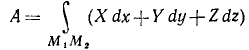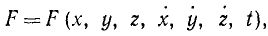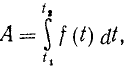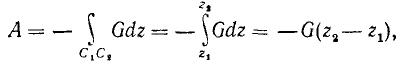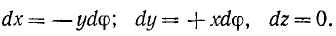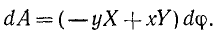Продолжаем предыдущий урок на тему «Применение криволинейных интегралов 2 рода».
Готовые ответы задач на работу силового поля помогут студентам выучить тему, и научат быстро находить нужные интегралы.
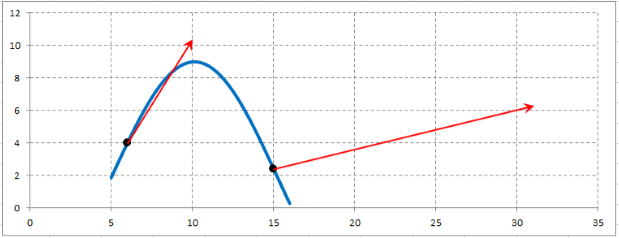
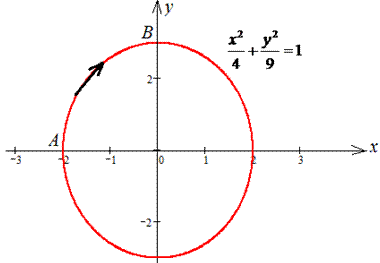
Пример 4.2 Найти работу силы F (
x2/4+y2/9=1 от точки A(- 2;0) к точке B(0;3).
Решение: Запишем уравнение заданного эллипса в параметрическом виде: x=2*cos(t), y=3*sin(t).
Наведем графически траекторию материальной точки вдоль эллипса.
Тогда дифференциал переменных по параметру будет равен dx=-2*sin(t)dt, dy=3*cos(t)dt .
При этом пределы интегрирования ограничатся точками Pi и Pi/2.
Найдем работу силы F по кривой C через криволинейный интеграл ІІ рода : 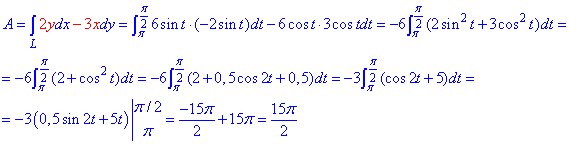
Пересмотрите внимательно формулы интегрирования синуса и косинуса, и понижения степени для таких функций.
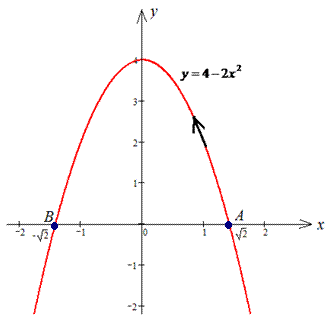
Пример 4.4 Найти работу силы 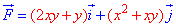
y=4-2x^2 от точки 
Решение: Построим траекторию движения материальной точки вдоль параболы L: y=4-2x2.
Вычисляем дифференциал дуги y=4-2x2, dy=-4x*dx и из условия выписиваем пределы интегрирования
Работа силы F находим с помощью криволинейного интеграла второго рода
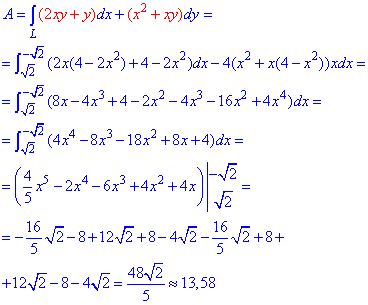
Интегрирование занимает не мало времени и при превращениях можно допустить ошибку, поэтому будьте внимательные в этих местах.
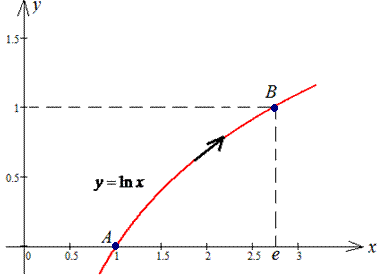
Пример 4.11 Найти работу силы 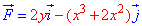
y=ln(x) от точки A(1;0) к точке B(e;1).
Решение: Траектория материальной точки вдоль логарифма имеет вид
Находим дифференциал логарифма y=ln (x), dy=dx/x.
Пределы интегрирования изменяются от единицы к экспоненте.
Работа силы F с помощью криволинейного интеграла ІІ рода примет значение:
Здесь для логарифма применили правило интегрирования частями (u*dv).
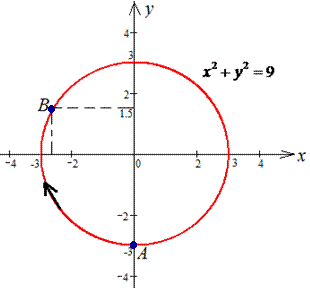
Пример 4.13 Найти работу силы F при перемещении вдоль кривой C:
x2+y2=9 от точки A (0;-3) к точке 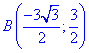
Решение: Построим траекторию движения материальной точки вдоль круга радиусом 3.
Чтобы не выражать две функции (верхняя и нижняя кривая круга) запишем зависимость x(y) и вычислим дифференциал дуги
При этом ордината изменяется от — 3 до 3/2.
Применяя криволинейный интеграл ІІ рода находим роботу силы F при перемещении вдоль круга:
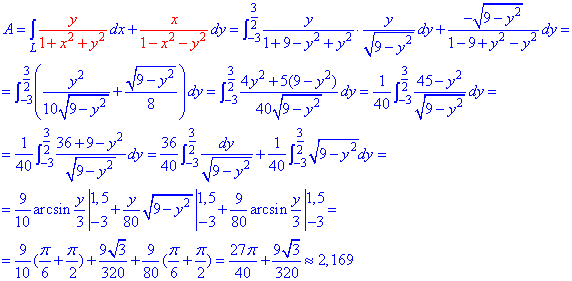
Бороться с корнями во время интегрирования непросто, о чем свидетельствует приведенные вычисления.
Намного проще вычислять интеграл при переходе к полярной системе координат.
Дальше наведем методику интегрирования:
ІІ — способ:
Параметризуэм заданный круг:
Учитывая, что во время движения от точки A(0;-3) к точке 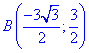
Вычисляем искомый криволинейный интеграл ІІ рода :
В плане вычислений второй метод более легкий, поэтому для круговых и эллиптических форм кривой при симметричном вхождении x, y в уравнение силы рекомендуем переходить к полярной системе координат.
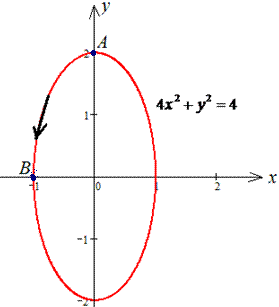
Пример 4.15 Найти работу силы 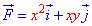
4x2+y2=4 от точки A(0;2) к точке B (-1;0).
Решение: Траектория движения материальной точки по эллипсу приведена ниже
Записываем верхнюю дугу эллипса и ее производную.
Пределы интегрирования изменяются от 0 к -1
Работа силы F через криволинейный интеграл второга рода выражается зависимостью:
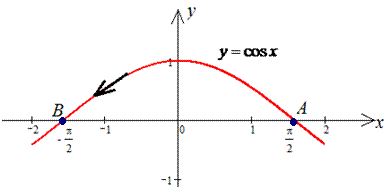
Пример 4.18 Найти работу силы 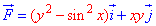
y=cos(x) от точки A(Pi/2;0) к точке B(-Pi/2;0).
Решение: Изобразим траекторию материальной точки вдоль косинуса
Построим дифференциал кривой y=cos(x), dy=-sin(x)*dx.
Он нужен для возведения криволинейного интегралу ІІ рода к определенному.
Находим работу силы F по перемещении вдоль контура интегрированием
Для понижения под интегралом степеней косинуса и синуса применили известные тригонометрические формулы.
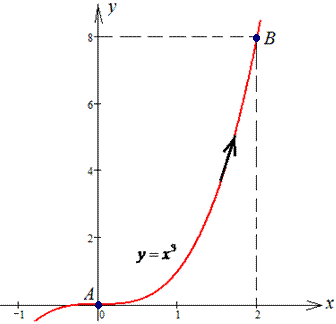
Пример 4.21 Найти работу силы 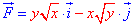
y=x3 от точки A(0;0) к точке B(2;8).
Решение: Построим траекторию материальной точки вдоль кривой y=x3.
Вычисляем дифференциал дуги dy=3x2dx.
Пределы интегрирования приведены на рисунку и в условии.
Работа силы F находим с помощью криволинейного интегралу ІІ рода:
Превращаем все к показательной форме и интегрируем.
Пример 4.23 Найти работу силы 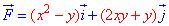
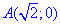
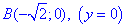
Решение: За инструкцией строим траекторию материальной точки вдоль эллипса: x2+2y2=2.
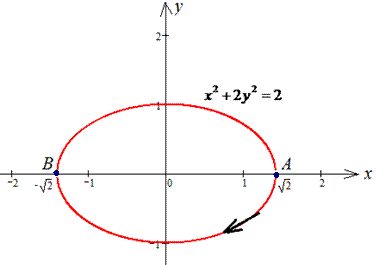
Для простоты вычислений криволинейного интеграла ІІ рода параметризуэм эллипс:
Учитывая, что от точки 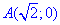
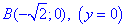
Понижаем степени и интегрируем.
Пример 4.24 Найти работу силы 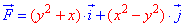
y=1-|x| от точки A(-1;0) к точке B(2;- 1).
Решение: Наведем траекторию материальной точки вдоль модуль функции.
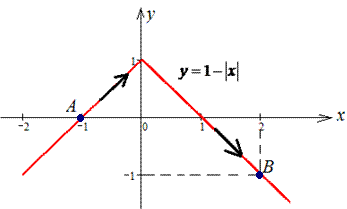
Как ни хотелось встретить задания с разбитием кривой на два интервала, однако одно Пример содержит такое условие. Разделим на две части: y=1+x, тогда пределы равны [-1;0] и дифференциал dy=dx;
На втором участке y=1-x имеем [0;2] и dy=-dx.
Вычисляем работу силы F, потраченную на перемещении точки вдоль модуль функции:
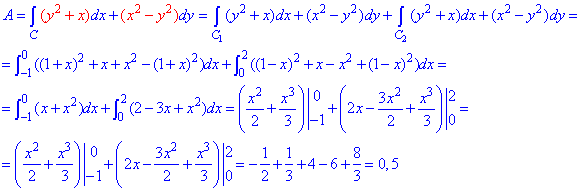
На этом ознакомление из такого сорта примерами завершено.
Больше готовых ответов из курса высшей математики ищите на страницах сайта.
Лекция
2. Работа. Мощность. Теорема об изменении
кинетической энергии точки.
В данной лекции
рассматриваются следующие вопросы:
-
Работа силы.
-
Мощность.
-
Примеры вычисления
работы. -
Потенциальная
энергия -
Кинетическая
энергия -
Теорема об изменении
кинетической энергии точки. -
Теорема моментов.
Изучение данных
вопросов необходимо для динамики
движения центра масс механической
системы, динамики вращательного движения
твердого тела, кинетического момента
механической системы, для решения задач
в дисциплинах «Теория машин и механизмов»
и «Детали машин».
Работа силы. Мощность.
Для
характеристики действия, оказываемого
силой на тело при некотором его
перемещении, вводится
понятие о работе силы.
Рис.16
При
этом работа характеризует то действие
силы, которым определяется
изменение модуля скорости
движущейся точки.
Введём
сначала понятие об элементарной работе
силы на бесконечно малом перемещении ds.
Элементарной работой силы (рис.16)
называется скалярная величина:
,
где —
проекция силы на
касательную к траектории, направленную
в сторону перемещения точки, а -бесконечно
малое перемещение точки, направленное
вдоль этой касательной.
Данное
определение соответствует понятию о
работе, как о характеристике того
действия силы, которое приводит к
изменению модуля скорости точки. В самом
деле, если разложить силу на
составляющие и
,
то изменять модуль скорости точки будет
только составляющая ,
сообщающая точке касательное ускорение
Составляющая же или
изменяет направление вектора
скорости v (сообщает
точке нормальное ускорение),
или, при несвободном
движение изменяет давление на связь.
На модуль скорости составляющая влиять
не будет, т.е.,
как говорят, сила «не
будет производить работу».
Замечая,
что ,
получаем:
. (1)
Таким
образом, элементарная работа силы равна
проекции силы на направление перемещения
точки, умноженной на элементарное
перемещение или
элементарная работа силы равна
произведению модуля силы на элементарное
перемещение и
на косинус угла между направлением силы
и направлением перемещения.
Если
угол острый,
то работа положительна. В
частности, при элементарная
работа .
Если
угол тупой,
то работа отрицательна. В
частности, при элементарная
работа .
Если
угол ,
т.е. если сила направлена перпендикулярно
перемещению, то элементарная работа
силы равна нулю.
Найдем
аналитическое выражение элементарной
работы. Для этого разложим силу на
составляющие ,
,
по
направлениям координатных осей (рис.17;
сама сила на
чертеже не показана).
Рис.17
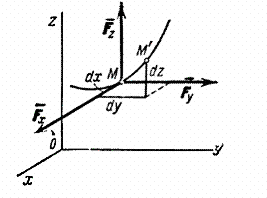
Элементарное
перемещение слагается
из перемещений ,
,
вдоль
координатных осей, где x, y, z —
координаты точки М.
Тогда работу силы на
перемещении можно
вычислить как сумму работ её
составляющих ,
,
на
перемещениях ,
,
.
Но на
перемещении совершает
работу только составляющая ,
причем её работа равна .
Работа на перемещениях и
вычисляется
аналогично. Окончательно
находим: .
Формула дает
аналитическое выражение элементарной
работы силы.
Работа
силы на любом конечном
перемещении М0М1 вычисляется
как интегральная сумма соответствующих
элементарных работ и будет равна:
или
.
Следовательно, работа
силы на любом перемещении М0М1 равна
взятому вдоль этого перемещения интегралу
от элементарной работы. Пределы
интеграла соответствуют значениям
переменных интегрирования в
точках М0 и М1.
Рис.18
Если
величина постоянна
( = const),
то и обозначая перемещение М0М1 через получим:
.
Такой
случай может иметь место, когда
действующая сила постоянна
по модулю и направлению (F= const),
а точка, к которой приложена сила,
движется прямолинейно (рис.18}. В
этом случае и
работа силы .
Единицей
измерения работы в
системе СИ является джоуль (1 дж= 1 hm).
Мощность.
Мощностью называется
величина, определяющая работу, совершаемую
силой в единицу времени. Если работа
совершается равномерно, то мощность
,
где t — время,
в течение которого произведена работа A.
В общем случае
.
Следовательно,
мощность равна произведению касательной
составляющей силы на скорость
движения.
Единицей
измерения мощности в
системе СИ является ватт (1 вт=1 дж/сек). В
технике за единицу мощности часто
принимается 1 лошадиная сила, равная
75 кГм/сек или
736 вт.
Работу,
произведенную машиной, можно измерять
произведением ее мощности на время
работы. Отсюда возникла употребительная
в технике единица измерения работы
киловатт-час (1 квт-ч = 3,6 дж
367100 кГм).
Из
равенства видно,
что у двигателя, имеющего данную
мощность W, сила
тяги будет
тем больше, чем меньше скорость
движения V. Поэтому,
например, на подъеме или на плохом
участке дороги у автомобиля включают
низшие передачи, позволяющие при
полной мощности двигаться с меньшей
скоростью и развивать большую силу
тяги.
Примеры вычисления
работы.
Рассмотренные
ниже примеры дают результаты, которыми
можно непосредственно пользоваться
при решении задач.
1) Работа
силы тяжести. Пусть
точка М, на
которую действует сила тяжести , перемещается
из положения М0 (x0, у0, z0) в
положениеM1 (х1,
у1, z1). Выберем
оси координат так, чтобы ось Oz была
направлена вертикально вверх (рис.19).
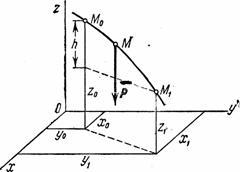
Рис.19
Тогда Рx=0, Рy=0, Pz=
—Р.
Подставляя эти значения и учитывая
переменную интегрирования z:
.
Если
точка M0 выше М1, то ,
где h-величина
вертикального перемещения
точки;
Если
же точка M0 ниже
точки M1 то .
Окончательно
получаем: .
Следовательно,
работа силы тяжести равна взятому со
знаком плюс или минус произведению
модуля силы на вертикальное перемещение
точки ее приложения. Работа положительна,
если начальная точка выше конечной,
и отрицательна, если начальная точка
ниже конечной. Из полученного результата
следует, что работа силы тяжести не
зависит от вида той траектории, по
которой перемещается точка ее приложения.
Силы, обладающие
таким свойством, называются
потенциальными.
2) Работа
силы упругости. Рассмотрим груз М,
лежащий на горизонтальной плоскости и
прикрепленный к свободному концу
некоторой пружины (рис.20,а). Отметим на
плоскости точкой О положение,
занимаемое концом пружины, когда она
не напряжена ( — длина
ненапряженной пружины), и примем эту
точку за начало координат. Если теперь
оттянуть груз от равновесного положения О,
удлинив пружину до величины ,
то на груз будет действовать сила
упругости пружины F,
направленная к точке О.
Рис.20
По
закону Гука величина этой силы
пропорциональна удлинению пружины .
Так как в нашем случае ,
то по модулю .
Коэффициент с называется коэффициентом
жесткости пружины.
В технике обычно измеряют
величину с в H/см, полагая
коэффициент счисленно
равным силе, которую надо приложить к
пружине, чтобы растянуть ее на 1 см.
Найдем
работу, совершаемую силой упругости
при перемещении груза из положения в
положение . Так
как в данном случае ,
,
то получим:
.
(Этот
же результат можно получить по графику
зависимости F от х (рис.20, б), вычисляя
площадь заштрихованной
на чертеже трапеции и учитывая знак
работы.) В полученной формуле представляет
собою начальное удлинение пружины ,
а конечное
удлинение пружины .
Следовательно,
,
т.е. работа
силы упругости равна половине произведения
коэффициента жесткости на разность
квадратов начального и конечного
удлинений (или сжатий) пружины.
Работа
будет положительной, когда ,
т. е. когда конец пружины перемещается
к равновесному положению, и отрицательной,
когда ,
т.е. конец пружины удаляется от равновесия
положения. Можно доказать, что формула
остается справедливой и в случае,
когда перемещение точки М не
является прямолинейным.
Таким
образом, оказывается, что работа
силы F зависит
только от значений и
и не
зависит от вида траектории точки М.
Следовательно, сила упругости также
является потенциальной.
Рис.21
3) Работа
силы трения. Рассмотрим
точку, движущуюся по какой-нибудь
шероховатой поверхности (рис. 21) или
кривой. Действующая на точку сила трения
равна по модулю fN,
где f-коэффициент
трения, а -нормальная
реакция поверхности. Направлена сила
трения противоположно перемещению
точки. Следовательно, Fтр=—fN и
по формуле
.
Если
величина силы трения постоянна,
то , где s-длина
дуги кривой М0М1 по
которой перемещается точка.
Таким
образом, работа
силы трения при скольжении всегда
отрицательна. Величина
этой работы зависит от длины
дуги М0М1 .Следовательно,
сила трения является силой непотенциальной.
4) Работа
силы, приложенной к телу, вращающемуся
вокруг неподвижной оси.
В этом
случае (рис.22) точка приложения
силы движется
по окружности радиуса r.
Элементарная работа, по (1), ,
где .
Рис.22
Поэтому .
Но .
Это
нетрудно установить, разложив силу на
три составляющие (рис. 22). (Моменты
сил и
равны
нулю). Значит,
(2)
В
частности, если момент силы относительно
оси ,
работа силы при повороте тела на
угол равна
. (3)
Знак работы
определяется знаками момента силы и
угла поворота. Если они одинаковы, работа
положительная.
Из
формулы (3) следует и правило определения
работы пары сил. Если пара с
моментом m расположена
в плоскости перпендикулярной оси
вращения тела, то ее работа при повороте
тела на угол
. (4)
Если
же пара сил действует в плоскости не
перпендикулярной оси вращения, то ее
надо заменить двумя парами. Одну
расположить в плоскости перпендикулярной
оси, другую – в плоскости параллельной
оси. Моменты их определяются разложением
вектора момента по
соответствующим направлениям: . Конечно работу
будет совершать только первая пара с
моментом ,
где –
угол между вектором и
осью вращения z,
. (5)
Потенциальная
энергия
Часть пространства,
в которой на помещенную туда материальную
точку действует сила, зависящая от места
положения точки, называетсясиловым
полем.
Причем,
эта сила определяется с помощью
силовой функции u = u(x, y, z). Если
она не зависит от времени, то такое поле
называетсястационарным. Если
во всех точках она одинакова, то поле
– однородное.
Если же проекции
силы на декартовы оси есть частные
производные от силовой функции по
соответствующим координатам
,
,
, (6)
то
такое поле называется потенциальным.
Вычислим
работу силы потенциального поля при
перемещении точки из положения М1 в
положение М2. (рис.
23).
Рис.23
Элементарная
работа,
Это есть полный
дифференциал силовой функции.
Работа на конечном
перемещении
(7)
где u2 и u1 –
значения силовой функции в точках М2 и М1.
Следовательно, работа
силы потенциального поля не зависит от
траектории движения точки, а определяется
лишь значениями силовой функции в
начальном и конечном положениях точки.
Естественно,
если точка вернется в начальное положение,
работа силы будет
равна нулю. Работа окажется равной нулю
и при переходе в другую точку М3,
если там значение силовой функции будет
такое же, как и в начальном положении.
Нетрудно
догадаться, что точки с одинаковыми
значениями силовой функции будут
образовывать целую поверхность. И что
силовое поле – это слоеное пространство,
состоящее из таких поверхностей (рис.
23). Эти поверхности называются поверхностями
уровня или эквипотенциальными
поверхностями. Уравнения
их: u(x, y, z)=C (C –
постоянная, равная значению u в
точках этой поверхности). А силовую
функцию называют, соответственно, потенциалом поля.
Конечно,
эквипотенциальные поверхности не
пересекаются. Иначе существовали бы
точки поля с неопределенным потенциалом.
Поскольку,
при перемещении точки по эквипотенциальной
поверхности работа силы равна
нулю, то вектор силы перпендикулярен
поверхности.
Выберем
среди этих поверхностей какую-нибудь
одну и назовем ее нулевой поверхностью
(положим у нее u=u0).
Работа,
которую совершит силапри
переходе точки из определенного места
М на нулевую поверхность, называют
потенциальной энергией точки в этом
определенном месте М:
. (8)
Заметим, что
потенциальная энергия в одной и той же
точке поля зависит от выбора нулевой
поверхности.
По (8)
силовая функция .
Поэтому проекции силы на декартовы оси,
по (6), так как ,
;
;
(9)
и
вектор силы .
Рассмотрим несколько
потенциальных полей.
1) Поле
силы тяжести.
Вблизи
поверхности Земли сила тяжести во всех
точках одинакова ,
равна весу тела. Значит, это силовое
поле однородное. Так как при перемещении
точки в горизонтальной плоскости работа
силы равна нулю, то эквипотенциальными
поверхностями будут горизонтальные
плоскости (рис. 24), а уравнения их: u = z = C.
Рис.24
Если
нулевой поверхностью назначить
плоскость xOy, то
потенциальная энергия точки в
положении М будет
равна работе силы тяжести:
.
2) Поле
упругой силы.
При
деформации упругого тела, например
пружины, появляется сила. То есть около
этого тела возникает силовое поле, силы
которого пропорциональны деформации
тела и направлены в сторону недеформированного
состояния. У пружины – в точку М0,
где находится конец недеформированной
пружины (рис. 25).
Рис.25
Если
перемещать конец пружины так, чтобы
длина ее не изменялась, то работа упругой
силы будет
равна нулю. Значит эквипотенциальными
поверхностями являются сферические
поверхности с центром в точке О.
Назначим
нулевой поверхностью сферу, проходящую
через точку М0,
через конец недеформированной пружины.
Тогда потенциальная энергия пружины в
положении М: .
При таком выборе
нулевой поверхности потенциальная
энергия всегда будет положительной
(П>0), и в растянутом, и в сжатом состоянии.
Теорема об изменении
кинетической энергии точки.
Рассмотрим
точку с массой т, перемещающуюся
под действием приложенных к ней сил
из положения M0 ,
где она имеет скорость , в
положение М1 ,
где ее скорость равна .
Для
получения искомой зависимости обратимся
к уравнению выражающему
основной закон динамики. Проектируя
обе части этого равенства на касательную к
траектории точки М, направленную
в сторону движения, получим:
Стоящую слева
величину касательного ускорения можно
представить в виде
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
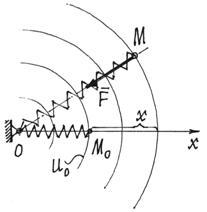
Работа силы вдоль вектора
как найти работу силы вектора F(1,-2,3)на пути из точки А (0,0,1) в точку В (-1,-1,-1)
Работа силы по перемещению на пути из точки А в точку B определяется как скалярное произведение вектора силы на вектор перемещения. Вектор перемещения равен АВ = (-1-0; -1-0 -1-1) = (-1; -1: -2). Скалярное произведение векторов, заданных своими координатами (x1, y1, z1) и (x2, y2, z2), вычисляется по формуле (x1x2 + y1y2 + z1z2). Подставляя сюда координаты векторов силы и перемещеня, получаем ответ A = -5. Обратите внимание на знак минус перед числом.
Работа силы вдоль вектора
Прежде, чем Вы начнёте скачивать свои варианты, попробуйте решить задачу по образцу, приведённому ниже для варианта 1.
Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6
Вариант 7 Вариант 8 Вариант 9 Вариант 10 Вариант 11 Вариант 12
Вариант 13 Вариант 14 Вариант 15 Вариант 16 Вариант 17 Вариант 18
Вариант 19 Вариант 20 Вариант 21 Вариант 22 Вариант 23 Вариант 24
Вариант 25 Вариант 26 Вариант 27 Вариант 28 Вариант 29 Вариант 30
10.1. Найти работу силы F при перемещении вдоль линии L от точки M к точке N.
L – отрезок MN, M(-4, 0), N(0, 2).
Решение
Построим рисунок.
Уравнение прямой MN:
или
Дифференциал
При этом на отрезке MN x изменяется от -4 до 0.
4.1. Работа силы
Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).
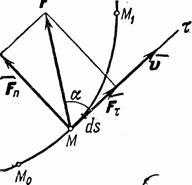
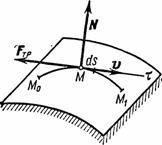
Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.
Рис 4.1. Элементарная работа
Элементарная работа силы 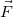
Работа — скалярная величина, ее знак зависит от знака 
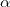
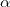
— это проекция силы F на направление перемещения. Следовательно,
Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:
При перемещении вдоль оси x работу графически можно представить как площадь под кривой Fx(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.
Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = Fx(x)
Если перемещение ортогонально силе, то 
Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и 

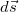

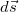
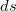
Если на тело действует несколько сил, то
то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.
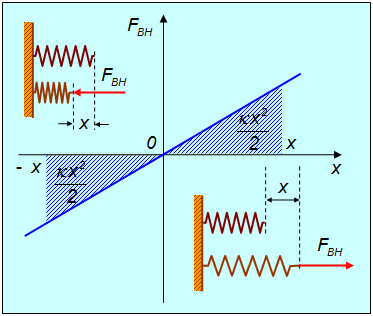
Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью 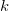
где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).
Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины
Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид
так что для полной работы упругой деформации пружины получаем
Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.
Мощность и работа силы в теоретической механике
Содержание:
Работа силы м мощность силы:
«Работа — это изменение формы движения, рассматриваемое с его количественной стороны» (Энгельс)
Понятие работы
Энергия может переходить из одного вида в другие. Например, потенциальная энергия воды, поднятой плотиной на гидроэлектростанции, переходит в кинетическую энергию вращающихся турбин, которая в свою очередь превращается в электрическую энергию, по проводам передается на большие расстояния, чтобы опять перейти в кинетическую энергию станков, в тепловую энергию электропечей, в световую, в звуковую и в прочие виды энергии. При всех этих явлениях исчезает (или возникает) такое же количество каждого вида энергии, сколько возникает (или исчезает) энергии всех прочих видов. Это изменение энергии, изменение формы движения, рассматриваемое с количественной стороны, Энгельс называет работой.
Из множества различных видов движения в теоретической механике интересуются только механическим движением. Переход механического движения в немеханическое или же, наоборот, немеханического в механическое происходит на протяжении некоторого пути и зависит от действующих сил. Поэтому понятие работы в механике связано с понятиями перемещения и силы.
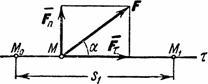
Работу постоянной силы при прямолинейном движении выражают произведением модуля силы на величину перемещения материальной частицы и на косинус угла между направлением силы и перемещением А = Fs cos α
Работа постоянной силы при прямолинейном движении
Знакомство с понятием работы силы в механике начнем с частного случая — работы постоянной силы при прямолинейном движении точки ее приложения.
Пусть к некоторой материальной частице приложена сила F, постоянная по величине и по направлению. Пусть точка приложения силы переместилась на прямолинейный отрезок s . В таком случае произведение
выражает работу постоянной силы F при прямолинейном движении и характеризует механическое воздействие на материальную частицу со стороны других материальных объектов на данном пути.
Работа является скалярной величиной, она не имеет направления и вполне характеризуется величиной и знаком. В формуле (218) модуль силы F и длина пути s всегда положительны. Знак « + » или «—» определяются знаком косинуса угла α между направлением силы и перемещения или, так как при прямолинейном движении точки перемещение совпадает с направлением скорости υ, косинусом угла между направлением силы и скорости. Работа положительна, если угол (Fυ) острый, и отрицательна, если он тупой. Если направление F совпадает с направлением перемещения, то угол (
Если же сила направлена противоположно перемещению, то (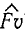
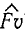
Сила, перпендикулярная к перемещению, работы не совершает, так как cos 90° = 0.
Определим размерность работы. В физической системе единиц
Единицей работы в СИ является джоуль 2 — работа силы в 1 ньютон, действующей по направлению перемещения на пути в 1 метр (1 дж= 1 н ∙ 3t = l кг ∙ м 2 ∙ ceκ -2 ).
Размерность работы в технической системе единиц
Если сила выражена в кГ, а длина — в м, то единицей работы является 1 килограммометр.
Размерности работы и кинетической энергии одинаковы.
Элементарной работой силы называют работу силы на столь малом перемещении точки ее приложения, при котором изменением силы можно пренебречь:
Элементарная работа силы
В общем случае, если сила переменна или движение точки приложения силы криволинейное, определять работу силы по (218) нельзя. Но, разбив мысленно весь путь на такие маленькие участки, которые можно считать прямолинейными и на которых можно пренебречь изменением величины и направления силы, мы определим на каждом из этих участков работу, называемую элементарной работой силы:
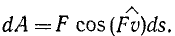
В этом равенстве ds выражает длину элементарного перемещения и является величиной всегда положительной.
Зная работу силы (219) на отдельных элементах пути, можно определить работу на конечном участке. Докажем некоторые теоремы о работе силы.
Элементарная работа равнодействующей равна сумме элементарных работ составляющих:
Теорема об элементарной работе равнодействующей. Пусть к точке О приложен пучок сил F1, F2. Fn. Обозначим равнодействующую этого пучка F. Спроецируем все силы пучка и равнодействующую на направление скорости точки О и приравняем проекцию равнодействующей сумме проекций составляющих:
Умножив теперь каждый член этого равенства на длину ds элементарного перемещения точки приложения сил, найдем, что элементарная работа равнодействующей равна сумме элементарных работ составляющих:
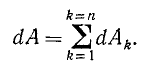
Под суммой следует понимать, конечно, алгебраическую сумму, потому что работа не имеет направления, но имеет знак.
Элементарная работа силы связана с проекциями силы на оси координат соотношением: dA = Xdx+ Ydy + Zdz
Выражение элементарной работы через проекции силы на оси координат
Разложим силу F на составляющие по осям координат и определим элементарную работу силы по сумме работ ее составляющих. Пусть составляющие силы направлены в положительном направлении осей координат. Тогда углы между составляющими силы и скоростью являются углами между скоростью и положительными направлениями осей координат, а их косинусы определяются формулами (62) направляющих косинусов скорости. В таком случае имеем
или, подставляя значения направляющих косинусов,
сокращая на ds, получаем окончательно
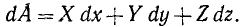
Формула (221) имеет очень большое значение в динамике. При. выводе этой формулы мы считали X, Y и Z направленными положительно по осям координат. Если какие-либо из составляющих силы направлены в противоположные стороны, то иным станет знак соответствующего косинуса. Поэтому в (221) X, Y и Z являются не модулями составляющих, а проекциями силы на оси координат, т.е. определяются не только величиной, но и знаком. Кроме того, в отличие от (219), где всегда ds>0, в (221) величины dx, dy и dz являются дифференциалами координат точки приложения силы и могут быть как положительными, так и отрицательными.
Заметим, что в общем случае дифференциальный трехчлен X dx + Y dy + Z dz не является полным дифференциалом и обозначение элементарной работы dA не следует понимать как полный дифференциал от А.
Работу силы на данном пути выражают пределом суммы всех элементарных работ силы на элементарных перемещениях, из абсолютных величин которых составляется данный путь:
Работа силы на данном пути. Возьмем какие-либо два положения M1 и M2 точки на ее криволинейной траектории. Работа А силы F на конечном перемещении M1M2 выразится суммой элементарных работ силы F на всех элементарных перемещениях, на которые разбит конечный участок пути M1M2.
Эта сумма состоит из бесчисленного множества бесконечно малых слагаемых. Такую сумму называют криволинейным интегралом, взятым по дуге M1M2, и обозначают так:
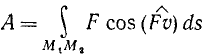
или, если воспользоваться выражением элементарной работы через проекции силы на оси координат,
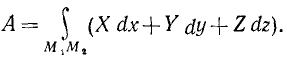
Если на точку действуют несколько сил, то, очевидно, работа равнодействующей на конечном участке пути равна сумме работ составляющих на том же участке пути.
Так как сила, вообще говоря, зависит от координат точки ее приложения, от проекций скоростей точки и от времени:
то мы можем вычислить интеграл (222′) только в случае, если известно движение точки. Подставив тогда вместо 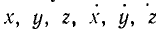
где t1 и t2 — мгновения, соответствующие положению точки в M1 и M2.
Работа графически выражается площадью, ограниченной кривой, изображающей зависимость проекции силы на скорость от пути, осью абсцисс и крайними ординатами
Графическое определение работы
Ввиду сложности математического вычисления работы па практике часто пользуются для этой цели графическим методом. Будем откладывать по оси абсцисс длину пути, пройденного точкой, а по оси ординат — соответствующую проекцию силы на направление скорости, учитывая и знак проекции. Получим некоторую кривую, изображающую зависимость между проекцией силы на направление скорости и путем точки. Площадь, ограниченная этой кривой, осью абсцисс и двумя крайними ординатами, изображает работу силы на данном пути. Если кривая или часть ее расположена по отрицательную сторону, вниз от оси абсцисс, то соответствующая площадь изображает отрицательную работу.
Для построения графика зависимости силы от пути имеются различные приборы. В частности, специальный прибор — индикатор— служит для записи давления в цилиндре в зависимости отхода поршня. Работу, вычисленную при помощи индикаторной диаграммы, т.е. диаграммы, начерченной этим прибором, называют индикаторной работой.
Работа силы тяжести не зависит от вида траектории центра тяжести тела и равна произведению веса тела на изменение высоты центра тяжести тела: AG=Gh
Работа силы тяжести
Складывая веса всех частиц тела, заменим их одной силой G, равной весу тела и приложенной в центре тяжести С. Пусть при движении тела центр тяжести тела переместился из C1(x1, yl, z1) в C2 (x2, y2, Z2) (рис. 210). Определим проекции веса на оси координат, считая, что Oz направлена вертикально вверх:
и, подставив их в (222′), получим под знаком интеграла полный дифференциал, а потому
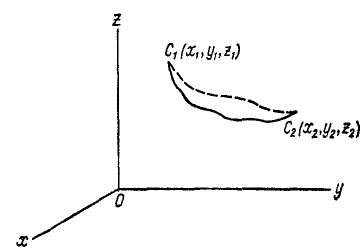
Рис. 210
Следовательно, работа силы тяжести не зависит от вида траектории точек тела и равна произведению веса тела на разность начальной и конечной высот центра тяжести. Если тело опускается, то сила тяжести тела совершает положительную работу, а если поднимается, то отрицательную. Так, например, если человек поднял гирю весом 10 кГ на высоту одного метра (безразлично—по вертикали или по иной траектории), то работа силы тяжести равна —10 кГ∙ м, а работа человека на преодоление силы тяжести равна +10 кГ∙ м.
Элементарная работа силы, приложенной к телу, закрепленному на неподвижной оси, равна произведению момента силы относительно оси вращения на бесконечно малый угол поворота: dА = Mdφ
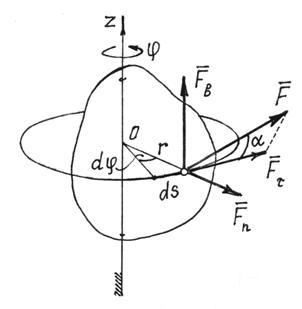
Работа силы, приложенной к вращающемуся телу
Пусть тело вращается (или может вращаться) вокруг неподвижной оси и к какой-либо точке К этого тела приложена сила F. Примем ось вращения тела за ось Oz прямоугольной системы координат. Элементарная работа силы выразится равенством
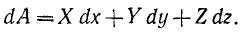
Припомним формулы Эйлера, связывающие проекции вращательной скорости точки К (х, у, z) с угловой скоростью и координатами этой точки:
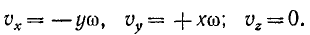
Умножая эти равенства на dt, найдем приращения координат точки приложения силы:
Подставим эти выражения dx, dy и dz в формулу (221)
Разность, стоящая в скобках, выражает момент данной силы относительно оси вращения Oz:
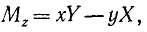
а следовательно, элементарная работа силы, приложенной к вращающемуся телу, равна произведению момента силы относительно оси вращения на дифференциал угла поворота:
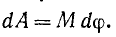
Если на тело действует несколько сил, то, составив такие равенства для определения работы каждой из них и просуммировав, найдем, что элементарная работа всех сил равна произведению главного момента сил относительно оси вращения на dφ.
Чтобы определить работу силы, действующей на тело при его повороте от φ1 до φ2, надо проинтегрировать уравнение (224) в этих пределах, выразив момент силы в функции угла поворота:
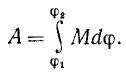
В частном случае постоянного момента силы
работа равна произведению момента силы на угол поворота тела.
Задача №1
Однородный массив ABED, размеры которого указаны на чертеже (рис. 211, а), весит 4 Т. Определить работу, которую необходимо произвести, чтобы опрокинуть его вращением вокруг ребра D.
Рис. 211
Решение. 1-й способ. Рассматриваем опрокидывание массива. Какие силы действуют на массив? Их две: вес массива G=4 Т, приложенный в его центре тяжести С, и реакция фундамента. Во время опрокидывания реакция приложена в ребре D, вокруг которого происходит опрокидывание (рис. 211,6), как известно из статики). Но во время опрокидывания ребро D неподвижно, поэтому работа реакции равна нулю. Работу веса (силы тяжести) определим по (223). Для опрокидывания массива достаточно повернуть его до положения неустойчивого равновесия, изображенного на рис. 211, в, при котором центр тяжести находится в вертикальной плоскости, проходящей через ребро D; далее массив опрокинется сам. Имеем
Такова работа силы тяжести при опрокидывании массива. Чтобы опрокинуть массив, надо произвести работу, такую же по величине и обратную по знаку.
2-й способ. Несколько сложнее получится решение задачи, если мы воспользуемся формулой (225) о работе сил, приложенных к вращающемуся телу.
На поворачиваемый вокруг ребра D массив действуют вес и реакция в ребре D. Момент реакции относительно оси вращения равен нулю, следовательно, равна нулю и работа реакции. Момент веса — величина переменная — равен произведению силы 4 T на плечо CD cos φ, где φ (см. рис. 211, б) —угол, составляемый CD с горизонтальной плоскостью:
Определим пределы интегрирования. При начале работы массив стоял вертикально, высота центра тяжести была 4 м и
Угол считаем отрицательным, так как отсчет производим по ходу часов:
В конечном положении (см. рис. 211, в)
Подставляя в (225), получаем
Мы определили работу восстанавливающего момента, вызванного силой тяжести и стремящегося восстановить устойчивое равновесие массива. Работа на опрокидывание массива вращением вокруг ребра D равна ей по величине и противоположна по знаку.
Задача №2
Определить работу на преодоление силы земного притяжения при запуске на высоту 30 000 м ракеты массой m = 2000 кг, считая силу притяжения изменяющейся по закону всемирного тяготения. Радиус земного шара принять R = 6 370 000 м.
Решение. На ракету действует сила, направленная к центру Земли и равная
где k — постоянный коэффициент пропорциональности, M — масса Земли, — масса ракеты и x = h + R — расстояние ракеты от центра Земли.
Обозначая kM через μ, имеем
При x=R ракета находится на поверхности Земли и F = mg,
Зная μ и k, можно определить массу Земли, потому что k = μ : M.
Работу переменной силы F на перемещение ракеты с поверхности Земли на высоту h= 30 000 м определим по (222):
Отрицательный знак показывает, что при подъеме ракеты сила тяготения ракеты к Земле направлена против движения. Чтобы преодолеть эту силу на заданном расстоянии, надо совершить работу, такую же по величине, но положительную по знаку.
Ответ. A = + 5 621 262 369 дж.
Задача №3
Доказать, что сумма работ внутренних сил абсолютно твердого тела при всяком перемещении тела равна нулю.
Решение. Рассмотрим две точки А и В твердого тела (рис. 212). Силы взаимодействия этих точек всегда равны между собой и направлены по прямой AB в противоположные стороны.
Проекции скоростей точек А и В на прямую AB всегда равны между собой:
Рис. 212
Поэтому при любом перемещении работы сил взаимодействия точек A и В равны по величине, но обратны по знаку, и сумма работ равна нулю
Доказательство проведено для двух точек абсолютно твердого тела, за которые мы можем принять любые точки тела, а потому оно относится ко всем точкам твердого тела. В случае упругого тела или изменяемой системы точек сумма работ внутренних сил не равна нулю. Так, например, при падении камня на Землю силы взаимодействия между камнем и Землей (внутренние силы системы Земля —камень) равны и противоположны, но сумма работ этих сил не равна нулю.
Ответ. Сумма работ всех внутренних сил в абсолютно твердом теле при всяком перемещении тела равна нулю.
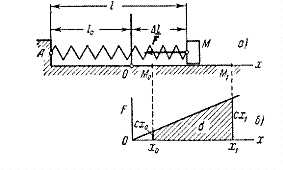
Работа упругой силы равна половине произведения коэффициента жесткости на квадрат деформации:
Работа упругой силы. Определим работу упругой силы F пружины при растяжении ее на λ см, если для растяжения этой пружины на 1 см необходима сила с кГ (рис. 213). Сначала определим работу, которую необходимо совершить для растяжения этой пружины на λ см.
Рис. 213
Согласно одному из основных законов теории упругости и сопротивления материалов, называемому законом Гука, растяжение нагруженного тела прямо пропорционально нагрузке:
де F — нагрузка, х—растяжение и с — коэффициент жесткости.
Подставляя это значение F в (221) и интегрируя в пределах от О до λ, найдем работу, необходимую для искомой деформации пружины:
(227)
Если к пружине приложить силу, например растягивать пружину рукой, то со стороны пружины возникнет реакция, называемая упругой реакцией, или упругой силой, пружины. По принципу равенства действия и противодействия упругая сила равна и противоположна растягивающей силе F, а поэтому работа упругой силы определяется найденным значением. Знак работы упругой силы отрицателен, если сила упругости направлена против деформации, т. е. если деформация увеличивается, и положителен, если деформация уменьшается.
Задача №4
Применить графический метод для вывода формулы (227).
Решение. Будем откладывать (рис. 214) по оси абсцисс растяжение пружины, а по оси ординат—силу F, потребную для этого растяжения, затем построим по точкам кривую зависимости между силой и перемещением точки приложения силы. В нашем случае это кривая первого порядка, т. е. прямая линия.
Рис. 214
Первую точку поставим в начале координат, так как при отсутствии растягивающей силы растяжение пружины равно нулю. Чтобы растянуть пружину на 1 см, нужна сила с кГ, поэтому вторая точка кривой имеет координаты х=1, у =с Если сила с кГ будет продолжать действовать на пружину, то пружина будет оставаться растянутой на один сантиметр, но чтобы растянуть пружину еще на один сантиметр, надо увеличить силу еще на с кГ. Следовательно, координаты третьей точки x=2, y=2c и т. д. Для растяжения пружины на λ си нужна сила в cλ кГ. Точка x = λ, y = cλ лежит на прямой, соединяющей все нанесенные точки. Проведя ординату крайней точки, получим треугольник с основанием λ и высотой cλ.
Ответ. Работа выражается площадью этого треугольника, т. е.
Заметим, что работа упругой силы выражается полученным равенством не только в рассмотренном нами частном случае. Эта формула относится в равной мере ко всем случаям упругой деформации, в которых упругая реакция подчиняется закону Гука F = сх, где х—перемещение точки приложения реакции, отсчитанное от положения этой точки при недеформированном состоянии тела, ас — постоянный коэффициент. Сюда относятся растяжение и сжатие прямолинейного бруса, изгиб балки и т. п.
Величину, характеризующую быстроту приращения работы Силы и выражающуюся отношением элементарной работы к дифференциалу времени, называют мощностью силы:
Мощность силы
Одну и ту же работу можно произвести за различное время. Величину, характеризующую быстроту приращения работы, называют мощностью силы и обозначают буквой N. Разделив работу, произведенную силой, на время, в течение которого эта работа произведена, получим значение средней мощности силы:
B этом смысле говорят, хотя и несколько нечетко, что средняя мощность — это работа за единицу времени. При таком определении получается, что мощность является работой, или элементарной работой, чего не может быть, так как мощность имеет свою размерность. В физической системе единиц
Единицей мощности в СИ является мощность силы, производящей работу в один джоуль за одну секунду. Эту единицу называют ватт1 и обозначают вт. На практике часто употребляют единицу мощности киловатт (квт):
1 κвт= 1000вт =l02 кГ •м/сек.
В технической системе единиц
В технической системе в качестве единицы мощности силы обычно применяют кГм/сек. Употребляют также другую единицу мощности, называемую лошадиной силой:
1 л. с. = 75 кГ • м/сек = 736 вт.
Чем меньше промежуток времени, за который определена средняя мощность силы, тем ближе она соответствует мощности в данное мгновение, которую мы определим в пределе, если будем уменьшать промежуток времени, сохраняя начало этого промежутка:
(228)
Таким образом, мощность силы выражают отношением элементарной работы к дифференциалу времени.
При некоторых частных выражениях работы мощность можно определить по другим формулам. Так, например, если сила направлена по скорости, то dA=Fds, и, подставляя в (228), найдем
т. е. мощность можно выразить произведением силы на скорость. При езде на автомобиле по ровной хорошей дороге, где нужно получить большую скорость, но не надо преодолевать большие сопротивления, включают высшие передачи, а при подъеме или на плохой дороге, где нужно развить при полной мощности возможно большую силу тяги, хотя бы и за счет потери скорости, включают низшие передачи.
Если сила выражена в килограммах, скорость —в км/ч, а мощность надо выразить в л. с., то формула (229) принимает следующий вид:
При вращательном движении тела подставим вместо dA его выражение (224):
(230)
т. е. мощность выражается произведением вращающего момента и угловой скорости.
Задача №5
Тягач, развивая мощность 80 л. с., тянет по горизонтальной ледяной дороге со скоростью 15 км/ч сани с грузом 36 т. Определить коэффициент трения саней о дорогу.
Решение. За основные единицы примем: L — в км, F —в кГ, T — в ч.
На сани действуют следующие силы: 1) вес 36 000 кГ, направленный вертикально вниз, 2) реакция дороги, направленная вертикально вверх; 3) сила тяги тягача, направленная горизонтально вперед по ходу саней, и 4) сила трения полозьев о дорогу, направленная горизонтально назад.
Работа вертикальных сил при горизонтальном движении саней равна нулю, и эти силы нас не интересуют.
Сани движутся равномерно, откуда следует, что горизонтальные силы уравновешивают друг друга. Следовательно, сила тяги F уравновешена силой трения, равной, как известно, произведению коэффициента трения на нормальное давление (36 000 кГ). Подставляя эти данные, найдем
,
Решим теперь эту же задачу в СИ, т. е. примем L в м, M—в кг, T — в сек. Мощность силы, развиваемую тягачом, выразим в ваттах:
N = 80∙736 = 58 880 вт,
скорость —в метрах в секунду:
силу трения выразим в ньютонах:
и, пользуясь формулой (229), получим ответ.
Ответ.
Задача №6
Определение мощности машины можно произвести следующим образом. На вал машины надевают чугунный шкив, который центрируют и закрепляют наглухо зинтами (рис. 215). На шкив надевают две связанные болтами деревянные подушки, одна из которых имеет плечо l с чашкой для грузов Q. Противовес P подбирают так, чтобы свободно надетый на шкив нажим находился в равновесии без гирь Q в горизонтальном положении, т. е. так, чтобы плечо проходило между двумя неподвижными балками А и В. Испытание начинают с того, что затягивают болты подушек до тех пор, пока машина не даст наперед заданное число оборотов n. Коромысло прижимается при этом к неподвижной балке А. Затем начинают накладывать на чашку гири до тех пор, пока плечо не отстанет от А и не займет горизонтальное положение между А и В.
Рис. 215
Определить мощность, если вес гирь известен и равен Q, длина плеча равна l а число оборотов в минуту n. Подобрать длину плеча так, чтобы мощность выражалась формулой N = Qn вт.
Решение. Центр тяжести подушек с противовесом P по условию задачи лежит на одной вертикали с осью шкива На шкив действуют вращающий момент и момент сил трения, сумма которых равна нулю, так как шкив вращается равномерно.
Чтобы определить момент сил трения, рассмотрим равновесие подушки и составим сумму моментов действующих на нее сил относительно оси вала:
Пусть вес выражен в кГ, а длина —в м, тогда для выражения мощности в вт надо эту величину разделить на 0,102 или умножить на 9,81:
Если l = 0,98 м, то N = Qn вт.
Ответ. N = 1,026 Qln вт. Если l = 0,98 м, то N = Qn вт.
Задача №7
Посредством ремня (рис. 216) передается мощность 20 л. с. Радиус ременного шкива 50 см, число оборотов в минуту 150.
Предполагая, что натяжение T1 ведущей ветви вдвое больше натяжения T2 ведомой ветви, определить натяжение T1 и T2.
Решение. Условие задачи дано в технической системе единиц, будем решать в СИ и выражать L — в .и, F — в н, Т —в сек.
Момент натяжения ремня, взятый относительно оси вращения шкива
Мощность 20 л. с. выразим в ваттах.
Натяжение ведущей ветви в два раза больше.
Ответ. T1 = 3750 н; T2= 1875 н. В задачнике И. В. Мещерского ответ дан в кГ, умножая число ньютонов на 0,102, выразим натяжение ремней в килограммах: T2 = 382 κΓ, T1= 191 кГ.
Теоремы об изменении кинетической энергии точки и системы
Изменение кинетической энергии материальной точки равно работе, приложенной к точке силы:
T-T0=A
(127)
Умножим первое из этих уравнений на, второе—на и третье—на . Сокращая dt в знаменателях правых и левых частей, получим:
Сложим все три уравнения и заменим в левой части сумму дифференциалов дифференциалом суммы:
В числителе левой части имеем квадрат полной скорости (64), а правая часть выражает элементарную работу силы (221). Следовательно,
(231)
т. е. дифференциал кинетической энергии равен элементарной работе. Интегрируя равенство (231), получим
Постоянную интеграции определим из начальных данных. В начальное мгновение скорость точки υ = υ0, а работа равнялась нулю. Подставляя эти данные, получим
(232)
Равенство (232) словами можно прочитать так: изменение кинетической энергии материальной точки при перемещении этой точки на каком-либо участке пути равно работе силы, приложенной к точке, на том же участке пути. Уравнение (232) называют уравнением кинетической энергии.
Если на материальную точку действует несколько сил, то А означает работу равнодействующей приложенных к точке сил.
Уравнение (232) можно записать более коротко:
Задача №8
Самолет делает посадку с выключенным мотором на болотистую местность. Какую максимальную горизонтальную скорость v может иметь самолет, не рискуя капотировать (опрокинуться), если расстояние ОС центра тяжести от оси шасси равно с и угол наклона прямой СО с вертикалью в мгновение посадки равняется а (рис. 217).
Рис. 217
Решение. Опрокидывание самолета происходит от того, что при соприкосновении с Землей скорость шасси уменьшается, а корпус продолжает двигаться с постоянной скоростью. Для капота достаточно (и необходимо), чтобы центр тяжести, поднявшись, оказался на вертикали, проходящей через ось шасси.
Так как работа силы тяжести не зависит от траектории центра тяжести, а зависит лишь от его вертикального перемещения, то работа силы тяжести при опрокидывании (рис. 218)
Рис. 218
Вертикальная скорость самолета теряется при ударе о Землю, но горизонтальная сохраняется. Если при спуске самолета шасси остановится, то оставшаяся кинетическая энергия уйдет на опрокидывание самолета:
Решая это уравнение, находим ответ.
Ответ.
Задача №9
Пренебрегая сопротивлением атмосферы, определить, с какой наименьшей скоростью надо бросить материальную точку вертикально вверх, чтобы она не вернулась на Землю.
Решение. Сила, действующая на брошенную с Земли точку, пропорциональна массе точки и обратно пропорциональна квадрату расстояния точки от центра Земли:
Коэффициент пропорциональности был определен при решении задачи № 155:
Материальная точка, получив начальную скорость υ0, будет удаляться от Земли, при этом под действием силы F скорость ее будет уменьшаться, уменьшаться будет и сила F. Материальная точка не вернется на Землю, если в мгновение, когда скорость ее станет равной нулю, перестанет действовать и сила. Сила притяжения обратится в нуль при r = ∞.
Работу силы А при изменении r от R до ∞ выразим интегралом
Знак минус перед интегралом взят потому, что сила направлена в сторону, противоположную движению. Подставляем в (232):
Подставляя числовые данные, получим ответ.
Ответ. (2-я космическая скорость).
Задача №10
В автоматическом оружии отдача используется для выбрасывания пустой гильзы и вкладывания нового патрона. Это осуществляется посредством специального кожуха, сдерживаемого пружиной, который «принимает на себя» отдачу, отскакивает назад и под действием пружины возвращается обратно, производя упомянутые операции. Какова должна быть скорость пули, достаточная для того, чтобы работал автоматический пистолет, если вес пули 8 Г, вес кожуха 250 Г, расстояние, на которое отскакивает кожух, 3 см и сила, необходимая для сжатия пружины на 1 см, равна 4 кГ?
Решение. Путь кожуха 3 см. На этом пути начальная скорость кожуха υ0 уменьшается, достигая нуля. Механическое движение кожуха переходит в упругую энергию пружины. Следовательно, применима теорема об изменении кинетической энергии, пользуясь которой, определим начальную скорость кожуха, так как конечная скорость равна нулю:
Упругая сила пружины изменяется по закону Гука F = cx; подставляя вместо F и х их заданные значения, находим
Подставляя в (221) и интегрируя в пределах от 0 до 3, находим
Работа отрицательна, так как упругая сила пружины направлена против ее деформации и выражена в кГ . см. Выразив в тех же единицах кинетическую энергию кожуха, найдем его начальную скорость:
Итак, после выстрела кожух начал двигаться со скоростью 3,76 м/сек и, пройдя 3 см, остановился, затратив свое механическое движение на сжатие пружины.
После выстрела механическое движение получил не только кожух, но и пуля. Мы не будем больше рассматривать переход механического движения в упругую энергию пружины, а рассмотрим лишь механическое движение кожуха и пули.
Рассмотрим систему, состоящую из пистолета (с кожухом) и пули. Построим оси координат, проведя Ox вдоль дула пистолета. Проекция внешних сил на ось Ox равна нулю. Сила взрыва— внутренняя сила системы и, следовательно, центр масс системы не смещается по оси Ох, и сумма проекций количеств движения после выстрела, как и до выстрела, равна нулю:
откуда скорость пули
Знак минус показывает, что скорость пули направлена в сторону, противоположную скорости кожуха. Если скорость пули будет меньше, будет меньше и количество движения пули, а потому уменьшится и количество движения кожуха. Если же уменьшится количество движения кожуха, то уменьшится и его кинетическая энергия и ее будет недостаточно для совершения работы — сжатия пружины на 3 см, т. е. при меньшей начальной скорости пули пистолет не будет автоматически перезаряжаться. При большей скорости пули избыток кинетической энергии кожуха будет передаваться ударом на руку.
Ответ. υ=120 м/сек.
Изменение кинетической энергии материальной системы равно сумме работ внешних и внутренних сил системы: T-T0 = А
Теорема об изменении кинетической энергии материальной системы
Пусть механическая система состоит из п материальных точек. Разбив на две категории все силы, действующие на точки системы, напишем дифференциальные уравнения в форме (130):
где k = 1, 2, 3, . n.
Рассмотрим отдельно какую-либо из точек системы и напишем для нее уравнение кинетической энергии. На эту точку действуют как внешние, так и внутренние силы, и в правой части уравнения кинетической энергии мы напишем сумму работ внешних и внутренних сил:
Составим такие же уравнения для всех точек и возьмем сумму:
(233)
Припомним, что внутренние силы системы не вошли в уравнения проекций количеств движения системы (169) и в уравнения моментов системы (192). Однако они имеются в уравнении (233) кинетической энергии системы. Происходит это потому, что сумма проекций на любую ось и сумма моментов всех внутренних сил относительно любой оси всегда равны нулю, так как внутренние силы системы попарно равны и действуют по одной прямой в противоположные стороны. Но сумма работ внутренних сил системы в общем случае не равна нулю, как это было показано в задаче № 156.
Пусть, например, две точки системы отталкивают друг друга внутренними равными и противоположно направленными силами и под действием этих сил расстояние между точками увеличивается. Перемещения обеих точек направлены по силам, работы обеих сил положительны, и сумма работ этих сил не равна нулю. Внутренние силы системы можно рассматривать как силы взаимодействия точек, взятых по две. Поэтому сказанное о двух точках распространяется на все точки системы.
Силы взаимодействия между каждыми двумя частицами направлены в противоположные стороны по прямой, соединяющей эти частицы. Если расстояние между частицами не изменяется, то относительное перемещение этих частиц может быть только в направлении, перпендикулярном к этой прямой. Но силы, перпендикулярные к перемещениям, работы не совершают, а потому работа внутренних сил неизменяемой системы (абсолютно твердого тела) равна нулю.
Если система состоит из нескольких твердых тел, то работа внутренних сил каждого твердого тела равна нулю, но работы внутренних сил, действующих между каждыми двумя твердыми телами, принадлежащими к этой системе, в общем случае не равны нулю.
Задача №11
Цилиндрический вал диаметром 10 см и весом 0,5 T, на который насажено маховое колесо диаметром 2 м и весом 3 Т, вращается в данное мгновение с угловой скоростью 60 об/мин, а затем он предоставлен самому себе. Сколько оборотов еще сделает вал до остановки, если коэффициент трения в подшипниках равен 0,05? При решении задачи массу маховика считать равномерно распределенной по его ободу.
Решение. Примем следующие единицы измерения: L-в см, F — в Т, T — в сек.
Требуется определить количество оборотов вала до остановки. Механическое движение (вращение) вала с маховиком исчезает, переходит в другие виды движения. Для решения задачи применим теорему об изменении кинетической энергии (233′).
На вал с насаженным на него маховым колесом действуют силы: 1) вес всей системы, состоящий из веса махового колеса и веса вала, G = 3,5; 2) реакции в опорах; 3) сила трения в подшипниках, равная произведению веса на коэффициент трения; Fτp≈ 0,05-3,5.
Точка приложения первой из этих сил неподвижна, а потому работа первой из этих сил равна нулю.
Реакции перпендикулярны перемещениям, а потому работа реакции равна нулю.
Работу сил трения определим по (226) как работу силы, приложенной к вращающемуся телу. Момент силы трения относительно оси вращения равен произведению силы трения на плечо (на радиус вала):
Работа отрицательна, так как сила направлена против скорости, т. е. если вращение вала происходит против хода часовой стрелки (φ > 0), то Mтp 0, а потому А / )
Если бы существовали абсолютно упругие тела (k = 1), то их соударение происходило бы без потери кинетической энергии, т. е. без нагревания, без звука и пр.
Задача №15
Определить потерю кинетической энергии при прямом центральном ударе двух тел, а также их скорости после удара, если ml = m2 = 2 кг, υ1 =4 м/сек, υ2 =0, k = 0,5.
Решение. Если бы удар был неупругим, то скорость тел после удара была бы по (176):
Учитывая коэффициент восстановления, скорости каждого из тел определим по (178):
Потерю кинетической энергии определим по (236′):
Напомним, что механическое движение имеет две меры: 1) количество движения, т. е. меру, характеризующую способность механического движения передаваться от одних материальных тел к другим в виде механического же движения, и 2) кинетическую энергию, характеризующую способность механического движения переходить в другие немеханические виды движения.
Поэтому кинетическая энергия системы теряется при ударе, переходит в теплоту, звук и пр. и . В данном примере кинетическая энергия системы до удара была , а после удара стала
Потерянная системой двух тел кинетическая энергия 6 кгм 2 /сек 2 перешла в другие немеханические виды движения.
Количество же движения системы лишь передалось от одного тела другому, но сохранилось в системе. В самом деле, K0 = 2∙4 = 8 κг∙м∕ceκ; K = 2∙1 + 2∙3 = 8 κг∙м∕ceκ, т. е. K-K0 = 0.
Ответ. T — T0 = 6 дж; =l м/сек; = 3м/сек.
Коэффициент полезного действия
В этой главе рассмотрены задачи на определение работы, совершаемой постоянной силой, и развиваемой мощности при поступательном и вращательном движении тел.
Работа и мощность при поступательном движении
Работа постоянной силы Р на прямолинейном участке пути s, пройденном точкой приложения силы, определяется по формуле
где a — угол между направлением действия силы и направлением перемещения.
т. e. работа силы, действующей перпендикулярно к направлению перемещения, равна нулю.
Если направление действия силы совпадает с направлением перемещения, то а = 0, поэтому cosa = cos O = 1 и формула (1) упрощается;
На точку или на тело обычно действует не одна сила, а несколько, поэтому при решении задач целесообразно использовать теорему о работе равнодействующей системы сил (Е. М. Н и к ит и и, § 89):
т. е. работа равнодействующей какой-либо системы сил на некотором пути равна алгебраической сумме работ всех сил этой системы на том же пути.
В частном случае, когда система сил уравновешена (тело движется равномерно и прямолинейно), равнодействующая системы сил равна нулю и, следовательно, Поэтому при равномерном и прямолинейном движении точки или тела уравнение (2) принимает вид
т. е. алгебраическая сумма работ уравновешенной системы сил на некотором пути равна нулю.
При этом силы, работа которых положительна, называются движущими, а силы, работа которых отрицательна, называются силами сопротивления. Например, при движении тела вниз—сила тяжести — движущая сила и ее работа положительны, а при движении тела вверх его сила тяжести является силой сопротивления и работа силы тяжести при этом отрицательна (§93, Е. М. Н и к и т и н).
При решении задач в случаях, когда неизвестна сила Р, работу которой нужно определить, можно рекомендовать два приема (метода).
1. При помощи сил, заданных в условии задачи, определить силу Р, а затем по формуле (1) или (1) вычислить ее работу.
2. Не определяя непосредственно силы Р, определить — работу требуемой силы при помощи формул (2) и (2′), выражающих теорему о работе равнодействующей.
Мощность, развиваемая при работе постоянной силы, определяется по формуле
Если при определении работы силы Р скорость движения точки остается постоянной, то
Если же скорость движения точки изменяется, средняя скорость и тогда формула (2′) выпажает среднюю мощность
Коэффициент полезного действия (к. п. д.) при совершении работы можно определить как отношение работ
где — полезная работа; А — вся произведенная работа, или как отношение соответствующих мощностей:
Единицей работы в СИ служит 1 джоуль (дж) =а в системе МКГСС —
Так как единицей длины в обеих системах служит 1 м, а 1 кГ=9,81 н (или 1 н = 0,102 кГ), то
Единицей мощности в СИ служит 1 ватт
а в системе МКГСС—
При использовании системы МКГСС мощность обычно измеряют в лошадиных силах (л. с.), причем
При использовании СИ мощность измеряют в киловаттах (квт): 1 квт — 1,36 л. с.
Для перехода от одних единиц к другим следует пользоваться формулами
Задача №16
Какую работу производит человек, передвигая по горизонтальному полу на расстояние 4 м горизонтально направленным усилием ящик массой 50 кГ? Коэффициент трения f = 0,4.
Решение 1—методом определения движущей силы Р.
1. На ящик, поставленный на горизонтальный пол, действуют две силы: G и реакция пола N (рис. 252). Двигая ящик, че-
ловек прикладывает к нему силу Р, и тогда возникает сила трения F.
При равномерном передвижении ящика четыре силы образуют уравновешенную систему и поэтому, спроектировав их на горизонтальную и вертикальную оси, найдем, что
3. Работа, которую производит человек в данном случае, как видно, состоит в преодолении силы трения (P=F). Но так как
то
4. Если решить задачу в системе МКГСС, то
Легко убедиться, что оба ответа выражают одну и ту же работу:
Решение 2 —с применением теоремы о работе равнодействующей.
1. Как показано в первом решении, на ящик при его перемещении действуют четыре силы: сила тяжести G, реакция пола движущая сила и сила трения F. Ящик движется равномерно и прямолинейно, поэтому эти четыре силы образуют уравновешенную систему. Следовательно, применив формулу (2′). получим уравнение
2. В этом уравнении работа силы тяжести Аа=0, так как сила G действует перпендикулярно к направлению перемещения; по этой же причине работа реакции N
Таким образом, искомая работа при перемещении ящика
3. Работу силы трения найдем по формуле (1), учитывая, что в этом случае а=180°:
Подставим значение в уравнение (а):
Так как F — Nf и N — G, то
AP=Fs — Nfs = Gfs=mgfs
Задача №17
На тело М массой т—40 кг, могущее перемещаться вдоль вертикального направляющего бруска, действует некоторая сила Р, постоянно направленная под углом а =18° к вертикали. Под действием этой силы тело поднимается равномерно на высоту h = 4 м (рис. 253, а); коэффициент трения при скольжении тела вдоль направляющего бруса f=0,2. Определить произведенную работу и коэффициент полезного действия. Решение 1.
1. При равномерном перемещении вдоль бруска вверх на тело М действуют четыре силы: сила тяжести G, сила трения F, нормальная реакция N, равная давлению тела на брусок, и движущая сила Р (рис. 253. б).
2. Сила Р производит работу
Но чтобы определить ее, нужно сначала найти силу Р.
3. Расположив оси координат, как показано на рис. 253, б, выведем уравнения равновесия:
а также уравнение, выражающее основной закон трения:
поэтому уравнение (3) примет вид
Подставим полученное значение силы трения в уравнение (2):
4. Подставим в последнее выражение числовое значение силы тяжести G в единицах СИ (G=mg):
Тогда работа, произведенная силой,
5. Если подставить в уравнение (4) силу тяжести G, выраженную в технических единицах (G = 40 кГ), то
Работа этой силы в единицах МКГСС получит такое значение:
6. Определим коэффициент полезного действия:
Вся произведенная работа А = 1680 дж, а полезная работа состоит в том, что тело весом G — mg поднято на высоту h, т. е.
Умножив найденное значение = 0,934 на 100, выразим к. п. д. в процентах:
Примечание. Можно не определять отдельно числовое значение силы Р виде выражение работы для
(см. п. 4 и 5), а получить предварительно в общем данного случая:
и после деления числителя и знаменателя на cos а:
Но иногда в технических расчетах числовые значения девствующих сил необходимы для решения каких-либо других вопросов.
Если воспользоваться приведенным выше выражением работы, то выражение к. п. д. для данной задачи получит такой вид:
Таким образом, коэффициент полезного действия при передвижении тела М по вертикальному направляющему бруску зависит от коэффициента трения f и угла а, определяющего направление действия силы относительно вертикального бруска.
Если заменить
1. В первом решении выяснено, что на тело М действует система четырех сил: G, F, N, Р (см. рис. 253, б).
2. Так как тело движется по бруску равномерно, система этих сил уравновешена и, следовательно, алгебраическая сумма их работ равна нулю:
3. Тело М движется вертикально вверх и поднимается на высоту h, поэтому работа силы N, направленной перпендикулярно к направлению перемещения:
работа силы тяжести G, направленной вертикально вниз,
работа силы трения F, также направленной вниз,
Известно, что F=Nf. Спроектировав на ось х (см. рис. 253,6) силы, приложенные к телу М, найдем, чтоПоэтомуи выражение работы силы трения примет вид
4. Подставим выражения работ в уравнение (а)
5. Вычислим работу в единицах СИ. Тогда
поэтому
Таким образом, вся работа, произведенная при подъеме тела М на высоту составляет 1670 дж. К. н. д. при выполнении этой работы определяем так же, как и в первом решении.
Задача №18
Какой мощности электродвигатель необходимо поставить на лебедку, чтобы она могла поднимать клеть со строительными материалами общей массой m=1200 кг на высоту 20 м за 30 сек. Коэффициент полезного действия лебедки
Решение (в единицах СИ).
1. Полезная мощность, развиваемая лебедкой при подъеме,
2. Мощность двигателя N найдем из выражения
3 Таким образом, мощность двигателя, необходимая для лебедки,
Двигатель должен иметь мощность не менее 10,9 квот.
Рекомендуется решить самостоятельно эту задачу в единицах МКГСС и найти мощность двигателя, выраженную в л. с.
Задача №19
Какую работу необходимо произвести, чтобы равномерно передвинуть в горизонтальном направлении на расстояние ь клинчатый ползун 1 вдоль направляющих 2? Вес ползуна G, угол заострения ползуна и направляющих а (рис. 254, а), коэффициент трения между ползуном и направляющими f.
1. На клинчатый ползун, когда он находится в горизонтально расположенных направляющих, действуют три силы: вес ползуна и две реакции направляющих (рис. 254, в), действующих на ползун перпендикулярно к боковым плоскостям (щекам) ползуна.
Для приведения ползуна в движение к нему нужно приложить параллельно направляющим силу и тогда возникнут еще две силы — силы трения, действующие вдоль обеих боковых плоскостей ползуна (см. рис. 254, б — здесь вектор изображает направленную вертикально вверх геометрическую сумму нормальных реакций
Таким образом, на ползун при его движении действуют всего шесть сил:
В данном случае нормальные реакции равны между собой, следовательно, равны и силы трения поэтому
2. Работа при перемещении ползуна на расстояние s
но предварительно найдем числовое значение движущей силы Р.
3. Спроектировав приложенные к ползуну силы на ось х
(см. рис. 254, б), получим
Нормальную реакцию N найдем из уравнения проекций на ось у (см. рис. 254, в):
Подставляем найденное значение N в
4. Следовательно, работа при передвижении клинчатого ползуна на расстояние s
Например, при
Примечание. Входящая в формулу (б) величина называется коэффициентом трения клинчатого ползуна. При уменьшении угла а (при большем
заострении ползуна и направляющих) коэффициент трения клинчатого ползуна резко увеличивается.
Решение задачи вторым способом с применением теоремы о работе равнодействующей силы рекомендуется выполнить самостоятельно.
Задача №20
Тело М весом G = 50 кГ равномерно перемещается вверх по наклонной плоскости, длина которой м и угол подъема а = 20; (рис. 255, а). Определить работу, производимую силой, направленной параллельно наклонной плоскости, и коэффициент полезного действия наклонной плоскости. Коэффициент трения f=0,2. Решение 1.
1. При движении тела М (примем его за материальную точку) вверх по наклонной плоскости на него действуют четыре силы: вес нормальная реакция наклонной плоскости движущая сила и сила трения (рис. 255, б).
2. Работа силы Р при перемещении тела по длине наклонной плоскости
3. Найдем необходимую для перемещения тела М силу Р. Расположив оси координат, как показано на рис. 255, 6, составим два уравнения равновесия:
Дополним эти уравнения третьим уравнением, выражающим основной закон трения:
Вместо силы трения F подставим ее значение из уравнения (3):
а вместо нормальной реакции N подставим ее значение из уравнения (2):
4. Следовательно, работа силы P
После подстановки в это уравнение числовых значений
5. Находим к. п. д. наклонной плоскости:
Полезная работа состоит в подъеме тела весом G на высоту поэтому
Решение 2.
1. Можно считать, что на тело М действуют не четыре, а три силы: G—вес тела, движущая сила и полная реакция поверхности реальной связи R, равная геометрической сумме сил(рис. 255, в).
Реакция реальной связи R, как известно (§ 15-3), при движении отклоняется от нормали к поверхности связи на величину угла трения причем — коэффициент трения.
2. Так как на тело М действуют только три силы и они образуют уравновешенную систему (тело М, принятое за материальную точку, движется равномерно и прямолинейно), силовой треугольник АВС, построенный из этих сил, является замкнутым.
3. По рис. 255, в можно определить, что в силовом треугольнике AВС угол Следовательно,
4. Применим к АВС теорему синусов’
5. Работа силы Р
Из равенства (см. п. 1) находим, чтоПодставим теперь в выражение работы числовые значения и определим, что
6. Находим к. п. д. наклонной плоскости:
Развернем знаменатель получившейся дроби:
Числитель и знаменатель разделим на произведение и получим окончательный вид формулы к. п. д. наклонной плоскости при действии силы Р, параллельной этой плоскости
Подставив сюда значение углаи учтя, что получим
Примечания: I. Как видно, результаты обоих решений совпадают, хотя получившиеся формулы для силы Р внешне отличаются друг от друга.
Формулу для Р из первого решения легко преобразовать и привести к результату второго решения:
2. Выражение (I), полученное во втором решении, показывает, что к. п. д. наклонной плоскости зависит лишь от коэффициента треният. е. от материала и состояния трущихся поверхностей тела М и угла подъема наклонной плоскости.
1. Известно, что при действии на точку нескольких сил алгебраическая сумма работ всех сил на некотором пути равна работе равнодействующих этих сил.
2. В данном случае на тело М, которое примем за материальную точку, действуют четыре силы: вес нормальная реакция наклонной плоскости сила трения и движущая сила Р (см. рис 255, б).
3. Точка М движется равномерно и прямолинейно. Равнодействующая сил, действующих на точку, равна нулю, и, следовательно, алгебраическая сумма работ, производимых силами на длине наклонной плоскости, также равна нулю:
4. Находим отсюда работу силы Р:
где работа силы
работа силы направленной перпендикулярно к направлению движения точки, равна нулю:
так как сила трения
Подставим в выражение (а) полученные значения работ:
5. К п. д. наклонной плоскости найдем так же, как в п 5 первого решения.
Задача №21
Тело М весом G = 50 кГ равномерно перемещается вверх по наклонной плоскостимне углом подъема
а=20 . Определить работу, произведенную силой, направленной параллельно основанию наклонной плоскости (рис. 256, а), также коэффициент полезного действия наклонной плоскости. Коэффициент трения f = 0,4.
Первое и третье решения задачи, аналогичные соответствующим решениям задачи 225-44, рекомендуется выполнить самостоятельно.
1. Приняв тело М за материальную точку, изобразим на рис. 256, б (слева) три действующие на нее силы: вес G, движущую силу Р и полную реакцию R наклонной плоскости, которая отклонена на угол (угол трения) от нормали к поверхности наклонной плоскости.
2. При равномерном движении тела по наклонной плоскости эти три силы образуют уравновешенную систему, и поэтому треугольник АВС, построенный из этих сил, является замкнутым (см. рис. 256, б — справа).
3. Силовой треугольник АВС получается в данном случае прямоугольным, так как вектор G перпендикулярен к вектору Р; угол поэтому числовое значение движущей силы
* Работа силы P в результате вычислений получается отрицательной, так как плоскость несамотормозящаяся (угол подъема а угол трения следовательно, см. задачу 95-15) и поэтому сила Р направлена вверх, т. е. в сторону, противоположную движению. Без силы Р тело M скользит вниз равноускоренно.
5. Подставим сюда числовые значения:Найдем
Как видно, по сравнению с задачей 225-44 работа получается несколько больше (на 24 кГм), потому что сила Р, действующая параллельно основанию наклонной плоскости, прижимает тело к наклонной плоскости, при этом увеличивается нормальное давление тела N, а вместе с ним и сила трения.
G. Определим коэффициент полезного действия. На основании изложенного, к. п. д. в данном случае уменьшится:
окончательно получаем формулу к. п. д. горизонтальном действии силы Р:
Подставим сюда значения углов:
По сравнению с к. п. д., полученным в задаче 225-44, к. п. д. наклонной плоскости в этой задаче уменьшается.
Следующую задачу рекомендуется решить самостоятельно.
Задача №22
Определить работу, которую необходимо произвести, чтобы перекатить каток массой 50 кГ на расстояние 4 м по горизонтальной негладкой поверхности. Считать, что сила, двигающая каток, приложена к оси катка и горизонтальна (рис. 258, а).
Диаметр катка 20 см; коэффициент трения = 0,5 см.
1. Как известно из кинематики, движение катящегося катка называется плоскопараллельным и составляется из двух движений — поступательного и вращательного.
Ось катка передвигается поступательно, поэтому работу силы Р, приложенной к оси, можно определить по формуле
но предварительно нужно найти числовое значение силы Р.
2. На каток в неподвижном состоянии действуют две силы: вес катка G и реакция N горизонтальной поверхности, приложенная к катку в точке К (геометрическая точка касания катка с поверхностью). При качении на Каток действуют уже четыре силы (рис. 258, б): G — вес катка, Р -движущая сила и две составляющие N и F полной реакции поверхности, место приложения которой перемещается из точки К в точку А — вперед по ходу катка.
3. Если спроектировать все силы на вертикальную и горизонтальную оси, то N — G и Р = Р, т. е. на катящийся каток действуют две пары сил: катящая пара (Р; F) с плечом ОКи пара сопротивления (G; N) с плечом КА =
При равномерном перекатывании катка моменты этих пар численно равны между собой, т. е.
Отсюда находим силу Р, выразив силу тяжести в кГ (G — = 50 кГ)
4. Таким образом, работа, произведенная при перемещении катка,
Рекомендуется сопоставить этот результат с результатом, полученным в задаче 221-44. Следующую задачу решить самостоятельно.
Работа и мощность при вращательном движении
При вращательном движении тела движущим фактором является пара сил. Рассмотрим диск 1, могущий свободно вращаться вокруг оси 2 (рис. 259). Если к точке А на ободе диска приложить силу Р (направим ее вдоль касательной к боковой поверхности диска; направленная таким образом сила называется окружным усилием), то диск станет вращаться. Вращение диска обусловлено появлением пары сил. Сила Р, действуя на диск, прижимает его в точке О к оси (сила на рис. 259, приложенная к оси 2) и возникает реакция оси (сила на рис. 259), приложенная так же, как и сила Р, к диску. Так как все эти силы численно равны между собой и_ линии их действия параллельны, то силы Р и образуют пару сил, которая и приводит диск во вращение.
Как известно, вращающее действие пары сил измеряется ее моментом, но момент пары сил равен произведению модуля любой из сил на плечо пары, поэтому вращающий момент
Единицей момента пары сил, а также момента силы относительно точки или относительно оси является (ньютон-метр) в СИ и 1 кГм (килограмм-сила-метр) в системе МКГСС. Но при этом не следует смешивать эти единицы с единицами работы имеющими ту же размерность.
Работу при вращательном движении производят пары сил. Величина работы пары сил измеряется произведением момента пары (вращающего момента) на угол поворота, выраженный в радианах:
Таким образом, чтобы получить единицу работы, например, необходимо единицу моментаумножить на 1 рад. Но так как радиан — безразмерная величина
Мощность при вращательном движении
Если тело вращается с постоянной угловой скоростью, то, заменив в формуле (2) получим
Мощность того или иного двигателя величина постоянная, поэтому
т. е. вращающий момент двигателя обратно пропорционален угловой скорости его вала.
Это означает, что использование мощности двигателя при различных угловых скоростях позволяет изменять создаваемый им вращающий момент. Используя мощность двигателя при малой угловой скорости, можно получить большой вращающий момент.
Так как угловая скорость вращающейся части двигателя (ротора электродвигателя, коленчатого вала двигателя внутреннего сгорания и т. п.) при его работе практически нс изменяется, то между двигателем и рабочей машиной устанавливается какой-либо механизм (редуктор, коробка скоростей и т. н.), могущий передавать мощность двигателя при различных угловых скоростях.
Поэтому формула (3), выражающая зависимость вращающего момента от передаваемой мощности и угловой скорости (Е. М. Н и-китнн, § 93), имеет очень важное значение.
Используя при решении задач эту зависимость, необходимо иметь в виду следующее. Формула (3) принимается для решения задач, если мощность N задана в ваттах, а угловая скорость—в рад/сек [размерность (1/сек)], тогда вращающий момент получится в н м.
Соответственно, если мощность N подставлена в кет (киловаттах), то вращающий момент получится в к-нм (килоньютон-метрах).
Если передаваемая мощность выражена в л. с. (1 л. с. =
= 75угловая скорость — в об;мин
а вращающий момент нужно получить в кГм, то необходимо воспользоваться формулой
Если передаваемая мощность выражена в кет, угловая скорость — в об/мин, а вращающий момент нужно получить в кГ м, то необходимо воспользоваться формулой
Задача №23
Для определения мощности электродвигателя через его шкив перекинута тормозная лента (рис. 260, а). Один конец ленты удерживается динамометром, а к другому концу прикрепленадвухкилограммовая гиря.
После запуска двигателя при установившейся угловой скорости n = 1850 об/мин динамометр показывает усилие 5 кГ. Определить мощность двигателя.
Решение 1—в единицах СИ.
1. Рассмотрим, какие силы действуют на шкив при установившемся равномерном вращении.
Шкив приводится во вращательное движение вращающим моментом создаваемым двигателем. Кроме того, на шкив действуют сила натяжения правой ветви ленты, создаваемая динамометром и сила натяжения левой ветви ленты, создаваемая двухкилограммовой гирей (рис. 260,6).
2. Определим вращающий момент двигателя.
Так как шкив вращается равномерно, то алгебраическая сумма моментов всех сил относительно оси вращения шкива равна нулю:
3. Переведя угловую скорость n =1850 об/мин в рид/сек:
из формулы (3) можно найти мощность двигателя!
Таким образом, мощность двигателя составляет 685 вт. Решение 2 —при помощи формулы (4).
1. На шкив действуют — искомый вращающий момент двигателя и две силы натяжения ветвей тормозной ленты: и
2. Определяем вращающий момент двигателя:
3. Теперь из формулы (4) определяем мощность двигателя:
Переведя получившуюся мощность из л. с. в вт, легко убедиться, что она такая же, как и в первом решении (0,930 л. с
Задачу можно решить еще при помощи формулы (5). Рекомендуется это решение выполнить самостоятельно.
Задача №24
Токарный станок приводится в движение электродвигателем, мощность которого N = 2,21 кет. Считая, что к резцу станка подводится лишь 0,8 мощности двигателя, определить вертикальную составляющую усилия резания, если диаметр обрабатываемой детали d = 200 мм, а шпиндель вращается со скоростью n=92 об/мин.
Решение — при помощи формулы (5).
1. Шпиндель станка с закрепленной в нем деталью вращается под действием вращающего момента, который уравновешивается моментом искомого вертикального усилия резания Р, т. е.
где d—200 лш = 0,2 м — диаметр обрабатываемой детали. Следовательно,
2. Мощность, подведенная к резцу, составляет 0,8 от всей мощности двигателя. Таким образом, к. п. д. передачи и подведенная к резцу мощность
3. Подставим найденные значения и данное в условии задачи значение n в формулу (5):
Решение задачи в единицах СИ рекомендуется выполнить самостоятельно.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Потенциальная энергия
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие
- Основные законы динамики
- Колебания материальной точки
- Количество движения
- Момент количества движения
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Техническая механика
Работа, мощность, энергия
Работа постоянной силы на прямолинейном участке
Рассмотрим материальную точку М , к которой приложена сила F . Пусть точка переместилась из положения М0 в положение М1 , пройдя путь s (рис. 1) .
Чтобы установить количественную меру воздействия силы F на пути s , разложим эту силу на составляющие N и R , направленные соответственно перпендикулярно направлению перемещения и вдоль него. Так как составляющая N (перпендикулярная перемещению) не может двигать точку или сопротивляться ее перемещению в направлении s , то действие силы F на пути s можно определить произведением Rs .
Эта величина называется работой и обозначается W .
Следовательно,
W = Rs = Fs cos α ,
т. е. работа силы равна произведению ее модуля на путь и на косинус угла между направлением вектора силы и направлением перемещения материальной точки.
Таким образом, работа является мерой действия силы, приложенной к материальной точке при некотором ее перемещении .
Работа является скалярной величиной.
Рассматривая работу силы, можно выделить три частных случая: сила направлена вдоль перемещения (α = 0˚) , сила направлена в противоположном перемещению направлении (α = 180˚) , и сила перпендикулярна перемещению (α = 90˚) .
Исходя из величины косинуса угла α , можно сделать вывод, что в первом случае работа будет положительной, во втором – отрицательной, а в третьем случае (cos 90˚ = 0) работа силы равна нулю.
Так, например, при движении тела вниз работа силы тяжести будет положительной (вектор силы совпадает с перемещением), при подъеме тела вверх работа силы тяжести будет отрицательной, а при горизонтальном перемещении тела относительно поверхности Земли работа силы тяжести будет равна нулю.
Силы, совершающие положительную работу, называются движущимися силами , силы, а совершающие отрицательную работу – силами сопротивления .
Единицей работы принят джоуль (Дж):
1 Дж = сила×длина = ньютон×метр = 1 Нм.
Джоуль – это работа силы в один ньютон на пути в один метр.
Работа силы на криволинейном участке пути
На бесконечно малом участке ds криволинейный путь можно условно считать прямолинейным, а силу – постоянной.
Тогда элементарная работа dW силы на пути ds равна
dW = F ds cos (F , v) .
Работа на конечном перемещении равна сумме элементарных работ:
W = ∫ F cos (F , v) ds .
На рисунке 2а изображен график зависимости между пройденным расстоянием и F cos (F , v) . Площадь заштрихованной полоски, которую при бесконечно малом перемещении ds можно принять за прямоугольник, равна элементарной работе на пути ds :
dW = F cos (F , v) ds ,
а работа силы F на конечном пути s графически выражается площадью фигуры ОАВС , ограниченной осью абсцисс, двумя ординатами и кривой АВ , которая называется кривой сил .
Если работа совпадает с направлением перемещения и возрастает от нуля пропорционально пути, то работа графически выражается площадью треугольника ОАВ (рис. 2 б) , которая, как известно, может быть определена половиной произведения основания на высоту, т. е. половиной произведения силы на путь:
Теорема о работе равнодействующей
Теорема: работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том же участке пути .
Пусть к материальной точке М приложена система сил (F1 , F2 , F3 . Fn) , равнодействующая которых равна FΣ (рис. 3) .
Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно,
Спроецируем это векторное равенство на касательную к траектории, по которой движется материальная точка, тогда:
Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем полученное равенство в пределах какого-то конечного перемещения s :
что соответствует равенству:
Теорема о работе силы тяжести
Теорема: работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения .
Пусть материальная точка М движется под действием силы тяжести G и за какой-то промежуток времени перемещается из положения М1 в положение М2 , пройдя путь s (рис. 4) .
На траектории точки М выделим бесконечно малый участок ds , который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна.
Из заштрихованного треугольника получим, что
Элементарная работа силы G на пути ds равна:
Полная работа силы тяжести G на пути s равна
W = ∫ Gds cos α = ∫ Gdy = G ∫ dy = Gh .
Итак, работа силы тяжести равна произведению силы на вертикальное перемещение точки ее приложения:
Пример решения задачи по определению работы силы тяжести
Задача: Однородный прямоугольный массив АВСD массой m = 4080 кг имеет размеры, указанные на рис. 5 .
Определить работу, которую необходимо выполнить для опрокидывания массива вокруг ребра D .
Решение.
Очевидно, что искомая работа будет равна работе сопротивления, совершаемой силой тяжести массива, при этом вертикальное перемещение центра тяжести массива при опрокидывании через ребро D является путем, который определяет величину работы силы тяжести.
Для начала определим силу тяжести массива: G = mg = 4080×9,81 = 40 000 Н = 40 кН .
Для определения вертикального перемещения h центра тяжести прямоугольного однородного массива (он находится в точке пересечения диагоналей прямоугольника), используем теорему Пифагора, исходя из которой:
КО1 = ОD – КD = √(ОК 2 + КD 2 ) – КD = √(3 2 +4 2 ) — 4 = 1 м .
На основании теоремы о работе силы тяжести определим искомую работу, необходимую для опрокидывания массива:
W = G×КО1 = 40 000×1 = 40 000 Дж = 40 кДж.
Работа постоянной силы, приложенной к вращающемуся телу
Представим себе диск, вращающийся вокруг неподвижной оси под действием постоянной силы F (рис. 6) , точка приложения которой перемещается вместе с диском. Разложим силу F на три взаимно-перпендикулярные составляющие: F1 – окружная сила, F2 – осевая сила, F3 – радиальная сила.
При повороте диска на бесконечно малый угол dφ сила F совершит элементарную работу, которая на основании теоремы о работе равнодействующей будет равна сумме работ составляющих.
Очевидно, что работа составляющих F2 и F3 будет равна нулю, так как векторы этих сил перпендикулярны бесконечно малому перемещению ds точки приложения М , поэтому элементарная работа силы F равна работе ее составляющей F1 :
При повороте диска на конечный угол φ работа силы F равна
где угол φ выражается в радианах.
Так как моменты составляющих F2 и F3 относительно оси z равны нулю, то на основании теоремы Вариньона момент силы F относительно оси z равен:
Момент силы, приложенной к диску, относительно оси вращения называется вращающим моментом, и, согласно стандарту ИСО, обозначается буквой Т :
Т = Мz(F) , следовательно, W = Tφ .
Работа постоянной силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угловое перемещение .
Пример решения задачи
Задача: рабочий вращает рукоятку лебедки силой F = 200 Н , перпендикулярной радиусу вращения.
Найти работу, затраченную в течение времени t = 25 секунд , если длина рукоятки r = 0,4 м , а ее угловая скорость ω = π/3 рад/с .
Решение.
Прежде всего определим угловое перемещение φ рукоятки лебедки за 25 секунд :
φ = ωt = (π/3)×25 = 26,18 рад.
Далее воспользуемся формулой для определения работы силы при вращательном движении:
W = Tφ = Frφ = 200×0,4×26,18 ≈ 2100 Дж ≈ 2,1 кДж .
Мощность
Работа, совершаемая какой-либо силой, может быть за различные промежутки времени, т. е. с разной скоростью. Чтобы охарактеризовать, насколько быстро совершается работа, в механике существует понятие мощности , которую обычно обозначают буквой P .
Мощностью называется работа, совершаемая в единицу времени.
Если работа совершается равномерно, то мощность определяют по формуле
Если направление силы и направление перемещения совпадают, что эту формулу можно записать в иной форме:
P = W/t = Fs/t или P = Fv .
Мощность силы равна произведению модуля силы на скорость точки ее приложения .
Если работа совершается силой, приложенной к равномерно вращающемуся телу, то мощность в этом случае может быть определена по формуле:
P = W/t = Tφ/t или P = Tω .
Мощность силы, приложенной к равномерно вращающемуся телу, равна произведению вращающего момента на угловую скорость .
Единицей измерения мощности является ватт (Вт):
Ватт = работа/время = джоуль в секунду.
Понятие об энергии и КПД
Способность тела при переходе из одного состояния в другое совершать работу называется энергией . Энергия есть общая мера различных форм движения материи.
В механике для передачи и преобразования энергии применяются различные механизмы и машины, назначение которых – выполнение заданных человеком полезных функций. При этом энергия, передаваемая механизмами, называется механической энергией , которая принципиально отличается от тепловой, электрической, электромагнитной, ядерной и других известных видов энергии. Виды механической энергии тела мы рассмотрим на следующей странице, а здесь лишь определимся с основными понятиями и определениями.
При передаче или преобразовании энергии, а также при совершении работы, имеют место потери энергии, поскольку механизмы и машины, служащие для передачи или преобразования энергии преодолевают различные силы сопротивления (трения, сопротивления окружающей среды и т. п.). По этой причине часть энергии при передаче безвозвратно теряется и не может быть использована для выполнения полезной работы.
Коэффициент полезного действия
Часть энергии, потерянная при ее передаче на преодоление сил сопротивления, учитывается при помощи коэффициента полезного действия механизма (машины), передающего эту энергию.
Коэффициент полезного действия (КПД) обозначается буквой η и определяется, как отношение полезной работы (или мощности) к затраченной:
Если коэффициент полезного действия учитывает только механические потери, то его называют механическим КПД.
Очевидно, что КПД – всегда правильная дробь (иногда его выражают в процентах) и его значение не может быть больше единицы. Чем ближе значение КПД к единице (100 %) , тем экономичнее работает машина.
Если энергия или мощность передаются рядом последовательных механизмов, то суммарный КПД может быть определен, как произведение КПД всех механизмов:
где: η1 , η2 , η3 , . ηn – КПД каждого механизма в отдельности.
http://www.evkova.org/moschnost-i-rabota-silyi-v-teoreticheskoj-mehanike
http://k-a-t.ru/tex_mex/22-dinamika_5/
Назначение. Онлайн калькулятор предназначен для нахождения работы силы F при перемещении вдоль дуги линии L.
- Решение онлайн
- Видеоинструкция
Криволинейные и поверхностные интегралы второго рода
Рассмотрим многообразие σ. Пусть τ(x,y,z)— единичный вектор касательной к σ, если σ — кривая, а n(x,y,z)— единичный вектор нормали к σ, если σ — поверхность в R3. Введём векторы dl=τ·dl и dS=n·dS, где dl и dS — длина и площадь соответствующего участка кривой или поверхности. Будем считать, что dσ=dl, если σ — кривая, и dσ=dS, если σ — поверхность. Назовём dσ ориентированной мерой соответствующего участка кривой или поверхности.
Определение. Пусть заданы ориентированное непрерывное кусочно-гладкое многообразие σ и на σ – вектор-функция F(x,y,z)=P(x,y,z)i+Q(x,y,z)+R(x,y,z). Разобьем многообразие на части многообразиями меньшей размерности (кривую – точками, поверхность –кривыми), внутри каждого полученного элементарного многообразия выберем по точке M0(x0,y0,z0), M1(x1,y1,z1), … ,Mn(xn,yn,zn). Посчитаем значения F(xi,yi,zi), i=1,2,…,n вектор-функции в этих точках,умножим скалярно эти значения на ориентированную меру dσi данного элементарного многообразия (ориентированные длину или площадь соответствующего участка многообразия) и просуммируем. Предел полученных сумм если онсуществует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если σ -кривая и поверхностным, если σ — поверхность) второго рода, интеграломвдоль ориентированного многообразия, или интегралом от вектора F вдоль σ, и обозначается в общем случае
, в случаях криволинейного и поверхностного интегралов
соответственно.
Заметим, что если F(x,y,z) — сила, то — работа этой силы по перемещению материальной точки вдоль кривой, если F(x,y,z) — стационарное (не зависящее от времени) поле скоростей текущей жидкости, то
— количество жидкости, протекающей через поверхность S в единицу времени (поток вектора через поверхность).
Если кривая задана параметрически 
то
и для криволинейного интеграла второго рода имеем
Так как dS=n·dS=(cosα, cosβ, cosγ), где cosα, cosβ, cosγ — направляющие косинусы единичного вектора нормали n и cosαdS=dydz, cosβdS=dxdz, cosγdS=dxdy, то для поверхностного интеграла второго рода получаем
Если поверхность задана параметрически 
r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k, (u,v)∈D
то
где 
соответственно.
Если поверхность S может быть задана одновременно уравнениями то поверхностный интеграл второго рода вычисляется по формуле
где D1, D2, D3 — проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно и знак “+” берётся, если угол между вектором нормали и осью, вдоль которой ведётся проектирование, острый, а знак “–“, если этот угол тупой.
Свойства криволинейного и поверхностного интегралов второго рода
Отметим некоторые свойства криволинейного и поверхностного интегралов второго рода.
Теорема 1. Криволинейный и поверхностный интегралы 2-го рода зависят от ориентации кривой и поверхности, точнее
.
Теорема 2. Пусть σ=σ1∪σ2 и размерность пересечения dlim(σ1∩σ2)=n-1. Тогда
Доказательство. Включив в число многообразий разбиения в определении интеграла по многообразию второго рода общую границу σ1 с σ2 получаем требуемое.
Пример №1. Найти работу силы F при перемещении вдоль дуги линии L от точки M0 до точки M1.
F=x2yi+yj;, L: отрезок M0M1
M0(-1;3), M0(0;1)
Решение.
Находим уравнение прямой вдоль отрезка M0M1.
или
y=-2x+1
dy=-2dx
Пределы изменения x: [-1; 0]
Пример №2. Вычислить вдоль кривой
, если t∈[0;π]
Имеем
Пример №3. Вычислить поток вектора f(x,y,z)=(yz,xz,xy)T через часть плоскости x+y+z=a лежащую в первом октанте.
Поток вектора через поверхность равен поверхностному интегралу второго рода Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
где S1, S2, S3 — проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно. Посчитаем первый из них. Имеем 
Поэтому поток вектора через поверхность равен
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Поэтому поток вектора через поверхность равен
Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями.
На материальную точку $Tleft(x,yright)$ действует переменная сила $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$. Под действием этой силы материальная точка перемещается на отрезке $left[6;15right]$ от точки $M$ до точки $N$ вдоль синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$. Найти работу переменной силы $overline{F}$ на криволинейном пути от точки $M$ до точки $N$. Построить графическое изображение пути от точки $M$ до точки $N$, а также векторы переменной сили $overline{F}$ в этих точках.
Выполняем графическое изображение синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$ на отрезке $left[6;15right]$.
Находим значения синусоиды в точках $x_{M} =6$ и $x_{N} =15$:
- $y_{M} =7cdot sin left(0,31cdot 6-1,57right)+2approx 4$;
- $y_{N} =7cdot sin left(0,31cdot 15-1,57right)+2approx 2,43$.
Выполняем графические изображения векторов переменной силы $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$, значения которого в точках $M$ и $N$ соответственно равны $overline{F}_{M} =left(3cdot 6-2cdot 4right)cdot overline{i}+4cdot 4cdot overline{j}=10cdot overline{i}+16cdot overline{j}$ и $bar{F}_{N} =left(3cdot 15-2cdot 2,43right)cdot overline{i}+4cdot 2,43cdot overline{j}=40,14cdot overline{i}+9,72cdot overline{j}$.
Работу данной силы на данном участке кривой $MN$ вычисляем по формуле $A=int limits _{a}^{b}Pleft(x,yleft(xright)right)cdot dx +int limits _{a}^{b}Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
Здесь участок кривой $MN$ задан на отрезке $left[x_{M} ,; x_{N} right]$, поэтому формула для работы приобретает вид: $A=int limits _{x_{M} }^{x_{N} }Pleft(x,yleft(xright)right)cdot dx +int limits _{x_{M} }^{x_{N} }Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
В этой формуле первый интеграл дает значение работы силы $F$ вдоль оси $Ox$, второй интеграл — вдоль оси $Oy$.
Находим работу силы вдоль оси $Ox$: $A_{x} =int limits _{6}^{15}Pleft(x,yleft(xright)right)cdot dx $.
Согласно условию задачи имеем:
[Pleft(x,yright)=3cdot x-2cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2.]
Поэтому:
[Pleft(x,yleft(xright)right)=3cdot x-2cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=]
[=3cdot x-14cdot sin left(0,31cdot x-1,57right)-4.]
Далее получаем:
[A_{x} =int limits _{6}^{15}left(3cdot x-14cdot sin left(0,31cdot x-1,57right)-4right)cdot dx =]
[=int limits _{6}^{15}3cdot xcdot dx +int limits _{6}^{15}left(-14cdot sin left(0,31cdot x-1,57right)right)cdot dx +int limits _{6}^{15}left(-4right)cdot dx =]
[=3cdot int limits _{6}^{15}xcdot dx -14cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dx -4cdot int limits _{6}^{15}dx =]
[=3cdot left[frac{x^{2} }{2} right]_{6}^{15} -14cdot left[-frac{1}{0,31} cdot cos left(0,31cdot x-1,57right)right]_{6}^{15} -4cdot left[xright]_{6}^{15} =]
[=1,5cdot left(15^{2} -6^{2} right)+frac{14}{0,31} cdot left(cos left(0,31cdot 15-1,57right)-cos left(0,31cdot 6-1,57right)right)-]
[-4cdot left(15-6right)=135,15.]
Находим работу силы вдоль оси $Oy$: $A_{y} =int limits _{6}^{15}Qleft(x,yleft(xright)right)cdot y’cdot dx $.
Согласно условию задачи имеем:
[Qleft(x,yright)=4cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2. ]
Поэтому:
[Qleft(x,yleft(xright)right)=4cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=28cdot sin left(0,31cdot x-1,57right)+8;]
[y’=7cdot 0,31cdot cos left(0,31cdot x-1,57right)=2,17cdot cos left(0,31cdot x-1,57right).]
Далее получаем:
[A_{y} =int limits _{6}^{15}left(28cdot sin left(0,31cdot x-1,57right)+8right)cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}28cdot 2,17cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}8cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}60,76cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}17,36cdot cos left(0,31cdot x-1,57right)cdot dx .]
Вычисляем первый интеграл $I_{1} $:
[I_{1} =60,76cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=60,76cdot frac{1}{0,31} cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dleft(sin left(0,31cdot x-1,57right)right) =]
[=196cdot left[frac{sin ^{2} left(0,31cdot x-1,57right)}{2} right]_{6}^{15} =]
[=98cdot left(sin ^{2} left(0,31cdot 15-1,57right)-sin ^{2} left(0,31cdot 6-1,57right)right)approx -7,64.]
Вычисляем второй интеграл $I_{2} $:
[I_{2} =17,36cdot int limits _{6}^{15}cos left(0,31cdot x-1,57right)cdot dx =]
[=17,36cdot frac{1}{0,31} cdot left[sin left(0,31cdot x-1,57right)right]_{6}^{15} =]
[=56cdot left(sin left(0,31cdot 15-1,57right)-sin left(0,31cdot 6-1,57right)right)approx -12,57.]
Работа силы вдоль оси $Oy$:
[A_{y} =I_{1} +I_{2} =-7,64-12,57=-20,21.]
Общая работа силы при перемещении вдоль кривой:
[A=A_{x} +A_{y} =135,15-20,21=114,94.]