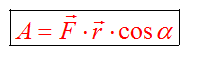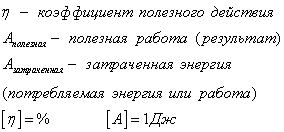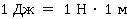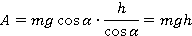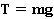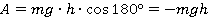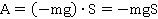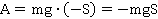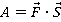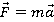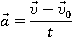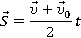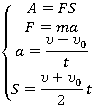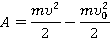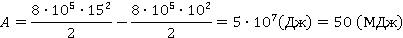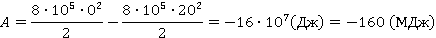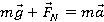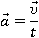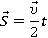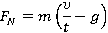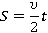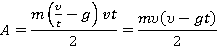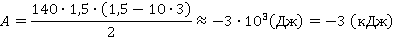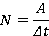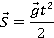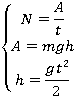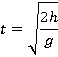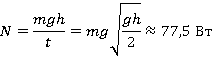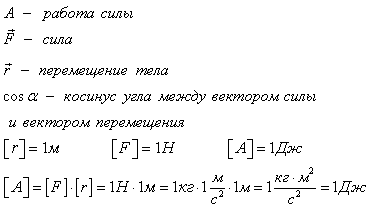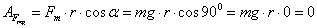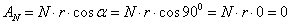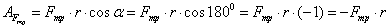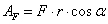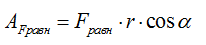I. Механика
Тестирование онлайн
Работа
Работа — это скалярная величина, которая определяется по формуле
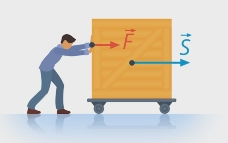
Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение.
Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.
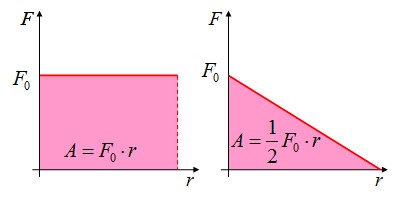
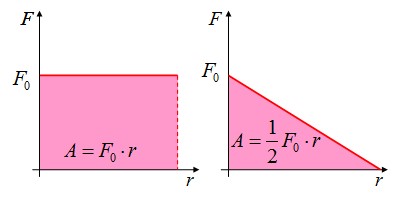
Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.
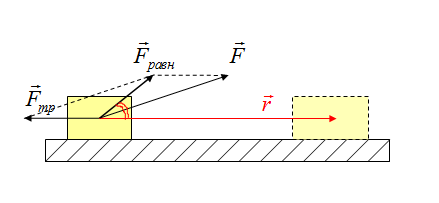
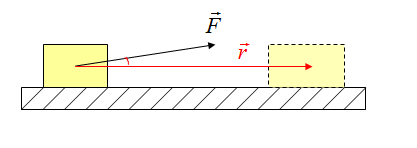
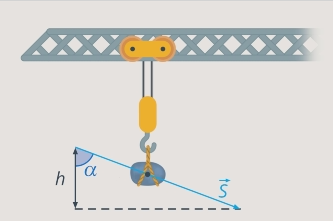
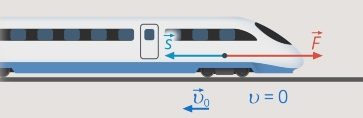
Угол между вектором силы и перемещением
1) Верно определяем направление силы, которая выполняет работу; 2) Изображаем вектор перемещения; 3) Переносим вектора в одну точку, получаем искомый угол.
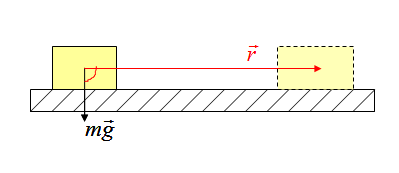
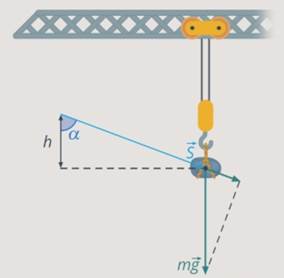
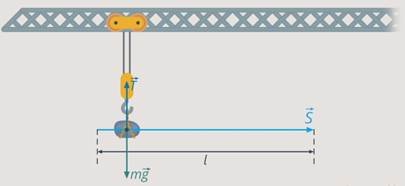
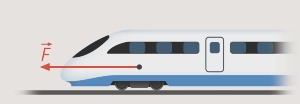
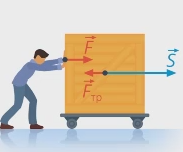
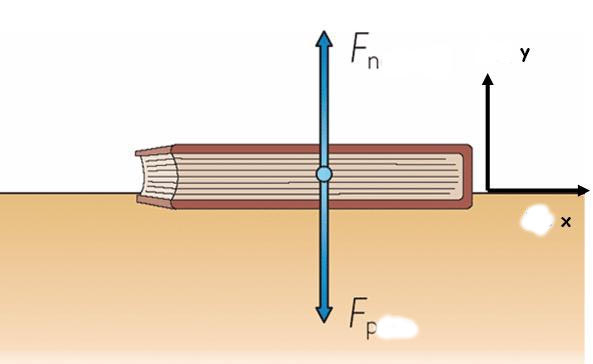
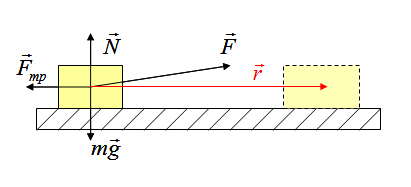
На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r.
Работа силы тяжести
Работа реакции опоры
Работа силы трения
Работа силы натяжения веревки
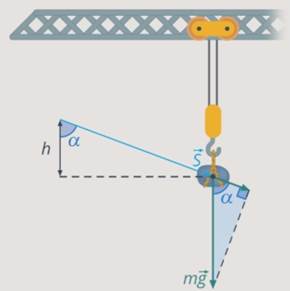
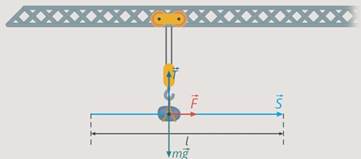
Работа равнодействующей силы
Работу равнодействующей силы можно найти двумя способами: 1 способ — как сумму работ (с учетом знаков «+» или «-«) всех действующих на тело сил, в нашем примере 
2 способ — в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок

Работа силы упругости
Для нахождения работы, совершенной силой упругости, необходимо учесть, что эта сила изменяется, так как зависит от удлинения пружины. Из закона Гука следует, что при увеличении абсолютного удлинения, сила увеличивается.
Для расчета работы силы упругости при переходе пружины (тела) из недеформированного состояния в деформированное используют формулу

Мощность
Скалярная величина, которая характеризует быстроту выполнения работы (можно провести аналогию с ускорением, которое характеризует быстроту изменения скорости). Определяется по формуле
Коэффициент полезного действия
КПД — это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время
Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии.
КПД наклонной плоскости — это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости.
Главное запомнить
1) Формулы и единицы измерения;
2) Работу выполняет сила;
3) Уметь определять угол между векторами силы и перемещения
Консервативные (потенциальные) и неконсервативные (непотенциальные) силы*
Формула нахождения работы*
Механическая работа. Мощность
Введение
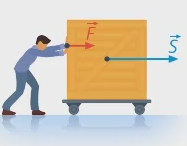
Тема урока – работа. Мы часто используем это понятие. Например, рабочий устал, потому что проделал большую работу: перенес 200 кирпичей с первого этажа на второй (см. рис. 1).
Рис. 1. Совершение работы
Мы знаем, почему он устал: он в это время прикладывал к кирпичам силу. Но только ли в силе дело? Наверняка, если бы он переносил кирпичи на третий этаж, он бы выполнил бόльшую работу, а если он бы толкал неподвижную стену, никакой работы выполнено бы не было, хотя рабочий бы устал. Значит, дело не только в силе, перемещение тоже играет роль. Сегодня мы четко определим понятие работы в физике.
Оно близко к бытовому понятию работы, но нужно понимать важный момент.
Понятие «работа»
В бытовом представлении работу выполняет человек, двигатель или другой субъект. В физике определение должно быть четким: субъект работы – сила. Поэтому работа, выполненная при действии нескольких сил, равна сумме работ, выполненных каждой силой по отдельности.
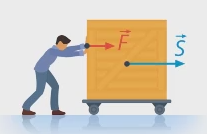
Как мы увидели на примере, работа тем больше, чем больше приложенная сила и чем больше пройденный путь. И сила, и перемещение – векторы, они имеют направления. Рассмотрим пока случай, когда направления векторов силы и перемещения совпадают (см. рис. 2), работа в физике определяется именно так:
т. е. как физическая величина, пропорциональная силе и перемещению.
Рис. 2. Направления векторов силы и перемещения совпадают
Соответственно, единицей работы является произведение единицы силы на единицу пути, т. е. 
Пример 1. Перемещение и сила совпадают
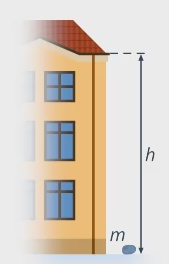
Рассмотрим такой пример: с крыши дома высотой 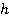
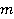
Рис. 3. Падение камня с крыши дома
Работа – это сила, умноженная на перемещение. Сила тяжести, действовавшая на камень, равна 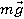
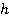
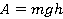
Рис. 4. Определение работы
Важно заметить, что нам безразлично, придавала ли данная сила ускорение телу. Рассмотрим ту же задачу, но с условием, что камень не падает, а осторожно, с постоянной скоростью опускается на веревке. Сила тяжести будет та же, как и перемещение, поэтому работа будет та же, 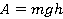
Рис. 5. Камень опускают с крыши дома
Нам важно лишь то, как сила участвует в движении, в какой степени она на него влияет. Но не всегда сила направлена туда же, куда и перемещение. Рассмотрим нашу задачу с новым условием: камень опускают по наклонной траектории под углом 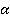
Рис. 6. Камень опускают по наклонной траектории
На перемещение 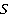
Рис. 7. Составляющая силы тяжести
Из прямоугольного треугольника проекция силы тяжести равна 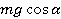
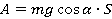
Рис. 8. Прямоугольный треугольник
Поскольку перемещение увеличилось, 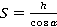
Мы получили формулу для работы в общем виде 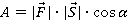
Формула 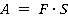
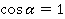
Рис. 9. Сила и перемещение сонаправлены
Пример 2. Сила и перемещение разнонаправлены
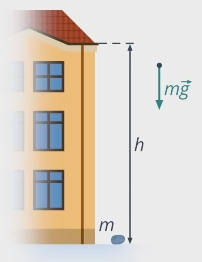
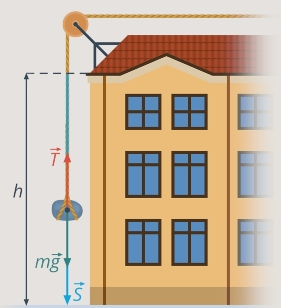
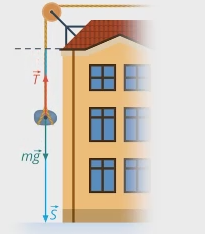
Вернемся к задаче о камне и рассмотрим другой частный случай, когда сила и перемещение направлены в противоположные стороны. Найдем теперь работу силы натяжения веревки, на которой камень спускают вертикально (см. рис. 10).
Рис. 10. Найдем силу натяжения веревки
Находим работу по той же формуле 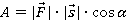
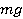
Почему
Откуда мы взяли, что 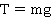
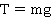
Рис. 11. Сила натяжения компенсирует силу тяжести
Угол между противоположно направленными векторами 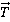
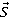
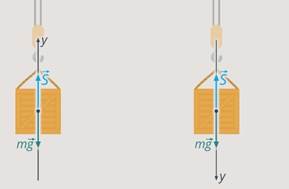
Результат согласуется с нашими представлениями: когда сила и перемещение направлены противоположно, мы получили отрицательную работу, и действительно, сила не способствует движению, а противодействует ему. Сила натяжения веревки «тащит» камень вверх, а он опускается вниз.
О выборе системы координат
Посмотрим, влияет ли на знак работы выбор системы координат. У нас есть тело, которое поднимается, т. е. движется вверх. Рассмотрим работу силы тяжести. Сила тяжести направлена вниз.
Попробуем направить ось координат вверх и вниз (см. рис. 12).
Рис. 12. Выбор направления оси y
В первом случае перемещение положительно, сила отрицательна. Работа будет равна:
Во втором случае перемещение отрицательно, сила положительна. Работа будет равна:
Таким образом, если сила выполняет отрицательную работу в данном направлении, то это происходит независимо от выбора системы координат, поэтому выбор делаем, как удобнее для решения задачи.
Об отрицательной работе
Отрицательные числа – это модель. В природе нет отрицательного количества. Есть количество, к примеру, 5 монет. -5 монет может значить, что эти же 5 монет забрали от начального количества. В физике мы часто сталкиваемся с векторными величинами: скорость, перемещение, сила и т. д. Их проекции на оси координат могут быть отрицательными. Если проекция скорости равна -5 м/с, это значит, что тело движется со скорость 5 м/с против направления оси координат (см. рис. 13).
Рис. 13. Направление скорости против оси координат
Знак показывает направление относительно выбранной оси координат.
Что значит отрицательная работа? Работа не вектор, у нее нет направления и ее нельзя рассматривать в проекции на оси координат. Что тогда значит минус? Работа – это произведение двух векторов, силы и перемещения, и знак работы тоже показывает направление одного вектора относительно другого, без привязки к оси координат.
Пример 3. Сила и перемещение перпендикулярны
Рассмотрим еще один случай: камень не опускали, а переместили горизонтально на расстояние 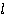
Рис. 14. Сила натяжения нити работу не совершает
Тогда работа силы натяжения нити равна 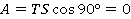
Рис. 15. Сила, которая совершает работу
Здесь результат тоже логичен: проекция силы натяжения на горизонтальное направление равна нулю, поэтому эта сила не влияет на движение тела в данном направлении и, соответственно, не совершает работы по перемещению в данном направлении.
Противоречие жизненному опыту
Кажется, что это не согласуется с нашим жизненным опытом. Если груз тяжелый и нести его далеко, то человек устает, а мы утверждаем, что работы по перемещению груза он не совершает. Дело в том, что чувство усталости не всегда определяется работой как физической величиной, человек устает от длительного напряжения мышц, расхода химической энергии, накопления продуктов обмена.
То же самое мы наблюдаем в случае с человеком, толкающим неподвижную стену или держащим кирпич на вытянутой руке (см. рис. 16).
Рис. 16. Работа не совершается
Человек устанет, в случае с кирпичом даже очень быстро, но работа будет совершена нулевая: и стена, и кирпич неподвижны, перемещение равно нулю.
Как видим, во всех случаях справедливо одно общее выражение: 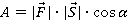
Задача 1
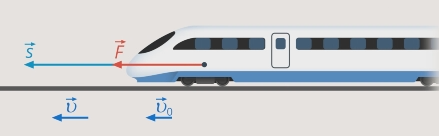
Какую работу надо совершить, чтобы заставить поезд массой 800 т: а) увеличить свою скорость от 36 до 54 
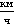
Задача на работу. Работу будет совершать сила тяги поезда 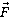
Рис. 17. Сила тяги совершает работу
Пользуемся определением работы, это скалярное произведение суммы и перемещения:
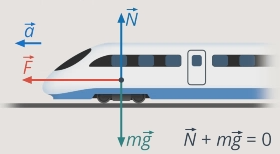
Тело движется с ускорением под действием силы тяги, применим второй закон Ньютона (сразу учтем, что сила тяжести и сила реакции опоры компенсируются) (см. рис. 18).
Рис. 18. Применяем второй закон Ньютона
Тело движется с ускорением, изменяет скорость с 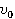
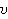
Путь при равноускоренном движении равен:
Выберем систему координат. Удобно направить ось х в направлении движения поезда (см. рис. 19).
Рис. 19. Выбор направления оси х
Тогда проекции скоростей и перемещения будут положительны, проекция ускорения определяется разностью 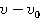
Получим систему уравнений, которую остается только решить, а это задача математическая:
Решив систему уравнений, получаем ответ:
Вычислим для двух случаев, заданных в условии. Поезд разгоняется от 36 км/ч до 54 км/ч. В СИ значения скорости будут равны 10 м/с и 15 м/с. Масса равна 800 т или 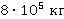
Поезд тормозит от 72 км/ч до 0 км/ч. В СИ начальная скорость равна 20 м/с.
Ответ: 50 (МДж); -160 (МДж).
В первом случае скорость увеличивалась, значит, ускорение и сила были сонаправлены со скоростью и перемещением (см. рис. 20).
Рис. 20. Ускорение и сила сонаправлены со скоростью и перемещением
Сила сонаправлена с перемещением, работа в этом случае положительна, что мы и получили. Во втором случае скорость уменьшалась, значит, ускорение и сила направлены противоположно скорости и перемещению. Сила направлена противоположно перемещению, работа отрицательна (см. рис. 21).
Рис. 21. Сила направлена противоположно перемещению
Мы все сделали правильно.
На следующем уроке разберем это более подробно, но можем заметить, что 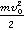
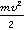
Рассмотрим еще несколько примеров того, как силы выполняют работу.
Нет специфических правил для каждой силы, они все подчиняются одному выражению 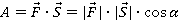
Рис. 22. Работа силы тяги
Чаще всего (но не всегда) работа силы трения отрицательна, т. к. она направлена против направления движения скользящего тела (см. рис. 23).
Рис. 23 . Работа силы трения
Чаще всего (но не всегда) тела движутся вдоль поверхности, в то время как сила реакции опоры направлена перпендикулярно ей, поэтому работа силы реакции опоры равна нулю. Но это лишь тенденции, которые говорят, как бывает чаще всего, мы же подчиняем все случаи одному закону 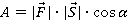
Задача 2
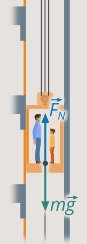
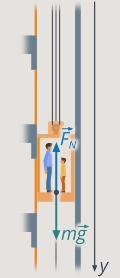
Лифт начинает движение вниз и через 3 с достигает скорости 1,5 м/с. Найти работу силы реакции опоры по перемещению груза за это время, если масса груза в лифте равна 140 кг.
В задаче описан груз, который движется под действием силы тяжести и силы реакции опоры. Рассмотрим силу реакции опоры. Работа находится как скалярное произведение 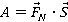
Рис. 24. Нахождение работы
Тело движется с ускорением под действием разных сил, этот процесс подчиняется второму закону Ньютона и описывается формулами кинематики.
Сразу учтем, что 
Путь при равноускоренном движении равен:
Направим ось координат у вдоль движения лифта, вертикально вниз (см. рис. 25).
Рис. 25. Выбор направления оси y
Тогда в проекции на ось у получим:
Вычислим:
Ответ: -3 (кДж).
Задача решена.
Мощность
Когда мы оцениваем качество работника (или механизма, или двигателя), нам мало руководствоваться только тем, какую работу он выполнил. Нас еще интересует, как быстро он ее выполняет. Можно совершить работу за час и быть молодцом, а можно потратить на ту же работу целый день: работа выполнена, результат тот же, но медленно. Для характеристики быстроты или скорости выполнения работы вводится величина мощность. Мы уже сталкивались с величинами, характеризующими быстроту (скоростью, ускорением), поэтому знаем, что быстрота изменения какой-либо величины – это изменение величины, деленное на промежуток времени, на протяжении которого величина изменялась.
Так же и мощность – это работа, деленная на время ее выполнения:
Единица мощности называется ватт (Вт).
Почему иногда совершается небольшая работа при большой мощности
Не всегда большая мощность означает, что выполняется большая работа. Например, мощность разряда молнии огромна, она может достигать 200 ГВт, не каждая электростанция развивает такую мощность. Совершённая при этом работа может пойти на нагревание и ионизацию воздуха, на вспышку света, на выведения из строя электросети, если ударит в линию электропередач, и т. д. Вычислим ее, если длительность разряда молнии равна около 0,001 с, и получим около 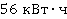
Это как с механической скоростью движения: рекорд скорости футбольного мяча –200 км/ч. Вертолет на такой скорости за двое суток пересечет всю Россию с запада на восток. Скорость большая, но мяч на такой скорости движется доли секунды и успевает лишь долететь до ворот на несколько десятков метров.
Задача 3
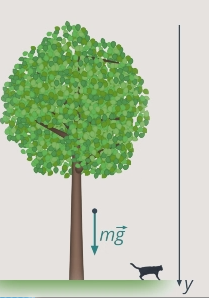
Какую среднюю мощность развивает сила тяжести в процессе падения кота массой 2 кг с дерева высотой 3 м?
Задача на мощность, используем определение мощности как скорости совершения работы:
Работа – это сила, умноженная на перемещение:
(в нашем случае сила тяжести 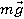
Для задач на движение мы можем также применять законы кинематики. За время падения кот, двигаясь равноускоренно из состояния покоя, пройдет путь:
Направим ось у вертикально вниз вдоль перемещения кота (см. рис. 26).
Рис. 26. Выбор направления оси y
Тогда в проекции на ось у запишем систему уравнений, которую остается только решить:
Ответ: 77,5 (Вт).
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
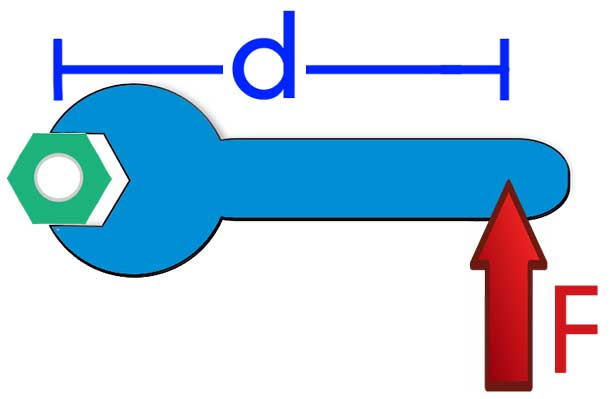
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Обновлено: 28.05.2023
Друзья, сегодня разберем с вами задачку на стыке механики и кинематики. Потренируемся в нахождение работ различных сил, посмотрим на связь этих работ с потенциальной и кинетической энергиями. Рассмотрим это на примере следующей задачи.
Задача
Тело массой 3 кг под действием силы F перемещается вниз по наклонной плоскости на расстояние L = 5 м, расстояние тела от поверхности Земли при этом уменьшается на h = 3 м. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 20 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F ? (Ответ дайте в джоулях.) Ускорение свободного падения примите равным 10 м/с², коэффициент трения μ = 0.5.
Статика — один из разделов современной физики, который изучает условия нахождения тел и систем в механическом равновесии. Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.
Второй и третий законы Ньютона
Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.
Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:
Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.
Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:
Эта запись является математическим выражением для третьего ньютоновского закона.
При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.
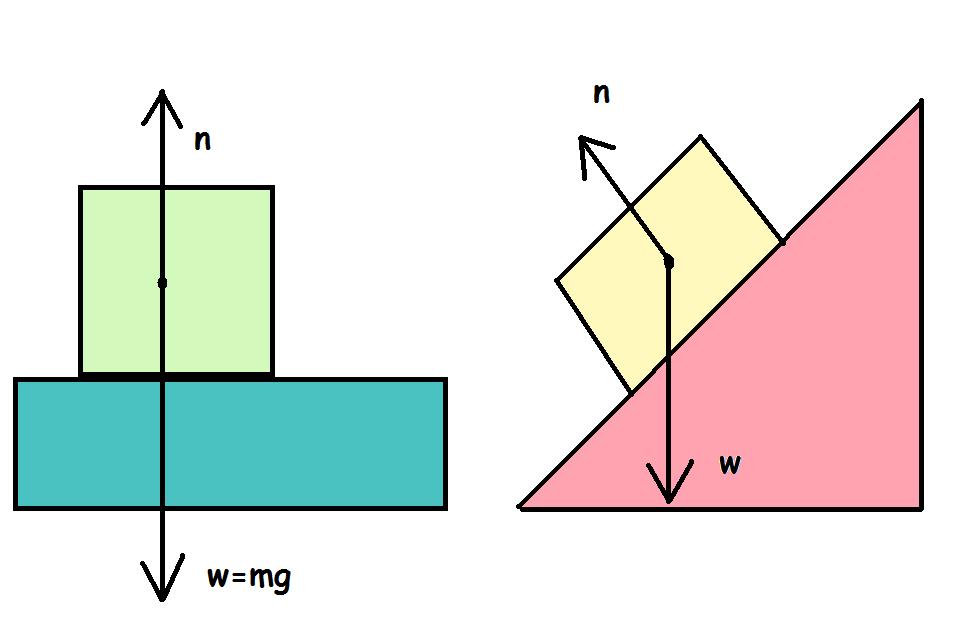
Сила реакции опоры
Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.
Сила N — это контактная величина. Если имеется контакт между телами, то она появляется всегда. В примере выше значение величины N равно по модулю весу тела. Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела — это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.
Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.
Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).
Физическая причина появления силы N
Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.
Если рассматривать вопрос на атомном уровне, то появление величины N — это результат действия принципа Паули. При небольшом сближении атомов их электронные оболочки начинают перекрываться, что приводит к появлению силы отталкивания.
Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.
Как вычислять силу N?
Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.
Методика определения величины N заключается в следующем:
- сначала записывают второй закон Ньютона для данной системы, учитывая все действующие в ней силы;
- находят результирующую проекцию всех сил на направление действия реакции опоры;
- решение полученного уравнения Ньютона на отмеченное направление приведет к искомому значению N.
При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.
Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.
Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.
Задача со стаканом на столе
Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?
Запишем динамическое уравнение. Имеем:
Здесь P1 и P2 — вес стакана с водой и книги соответственно. Поскольку система находится в равновесии, то a=0. Учитывая, что вес тела равен силе тяжести, а также пренебрегая массой пластикового стакана, получаем:
Учитывая, что плотность воды равна 1 г/см 3 , и 1 мл равен 1 см 3 , получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.
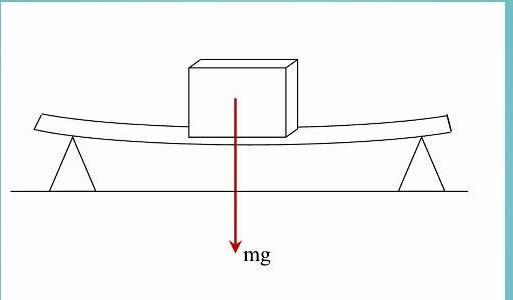
Задача с доской, двумя опорами и грузом
Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?
Прежде чем переходить к решению задачи, следует ввести понятие момента силы. В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.
Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:
Здесь L/2 — рычаг действия силы тяжести. Знак минус появился потому, что момент M1 осуществляет вращение против часовой стрелки.
Момент силы реакции опоры будет равен:
Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:
Заметим, что от длины доски сила N не зависит.
Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.
Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.
Тело находится на выпуклой или вогнутой поверхности
Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой (vec). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.
Примечания:
- Нормаль – значит, перпендикуляр.
- Искривленную, т.е., выпуклую, или вогнутую поверхность, можно считать частью сферы. Центр сферы – точка, она находится внутри сферы, от этой точки к поверхности сферы можно провести радиус.
(vec left( H right) ) – сила, с которой опора действует на тело.
Рис. 1. Тело (шар) опирается на выпуклую – а) и вогнутую – б) поверхность. А поверхность реагирует на вес тела силой нормальной реакции
Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.
Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция (vec) направлена по радиусу внутрь сферической поверхности к ее центру.
Тело опирается на поверхность в двух точках
На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.
Рис. 2. Однородный стержень опирается на поверхность двумя точками, в каждой из точек сила реакции располагается перпендикулярно поверхности
В точках соприкосновения поверхность отвечает телу силой (vec) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.
Cилы реакции (vec>) и (vec>) имеют различные направления и в общем случае не равны по модулю.
Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.
Как рассчитать силу нормальной реакции
Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.
Примечание: Сила реакции (vec) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.
Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.
На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.
Рис. 3. Тело опирается на поверхность горизонтальную – а) и наклонную – б), составляя силовые уравнения для сил, расположенных перпендикулярно соприкасающимся поверхностям, рассчитывают силу реакции опоры
Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.
По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.
(m vec left( H right) ) – сила, с которой тело действует на опору;
(vec left( H right) ) – сила, с которой опора отвечает телу;
Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы (m vec) на ось — это (mg_), она будет направлена противоположно реакции опоры (vec) и численно равна ей.
Если тело лежит на внутренней поверхности сферы, сила vec направлена к центру сферы.
Если тело лежит на внешней поверхности сферы, сила vec направлена от центра сферы.
3. Сила натяжения нити
Сила, действующая со стороны нити (веревки, каната, троса, стержня и т.п.) на тело, которое висит на нити (веревке и т.п.). Направлена вдоль нити (и т.п.).
vec –Сила натяжения нити.
4. Вес тела
Определение: – это сила, с которой тело давит на опору или растягивает подвес.
Вес тела равен по модулю силе реакции опоры или силе натяжения нити, направлен в противоположную сторону и приложен к другому телу: либо опоре, либо нити.
vec –сила реакции опоры;
5. Сила трения
a) Сила трения скольжения
Сила трения скольжения направлена противоположно относительной скорости тел и не зависит от площади соприкосновения поверхностей.
vec_ –сила трения скольжения.
Модуль силы трения равен произведению коэффициента трения скольжения на модуль силы реакции опоры:
mu –коэффициент трения скольжения.
b) Сила трения качения
Действует на тело, которое не скользит, а катится по некоторой поверхности.
vec_ –сила трения качения.
mu _ –коэффициент трения качения.
Коэффициент трения качения много меньше коэффициента трения скольжения
c) Сила трения покоя
Действует на тело, лежащее неподвижно на некоторой поверхности, которое мы пытаемся сдвинуть с места. Противоположно направлена внешней силе и равна ей по модулю.
vec_ – сила трения покоя.
vec_ – внешняя сила.
6. Схема решения задач
a) Нарисовать все силы, приложенные ко всем телам системы;
b) Выбрать системы отсчета (можно свою для каждого тела);
c) Спроектировать силы на оси;
d) Записать уравнения для второго закона Ньютона в проекциях для всех тел системы;
e) Записать кинематические связи, то есть связи между скоростями и ускорениями различных тел системы;
Решение. Рассмотрим сначала случай k > tg α . В этом случае тело, помещенное на наклонную плоскость, будет покоится (см. пример 6.4), и чтобы спустить его по плоскости на него нужно действовать силой, направленной вниз вдоль плоскости (см. рис. 10.1). Поскольку по условию тело спускают медленно, его ускорение равно нулю и, следовательно
(здесь использовано то обстоятельство, что действующая на тело при его движении по наклонной плоскости сила трения равна kmg cos α , проекция силы тяжести на направление плоскости — mg sin α ). Так как в процессе движения тела по наклонной плоскости действующие на него силы не меняются, для нахождения их работ воспользуемся формулой (10.3).
Работа силы тяжести. Угол между силой тяжести и перемещением вдоль плоскости равен 90° − α , перемещение h / sin α . Поэтому
Работа силы трения. Угол между силой трения и перемещением вдоль плоскости равен 180°, перемещение h / sin α . Поэтому
Работа силы реакции опоры. Угол между этой силой и перемещением тела равен 90°, его косинус равен нулю, поэтому
Работа внешней силы F . Используя формулу (10.4), получим
Работа равнодействующей силы. Поскольку тело спускают медленно, его ускорение равно нулю, следовательно, равна нулю равнодействующая всех сил, действующих на тело, и, следовательно, равна нулю ее работа:
Читайте также:
- Какими способами ученики овладевают знаниями в древнем шумере и в современной школе
- План открытого урока по русскому языку в 5 классе
- Почему реформы братьев гракхов потерпели поражение кратко
- Компетентность педагога доу в условиях реализации национального проекта образование
- Parts of the body план урока
Работа силы тяжести. Работа реакции опоры. Работа силы трения. Работа силы натяжения веревки. Работа равнодействующей силы
Лекция №3 по динамике
Работа
Работа — это скалярная величина, которая определяется по формуле
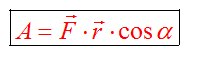
Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение.
Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.
Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.
Угол между вектором силы и перемещением
1) Верно определяем направление силы, которая выполняет работу;
2) Изображаем вектор перемещения;
3) Переносим вектора в одну точку, получаем искомый угол.
На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r.
Работа силы тяжести
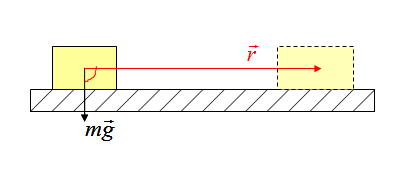
Работа реакции опоры
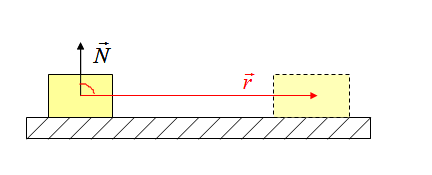
Работа силы трения
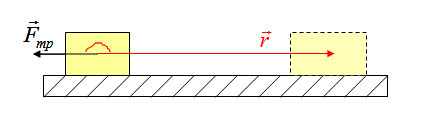
Работа силы натяжения веревки
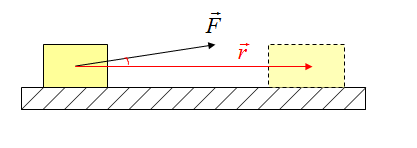
Работа равнодействующей силы
Работу равнодействующей силы можно найти двумя способами:
1 способ — как сумму работ (с учетом знаков «+» или «-«) всех действующих на тело сил, в нашем примере.
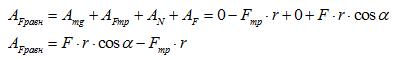
2 способ — в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок