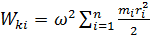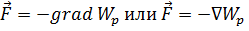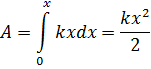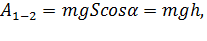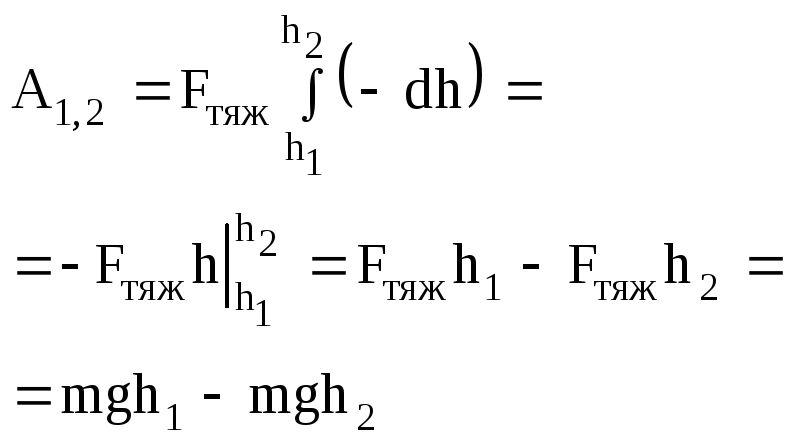Как найти работу силы тяжести при движении

Совсем недавно, мы
изучили работу силы. Напомним, что работа силы равна произведению модуля силы,
модуля перемещения и косинуса угла между направлениями силы и перемещения:

Рассмотрим теперь частный
случай — работу силы тяжести при перемещении тела с высоты h₁
на высоту h₂.

Первый случай — это
падение тела вертикально вниз.

В этом случае,
перемещение, конечно же, будет равно

Сила тяжести, как мы
знаем, равна

.

Поскольку сила тяжести
направлена вертикально вниз, как и перемещение, косинус угла между
направлениями этих векторов равен единице. Таким образом, мы получим, что
работа силы тяжести равна:

Второй случай — это когда
тело, наоборот, подбрасывают вертикально вверх с высоты h₁
на высоту h₂.

В этом случае, угол между
направлением силы тяжести и направлением перемещения составит 180^о.
Это приводит нас к тому, что работа силы тяжести опять-таки равна:

Наконец, рассмотрим
случай, когда между направлением силы тяжести и перемещением существует
произвольный угол α.

Обозначим модуль
перемещения за s. В этом случае,
работа силы тяжести равна:

Но, исходя из определения
косинуса:

Таким образом, мы в
третий раз получили одинаковый результат.

Более того, если даже мы
рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.

Любую кривую мы можем
представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и
вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет
равна нулю, поскольку в этом случае направление перемещения перпендикулярно
направлению силы тяжести. На вертикальных участках работа будет равна: A
= mg(s₁
+ … + s_n).
Очевидно, что эта сумма будет равна (h₁
– h₂):

Таким образом, мы
убедились, что работа силы тяжести не зависит от траектории движения тела.
Имеет значение лишь то, насколько начальное положение тела отличается от
конечного. Это плавно подводит нас к понятию потенциальной энергии, которое
мы рассмотрим немного позже.

Из приведенных примеров
вытекает еще один важный вывод: при движении тела по замкнутой траектории
работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму
прямоугольника. Как мы уже убедились, при движении тела в горизонтальном
направлении, работа силы тяжести равна нулю. Вектор перемещения направлен
перпендикулярно вектору силы тяжести. При перемещении же по противолежащим
вертикальным сторонам контура, сила тяжести совершает работу, равную по
абсолютной величине, но противоположную по знаку.

В одном случае вектор
перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в
противоположную сторону. Это довольно логично, поскольку при движении тела
вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.

Мы можем сколь угодно
усложнить эту траекторию, получив совершенно произвольный замкнутый контур.

Но опять же, разбив все
кривые на ломаные линии с горизонтальными и вертикальными участками, мы
убедимся, что суммарная работа будет равна нулю.

Силы, обладающие такими
свойствами, называются консервативными. То есть, консервативная сила — это
такая сила, работа которой в замкнутом контуре равна нулю.

Примеры решения задач.

Задача 1. Охотник
стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы
тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы,
то какова её масса?

Задача 2. Находясь
на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом
перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна
5 кг, то каково ускорение свободного падения на Нептуне?

Полезно ознакомиться в отдельности с работой каждой из механических сил, с которыми мы ознакомились в пятой главе: силы тяжести, силы упругости и силы трения. Начнем с силы тяжести. Сила тяжести равна $vec{F} = m vec{g}$ и направлена по вертикали вниз. Вблизи поверхности Земли ее можно считать постоянной.

рис. 1

При движении тела по вертикали вниз сила тяжести совпадает по направлению с перемещением. При переходе с высоты $h_{1}$ над каким-то уровнем, от которого мы начинаем отсчет высоты, до высоты $h_{2}$ над тем же уровнем (рис. 1), тело совершает перемещение, по абсолютной величине равное $h_{1} — h_{2}$. Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:

$A = mg (h_{1} — h_{2})$.

Высоты $h_{1}$ и $h_{2}$ не обязательно отсчитывать от поверхности Земли. Для начала отсчета высот можно выбрать любой уровень. Это может быть пол комнаты, стол или стул, это может быть и дно ямы, вырытой в земле, и т. д. Ведь в формулу для работы входит разность высот, а она не зависит от того, откуда начинать их отсчет. Мы могли бы, например, условиться начинать отсчет высоты с уровня $B$ (см. рис. 1). Тогда высота этого уровня была бы равна нулю, а работа выражалась бы равенством

$A = mgh$,

где $h$ — высота точки $A$ над уровнем $B$.

Если тело движется вертикально вверх, то сила тяжести направлена против движения тела и ее работа отрицательна. При подъеме тела на высоту $h$ над тем уровнем, с которого оно брошено, сила тяжести совершает работу, равную

$A = — mgh$.

Если после подъема вверх тело возвращается в исходную течку, то работа на таком пути, начинающемся и кончающемся в одной и той же точке (на замкнутом пути), на пути «туда и обратно», равна нулю. Это одна из особенностей силы тяжести: работа силы тяжести на замкнутом пути равна нулю.

Теперь выясним, какую работу совершает сила тяжести в случае, когда тело движется не по вертикали.

рис. 2

В качестве примера рассмотрим движение тела по наклонной плоскости (рис. 2). Допустим, что тело массой $m$ по наклонной плоскости высотой $h$ совершает перемещение $vec{s}$, по абсолютной величине равное длине наклонной плоскости. Работу силы тяжести $m vec{g}$ в этом случае надо вычислять по формуле $A = mgs cos alpha$. Но из рисунка видно, что

$cos alpha = frac{h}{s}$.

Поэтому

$A = mgs frac{h}{s} = mgh$.

Мы получили для работы то же самое значение.

рис. 3

Выходит, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. При одной и той же «потере высоты» работа силы тяжести одинакова (рис. 3).

рис. 4

Это справедливо не только при движении по наклонной плоскости, но и по любому другому пути. В самом деле, допустим, что тело движется по какому-то произвольному пути, например по такому, какой изображен на рисунке 4. Весь этот путь мы можем мысленно разбить на ряд малых участков: $AA_{1}, A_{1}A_{2}, A_{2}A_{3}$ и т. д. Каждый из них может считаться маленькой наклонной плоскостью, а все движение тела на пути $AB$ можно представить как движение по множеству наклонных плоскостей, переходящих одна в другую. Работа силы тяжести на каждой такой наклонной плоскости равна произведению $mg$ на изменение высоты тела на ней. Если изменения высот на отдельных участках равны $h_{1}, h_{2}, h_{3}$ и т. д., то работы силы тяжести на них равны $mgh_{1}, mgh_{2}, mgh_{3}$ и т. д. Тогда полную работу на всем пути можно найти, сложив все эти работы:

$A = mgh_{1} + mgh_{2} + mgh_{3} + cdots = mg (h_{1} + h_{2} + h_{3} + cdots)$.

Но

$h_{1} + h_{2} + h_{3} + cdots = h$.

Следовательно,

$A = mgh$.

Таким образом, работа силы тяжести не зависит от траектории движения тела и всегда равна произведению силы тяжести на разность высот в исходном и конечном положениях. При движении вниз работа положительна, при движении вверх — отрицательна.

Почему же в технике и быту при подъеме грузов часто пользуются наклонной плоскостью? Ведь работа перемещения груза по наклонной плоскости такая же, как и при движении по вертикали!

Это объясняется тем, что при равномерном движении груза по наклонной плоскости сила, которая должна быть приложена к грузу в направлении перемещения, меньше силы тяжести. Правда, груз при этом проходит больший путь. Больший путь — это плата »а то, что по наклонной плоскости груз можно поднимать с помощью меньшей силы.

Подробности

Обновлено 30.05.2018 20:11

Просмотров: 707

Задачи по физике — это просто!

Вспомним

Формулы, по которым можно вычислить работу силы:

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Задача 2

Какую работу совершит сила тяжести при падении мяча массой 0,5 кг на землю из состояния покоя с высоты 5 метров?

Задача 4

Скорость падающего кирпича массой 2 кг на некотором отрезке пути изменилась от 3 м/с до 6 м/с. Определить работу, совершенную силой тяжести.

Работа силы тяжести. Потенциальная энергия тела, поднятого над землей

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим различное движение тела под действием силы тяжести и научимся находить работу этой силы. Также введём понятие потенциальной энергии тела, узнаем, как связана эта энергия с работой силы тяжести, выведем формулу, по которой находится эта энергия. С помощью данной формулы решим задачу, взятую из сборника для подготовки к единому государственному экзамену.

Работа силы тяжести.

Рассмотрим тело, скользящее по наклонной плоскости с углом наклона α и высотой Н. Выразим Δх через H и α:

.

Учитывая, что сила тяжести F_т = mg составляет угол (90° — α) с направлением перемещения, используя формулу , получим выражение для работы силы тяжести A_g:

.

Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла на­клона плоскости.

Отсюда следует, что:

1. работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;

2. при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).

Работа сил реакции, как следует из рисунка, равна нулю, поскольку сила реакции (N) на­правлена перпендикулярно перемещению Δх.

II. Работа силы при вращательном движении

Элементарная работа силы, действующей на i-тую материальную точку тела, вращающегося относительно неподвижной оси, может быть представлена в виде:

Учтем, что за малый промежуток времени dt путь, пройденный материальной точкой dl, представляет собой длину дуги окружности, по которой движется точка: dl = R·dφ.

Следовательно, dA = F·cosα·dl = F·cosα·R·dφ

С другой стороны, из определения момента силы при движении тела вокруг закрепленной оси: M = R·F.

Таким образом, с учетом скалярного произведения векторов получим:

dA = M·cosα·dφ = (M·dφ)

Полная работа при вращательном движении равна:

A = ∫dA = ∫M·cosα·dφ = ∫(M·dφ)

III. Энергия механического движения.

К механической энергии относят два вида энергии – кинетическую (W_k) и потенциальную (W_p). Чтобы получить выражение энергии в виде функции параметров состояния механического движения, надо найти, как изменяется величина энергии с изменением величины параметров.

Кинетической энергией называется энергия движущегося тела.

Для вычисления кинетической энергии подсчитаем работу, которую должна произвести результирующая сила F, чтобы тело массы m изменило скорость своего движения от V₁ до V₂ .

(4)

– кинетическая энергия тела. Из этой формулы следует, что кинетическая энергия тела не может быть отрицательной. Так как скорость относительная величина, то и кинетическая энергия тоже является относительной величиной.

Любую механическую систему можно представить как систему материальных точек, то кинетическая энергия механической системы может быть найдена как сумма кинетических энергий всех материальных точек, образующих эту систему: . Таким образом, кинетическая энергия механической системы является функцией состояния ее движения.

Работа равнодействующей силы равна изменению кинетической энергии тела, при изменении скорости его движения от V₁ до V₂: А = DЕ_К

Если действует ещё сила трения, то A_тр 2

равна:

Просуммировав по всем элементам, получим:

– момент инерции тела, относительно оси вращения.

(11)

Если твердое тело одновременно участвует в двух движениях: поступательном со скоростью и вращательном со скоростью , то

(12)

Полная кинетическая энергия твердого тела равна сумме кинетической энергии W_п поступательного движения центра масс тела и кинетической энергии вращения W_в.

Если на систему материальных точек или тел действуют консервативные силы, то можно ввести понятие потенциальной энергии этой системы.

Потенциальная энергия — энергия, обусловленная взаимным расположением тел или частей одного и того же тела и характером их взаимодействия.

Потенциальная энергия системы тел (или тела) может быть определена, если указаны взаимное расположение тел в системе и силы, действующие между ними.

рис. 1.9

В процессе перемещения материальной точки на dr внешняя сила F совершит работу dA = F·dr. При этом перемещении скорость тела не изменилась (была V = 0 и стала V = 0), значит в результате совершённой работы, произошло изменение другой (не кинетической) формы энергии, зависящей от координат положения тела, т.е. нужно говорить о потенциальной энергии.

Обозначим через dW_p – изменение потенциальной энергии при перемещении точки в силовом поле. Согласно определению работы, можно записать:

(5)

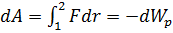
Работа, совершаемая силами F, действующими на материальную точку при её перемещении, равна изменению её потенциальной энергии.

Равенство (5) надо понимать алгебраически:

а) если dA > 0, то потенциальная энергия уменьшается (dW_p 0).

Учитывая, что 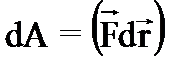, имеем:

(6)

Это соотношение между силой и потенциальной энергией является одним из основных соотношений механики.

Выражение называется градиентом изменения потенциальной энергии на пути S.

Где — оператор Набла, который приобретает смысл в сочетании со скалярной или векторной величиной, на которую он символически умножается. Если оператор Набла символически умножить на скаляр, то получим вектор, который называется градиентом функции.

Из этого выражения (6) следует:

а) Сила направлена всегдав сторону уменьшения потенциальной энергии.

б) производная обращается в ноль в точках, где функция достигает максимума или минимума, а это значит – где потенциальная энергия имеет максимум или минимум, там сила равна нулю.

Уравнение (5) не даёт полного определения величины потенциальной энергии в каждой точке, а определяет лишь изменение потенциальной энергии при переходе от точки к точке. Абсолютная величина W_p зависит от выбора начала отсчёта потенциальной энергии (где потенциальная энергия равна нулю). Обычно, за начало отсчёта выбирают такое положение, при котором взаимодействие практически отсутствует (когда тела удалены в бесконечность).

Вычислим величину потенциальной энергии в двух случаях:

1. Потенциальная энергия тяготения.

Откуда получим:

В частном случае, при r₁ = 0, (на поверхности Земли), r₂ = H, (над поверхностью Земли)

2.Потенциальная энергия упругодеформированного тела.

Покажем, что работа силы тяжести одинакова для двух разных путей (для пути 1 — 3 и пути 1 — 2 — 3), обозначения длин путей приведены на рис. 1.10.

Из последней формулы следует, что работа силы тяжести не зависит от формы траектории. А вдоль замкнутой траектории равна нулю, что подтверждает вывод о консервативной природе силы тяжести.

Полной механической энергией системы называют величину, равную сумме кинетической и потенциальной энергии этой системы:

Полная механическая энергия также является функцией состояния, как и каждое из слагаемых.

у

Найдем работу, которую совершает сила
тяжести
,
действующая на падающее тело массойm,
при его перемещении из точки 1 в точку
2 по произвольному пути (рис.4.6).

Полная работа:

.

Силу тяжести при
можно считать постоянной, тогда

.

Так как
направление вектора
противоположно возрастанию высотыh(α = 180), то

.

Работа силы тяжести равна убыли
потенциальной энергии, зависит от
начального и конечного положений тела
над Землей и не зависит от формы траектории
его движения. Следовательно, сила тяжести
есть консервативная сила.

3.6.3. Потенциальная энергия пружины

Внешняя сила, сжимая или растягивая
пружину, совершает работу. Освобожденная
от внешнего воздействия, пружина
восстанавливает свою форму, а потенциальная
энергия, запасенная пружиной в процессе
деформации, превращается в другие виды
энергии. Мерой энергии превратившейся
в другие виды, является величина работы,
совершенная упругой силой.

Работа упругой силы
на участкеdx

dA = F_хdx = – kxdx,

Полная
работа при изменении длины пружины на
Δх = х₂ – х₁

(3.25)

Потенциальная энергия деформированной
пружины

(3.26)

где
С = 0, так как потенциальная энергия
недеформированной пружины равна нулю.

Работа
упругой силы не зависит от того, как
произошло изменение длины пружины.
Поэтому упругая сила так же как и сила
гравитационного притяжения консервативна.

3.6.4. Потенциальный барьер и яма

Потенциальная энергия может быть
представлена графически. График,
выражающий зависимость потенциальной
энергии от соответствующей координаты,
называется потенциальной кривой. По
характеру потенциальной кривой
определяется величина и направление
силы, действующей на тело вдоль
соответствующего направления.

Проанализируем одну из возможных
потенциальных кривых. Возьмем кривую
изменения потенциальной энергии Е_псистемы тел, когда в системе одно тело
перемещается вдоль оси х (рис. 3.12). Сила
действующая на тело

.

где
– угол наклона к оси касательной
проведенной в соответствующей точке
кривой Е_п=f(x)
.

B точке х₁(,
поэтому)cила противоположна
направлению х и препятствует удалению
тела из системы. В точке х₂(tgα < 0,
силаF_х > 0)
силаF_хсовпадает
с направлением оси х, и способствует
движению тела в данном направлении. В
точке х₀(tgα = 0) сила на
тело не действует. Величину силы можно
определить по крутизне потенциальной
кривой: чем круче кривая, тем больше
численное значениеtgα,
например, величина силы в точке 2 больше,
чем в точке 1.

Резкое возрастание потенциальной кривой
вдоль направления движения тела
определяет потенциальный барьер, который
характеризуется высотой и шириной. Так,
для тела, находящейся в точке с координатой
х₁, высота потенциального барьера
ΔЕ_п, ширина Δх = (х₂– x₁).

Если потенциальный барьер встречается
на пути движения тела, как в положительном,
так и в отрицательном направлении оси,
то, оно находится в потенциальной яме.
Форма и глубина потенциальной ямы
зависят от природы сил взаимодействия
и конфигурации системы тел.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #

  17.05.20158.11 Mб14курс лекций новый.doc

• #
• #
• #
• #