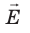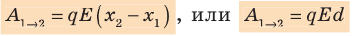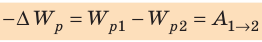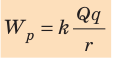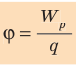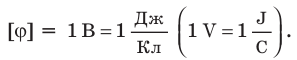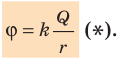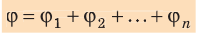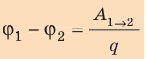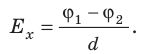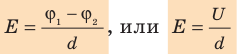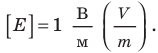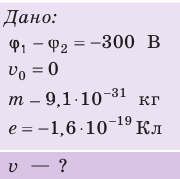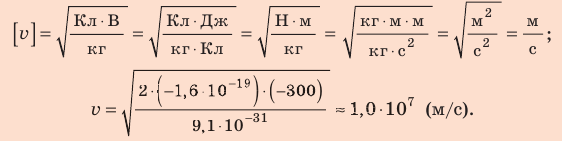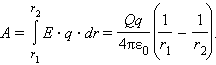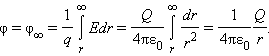Как найти работу совершаемую электрическим полем - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью

Вычислим работу А, которую совершает сила 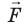, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

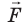
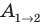
Поле однородное, поэтому сила постоянна, ее модуль равен: F=qE, а scosα=d=является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( ) равна:

Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 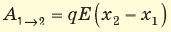будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.

Что называют потенциалом электростатического поля

Потенциал 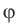электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

Единица потенциала в Си — вольт:

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 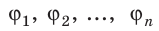полей, созданных каждым зарядом:

Как определяют разность потенциалов

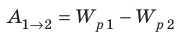
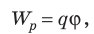
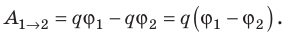
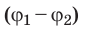
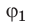
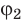
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: . Поскольку то Выражение называют разностью потенциалов, где — значение потенциала в начальной точке траектории движения заряда, — значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

Единица разности потенциалов в Си — вольт: 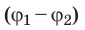= 1 В (V).

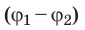
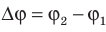
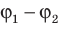
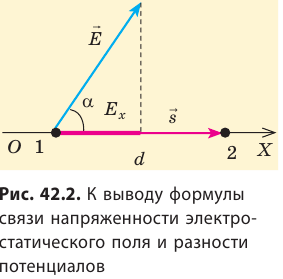
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов − также называют напряжением (U). Важно не путать изменение потенциала и разность потенциалов (напряжение) .

Как связаны напряженность однородного электростатического поля и разность потенциалов

Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

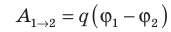
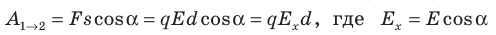
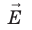
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2:; 2) через напряженность поля: — проекция вектора на ось Ох, проведенную через точки 1 и 2.

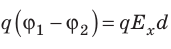
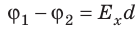
Приравняв оба выражения для работы, получим: , откуда: , или

Если заряд перемещается в направлении напряженности электрического поля () , последняя формула примет вид:

Из последней формулы следует единица напряженности в Си — вольт на метр:

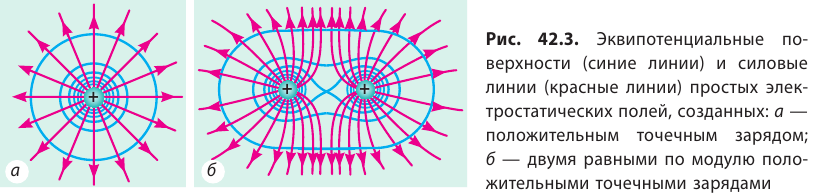
Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( ), а на эквипотенциальной поверхности .

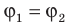
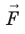
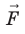
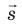
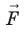
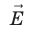
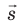
Работу электростатического поля также можно представить через силу , действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами и . Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы , а следовательно, и вектор напряженности поля в любой точке перпендикулярны вектору перемещения .

Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

Заказать решение задач по физике

Пример решения задачи

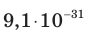
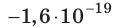
Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона кг, заряд Кл.

Заряд электрона — отрицательный, его начальная скорость 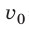= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.

Решение:

Поиск математической модели, решение Согласно теореме о кинетической энергии:

— работа сил поля.

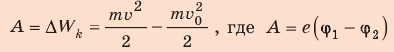
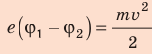
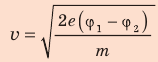
Таким образом, , отсюда .

Проверим единицу, найдем значение искомой величины:

Ответ:

Выводы:

Закон Ома для однородного участка электрической цепи
Закон Ома для полной цепи
Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
Сила и закон Ампера
Волновое движение в физике
Продольные и поперечные волны в физике
Звуковые волны в физике
Электрическое поле в физике

Источник

Работа электростатического поля

На электрические заряды в электростатическом поле действуют силы. Поэтому, если заряды перемещаются, то эти силы совершают работу. Рассчитаем работу сил однородного электростатического поля при перемещении положительного заряда q

из точки
A
в точку
B
(рис. 1).
Рис. 1
На заряд q

, помещенный в однородное электрическое поле с напряженностью
E
, действует сила (~vec F = q cdot vec E ). Работу поля можно рассчитать по формуле
(~A_{AB} = F cdot Delta r cdot cos alpha,)
где Δr

⋅cos α =
AC
=
x2
–
x1
= Δ
x
— проекция перемещения на силовую линию (рис. 2).
Рис. 2
Тогда

(~A_{AB} = q cdot E cdot Delta x. (1))

Рассмотрим теперь перемещение заряда по траектории ACB

(см. рис. 1). В этом случае работа однородного поля может быть представлена как сумма работ на участках
AC
и
CB
:
(~A_{ACB} = A_{AC} + A_{CB} = q cdot E cdot Delta x + 0 = q cdot E cdot Delta x)
(на участке CB

работа равна нулю, т.к. перемещение перпендикулярна силе (~vec F )). Как видно, работа поля такая же, как и при перемещении заряда по отрезку
AB
.

Не сложно доказать, что работа поля при перемещении заряда между точками AB

по любой траектории будет находиться все по той же формуле 1.

Таким образом,

работа по перемещению заряда в электростатическом поле не зависит от формы траектории, по которой двигался заряд
q
, а зависит только от начального и конечного положений заряда
.
Это утверждение справедливо и для неоднородного электростатического поля.

Найдем работу на замкнутой траектории ABCA

:
(~A_{ABCA} = A_{AB} + A_{BC} + A_{CA} = q cdot E cdot Delta x + 0 — q cdot E cdot Delta x = 0.)
Поле, работа сил которого не зависит от формы траектории и на замкнутой траектории равна нулю, называется потенциальным

или
консервативным
.

5.Понятие ротора

Поле по своей структуре может быть достаточно неоднородным. Циркуляция же не дает детальной характеристики поля. Следовательно, начнем стягивать контур интегрирования к какой-либо точке М

(уменьшать турбину). Циркуляция при этом будет стремиться к нулю, но и площадь, охваченная контуром, также будет стремиться к нулю. А их отношение дает конечное число.

Турбину можно ориентировать в пространстве тремя независимыми способами. Следовательно, таким способом можно получить 3 независимых числа, а три числа – это вектор, следовательно, образуется векторная характеристика поля, которая и называется ротором.

Ротор

– это локальная или дифференциальная характеристика.

Потенциал

Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система «заряд — электростатическое поле» обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:

(~A_{12} = -(W_{2} — W_{1}) = W_{1} — W_{2} . )

Сравнивая полученное выражение с уравнением 1, можно сделать вывод, что

(~W = -q cdot E cdot x, )

где x

— координата заряда на ось 0Х, направленную вдоль силовой линии (см. рис. 1). Так как координата заряда зависит от выбора системы отсчета, то и потенциальная энергия заряда так же зависит от выбора системы отсчета.

Если W

2 = 0, то в каждой точке электростатического поля потенциальная энергия заряда
q
0 равна работе, которая была бы совершена при перемещении заряда
q
0 из данной точки в точку с нулевой энергией.

Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q

. Будем помещать в некоторую точку этого поля различные пробные заряды
q
0. Потенциальная энергия их различна, но отношение (~dfrac{W}{q_0} = operatorname{const}) для данной точки поля и служит характеристикой поля, называемой
потенциалом
поля φ в данной точке.

Потенциал электростатического поля φ в данной точке пространства — скалярная физическая величина, равная отношению потенциальной энергии W
, которой обладает точечный заряд
q
в данной точке пространства, к величине этого заряда:

(~varphi = dfrac{W}{q} .)
Единицей потенциала в СИ является вольт

(В): 1 В = 1 Дж/Кл.

Потенциал — это энергетическая характеристика поля.

Свойства потенциала.

Потенциал, как и потенциальная энергия заряда, зависит от выбора системы отсчета (нулевого уровня). В технике
за нулевой потенциал выбирают потенциал поверхности Земли или проводника, соединенного с землей. Такой проводник называют
заземленным
. В
физике
за начало отсчета (нулевой уровень) потенциала (и потенциальной энергии) принимается любая точка, бесконечно удаленная от зарядов, создающих поле.

На расстоянии r
от точечного заряда
q
, создающего поле, потенциал определяется формулой

(~varphi = k cdot dfrac{q}{r}.)

Потенциал в любой точке поля, создаваемого положительным
зарядом
q
,
положителен
, а поля, создаваемого отрицательным зарядом, отрицателен: если
q
> 0, то φ > 0; если
q
< 0, то φ < 0.

Потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R
, в точке, находящейся на расстоянии
r
от центра сферы (~varphi = k cdot dfrac{q}{R}) при
r
≤
R
и (~varphi = k cdot dfrac{q}{r}) при
r
>
R
.

Принцип суперпозиции
: потенциал φ поля, созданного системой зарядов, в некоторой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:

(~varphi = varphi_1 + varphi_2 + varphi_3 + … = sum_{i=1}^n varphi_i .)
Зная потенциал φ поля в данной точке, можно рассчитать потенциальную энергию заряда q

0 помещенного в эту точку:
W
1 =
q
0⋅φ. Если положить, что вторая точка находится в бесконечности, т.е.
W
2 = 0, то
(~A_{1infty} = W_{1} = q_0 cdot varphi_1 .)
Потенциальная энергия заряда q

0 в данной точке поля будет равна работе сил электростатического поля по перемещению заряда
q
0 из данной точки в бесконечность. Из последней формулы имеем
(~varphi_1 = dfrac{A_{1infty}}{q_0}.)

Физический смысл потенциала
: потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в бесконечность.

Потенциальная энергия заряда q

0 помещенного в электростатическое поле точечного заряда
q
на расстоянии
r
от него,
(~W = k cdot dfrac{q cdot q_0}{r}.)

Если q
и
q
0 — одноименные заряды, то
W
> 0, если
q
и
q
0 — разные по знаку заряды, то
W
< 0.

Отметим, что по этой формуле можно рассчитать потенциальную энергию взаимодействия двух точечных зарядов, если за нулевое значение W
выбрано ее значение при
r
= ∞.

Пусть в некоторой области пространства существует векторное поле .

Циркуляцией вектора по произвольному замкнутому контуру L
называется следующий криволинейный интеграл:

Здесь — единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.

Существует соглашение, что положительное направление обхода контура (направление ) выбирается таким, чтобы область, охваченная контуром, оставалась при обходе слева.

Напомним, вкратце, как можно “сконструировать” криволинейный интеграл. Для этого нужно выбрать точку на контуре, показать в ней вектор , в этой же точке показать единичный вектор касательной, вычислить скалярное произведение , разбить контур на малые элементы, длину элемента обозначить , вычислить произведение ; проделать это для всех элементов контура; произвести суммирование результатов, устремляя элемент длины контура к нулю — перейти от суммирования к интегрированию.

Так же, как и поток, циркуляция является ещё одной характеристикой свойств векторного поля. А именно, циркуляция характеризует степень завихренности векторного поля.

Пример:

если в качестве «измерителя» циркуляции поля скоростей жидкости можно взять турбинку, то если она вращается, циркуляция не равна нулю.

Циркуляция

– это интегральная характеристика поля.

Разность потенциалов. Напряжение

Работа сил электростатического поля по перемещению заряда q

0 из точки
1
в точку
2
поля
(~A_{12} = W_{1} — W_{2} .)
Выразим потенциальную энергию через потенциалы поля в соответствующих точках:

(~W_{1} = q_0 cdot varphi_1 , W_{2} = q_0 cdot varphi_2 .)

Тогда

(~A_{12} = q_0 cdot (varphi_1 — varphi_2) .)

Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.

Из этой формулы разность потенциалов

(~varphi_1 — varphi_2 = dfrac{A_{12}}{q_0} .)

Разность потенциалов
— это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.

В СИ единицей разности потенциалов является вольт (В).

1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.

Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ1 — φ2 часто называют электрическим напряжением

между данными точками поля и обозначают
U
:
(~U = varphi_1 — varphi_2 .)

Напряжение
между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую.

Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах

1 эВ равен работе, совершаемой силами поля при перемещении электрона (е
= 1,6·10-19 Кл) между двумя точками, напряжение между которыми равно 1 В.

1 эВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж. 1 МэВ = 106 эВ = 1,6·10-13 Дж.

План:

1.Работа электрического поля.

2.Работа в поле точечного заряда.

3.Теорема о циркуляции.

4.Понятие о циркуляции.

5.Понятие ротора.

6.Формула Стокса.

7.Выражение для ротора в декартовой системе координат.

8.Циркуляция и ротор в электростатике.

9.Потенциальная энергия.

10.Разность потенциалов.

11.Единица разности потенциалов.

12.Потенциал точечного заряда.

Разность потенциалов и напряженность

Рассчитаем работу, совершаемую силами электростатического поля при перемещении электрического заряда q

0 из точки с потенциалом φ1 в точку с потенциалом φ2 однородного электрического поля.

С одной стороны работа сил поля (~A = q_0 cdot (varphi_1 — varphi_2)).

С другой стороны работа по перемещению заряда q

0 в однородном электростатическом поле (~A = q_0 cdot E cdot Delta x).

Приравнивая два выражения для работы, получим:

(~q_0 cdot (varphi_1 — varphi_2) = q_0 cdot E cdot Delta x, ;; E = dfrac{varphi_1 — varphi_2}{Delta x},)

где Δx

— проекция перемещения на силовую линию.

Эта формула выражает связь между напряженностью и разностью потенциалов однородного электростатического поля. На основании этой формулы можно установить единицу напряженности в СИ: вольт на метр (В/м).

Методы обнаружения

Органы чувств человека не воспринимают электрических полей. Поэтому мы не можем их увидеть, попробовать на вкус или определить по запаху. Единственное, что может ощутить человек – это выпрямление волос вдоль линий напряжённости. Наличие слабых воздействий мы просто не замечаем.

Обнаружить их можно через воздействие на мелкие кусочки бумаги, бузиновые шарики и т.п. Электрическое поле воздействует на электроскоп – его лепестки реагируют на такие воздействия.

Очень простой и эффективный метод обнаружения с помощью стрелки компаса. Она всегда располагается вдоль линий напряжённости.

Существуют очень чувствительные электронные приборы, с лёгкостью определяющие наличие электростатических полей.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 228-233.
Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 86-95.

Силы и их действие на заряженную частицу

На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее. Этой силой совершается работа по передвижению электрона.

Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.

Свойства силовых линий:

путешествуют с севера на юг;
не имеют взаимных пересечений.

Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни. То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом. Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.

Силовые линии демонстрируют:

направления электрических полей;
напряженность. Чем ближе линии, тем больше сила поля и наоборот.

Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.

Источник

Работа в электрическом поле. Потенциал

При перемещении пробного заряда q
в электрическом поле электрические
силы совершают работу. Эта работа при
малом перемещении

равна
(рис):

Работа электрических сил при малом
перемещении

заряда
q.

Электростатическое поле обладает важным
свойством:

Работа сил электростатического поля
при перемещении заряда из одной точки
поля в другую не зависит от формы
траектории, а определяется только
положением начальной и конечной точек
и величиной заряда.

Аналогичным свойством обладает и
гравитационное поле, и в этом нет ничего
удивительного, так как гравитационные
и кулоновские силы описываются одинаковыми
соотношениями.

Следствием независимости работы от
формы траектории является следующее
утверждение:

Работа сил электростатического поля
при перемещении заряда по любой замкнутой
траектории равна нулю.

Силовые поля, обладающие этим свойством,
называют потенциальными
или консервативными.

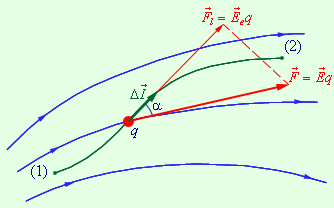
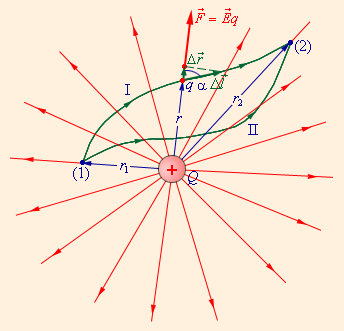
На рис. изображены силовые линии
кулоновского поля точечного заряда Q
и две различные траектории перемещения
пробного заряда q из начальной точки
(1) в конечную точку (2). На одной из
траекторий выделено малое перемещение

Работа
ΔA кулоновских сил на этом перемещении
равна

Таким образом, работа на малом перемещении
зависит только от расстояния r между
зарядами и его изменения Δr. Если
это выражение проинтегрировать на
интервале от r = r₁ до
r = r₂, то можно получить

Работа кулоновских сил при перемещении
заряда q зависит только от расстояний
r₁ и r₂ начальной и
конечной точек траектории.

Полученный результат не зависит от
формы траектории. На траекториях I и II,
изображенных на рис. 1.4.2, работы
кулоновских сил одинаковы. Если на одной
из траекторий изменить направление
перемещения заряда q на противоположное,
то работа изменит знак. Отсюда следует,
что на замкнутой траектории работа
кулоновских сил равна нулю.

Если электростатическое поле создается
совокупностью точечных зарядов Q_i,
то при перемещении пробного заряда q
работа A
результирующего поля в соответствии с
принципом суперпозиции будет складываться
из работ A_i
кулоновских полей точечных зарядов:

Так
как каждый член суммы A_i
не зависит от формы траектории, то и
полная работа A
результирующего поля не зависит от пути
и определяется только положением
начальной и конечной точек.

Свойство потенциальности электростатического
поля позволяет ввести понятие потенциальной
энергии заряда в
электрическом поле. Для этого в
пространстве выбирается некоторая
точка (0), и потенциальная энергия заряда
q, помещенного в
эту точку, принимается равной нулю.

Потенциальная энергия
заряда q,
помещенного в любую точку (1) пространства,
относительно фиксированной точки (0)
равна работе A₁₀,
которую совершит электрическое поле
при перемещении заряда q
из точки (1) в точку (0):

W_p1 = A₁₀.

(В электростатике энергию принято
обозначать буквой W,
так как буквой E
обозначают напряженность поля.)

Так же, как и в механике, потенциальная
энергия определена с точностью до
постоянной величины, зависящей от выбора
опорной точки (0). Такая неоднозначность
в определении потенциальной энергии
не приводит к каким-либо недоразумениям,
так как физический смысл имеет не сама
потенциальная энергия, а разность ее
значений в двух точках пространства.

Работа, совершаемая
электрическим полем при перемещении
точечного заряда q
из точки (1) в точку (2), равна разности
значений потенциальной энергии в этих
точках и не зависит от пути перемещения
заряда и от выбора точки (0).

A₁₂ = A₁₀ + A₀₂ = A₁₀ – A₂₀ = W_p1 – W_p2.

Потенциальная энергия заряда q,
помещенного в электрическое поле,
пропорциональна величине этого заряда.

Физическую величину,
равную отношению потенциальной энергии
электрического заряда в электростатическом
поле к величине этого заряда, называют
потенциалом
φ
электрического поля:

Потенциал φ является энергетической
характеристикой электростатического
поля.

Работа A₁₂
по перемещению электрического заряда
q из начальной
точки (1) в конечную точку (2) равна
произведению заряда на разность
потенциалов (φ₁ – φ₂)
начальной и конечной точек:

A₁₂ = W_p1 – W_p2 = qφ₁ – qφ₂ = q(φ₁ – φ₂).

В Международной системе единиц (СИ)
единицей потенциала является вольт
(В).

1 В = 1 Дж / 1 Кл.

Во многих задачах электростатики при
вычислении потенциалов за опорную точку
(0) удобно принять бесконечно удаленную
точку. В этом случае понятие потенциала
может быть определено следующим образом:

Потенциал поля в
данной точке пространства равен работе,
которую совершают электрические силы
при удалении единичного положительного
заряда из данной точки в бесконечность.

Потенциал φ_∞ поля точечного
заряда Q на
расстоянии r от
него относительно бесконечно удаленной
точки вычисляется следующим образом:

Как следует из теоремы Гаусса, эта же
формула выражает потенциал поля однородно
заряженного шара (или сферы) при r ≥ R,
где R – радиус шара.

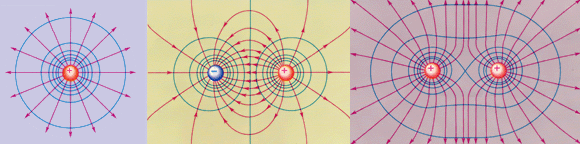
Для наглядного представления электрического
поля наряду с силовыми линиями используют
эквипотенциальные поверхности.

Поверхность, во всех точках которой
потенциал электрического поля имеет
одинаковые значения, называется
эквипотенциальной
поверхностью или поверхностью
равного потенциала.

Силовые линии электрического поля
всегда перпендикулярны эквипотенциальным
поверхностям.

Эквипотенциальные поверхности
кулоновского поля точечного заряда –
концентрические сферы. На рис.
представлены картины силовых линий и
эквипотенциальных поверхностей некоторых
простых электростатических полей.

Эквипотенциальные
поверхности (синие линии) и силовые
линии (красные линии) простых
электрических полей: a – точечный
заряд; b – электрический диполь; c –
два равных положительных заряда.

В случае однородного поля эквипотенциальные
поверхности представляют собой систему
параллельных плоскостей.

Если пробный заряд q совершил малое
перемещение

вдоль
силовой линии из точки (1) в точку (2),
то можно записать:

ΔA₁₂ = qEΔl = q(φ₁ – φ₂) = – qΔφ,

где Δφ = φ₁ – φ₂ –
изменение потенциала. Отсюда следует

Это соотношение в скалярной форме
выражает связь между напряженностью
поля и потенциалом. Здесь l –
координата вдоль силовой линии.

Из принципа суперпозиции напряженностей
полей, создаваемых электрическими
зарядами, следует принцип суперпозиции
для потенциалов:

φ = φ₁ + φ₂ + φ₃ + …

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Работа сил электрического поля. Напряжение

План урока

Работа электрического поля
Напряжение

Цели урока

Знать: формулы для расчета работы электрического поля; понятие напряжения; формулу напряжения; связь между работой электрических сил и напряжением
Уметь: проводить аналогию между работой силы тяжести и работой электрической силы; выводить формулу для расчета работы однородного электрического поля

Разминка

По какой формуле рассчитывается работа в механике?
Может ли электрическое поле совершить механическую работу?
Что общего между гравитационным полем Земли и электрическим полем?

Работа электрического поля

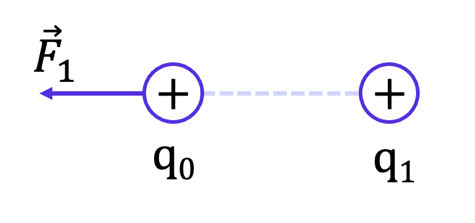
Рис. 1. Взаимодействие двух положительных зарядов

Рассмотрим систему, состоящую из двух положительных зарядов q0 и q1 (рис. 1). Нам уже известно, что сила Кулона, действующая на заряд q0, будет направлена от заряда q1, в нашем случае – влево.

Из механики нам известно, что работу можно найти по следующей формуле:

A=F·∆x,

где F – модуль постоянной силы, действующей на тело, ∆x – перемещение тела.

Если направления движения тела и действующей на него силы совпадают, то работа такой силы положительна.

Если же направления приложенной силы и движения тела противоположны, то работа такой силы отрицательна.

Соответственно, если заряд q0 перемещается влево, по направлению силы, то электрическая сила Fэл→ совершает положительную работу. Потенциальная энергия такой системы уменьшается.

В противном случае, если заряд q0 перемещается вправо, против направления действия силы, то электрическая сила совершает отрицательную работу.

Потенциальная энергия системы увеличивается, подобно энергии сжатой пружины.

Формула подразумевает действие постоянной силы, в приведенном примере сила, равная Fэл=E·q0 будет уменьшаться по мере удаления от заряда q1 вместе с модулем напряженности. Расчет работы электрического поля в данном случае будет очень трудоемок, поэтому мы рассмотрим работу однородного поля, в котором вектор напряженности не меняется E=const, следовательно, и значение силы также не будет меняться с течением времени.

Как вы уже знаете, однородное электрическое поле существует между двумя разноименно заряженными пластинами. В этом случае силу, действующую на пробный заряд q0, можно найти по формуле:

Fэл→=E→·q0.

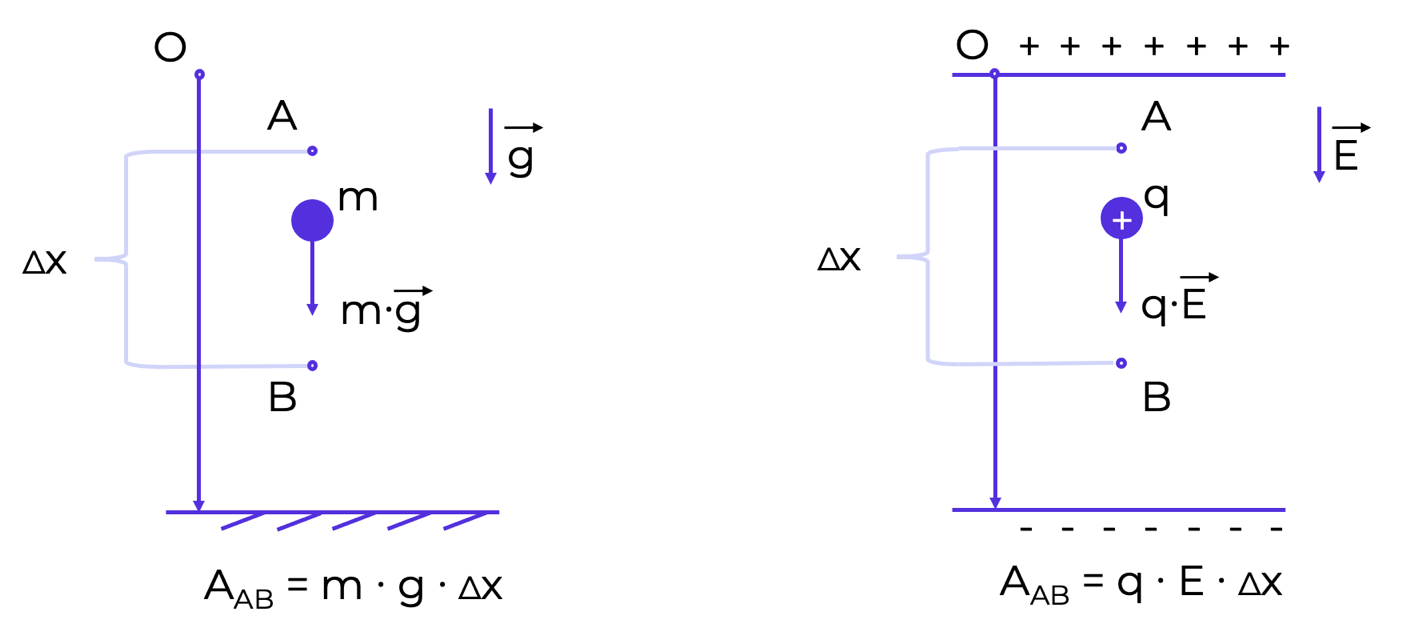
Проведем аналогию между однородным электрическим полем и гравитационным полем Земли. Известно, что сила тяжести находится по следующей формуле:

Fтяж→=m·g→.

Сила тяжести прямо пропорциональная массе тела m и сонаправлена с вектором ускорения свободного падения g→; электрическая сила прямо пропорциональна величине пробного заряда q и сонаправлена с вектором напряженности E→.

Сравним работу силы тяжести и работу электрической силы в случае, когда вектор напряженности направлен вертикально вниз (рис. 2).

Рис. 2. Сравнение работы силы тяжести и работы электрической силы при перемещении положительного заряда

Пусть тело массой m под действием силы тяжести перемещается из точки A в точку B. Тогда перемещение этого тела равно:

∆x=xB-xA.

В соответствии с формулами выше работа силы тяжести будет равна:

A=m·g·∆x.

Пусть теперь точечный положительный заряд q перемещается из точки A в точку B вдоль силовой линии электрического поля, то есть по направлению действия силы Fэл=q·E.

A=Fэл·∆x=E·q·∆x.

Если вместо положительного заряда q перемещается отрицательный заряд -q, то действующая на него электрическая сила будет направлена в сторону, противоположную перемещению. Поэтому работа электрической силы в этом случае будет отрицательна:

A=Fэл·∆x=-E·q·∆x.

Напряжение

Из последнего выражения видно, что работа электрического поля прямо пропорциональна величине заряда q. Отношение работы электрической силы к величине заряда называется напряжением:

U=Aq,

где U [В] – напряжение;
A [Дж] – работа электрического поля по перемещению заряда q₀;
q [Кл] – величина заряда.

Напряжение
– скалярная физическая величина, равная отношению работы сил электрического поля по перемещению точечного заряда q к величине этого заряда:

U=Aq.

В СИ единица измерения напряжения – вольт (В).

Если напряженность – силовая характеристика поля, то напряжение – это энергетическая характеристика электрического поля.

С одной стороны, при перемещении положительного заряда q по линии напряженности однородного поля на расстояние ∆x электрическая сила Fэл→ совершает работу, равную

A=Fэл·∆x=E·q·∆x.

С другой стороны, работа электрической силы поля может быть найдена по известному напряжению U между начальной и конечной точками перемещения:

A=q·U.

Приравнивая правые части выражений для работы, получаем, что напряжение U между двумя точками в однородном электрическом поле, расположенными на одной линии напряженности, равно произведению модуля вектора напряженности E→ поля на расстояние ∆x между этими точками:

U=E·∆x.

Отсюда для напряженности однородного электрического поля получаем выражение

E=U∆x.

Таким образом единицей измерения напряженности, кроме Н/Кл, также справедливо называть В/м.

Пример 1

Тело, двигаясь равномерно прямолинейно вдоль направления электрического поля со скоростью v = 15 м/с в течение 2 минут, совершило работу 7,2 кДж. Определить модуль вектора напряжённости электрического поля E, если заряд тела равен 4 Кл.

Решение

1. Запишем исходные данные:

v = 15 м/с; t = 2 мин = 120 с; A = 3,6 кДж = 3600 Дж; q = 4 Кл.

2. Запишем выражение для работы электрической силы:

A=E·q·∆x.

3. Поскольку заряд двигается вдоль направления электрического поля E→, то знак работы электрической силы будет иметь положительное значение.

4. Заряд двигался равномерно, значит его перемещение равно ∆x=v·t. Теперь перепишем формулу для работы электрического поля:

A=E·q·v·t.

5. Выразим напряжённость электрического поля из уравнения выше:

E=Aq·v·t=36004·15·120=0,5 Вм.

Ответ: E=0,5 Вм.

Итоги

Работу электрического поля напряженностью E по перемещению заряда q можно найти по следующей формуле: A=E·q·∆x.
Напряжение
– скалярная физическая величина, равная отношению работы сил электрического поля по перемещению точечного заряда q к величине этого заряда: U=Aq=E·∆x.
Напряжение не зависит от величины перемещаемого заряда q.
Напряжение – это энергетическая характеристика электрического поля.

Контрольные вопросы

1. Приведите пример, когда электрическое поле совершает отрицательную работу.
2. Как найти работу электрической силы?
3. От каких физических величин зависит напряжение?

Источник

From Wikipedia, the free encyclopedia

For other examples of «work» in physics, see Work (physics).

Electric field work is the work performed by an electric field on a charged particle in its vicinity. The particle located experiences an interaction with the electric field. The work per unit of charge is defined by moving a negligible test charge between two points, and is expressed as the difference in electric potential at those points. The work can be done, for example, by electrochemical devices (electrochemical cells) or different metals junctions^{[clarification needed]} generating an electromotive force.

Electric field work is formally equivalent to work by other force fields in physics,^[1] and the formalism for electrical work is identical to that of mechanical work.

Physical process[edit]

Particles that are free to move, if positively charged, normally tend towards regions of lower electric potential (net negative charge), while negatively charged particles tend to shift towards regions of higher potential (net positive charge).

Any movement of a positive charge into a region of higher potential requires external work to be done against the electric field, which is equal to the work that the electric field would do in moving that positive charge the same distance in the opposite direction. Similarly, it requires positive external work to transfer a negatively charged particle from a region of higher potential to a region of lower potential.

Kirchhoff’s voltage law, one of the most fundamental laws governing electrical and electronic circuits, tells us that the voltage gains and the drops in any electrical circuit always sum to zero.

The formalism for electric work has an equivalent format to that of mechanical work. The work per unit of charge, when moving a negligible test charge between two points, is defined as the voltage between those points.

${displaystyle W=Qint _{a}^{b}mathbf {E} cdot ,dmathbf {r} =Qint _{a}^{b}{frac {mathbf {F_{E}} }{Q}}cdot ,dmathbf {r} =int _{a}^{b}mathbf {F_{E}} cdot ,dmathbf {r} }$

where

Q is the electric charge of the particle

E is the electric field, which at a location is the force at that location divided by a unit (‘test’) charge

F_E is the Coulomb (electric) force

r is the displacement

is the dot product operator

Mathematical description[edit]

Given a charged object in empty space, Q+. To move q+ closer to Q+ (starting from ${displaystyle r_{0}=infty }$ , where the potential energy=0, for convenience), we would have to apply an external force against the Coulomb field and positive work would be performed. Mathematically, using the definition of a conservative force, we know that we can relate this force to a potential energy gradient as:

${displaystyle -{frac {partial U}{partial mathbf {r} }}=mathbf {F} _{ext}}$

Where U(r) is the potential energy of q+ at a distance r from the source Q. So, integrating and using Coulomb’s Law for the force:

${displaystyle U(r)=Delta U=-int _{r_{0}}^{r}mathbf {F} _{ext}cdot ,dmathbf {r} =-int _{r_{0}}^{r}{frac {1}{4pi varepsilon _{0}}}{frac {q_{1}q_{2}}{mathbf {r^{2}} }}cdot ,dmathbf {r} ={frac {q_{1}q_{2}}{4pi varepsilon _{0}}}left({frac {1}{r_{0}}}-{frac {1}{r}}right)=-{frac {q_{1}q_{2}}{4pi varepsilon _{0}}}{frac {1}{r}}}$

Now, use the relationship

To show that the external work done to move a point charge q+ from infinity to a distance r is:

${displaystyle W_{ext}={frac {q_{1}q_{2}}{4pi varepsilon _{0}}}{frac {1}{r}}}$

This could have been obtained equally by using the definition of W and integrating F with respect to r, which will prove the above relationship.

In the example both charges are positive; this equation is applicable to any charge configuration (as the product of the charges will be either positive or negative according to their (dis)similarity).
If one of the charges were to be negative in the earlier example, the work taken to wrench that charge away to infinity would be exactly the same as the work needed in the earlier example to push that charge back to that same position.
This is easy to see mathematically, as reversing the boundaries of integration reverses the sign.

Uniform electric field[edit]

Where the electric field is constant (i.e. not a function of displacement, r), the work equation simplifies to:

$W=Q({mathbf {E}}cdot ,{mathbf {r}})={mathbf {F_{E}}}cdot ,{mathbf {r}}$

or ‘force times distance’ (times the cosine of the angle between them).

Electric power[edit]

The electric power is the rate of energy transferred in an electric circuit. As a partial derivative, it is expressed as the change of work over time:

$P={frac {partial W}{partial t}}={frac {partial QV}{partial t}}$

where V is the voltage. Work is defined by:

delta W={mathbf {F}}cdot {mathbf {v}}delta t,

Therefore

${frac {partial W}{partial t}}={mathbf {F_{E}}}cdot ,{mathbf {v}}$

References[edit]

^ Debora M. Katz (1 January 2016). Physics for Scientists and Engineers: Foundations and Connections. Cengage Learning. pp. 1088–. ISBN 978-1-337-02634-5.

Источник