Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
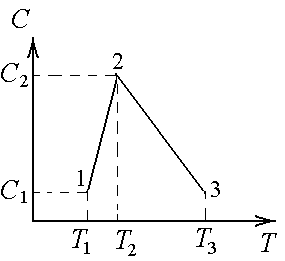
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
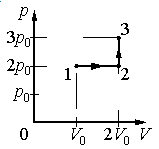
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k
Работа идеального газа
равна
.
При расширении работа газа
положительна, при сжатии – отрицательна.
Чтобы получить функцию
давления в зависимости от объема, надо
использовать совместно с уравнением
процесса уравнение Менделеева-Клапейрона
4-1. В воздушном шарике
находится одноатомный идеальный газ.
Газ расширяется от объема
до объема
,
при этом его давление меняется по закону
а)
;
б)
;
в)
;
г)
.
Найти работу (в МДж),
совершенную газом в этом процессе.
p0
= 105
Па;
=
1 м3;
=2
м3.
Ответы: а) 0,15 МДж; б) 0,233 МДж;
в) 0,375 МДж; г) 0,62 МДж
4-2. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема
до объема
,
при этом его температура меняется по
закону
а)
;
б)
;
в)
;
г)
Найти работу (в кДж),
совершенную газом в этом процессе.
Универсальная газовая постоянная
.
T0
= 300 K;
=
1 м3;
=2
м3.
Ответы: а) 26,1 кДж; б) 45,2 кДж;
в) 79,4 кДж; г) 141 кДж
4-3. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема
до объема
,
при этом его объем меняется по закону
а)
;
б)
;
в)
;
г)
Найти работу (в кДж),
совершенную газом в этом процессе.
Универсальная газовая постоянная
.
= 300 K;
=
1 м3;
=2
м3.
Ответы: а) 3,74 кДж; б) 5,82 кДж;
в) 9,35 кДж; г) 15,5 кДж
4-4. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема
до объема
,
при этом его давление меняется по закону
.
Найти работу (в МДж), совершенную газом
в этом процессе. Универсальная газовая
постоянная
.
= 300 K;
= 105
Па;
=
1 м3;
=2
м3.
Ответ: 6,02 МДж
4-5. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема
до объема
,
при этом его температура меняется по
закону
.
Найти работу (в МДж), совершенную газом
в этом процессе. Универсальная газовая
постоянная
.
= 300 K;
= 105
Па;
=
1 м3;
=2
м3.
Ответ: 6,02 МДж
4
-6э.
Идеальный газ совершает циклический
процесс 1-2-3-1, как показано на рисунке,
где процессы 2-3 — изохорический, а 3-1 —
изотермический. Площадь
фигуры 1-2-3 равна 10 Дж, а площадь
фигуры 1-3-В-А равна 15 Дж.
В процессе 3-1 газ отдал
окружающей среде тепло…
Ответ: 15 Дж
5. Теплоемкость.
Теплоемкость
газа равна
– теплота, необходимая для нагревания
тела (газа) на один Кельвин.
Зная теплоемкость, можно
определить теплоту, переданную газу
при нагревании:
Если задана зависимость
теплоемкости от температуры в виде
графика, то теплота есть площадь
под кривой
.
Изменение
внутренней энергии
идеального газа равна
,
где
– число степеней свободы молекулы. При
не очень высокой и не очень низкой
температуре (когда возбуждены вращательные
степени свободы, но не возбуждены
колебательные степени свободы) i
= 3 для одноатомного
газа, i
=5 для двухатомного
газа, i
= 6 для трех- и
(более)-атомного газа.
Первое начало термодинамики:
теплота, переданная газу
от нагревателя, идет на увеличение
внутренней энергии газа и на совершение
эти газом работы. Если внутренняя энергия
газа при этом уменьшается, то
.
Политропический процесс
– процесс с постоянной теплоемкостью.
5-1. Теплоемкость газа зависит
от температуры по закону
а)
;
б)
;
в)
;
г)
.
Найти тепло, полученное
газом, если его температура увеличилась
с
до
.
=1
Дж/К;
=300
К;
.
Ответы: а) 450 Дж; б) 1125 Дж; в)
3150 Дж; г) 9,56 кДж
5-2. Теплоемкость газа зависит
от температуры по закону
а)
;
б)
;
в)
;
г)
При изменении температуры
газа от
до
им была совершена работа А.
Найти изменение внутренней энергии
газа.
=1
Дж/К;
=300
К;
;
А =
100 Дж.
Ответы: а) 600 Дж; б) 1760 Дж; в)
5,39 кДж; г) 16,9 кДж
5-3. Теплоемкость одного моля
идеального одноатомного
газа зависит от температуры по закону
а)
;
б)
.
Найти работу, совершенную
газом, при изменении температуры газа
от
до
.
Универсальная газовая постоянная R
= 8,3 Дж/мольК;
=1
Дж/К;
=300
К;
.
Ответы: а) –3285 Дж; б) –2334 Дж
5-4. Теплоемкость одного моля
идеального двухатомного
газа зависит от температуры по закону
а)
;
б) .
Найти работу, совершенную
газом, при изменении температуры газа
от
до
.
Универсальная газовая постоянная R
= 8,3 Дж/моль×К;
=1
Дж/К;
=300
К;
.
Ответы: а) – 5775 Дж; б) – 4824
Дж
5-5. Теплоемкость одного моля
идеального трехатомного
газа зависит от температуры по закону
а)
;
б)
Найти работу, совершенную
газом, при изменении температуры газа
от
до
.
Универсальная газовая постоянная R
= 8,3 Дж/моль×К;
=1
Дж/К;
=300
К;
.
Ответы: а) – 7020 Дж; б) – 6069
Дж
5-6. Один моль идеального а)
одноатомного; б) двухатомного; в)
трехатомного газа совершает политропический
процесс. При этом его температура
увеличивается от
до
,
и газ совершает работу А.
Найти теплоемкость газа. Универсальная
газовая постоянная
.
=300
К;
;
А =
100 Дж.
Ответы: а) 12,8 Дж/К; б) 21,1 Дж/К;
в) 25,3 Дж/К
5-7. Один моль идеального а)
одноатомного; б) двухатомного ; в)
трехатомного газа совершает политропический
процесс с теплоемкостью С.
При этом его температура увеличивается
на
,
и газ совершает работу А.
Найти
.
Универсальная газовая постоянная
.
С = 30
Дж/К; А
= 100 Дж.
Ответы: а) 5,7 К; б) 10,8 К; в) 19,7
К
5-8. Один моль идеального а)
одноатомного; б) двухатомного; в)
трехатомного газа совершает политропический
процесс с теплоемкостью С.
При этом его температура увеличивается
на
,
и газ совершает работу А.
Найти А.
Универсальная газовая постоянная
.
С = 30
Дж/К;
= 10 К.
Ответы: а) 175 Дж; б) 92,3 Дж; в)
50,7 Дж
5
-9.
Идеальный газ совершает процесс 1–2–3.
Его теплоемкость зависит от температуры,
как показано на графике.
T1
= 600 К; T2
= 900 К; Т3
= 1800 К.
С1
= 1 Дж/К; С2
= 5 Дж/К.
Найти
а) тепло, полученное газом
в этом процессе.
б) Во сколько раз тепло,
полученное на участке 2–3 больше тепла,
полученного на участке 1–2.
в) На сколько джоулей тепло,
полученное на участке 2–3 больше тепла,
полученного на участке 1–2.
Ответы: а) 3600 Дж; б) в 3 раза; в) 1800 Дж

5-10э.
Молярные теплоемкости азота в процессах
и
равны
и
соответственно. Их отношение
равно: а)
б)
в)
г)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023