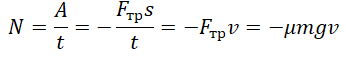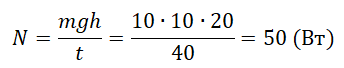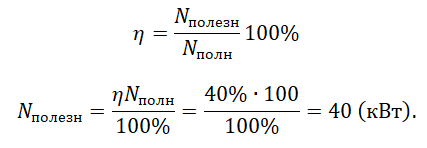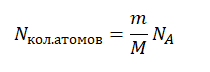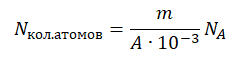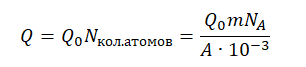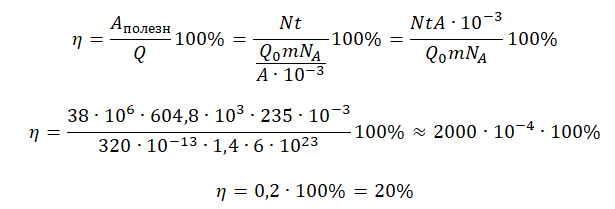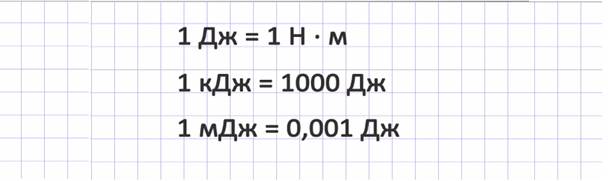Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна: |
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому: |
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость: |
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения: |
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
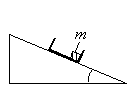
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 12k
Совершённая работа равна изменению энергии, потраченной на совершение работы.
Величину работы можно определить, вычитая из конечного значения энергии начальное значение энергии.
, где A — работа (Дж); E — энергия (Дж).
Работу, как и энергию, измеряют в джоулях (Дж).
Если энергия тела увеличивается, тогда общая совершённая работа является положительной.
Пример:
Когда автомобиль начинает двигаться, его кинетическая энергия увеличивается. Значит, двигатель автомобиля совершает положительную работу.
Если энергия тела уменьшается, тогда общая совершённая работа является отрицательной.
Пример:
Когда автомобиль свободно катится по горизонтальной поверхности, его скорость и кинетическая энергия уменьшаются. Значит, сила сопротивления совершает отрицательную работу.
В физике рассматривают физическую работу, которая связана с перемещением тел.
Если при прямолинейном движении на тело действует неизменная сила, направленная в сторону движения тела, тогда работа, произведённая приложенной силой, равна произведению величины силы на величину проделанного перемещения.
Если к телу приложена сила под вертикальным углом к направлению движения тела, как это показано на рисунке, тогда величина совершённой работы зависит от:
1) величины приложенной силы (F), которая совершает работу;
2) расстояния (l), на которое перемещается тело;
3) угла (α) между направлением действия силы и направлением движения тела.
Работа определяется по формуле: A=F⋅l⋅cosα.
Рис. (1). Под углом
Обрати внимание!
Если сила направлена параллельно направлению перемещения, тогда угол (α = 0), а (косинус) угла (α) равен (1). В этом случае формула упрощается:
A=F⋅l
.
Если проделанный путь является прямолинейным, тогда вместо пути (l) можно использовать перемещение (s).
В этом случае формула для расчёта работы приобретает такой вид:
A=F⋅s
.
На трёх рисунках изображены случаи, когда направление силы и направление движения тела совпадают.
1) Действие силы и направление движения тела направлены горизонтально. Например, автомобиль едет по прямому пути, и сила тяги автомобиля приложена в том же направлении.
Рис. (2). Параллельно
2) Действие силы и направление движения тела направлены под одинаковым углом наклона по отношению к горизонту. Например, автомобиль едет в гору.
Рис.(3). Движение «в гору»
3) Действие силы и направление движения тела направлены вертикально. Например, груз поднимается вверх, и сила упругости троса тоже направлена вверх. В этом случае величину совершённой работы можно рассчитать также по формуле
A=m⋅g⋅h
, где
(m) — масса тела, (g) — ускорение свободного падения,
(h) — высота подъёма тела над поверхностью земли.
Рис. (4). Движение вверх
Обрати внимание!
Если направление действия силы противоположно направлению движения, тогда совершаемая этой силой работа отрицательна.
Работа отрицательна, так как функция (косинус) в интервале значений угла (90° — 180°) является отрицательной.
Таким образом, любая работа, совершённая силой трения или сопротивления, является отрицательной.
Пример:
Когда автомобиль едет с равномерной скоростью по прямой дороге, как это показано на рисунке, работа силы тяги автомобиля является положительной, а работа силы сопротивления равна по величине, но является отрицательной. В результате этого кинетическая и потенциальная энергия автомобиля остаются неизменными.
Если сила направлена прямо противоположно направлению движения, тогда работу вычисляют по формуле:
A=−F⋅l
.
Рис. (5). Автомобиль
Источники:
Рис. 1. Под углом. © ЯКласс.
Рис. 2. Параллельно. © ЯКласс.
Рис. 3. Движение «в гору». © ЯКласс.
Рис. 4. Движение вверх. © ЯКласс.
Рис. 5. Автомобиль. © ЯКласс.
Содержание:
- § 1 Механическая работа
- § 2 Решение задач на определение механической работы
- § 3 Краткий итог урока
§ 1 Механическая работа
В этом уроке мы рассмотрим новую физическую величину – механическую работу, изучим условия совершения механической работы и единицы ее измерения.
Мы в жизни часто используем слово «работа». Программист сидит за
компьютером – это его работа, работают станок, холодильник, телевизор, работает строитель, работает инженер. Словом «работа» мы выражаем всякое полезное действие человека или устройства. В физике термин «работа» имеет несколько иной смысл. Рассмотрим примеры.
Лошадь тянет телегу, действуя на нее с некоторой силой – силой тяги, которую обозначим Fтяги. Телега движется по направлению силы тяги лошади. Говорят, что сила тяги совершает механическую работу по перемещению телеги.
Механическая работа (или работа силы над телом) – это скалярная физическая величина, равная произведению модуля силы на путь, пройденный телом вдоль направления этой силы.
Механическая работа обозначается строчной буквой «А». По определению формула работы запишется так:
В честь английского ученого Джеймса Джоуля единица измерения работы получила название Джоуль.
За 1 Джоуль принята работа, совершаемая силой 1 Ньютон на пути, равном 1 метру: 1 Дж = 1 Н · м.
Кратные единицы измерения:
В зависимости от направления действующей силы механическая работа может быть положительной и отрицательной.
Если направление силы совпадает с направлением движения тела, то работу силы считают положительной.
Например, лошадь тянет телегу (см. рис.) и совершает положительную работу:
камень падает (см. рис.) – сила тяжести совершает положительную работу:
выстрелили из лука (см. рис.) – сила упругости натянутой тетивы совершает положительную работу:
Если направление силы противоположно направлению движения тела, то работу силы считают отрицательной.
Например, сила трения скольжения совершает отрицательную работу, так как она направлена противоположно движению и тормозит движение тела:
А = – Fтрения · s.
Если направление силы перпендикулярно направлению движения тела, то работа этой силы равна нулю.
Например, сила давления человека, сидящего на телеге (см. рис.), перпендикулярна направлению движения телеги, телега под действием этой силы не перемещается, и поэтому работа силы давления равна нулю.
Если тело под действием силы не движется, то работа также равна нулю.
На гирю, подвешенную к нити, действует сила тяжести, но гиря не движется, значит, работа силы тяжести равна нулю (рис. 2).
Работа равна нулю и в том случае, если тело движется по инерции, то есть на него не действуют силы. Тогда в формуле работы А = F· sсила равна нулю, следовательно, работа равна нулю.
Итак, механическая работа совершается только в том случае, если на тело действует сила, и тело под действием этой силы движется.
§ 2 Решение задач на определение механической работы
Рассмотрим решение задач на определение механической работы.
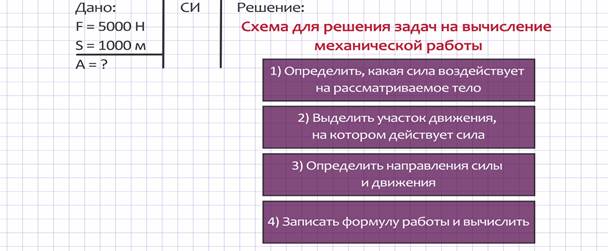
Задача 1. Буксирный катер тянет баржу с одного причала на другой, действуя с силой 5000 Н. Расстояние между причалами составляет 1000 м. Вычислить работу, совершаемую катером.
Запишем условие задачи: нам известна сила F = 5000 Н. Известно расстояние, на которое перемещается баржа: s =1000 м. Требуется найти работу.
Решение задач на вычисление механической работы будем проводить по определенной схеме.
1)Определим, какая сила воздействует на рассматриваемое тело. В этой задаче катер действует с силой 5000 Н на баржу, следовательно, работу совершает сила тяги катера.
2)Выделим участок движения, на котором действует сила: баржа перемещается от одного причала до другого на 1000 м.
3)Определим направления силы и движения: баржа движется в сторону действующей силы тяги, значит, работа, совершаемая силой тяги, положительная.
4) Запишем формулу работы и вычислим:
А = Fтяги · s = 5000 Н · 1000 м = 5000000 Н·м = 5000000 Дж = 5000 кДж.
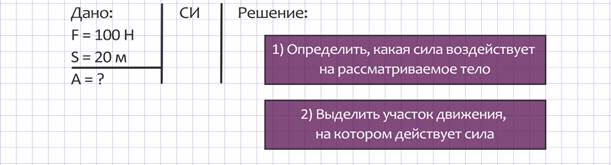
Задача 2. Хоккеист ударил по шайбе с силой 100 Н. Шайба, пройдя по льду путь 20 м, влетела в ворота противника. Найти механическую работу, совершенную хоккеистом.
Условие задачи: сила F = 100 Н, путь s = 20 м. Найти работу А.
Рассмотрим решение по схеме.
1. Определим, какая сила воздействует на рассматриваемое тело: хоккеист ударил по шайбе с силой 100 Н.
2. Выделим участок движения, на котором действует сила: сила хоккеиста действует только на том участке, где лежала шайба в момент удара, дальше сила удара не действует, шайба движется по инерции.
Так как путь, пройденный шайбой в момент удара, равен нулю, то мы можем сделать вывод, что работа, совершенная силой удара, равна нулю.
Итак, при решении задач на расчет механической работы нужно установить, какая сила совершает работу, какой путь проходит тело под действием этой силы, определить направление действующей силы и направление движения.
§ 3 Краткий итог урока
Механическая работ – это скалярная физическая величина, равная произведению модуля силы на путь, пройденный телом вдоль направления этой силы.
Формула для вычисления работы: А = F · s
Единица измерения работы: 1 Дж = 1 Н · м
Механическая работа положительна, если направление силы совпадает с направлением движения.
Работа отрицательна, если направление силы противоположно направлению движения.
Работа равна нулю, если направление силы перпендикулярно направлению движения, или если тело движется по инерции, или перемещение тела под действием силы равно нулю.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. — М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс — М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
План урока:
Механическая работа. Что характеризует мощность?
Какие бывают несложные механизмы. Как уравновесить рычаг?
Момент силы. Простые механизмы в природе, технике и быту
Правило механики «на вес золота»
КПД – коэффициент полезного действия
Механическая работа. Что характеризует мощность?
Исторически впервые термин «работа» придуман французом Ж. Понселе. Вначале ученый связал работу с каждодневной жизнедеятельностью человека: «работа врача», «вернулся с работы», «устроился на работу», «тяжелая работа». К физике это относилось лишь потому, что идти на работу или работать – это значит совершать какое-то передвижение. Затем Понселе связал работу с силой и дал название «механическая работа»:
Источник
А вот в науке механическая работа – это понятие, формируемое по правилам физики.
Пусть непрерывная сила F переместила тело в своем направлении на расстояние s. Эта сила совершила механическую работу, так как она переместила тело.
В физике принято обозначать работу буквой А. Тогда:
Источник
Для вычисления работы возможен один из вариантов:
Отсюда вытекает вывод, что для осуществления механической работы необходимы два одновременно выполняемых условия: 1) сила и 2) перемещение, осуществляемое именно этой силой.
Например, сила тяги какого-нибудь двигателя, сила давления, сила тяжести могут совершать и положительную и отрицательную работы:
Источник
Источник
При движении по какой-то поверхности возникает сила трения, например, мотоцикл едет по дороге, санки катятся по снегу. Воздух оказывает сопротивление спускающемуся парашютисту. Направлены силы трения и сопротивления всегда против движения. Получается, что движение тела в одну сторону, а направление силы – в другую. В этих случаях работа, совершаемая такими силами, отрицательная. В приведенных примерах сила тяги мотоцикла; сила тяги ребенка, который тащит санки; сила тяжести, действующая на парашютиста совершают положительную работу.
Всегда направлены против движения — силы сопротивления и трения. Совершаемые ими работы — отрицательны.
А = 0 в следующих случаях:
Источник
Два случая нулевой работы понять не трудно. Например, человек пытается сдвинуть тяжелый камень, толкает его с большой силой, а камень не перемещается. Нет перемещения, нет и работы этой силы. Движение по инерции — есть перемещение, но без действия сил, опять работа равна нулю.
В случае с перпендикулярностью дело обстоит следующим образом. Например, рабочий толкает тележку по дороге. Сила, которую он прилагает к грузу, направлена горизонтально, и тележка движется горизонтально в направлении именно этой силы – есть положительная работа. Но на тележку оказывает влияние и сила тяжести. Сила тяжести перпендикулярна дороге, и в ее направлении тележка не движется. Значит, работа силы тяжести равна 0. У перемещения и сила должно быть одно направление.
Про перпендикулярны надо подробнее
На уроке физкультуры дистанцию в 100 м пробежали все семиклассники. Они совершили одинаковую работу, но за различное время. Новое понятие физики, определяющее это условие – мощность.
Источник
Мощность — это тоже работа, но совершаемая за единицу времени. Например, за 8 с выполнена работа в 200 Дж, значит, за 1 с совершается 25 Дж работы (200 Дж : 8 с = 25 Дж).
Итак,
Источник
Здесь можно провести аналогию со скоростью. Скорость – путь в единицу времени, мощность – это работа в единицу времени. 2 м/с означает, что за каждую секунду тело проходит путь 2 м. 2 Вт – это значит, что за 1 с совершается работа 2 Дж.
Для различных машин, простых и сложных механизмов и самого человека мощность — очень нужная характеристика. Численные ее значения различны. Например, сердечная мощность у взрослого человека — 2,2 Вт, а двигатели в ракетостроении достигают мощности десятков миллионов киловатт.
Сравнимы ли мощность простого неспортивного человека и одна полная лошадиная сила?
Ученые считают: мощность человека меньше лошадиной силы (при размеренной работе) в 10 раз, т.е. равна 70-80 Вт. Однако в некоторых ситуациях человек кратковременно показывает очень высокую мощность. Быстро пробежав по лестнице за 1 с 6 ступенек (1,2 м), взрослый человек (70 кг) проделывает работу 840 Дж. Это как раз его мощность 840 Вт, а 1 л.с. = 735,5 Вт. Человек в этом случае мощнее лошади (конечно, речь не о том, кто сильнее).
Источник
С 1980 года 1 л. с. как единица измерения официально отменена, но используется и сейчас. Мощности двигателей обычно указываются в кВт.
Какие бывают несложные механизмы. Как уравновесить рычаг?
Сила мускулатуры человека небезгранична. Чтобы облегчить нагрузки на мышцы, издавна человек пытается внедрить в свою деятельность различные приспособления, устройства, несложные механизмы. Простых механизмов сконструировано довольно много. Самые распространенные:
Источник
Архимед в древности разработал немалое количество механических устройств. Он же выдвинул и теорию рычага. Рычаг – жесткое тело с закрепленной опорой, способное свободно поворачиваться около этой опоры.
Как и у любого устройства или приспособления, у рычага есть свои характеристики. Это:
- ось вращения (определяется точкой опоры);
- левое плечо и правое плечо – это отрезки, соединяющие линии сил и точку опоры;
- силы, прилагаемые с одной стороны от опоры или по разные стороны от нее.
Буквой О на рисунке отмечена точка опоры самого простейшего лабораторного рычага, отрезок ОА является плечом силы F1, отрезок ОВ – это плечо силы F2.
По расположению оси вращения применяются рычаги двух видов:
Источник
Рычаг дает возможность выиграть в силе. Это означает, что рычаг помогает заменить «неподъемную» силу, которой порой не хватает, на значительно меньшую. Но просто так ничего не бывает: выигрыш в силе — проигрыш в расстоянии.
По сути это равенство выражает условие равновесия рычага:
Отношение сил обратно пропорционально отношению плеч сил
Условие разрешает выигрывать в силе теоретически сколько угодно, но в действительности так не бывает. Плечо не бывает очень длинным. В свои времена Архимед выразил мысль о получении бесконечного выигрыша в силе фразой:
Пусть гениальный Архимед нашел искомую опору и сделал крепкий рычаг. Масса Земли 6 ∙ 1024 кг, поднять тело в 50 — 60 кг обычный человек в состоянии. Получается, для смещения хотя бы на 1 мм Земли, Архимеду потребовалось бы прошагать путь в 1017 км. Такие расчеты – хорошая демонстрация, каковы масштабы «проигрыша» в расстоянии.
Момент силы. Простые механизмы в природе, технике и быту
Из пропорции F2/F1 = l1/l2 получается равенство F1 ∙ l1 = F2∙ l2. Используя его, П.Вариньон (французский ученый) ввел первое определение момента силы:
Источник
Момент силы – это одна из величин, полученных путем математических преобразований. Использовали основное свойство пропорции F2/F1 = l1/l2, получили новое равенство F1 ∙ l1 = F2∙ l2. Слева и справа произведения одинаковых физических величин, только индексы разные. Слева — первая сила и ее плечо, справа — вторая сила и ее плечо. Назвали такое произведение моментом силы.
Если к телу приложены две силы, одна поворачивает тело по часовой стрелке, а другая – против, то для соблюдения равновесия нужно равенство:
Правило моментов соблюдается для произвольного жесткого тела, у которого зафиксирована ось вращения. Пусть тело произвольной формы имеет возможность вращаться (на рис. т.О обозначает ось). Плечом силы d здесь выступает расстояние от линии этой силы до оси. На тело может действовать несколько сил (необязательно две).
Источник
Из определения момента F ∙ l = M даже незначительная сила может дать большой вращающий момент, если взять достаточно большое плечо. Это условие часто применяют в технических и бытовых ситуациях. Расширенная рукоятка ключей, штопоров и отверток, удлиненные ручки гаечных ключей, вытянутые ручки ножниц по металлу – в этих устройствах длинные плечи.
Во многих отраслях деятельности человек издавна не обходится без использования рычагов. Это – технические устройства, механизмы, строительство.
Источник
Природа также создала много примеров рычагов. Самый замечательный из них – человеческая рука.
Источник
Чтобы удержать в руке тело, нужно уравновесить силу тяжести F2 и мышечную силу руки F1.
Источник
Интересен и такой пример природы. «Рычажный механизм» внутри цветка шалфея «загружает» шмелей пыльцой. Шмель, приземлившись на губу цветка (шалфей – семейство губоцветных), проникает внутрь за нектаром. У входа в цветок находятся две тычинки[1]. Они преграждают путь шмелю. Тычинки по внешнему виду напоминают рычаг. Мелкая часть каждой тычинки представляет одно плечо рычага. Находится это плечо снизу. Другое плечо рычага – это длинная верхняя часть тычинки. На ней раскачивается пыльник[2].
Шмель, залезая в цветок, давит на нижнее, короткое, плечо. Сверху длинное плечо наклоняется, и пыльник смазывает пыльцой спинку насекомого. А дальше шмель садится на следующий цветок. Спинка зацепляется за рыльце пестика[3] другого цветка. Рыльце легко задеть, так как оно наклонено вниз. Пыльца попадает внутрь пестика. Таким образом происходит опыление шалфея насекомыми.
Простые механизмы: блок и ворот – это виды рычагов.
Ворот — по сути бревно, способное вращаться вместе со своей осью. К оси крепится ручка, держась за которую можно осуществлять вращение. Как простой механизм ворот часто применяют при подъеме тяжелых грузов с глубины.
Источник
Чтобы увидеть в блоке рычаг, нужно мысленно диаметрально провести через центр блока отрезок (на рисунке отрезок АВ). Тогда l1 и l2 будут плечами приложенных к тросу сил.
Источник
Плечи сил F1 и F2 при равновесии одинаковы, значит и силы тоже одинаковы. Неподвижный блок выиграть в силе не может.
Источник
Плечо l1 больше плеча l2 в 2 раза, то есть l1 = 2l2.
Тогда равенство F1 ∙ l1 = F2∙ l2 запишется так: F1 ∙ 2l2 = F2∙ l2 (вместо l1 подставляем 2l2). Слева и справа есть одинаковый множитель l1. на него можно сократить обе части равенства. Получается, что F1 ∙ 2 = F2. Иначе F2 = 2 F1
Из условия равновесия сила F1 меньше силы F2 в 2 раза. Подвижный блок в 2 раза выигрывает в силе.
Часто тяжелые тела поднимают по наклонной плоскости. Работа получается больше, но зато выходит выигрыш в силе. Разделив длину наклонной плоскости на высоту, возможно рассчитать этот выигрыш. В данном случае при условии незначительного трения это будет довольно приближенная оценка.
Источник
Привычная лестница – пример наклонной плоскости:
Источник
По вертикальной лестнице труднее подниматься. По наклонной лестнице подниматься легче, но она длиннее.
Винты и винтообразные устройства, клинообразные приспособления – часто применяемые разновидности наклонной плоскости. Винт — это накрученная на ось наклонная плоскость. Клин – две наклонные плоскости, объединенные в призму[4].
Винт Источник
Клин Источник
Правило механики «на вес золота»
Используя разнообразные механические приспособления и устройства, люди облегчают себе труд, уменьшая физическую силу. Уменьшить работу эти механизмы не в состоянии. Если в механизмах применяется сила уменьшенная, то приходится увеличивать расстояние (длину наклонной плоскости, плечо рычага). К такому правилу пришел Герон Александрийский. По своей значимости это правило стало в механике «золотым правилом»:
Источник
Источник
Данное правило без учета силы тяжести и силы трения самих приспособлений и деталей механизмов является довольно приближенным.
КПД – коэффициент полезного действия
Прежде нужно разобраться в словах «полезное действие». Вот пример. Картофель, собранный для хранения на семена, фермер засыпает из ведер в большие контейнеры. Погрузка картофеля ведрами является полной (иначе совершенной) работой. Она состоит из подъема ведер и самого картофеля. Подъем картофеля – это работа полезная, а заполнение и поднятие ведер – бесполезная. Ведра нужно поднимать, опускать, наполнять картофелем.
Полная работа, конечно же, превышает полезную. Находя, как относится полезная работа к полной (совершенной работе), получают величину, называемую коэффициентом полезного действия (КПД). Часто КПД вычисляется в процентах. Для обозначения используется буква η (эта) из греческого алфавита.
η = (Аполезная/Аполная) ∙ 100 %
КПД можно рассчитать следующим образом. Пусть дана наклонная плоскость:
Источник
Схематически на рисунке это выглядит так:
Источник
Работая над конструкциями и создавая машины, изобретатели стараются повысить КПД. Уменьшая массу работающих и движущихся частей в устройствах, трение контактирующих деталей, конструкторы добиваются неплохих результатов.
Нужно отметить, что нет механизмов, дающих КПД в 100%. В настоящее время уже есть машины и механизмы с КПД около 98-99 %, но создать работающее устройство со 100% — м КПД невозможно.
Словарь
1. Тычинка – мужская составляющая в строении цветка. Содержит пыльник с пыльцой, тычиночную нить.
2. Пыльник – часть тычинки, где созревает пыльца.
3. Пестик – часть цветка, представляющая женский орган с рыльцем, столбиком и завязью.
4. Призма – физическое тело, многогранник с двумя параллельными основаниями и боковыми гранями – параллелограммами. (Клин – треугольная призма, в основаниях которой лежат треугольники).