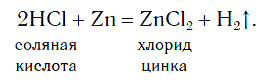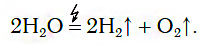В уроке 26 «Получение водорода и его применение» из курса «Химия для чайников» узнаем о получении водорода в лабораториях и в промышленности, а также выясним в каких отраслях промышленности его применяют.
Водород находит широкое применение в технике и лабораторных исследованиях. Мировое промышленное производство водорода из меряется десятками миллионов тонн в год.
Выбор промышленного способа получения простых веществ зависит от того, в какой форме соответствующий элемент находится в природе. Водород находится в природе преимущественно в соединениях с атомами других элементов. Поэтому для его получения необходимо использовать химические методы. Эти же методы применяют для получения водорода и в лабораторной практике.
Получение водорода в лаборатории
В лабораториях водород получают уже известным вам способом, действуя кислотами на металлы: железо, цинк и др. Поместим на дно пробирки три гранулы цинка и прильем небольшой объем соляной кислоты. Там, где кислота соприкасается с цинком (на поверхности гранул), появляются пузырьки бесцветного газа, которые быстро поднимаются к поверхности раствора:
Атомы цинка замещают атомы водорода в молекулах кислоты, в результате чего образуется простое вещество водород Н2, пузырьки которого выделяются из раствора. Для получения водорода таким способом можно использовать не только хлороводородную кислоту и цинк, но и некоторые другие кислоты и металлы.
Соберем водород методом вытеснения воздуха, располагая пробирку вверх дном (объясните почему), или методом вытеснения воды и проверим его на чистоту. Пробирку с собранным водородом наклоняем к пламени спиртовки. Глухой хлопок свидетельствует о том, что водород чистый; «лающий» громкий звук взрыва говорит о загрязненности его примесью воздуха.
В химических лабораториях для получения относительно небольших объемов водорода обычно применяют способ разложения воды с помощью электрического тока:
Из уравнения процесса разложения следует, что из 2 моль воды образуются 2 моль водорода и 1 моль кислорода. Следовательно, и соотношение объемов этих газов также равно:
Получение водорода в промышленности
Очевидно, что при огромных объемах промышленного производства сырьем для получения водорода должны быть легкодоступные и дешевые вещества. Такими веществами являются природный газ (метан СН4) и вода. Запасы природного газа очень велики, а воды — практически неограниченны.
Самый дешевый способ получения водорода — разложение метана при нагревании:
Эту реакцию проводят при температуре около 1000 °С.
В промышленности водород также получают, пропуская водяные пары над раскаленным углем:
Существуют и другие промышленные способы получения водорода.
Применение водорода
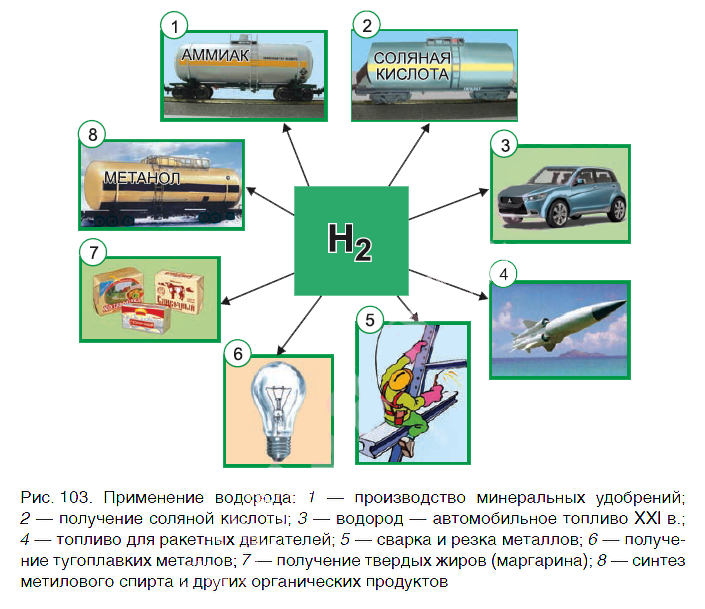
Водород находит широкое практическое применение. Основные области его промышленного использования показаны на рисунке 103.
Значительная часть водорода идет на переработку нефти. Около 25 % производимого водорода расходуется на синтез аммиака NH3. Это один из важнейших продуктов химической промышленности. Производство аммиака и азотных удобрений на его основе осуществляется в нашей стране на ОАО «Гродно Азот». Республика Беларусь поставляет азотные удобрения во многие страны мира.
В большом количестве водород расходуется на получение хлороводородной кислоты. Реакция горения водорода в
кислороде используется в ракетных двигателях, выводящих в космос летательные аппараты. Водород применяют и для получения металлов из оксидов. Таким способом получают тугоплавкие металлы молибден и вольфрам.
В пищевой промышленности водород используют в производстве маргарина из растительных масел. Реакцию горения водорода в кислороде применяют для сварочных работ. Если использовать специальные горелки, то можно повысить температуру пламени до 4000 оС. При такой температуре проводят сварочные работы с самыми тугоплавкими материалами.
В настоящее время в ряде стран, в том числе и в Беларуси, начаты исследования по замене невозобновляемых источников энергии (нефти, газа, угля) на водород. При сгорании водорода в кислороде образуется экологически чистый продукт — вода. А углекислый газ, вызывающий парниковый эффект (потепление окружающей среды), не выделяется.
Предполагают, что с середины XXI в. должно быть начато серийное производство автомобилей на водороде. Широкое применение найдут домашние топливные элементы, работа которых также основана на окислении водорода кислородом.
Краткие выводы урока:
- В лаборатории водород получают действием кислот на металлы.
- В промышленности для получения водорода используют доступное и дешевое сырье — природный газ, воду.
- Водород — это перспективный источник энергии XXI в.
Надеюсь урок 26 «Получение водорода и его применение» был понятным и познавательным. Если у вас возникли вопросы, пишите их в комментарии. Если вопросов нет, то переходите к следующему уроку.
Условие задачи:
Какую работу совершил водород массой 3 г при изобарном нагревании на 100 К?
Задача №5.4.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=3) г, (p=const), (Delta T=100) К, (A-?)
Решение задачи:
Если газ нагревать изобарно, то его объем будет увеличиваться – это можно доказать с помощью закона Гей-Люссака, но мы предлагаем читателю проделать это самостоятельно. Работу газа (A) при изобарном расширении можно найти по формуле:
[A = pleft( {{V_2} – {V_1}} right) = p{V_2} – p{V_1};;;;(1)]
Запишем уравнение Клапейрона-Менделеева для начального и конечного состояния газа:
[left{ begin{gathered}
p{V_1} = frac{m}{M}R{T_1} hfill \
p{V_2} = frac{m}{M}R{T_2} hfill \
end{gathered} right.]
Молярная масса водорода (M) равна 2 г/моль или 0,002 кг/моль.
Если учесть эти два уравнения, то формулу (1) можно записать в виде:
[A = frac{m}{M}R{T_2} – frac{m}{M}R{T_1} = frac{m}{M}Rleft( {{T_2} – {T_1}} right)]
[A = frac{m}{M}RDelta T]
Переведём массу газа (m) в систему СИ:
[3;г = 0,003;кг]
Посчитаем ответ:
[A = frac{{0,003}}{{0,002}} cdot 8,31 cdot 100 = 1246,5;Дж]
Ответ: 1246,5 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.4.20 Один моль газа, имевший начальную температуру 300 К, изобарно расширился
5.4.22 19 м3 воздуха имеют температуру 50 C. Какую работу совершит воздух, расширяясь
5.4.23 В координатах давление-объем график процесса в идеальном одноатомном газе имеет
Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Поэтому принято говорить о двух формах передачи энергии от одних тел к другим: о теплоте и работе.
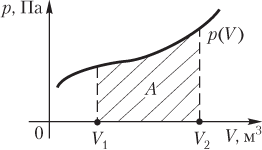
Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p(V). На рис. 6.1 показана произвольная зависимость давления газа p от его объема V (объем газа в начальном состоянии V 1; объем газа в конечном состоянии V 2). Площадь заштрихованной фигуры совпадает с работой, совершенной газом.
Если зависимость p(V) представляет собой прямую линию, то работа численно равна площади прямолинейной трапеции.
В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж).
Работа газа при изобарном процессе (p = const) может быть вычислена по одной из формул:
A = p∆V, или A = νR∆T,
где p — давление газа; ΔV — изменение объема газа при переходе из начального в конечное состояние, ΔV = V 2 − V 1; V 1 — объем газа в начальном состоянии; V 2 — объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); ΔT — соответствующее изменение температуры газа, ΔT = T 2 − T 1; T 1 — абсолютная температура начального состояния; T 2 — абсолютная температура конечного состояния.
Работа газа при изохорном процессе (V = const) не совершается:
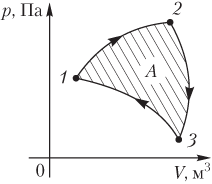
Работа газа при круговом (циклическом) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p(V). На рис. 6.2 показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2, 3 — промежуточные состояния газа.
Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе.
Работа, совершаемая газом за цикл, может быть:
· положительной (прямой цикл);
· отрицательной (обратный цикл).
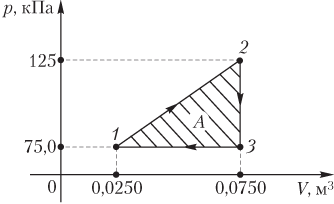
Пример 3. График циклического процесса, происходящего с некоторой массой идеального газа, в координатах p(V) имеет вид прямых, соединяющих точки (0,0250 м 3 ; 75,0 кПа), (0,0750 м 3 ; 125 кПа), (0,0750 м 3 ; 75,0 кПа). Определить абсолютную величину работы, совершаемой газом за цикл.
Решение. На рисунке изображен график циклического процесса в указанных термодинамических координатах p(V).
Величина искомой работы равна площади треугольника, ограниченного прямыми, соединяющими указанные точки:
A=12(125−75,0)⋅103⋅(0,0750−0,0250)=1,25⋅103 Дж=1,25 кДж.
Газ за цикл совершает работу 1,25 кДж.
Пример 4. Газ, состоящий из смеси 2,0 г водорода и 4,2 г гелия, при изобарном нагревании совершил работу 46 кДж. Во сколько раз увеличился объем газа, если его начальная температура была равна 300 К? Молярные массы водорода и гелия равны 2,0 и 4,0 г/моль соответственно.
Решение. Запишем формулу для расчета работы смеси газов при изобарном процессе:
где p — давление смеси газов (постоянная величина), p = const; V 1 — объем смеси газов в начальном состоянии; V 2 — объем смеси газов в конечном состоянии.
Давление смеси газов определяется законом Дальтона:
где p 1 — парциальное давление водорода; p 2 — парциальное давление гелия.
Давления указанных газов в смеси определяются следующими выражениями:
· парциальное давление водорода
где m 1 — масса водорода; M 1 — молярная масса водорода; T 1 — температура смеси газов в начальном состоянии; V 1 — объем смеси газов в начальном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);
· парциальное давление гелия
где m 2 — масса гелия; M 2 — молярная масса гелия.
Подстановка закона Дальтона и явного вида выражений для парциальных давлений водорода и гелия в формулу для работы, совершаемой смесью указанных газов, дает
Преобразование данного уравнения к виду
позволяет выразить искомое отношение объемов
Следовательно, при совершении указанной работы объем смеси увеличился в 10 раз.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Условие задачи:
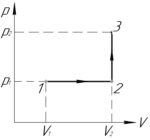
Задача №5.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(V_1=2) л, (V_2=3) л, (p_1=400) кПа, (p_2=600) кПа, (A-?)
Решение задачи:
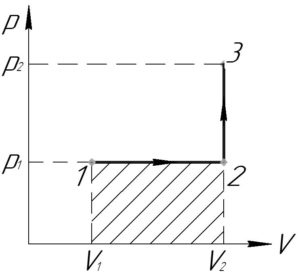
Процесс 1-2 — изобарный, поэтому работу газа (A_<1 — 2>) в этом процессе следует искать по такой формуле (численно работа равна площади фигуры под графиком процесса, на схеме к решению — заштриховано):
Процесс 2-3 — изохорный, работа газа (A_<2 — 3>) в этом процессе равна нулю, так как газ не изменяет своего объема (площадь фигуры под графиком этого процесса в координатах p-V также равна нулю).
В итоге формула (1) примет такой вид:
Переведём объемы газа (V_1) и (V_2) в систему СИ:
Ответ: 400 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода.
Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода. Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Поясните,почему умножение идет 2х10^5 ,когда газ совершает работу от 1 до 2, вроде должно быть 1х10^5,а по ответу получается от 0 до 2.
На участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется. Вся работа совершается на участке 2-3. Общее правило следующее, если процесс изображен на диаграмме , то работа равна площади под графиком со знаком плюс, если объем увеличивается, и со знаком минус, если уменьшается. Для тепловой машины, работающей по циклу, полезная работа равна площади ограниченной этим циклом, это укладывается в ранее озвученное правило. Когда мы идем по «верхней» части цикла, работа идет в +, потом возвращаемся по «нижней» в исходную точку, работа теперь идет в -, в результате остается только кусок внутри.
Алексей, вот Вы сказали, что «на участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется.»
а на участке 2-3 ведь не меняется давление.Так почему работа там совершается? Разве не A=pV ?
Не, не так. Давайте разбираться.
Будем выводить формулу, по которой можно посчитать работу совершенную газом. Когда газ работает? Когда он что-то перемешает. Для этого должен как-то меняться его объем. Например, газ расширяется и толкает поршень вверх, а с ним и какой-то груз, вот Вам и работа. То есть без изменения объема нет работы.
Чтобы вывести формулу, рассмотрим модельную задачу. Рассмотрим цилиндрический сосуд с газом. Пусть сосуд закрыт подвижным поршнем площади . Давление газа равно
. Определим, какую работу совершит газ, когда поршень сдвинется на малое расстояние
. Так как это работа на малом перемещении, то назовем ее элементарной работой и обозначим через
. Работа газа равна произведению силы, с которой он давит на поршень, на перемещение поршня (газ давит нормально, поэтому косинуса не возникает):
. Но сила, с которой газ давит на поршень связана с давлением газа соотношением:
. Если перемещение поршня мало, то можно считать, что давление газа не изменяется сильно и что оно остается постоянным. Тогда:
. Но
— это как раз изменение объема газа
. Окончательно имеем:
.
Получив эту формулу, можно забыть о том, как она выводилась (про сосуд и поршень), она оказывается верной для любого малого изменения объема.
Теперь, чтобы найти работу на конечном изменении объема нужно просуммировать работы по малым изменения, в математике это делается при помощи интеграла: Если внимательно приглядеться, то тут можно как раз увидеть площадь под линией процесса на диаграмме
. Вот почему говорят, что для поиска работы надо искать площадь под графиком на этой диаграмме.
Для частных случаев формула приобретает вид:
1) при изобарном процессе давление выносится за знак интеграла и получаем:
2) при изохорном объем не изменяется, поэтому пределы интегрирования совпадают, интеграл равен нулю, работа равна нулю.
3) при изотермическом процессе, давление уже изменяется с объемом, поэтому надо добавить в рассмотрение уравнение Клапейрона-Менделеева: . Следовательно,
. А значит работа при изотермическом процессе равна:
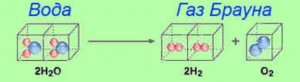
Начнем с того, что все расчеты и цифры приведены для нормальных условий, то есть для среднего давления и комнатной температуры. Мы не будем утомлять Вас сложными формулами, а приведем лишь полезные цифры и информацию, которые помогут на практике.
При расщеплении воды может вырабатываться как отдельно кислород и водород, так и их смесь, называемая газом Брауна или гремучим газом (в народе и на СЕ слэнге «гремучка»). В любом случае топливом является только водород и именно его нужно считать и учитывать.
Основным параметром любого топлива, в том числе и водорода, является его теплотворная способность или удельная теплота сгорания топлива, которые показывают сколько джоулей тепловой энергии будет выделено при сгорании определенного веса или объема вещества. Так как водород — это газ, то нам для расчетов будет удобнее использовать количество Джоулей, выделяемых при сжигании одного литра водорода. То есть Дж/л. Из справочников мы возьмем минимальное усредненное значение, которое равно 10 800 кДж/м3, что в нашем случае составляет 10800 Дж/л. Теперь нам придется вспомнить, каким образом эти цифры можно сопоставить с привычными нам при расчете энергии. За основу давайте возьмем электричество и соответственно его единицы измерения киловатт часы. Тут все просто, 1 ватт мощности это один Джоуль выделяемый за секунду. Отсюда мы без труда выводим следующие цифры, которые пригодятся всем практикам в дальнейшем
— 1 киловатт час электроэнергии это 1 Джоуль * 1000 * 3600 = 3,6 Мега Джоуля или 3,6МДж.
— 1 литр водорода при сжигании выделяет в пересчете на электроэнергию 0,003кВт*часа = 3Ватт часа энергии.
— При КПД приблизительно равном 100%, установка потребляющая мощность 1кВт должна вырабатывать 333,(3) литра водорода в час.
— При КПД приблизительно равном 100% установка потребляющая мощность 1кВт, должна вырабатывать 5,(5) литра водорода в минуту.
Дальше все просто! Имея эти цифры мы без труда можем рассчитать КПД любой установки.
Возьмем для примера классические, продаваемые ныне водородные сварки, которые при потреблении 1,8кВт часа электроэнергии, вырабатывают около 6 литров водорода в минуту. Отсюда следует, что работают они с КПД приблизительно равным 60%. Считается это так: мы знаем, что однокиловаттная установка вырабатывает 5,(5) литра водорода в минуту, а у нас потребление 1,8кВт, значит нам нужно 5,(5) умножить на 1.8, получаем 10. То есть мы выяснили, что для работы со стопроцентным КПД данная установка должна вырабатывать 10 литров водорода, а нам известно со слов производителя, что вырабатывает она максимум 6, значит нам остается только 6 разделить на 10 и умножить на 100%, отсюда и получена цифра в 60%.
С водородом мы разобрались и по-моему тут все просто, теперь давайте сделаем то же самое для газа Брауна или «гремучки». Так как газ Брауна содержит в себе две части водорода и одну часть кислорода, а топливом является только водород, то все наши полученные выше цифры необходимо умножить приблизительно на две третьих (2/3). Отсюда мы получаем:
— 1 литр газа Брауна при сжигании выделяет в пересчете на электроэнергию 0,002кВт*часа = 2Ватт часа энергии.
— При КПД приблизительно равном 100%, установка потребляющая мощность в 1кВт должна вырабатывать 500 литров газа Брауна в час.
— При КПД приблизительно равном 100% установка потребляющая мощность в 1кВт, должна вырабатывать 8,(3) литра газа Брауна в минуту.
Вот и все основные цифры, которые могут понадобиться для приблизительной теоретической оценки вырабатываемого электролизерами газа и его эффективности. Следует также еще раз особо отметить, что цифры даны минимальные и относятся они только к сугубо теоретическим аспектам, которые далеко не всегда подтверждаются на практике. . К ним смело можно прибавить 10%.
Рассмотрим один из недавних примеров, достоверность которого нам известна доподлинно, равно как и все приведенные ниже цифры.
Мы уже публиковали по нему несколько статей и видео, а по последним опытам можем только лишь добавить, что в настоящий момент прототип генератора при потребление от сети тока в девять ампер, вырабатывает в минуту 24 литра газа Брауна. По расчетам получается следующее:
9*220=1,98кВт, таким образом получается, что при 100% КПД выработка газа должна быть 1,98*8,3=16 литров в минуту, а при реальных 24-х литрах установка по всем теоретическим расчетам работает с КПД превышающим 150%, что само по себе не может не радовать. Но все дело в том, что на практике этот КПД еще в несколько раз выше. Рассмотрим еще один вполне конкретный пример.
Были проведены опыты с обычным четырехкиловаттным бензиновым генератором, который был переделан на газ Брауна и был запущен в режиме самозапитки.
На практике были получены следующие основные цифры: на собственную работу, то есть на выработку четырех киловатт энергии генератор тратил только два киловатта вырабатываемой мощности, отдавая оставшиеся два киловатта в полезную нагрузку. При этом электролизер был менее эффективной модели, который от двух киловатт вырабатывал не более 18 литров водорода в минуту и даже меньше, но при этом двигатель все равно устойчиво работал, отдавая в нагрузку два киловатта полезной мощности. Если вспомнить, что КПД классического двигателя внутреннего сгорания не превышает 30%, то есть всего 30% из подаваемого газа идет на генерацию электроэнергии, то получаются совершенно другие цифры.
На практике получается, что даже этот, далеко не самый эффективный на данный момент электролизер, работает с КПД превышающим 600%!
На вопрос «откуда дровишки», то есть откуда же берется этот самый прирост энергии, мы ответить пока не можем и оставляем его физикам-теоретикам. Мы можем лишь еще раз подтвердить, что все описанное выше имеет место быть в том виде, в котором мы и описали и каждый желающий сможет в этом убедиться. Добавим лишь, что мы не посягаем на правильность первого и второго начала термодинамики и на закон сохранения энергии, находя их вполне адекватными и рабочими, что в нашем случае подразумевает только лишь наличие и использование в данной установке дополнительно какого-либо другого вида энергии, который тем не менее пока не вписывается в рамки классической теоретической физики.
На правах рекламы, продолжаем знакомить Вас с интересными сайтами.
На этом сайте продается Тренинг уверенности в себе со скидкой. К сожалению мы сами не проходили данный курс, по этому ничего о нем сказать не можем, но выглядит красиво.
| 🎓 Заказ №: 22193 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Химия |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 153 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Вычислить работу расширения, если 100 г водорода в изотермическом процессе, при 50 °С расширяются от объема 0,04 м3 до 0,2 м3 .
Решение: Принимаем водород в данном случае за идеальный газ При изотермическом расширении идеальный газ полностью преобразует получаемое тепло в совершаемую работу. 1 2 ln V V А vRT где: v количество вещества, моль; R универсальная газовая постоянная, 8,314 Дж/(моль∙K); T абсолютная температура, K; V2 конечный объем, м3 ; V1 конечный объем, м3 . Количество вещества равно отношению массы вещества к молярной массе вещества M m v
Готовые задачи по химии которые сегодня купили:
- Приведите метод Кьельдаля и видоизмененный вариант Кьельдаля для аминокислот и их производных.
- Составить примерный план анализа при подозрении на отравление алкалоидами – производными изохинолина (папаверин).
- Рассчитать константу гидролиза и степень гидролиза (%) в растворе ацетата натрия с молярной концентрацией 0,01 моль/дм3 .
- Предложите методы количественного определения ингредиентов лекарственной смеси: Фурацилина 0,02 Натрия хлорида 0,8 Дайте им обоснование, напишите химизм реакций, выведите молярные массы эквивалентов.
- Определить, выпадет ли осадок при сливании равных объемов растворов хлорида бария с С(BaCl2) = 0,0001 моль/л и серной кислоты с С(H2SO4) = 0,00005 моль/л.
- При фотометрическом определении титана с хромотроповой кислотой в растворе, содержащем 11,496 мкг титана в 10,00 см3 , в кювете толщиной 2 см была получена оптическая плотность равная 0,245.
- Напишите формулу ЛС, исходя из химического названия: l-1-(3,4- диоксифенил)-2-метиламиноэтанола гидротартрат.
- Какой объем нитрата серебра с ТAgNO3 = 0,005040 г/см3 пойдет на титрование 20,00 см3 раствора, полученного растворением 0,1000 г хлорида калия в мерной колбе вместимостью 250,00 см3 ?
- Как изменится скорость реакции 2NO O2 2NO2 , если уменьшить объем реакционного сосуда в 3 раза?
- Рассчитайте интервал объемов 0,1 М раствора натрия нитрита (Kп = 0,9984), который будет обеспечивать качество анестезина (М.м. 165,19) по количественному содержанию с учетом требования ФС 42-3024-94, с.87 (анестезина должно быть не менее 99,5 % в пересчете на сухое вещество), если навеска 0,2000 г.