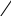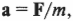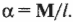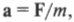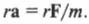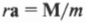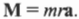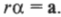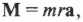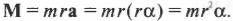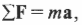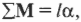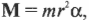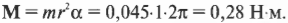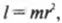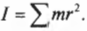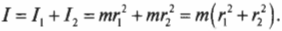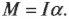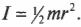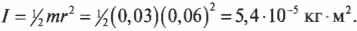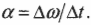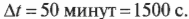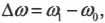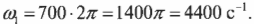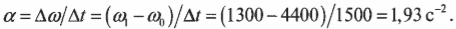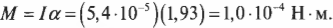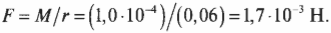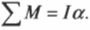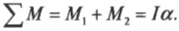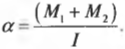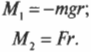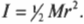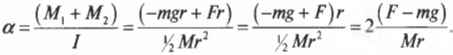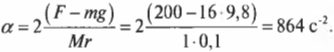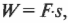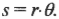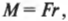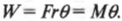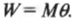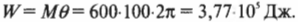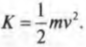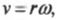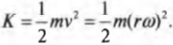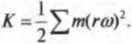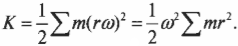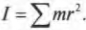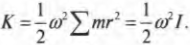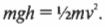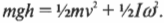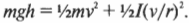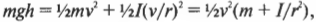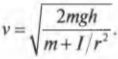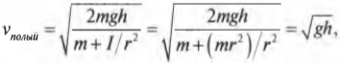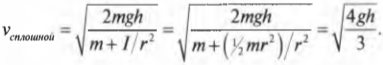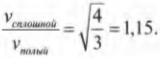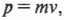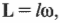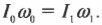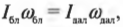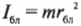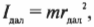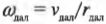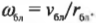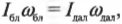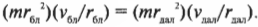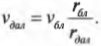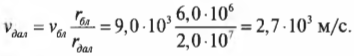Как найти работу вращения

1. Механическая работа при вращательном движении твердого тела

Механическую
работу при вращении твердого тела вокруг
неподвижной оси можно вычислить,
воспользовавшись тем фактом, что она
идет на приращение кинетической энергии
материальных точек этого тела, то есть

Используя
(4.21), легко найти (
),
что

.

Учтя
теперь, что

,
а

—
элементарный угол поворота тела вокруг
оси Z, придем к выражению
для механической работы

(4.23)

При
повороте тела на конечный угол 
вокруг неподвижной оси для вычисления
работы необходимо проинтегрировать
выражение (4.23)

(4.24)

Контрольные
вопросы.

4.7.
Покажите, что если воспользоваться
общим выражением для механической
работы

,
то при вращении тела вокруг неподвижной
оси тоже получается формула (4.23).

4.8. Изменится
ли и как выражение для работы (4.23), если
тело под действием внешних сил совершает
плоское движение?

4.6. Сравнение описаний движения материальной точки и вращения твердого тела

Здесь в виде
таблицы показана аналогия между видом
основных физических величин и соотношений,
описывающих механику поступательного
и вращательного движений твердого тела:

КИНЕМАТИКА
Поступательное движение	Вращательное движение
— элементарное перемещение	— элементарный угол поворота
— линейная скорость	— угловая скорость
— линейное ускорение	— угловое ускорение
Уравнения равнопеременного движения:	Уравнения равнопеременного вращения вокруг неподвижной оси

ДИНАМИКА
— сила	— момент силы
— масса	— момент инерции относительно данной оси
— импульс	— момент импульса
— основное уравнение динамики поступательного движения	— основное уравнение динамики вращательного движения
, если — закон сохране-ния импульса	, если — закон сохранения момента импульса
— кинетическая энергия	— кинетическая энергия при вращении вокруг неподвижной оси
— механическая работа	— механическая работа при вращении твердого тела

Выводы: Физические
законы и соотношения, описывающие
поступательное и вращательное движения
твердого тела, имеют совершенно
аналогичную форму и могут быть получены
друг из друга простой заменой линейных
физических величин на соответствующие
угловые или наоборот.

1. Применение основных законов динамики твердого тела при решении конкретных задач

При решении
конкретных задач, связанных с описанием
движения твердого тела, следует помнить,
что твердое тело в механике представляет
собой частный случай системы материальных
точек, имеющих в процессе рассматриваемого
движения неизменное друг относительно
друга взаимное расположение. Как уже
указывалось (3.7) и (3.3), в этом случае
справедливы основные уравнения динамики

(4.25)

и

.
(4.26)

Из этих
уравнений непосредственно видно, что
характер движения твердого тела полностью
определяется действующими на него
внешними силами

и моментами этих сил

.

Для практического
применения основных уравнений (4.2) и
(4.26) полезно следовать рекомендациям,
упрощающим решение конкретных задач:

— Сделать
схематический чертеж, на котором указать
все внешние силы, действующие на
рассматриваемое тело. При этом силы
следует изображать в тех точках тела,
на которые эти силы действуют.

—
Выбрать инерциальную систему отсчета,
связанную с какой-либо неподвижной или
движущейся равномерно и прямолинейно
точкой, относительно которой определяются
моменты внешних сил. Если тело имеет
неподвижную ось вращения, то полезно
эту точку выбрать на неподвижной оси,
а ось 0Z декартовой системы
координат направить вдоль оси вращения.
В случае плоского движения твердого
тела ось 0Z рекомендуется
направить перпендикулярно плоскости,
в которой лежит траектория какой-либо
точки тела.

— Точку приложения конкретной силы можно
перемещать вдоль линии действия силы,
так как при этом момент этой силы не
изменяется. Это полезно делать при
необходимости определения равнодействующей
внешних сил.

—
Записать уравнения (4.25) и (4.26) в проекциях
на оси координат выбранной системы
отсчета и, с использованием уравнений
связи (например,

)
и дополнительных условий задачи, решить
полученную систему уравнений относительно
искомой величины.

y







0

z

ц.м.

x

Рис. 4.6

Для примера подробно
исследуем свободное вращение жесткого
однородного стержня массой

и длиной

в вертикальной плоскости относительно
горизонтальной оси, проходящей через
один из его концов (рис. 4.6). Трением в
оси пренебрегаем. Выберем оси координат,
как указано на рис. 4.6 (ось Z
направлена из-за чертежа вдоль оси
вращения стержня). При свободном вращении
на стержень действуют две силы: сила
тяжести

и реакция оси вращения

.
Поэтому уравнения динамики (4.25) и (4.26)
примут вид

,

,

где

и

—
моменты сил

и

соответственно. Запишем эти уравнения
в проекциях на выбранные оси координат

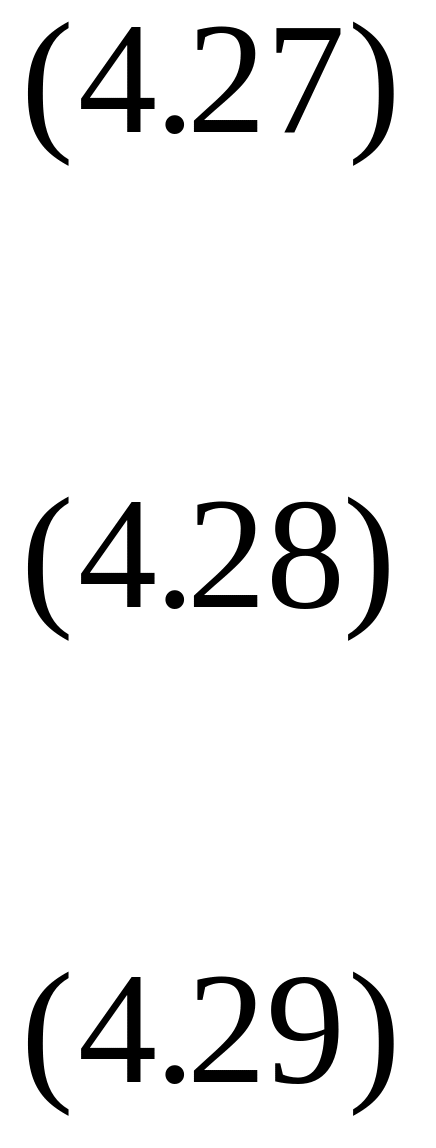
где угол

отсчитывается от оси

.

В уравнении
(4.29) учтено, что

относительно оси вращения равен нулю.
Исследование удобнее и проще всего
проводить, если перейти в уравнениях
(4.27)-(4.29) от переменной

к переменной

.
Заметим, что в этом случае

,
кроме этого, учтем, что

относительно оси вращения, согласно
(4.13). Теперь уравнения (4.27)-(4.29) примут
вид:

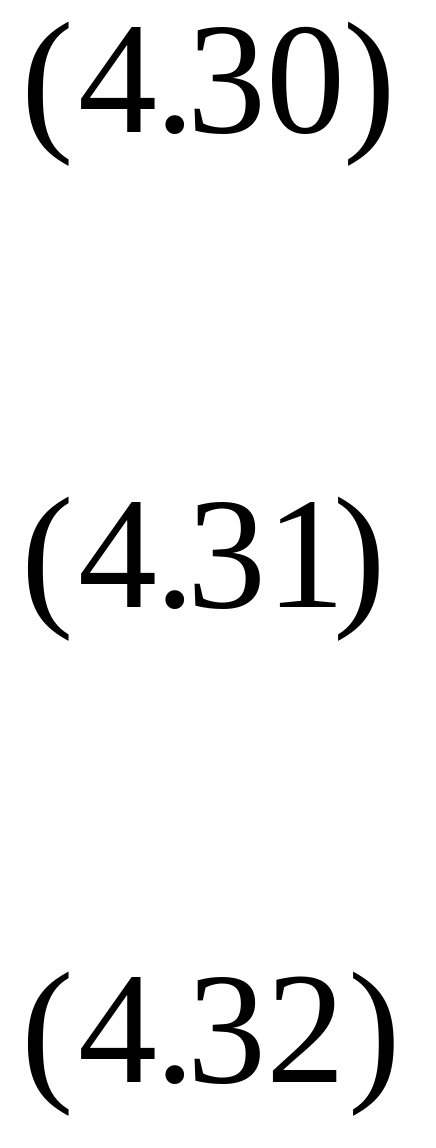
Легко заметить,
что последнее равенство (4.32) эквивалентно
условию

что проверяется
прямым дифференцированием. Равенство
нулю производной означает, что сумма в
скобках при вращении стержня остается
постоянной, то есть

Значение
константы определим, положив, например,

при

,
что соответствует началу вращения
стержня из вертикального положения без
толчка. В этом случае

,
поэтому

,
при заданных начальных условиях

.
Поэтому значение угловой скорости
стержня в любом его положении определяется
равенством

.
(4.33)

Используя
связь (1.31), найдем теперь значения модуля
скорости центра масс стержня

,
(4.34)

а затем и
проекций

на оси координат

(4.35)

(4.36)

Уравнения
(4.30) и (4.31) позволяют определить проекции
силы

,
для этого необходимо, соответственно,
использовать (4.35) и (4.36):

,
(4.37)

.
(4.38)

Интересно
отметить, что при вращении сила

,
вообще говоря, не направлена вдоль
стержня, а составляет с вертикалью (с
осью 0Y) угол

.
(3.39)

Модуль
силы

равен

(4.40)

и нигде в нуль
не обращается.

Выводы: Свободное
вращение стержня в вертикальной плоскости
является неравномерным. Зависимости
угловой скорости вращения, скорости
его центра масс, а также реакции оси от
положения стержня определяются формулами
(4.33)-(4.40).

Контрольные
вопросы.

4.9. Покажите,
что равенство (4.33) является следствием
из закона сохранения механической
энергии стержня.

4.10.
Определите, в каких положениях стержня
(
-?)
реакция его оси направлена а) горизонтально;
б) вертикально; в) вдоль стержня?

1. 
   

   

   

   
   
   

   
   
   
   
   
   
   
   

   C

   

   

   

   

   

   

   

   
   
   

   0

   

   y

   

   x

   Рис. 4.7 Рис. 4.8

   П
   

   

   
   

   z

   онятие о прецессии

Рассмотрим
здесь качественно характер движения
симметричного твердого тела, имеющего
одну неподвижную точку 0 (рис. 4.7), которая
лежит на оси симметрии тела

.
В динамике вращательного движения такое
тело называется гироскопом
или симметричным волчком. Примером
такого тела является обыкновенный
детский волчок (юла). Поставим волчок
на горизонтальную опору и приведем его
в быстрое вращение относительно оси
симметрии

,
в результате волчок приобретет момент
импульса

,
направленный вдоль оси

.

Дальнейшее
движение волчка будет определяться
результирующим моментом сил, действующих
на волчок относительно неподвижной
точки

,
который равен

и направлен
перпендикулярно плоскости

(рис. 4.8). Заметим, что момент силы реакции
опоры относительно точки

равен нулю.

Из-за
действия момента силы тяжести

,
в соответствии с уравнением моментов
(3.52), за время

момент импульса волчка

получит приращение

,
равное

.

Отметим,
что

,
а поэтому приращение

направлено перпендикулярно плоскости

.
Таким образом, ось волчка

за время

повернется в направлении

на некоторый угол

.
Поскольку взаимная ориентация векторов

,

и плоскости

в любой момент времени остается
неизменной, то ось вращения волчка

будет поворачиваться относительно
вертикали

,
описывая конусообразную поверхность.

Подобный
характер движения будет наблюдаться,
когда симметричное твердое тело, имеющее
одну неподвижную точку и вращающееся
вокруг оси симметрии, подвержено действию
постоянного по величине внешнего момента
силы. При этом его ось вращения сама
поворачивается относительно неподвижной
оси — такое вращение называется прецессией.

Особое
распространение в технике получили так
называемые уравновешенные гироскопы,
когда неподвижной точкой при вращении
гироскопа является его центр инерции,
а собственная ось вращения гироскопа
может свободно поворачиваться в любом
из трех взаимно перпендикулярных
направлений. Таким образом, собственная
ось вращения гироскопа является
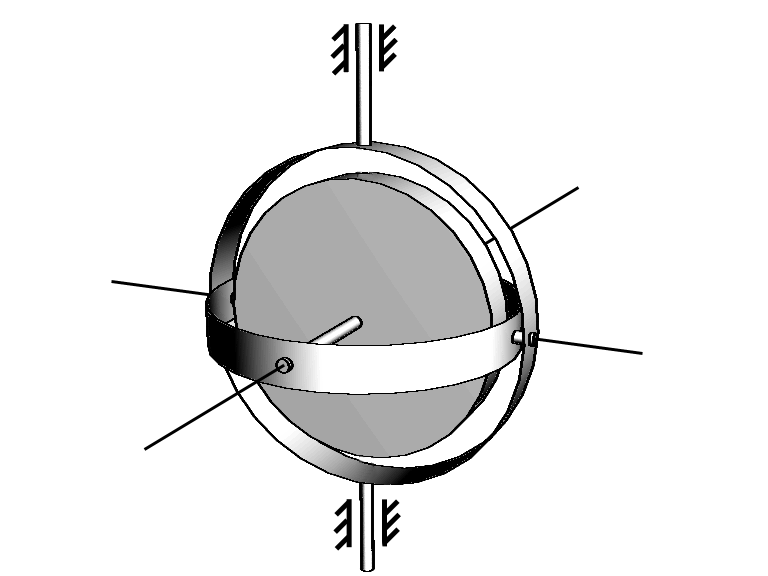
свободной. Это достигается с помощью
так называемого карданова подвеса (рис.
4.9), в котором оси внешнего

и внутреннего

колец и собственная ось гироскопа

пересекаются в одной точке: центре
подвеса. Уравновешенные гироскопы
являются основным элементом автоматического
управления в навигационных приборах
движущихся объектов (самолетов, кораблей,
ракет и т.д.), а также используются в
приборах для измерения угловых и линейных
скоростей. Действие подобных приборов
основано на главном свойстве гироскопа:
при любых поворотах оси внешнего кольца,

0₁

0

0₂

0₂

0₁

0

Рис. 4.9

неподвижной
относительно движущегося объекта
(например, самолета), собственная ось
вращения гироскопа

не изменяет своей ориентации в
пространстве. Это свойство непосредственно
следует из закона сохранения момента
импульса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Работа при вращательном движении. Момент силы

Рассмотрим работу, совершаемую при вращении материальной точки по окружности под действием проекции действующей силы на перемещение (тангенциальной составляющей силы). В соответствии с (3.1) и рис. 4.4, перейдя от параметров поступательного движения к параметрам вращательного движения (dS = R dcp)

Здесь введено понятие момента силы относительно оси вращения OOi как произведение силы F_s на плечо силы R:

Как видно из соотношения (4.8), момент силы во вращательном движении является аналогом силы в поступательном движении, поскольку оба параметра при умножении на аналоги dcp и dS дают работу. Очевидно, момент силы тоже должен задаваться векторно, причем относительно точки О его определение дается через векторное произведение и имеет вид

Окончательно: работа при вращательном движении равна скалярному произведению момента силы на угловое перемещение:

Кинетическая энергия при вращательном движении. Момент инерции

Рассмотрим абсолютно твердое тело, вращающееся относительно неподвижной оси. Мысленно разобьем это тело на бесконечно малые кусочки с бесконечно малыми размерами и массами mi, m2, Шз . находящиеся на расстоянии R_b R₂, R3 . от оси. Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его малых частей

где У— момент инерции твердого тела, относительно данной оси OOj.

Из сопоставления формул кинетической энергии поступательного и вращательного движений видно, что момент инерции во вращательном движении является аналогом массы в поступательном движении. Формула (4.12) удобна для расчета момента инерции систем, состоящих из отдельных материальных точек. Для расчета момента инерции сплошных тел, воспользовавшись определением интеграла, можно преобразовать (4.12) к виду

Несложно заметить, что момент инерции зависит от выбора оси и меняется при ее параллельном переносе и повороте. Приведем значения моментов инерции для некоторых однородных тел.

Из (4.12) видно, что момент инерции материальной точки равен

где т — масса точки;

R — расстояние до оси вращения.

Несложно вычислить момент инерции и для полого тонкостенного цилиндра (или частного случая цилиндра с малой высотой — тонкого кольца) радиуса R относительно оси симметрии. Расстояние до оси вращения всех точек для такого тела одинаково, равно радиусу и может быть вынесено из-под знака суммы (4.12):

Сплошной цилиндр (или частный случай цилиндра с малой высотой — диск) радиуса R для расчета момента инерции относительно оси симметрии требует вычисления интеграла (4.13). Масса в этом случае в среднем сосредоточена несколько ближе, чем в случае полого цилиндра, и формула будет похожа на (4.15), но в ней появится коэффициент меньше единицы. Найдем этот коэффициент.

Пусть сплошной цилиндр имеет плотность р и высоту h. Разобьем его на

полые цилиндры (тонкие цилиндрические поверхности) толщиной dr (рис. 4.5) показывает проекцию, перпендикулярную оси симметрии). Объем такого полого цилиндра радиуса г равен площади поверхности, умноженной на толщину: масса: а момент

инерции в соответствии с (4.15): Полный момент

инерции сплошного цилиндра получается интегрированием(суммированием) моментов инерции полых цилиндров:

. С учетом того, что масса сплошного цилиндра связана с

плотностью формулой т = 7iR 2 hp имеем окончательно момент инерции сплошного цилиндра:

Аналогично ищется момент инерции тонкого стержня длины L и массы т, если ось вращения перпендикулярна стержню и проходит через его середину. Разобьем такой стержень в соответствии с рис. 4.6

на кусочки толщиной dl. Масса такого кусочка равна dm=m dl/L, а момент инерции в соответствии с Пол

ный момент инерции тонкого стержня получается интегрированием (суммированием) моментов инерции кусочков:

Взятие элементарного интеграла дает момент инерции тонкого стержня длины L и массы т:

Несколько сложней берется интеграл при поиске момента инерции однородного шара радиуса R и массы т относительно оси симметрии. Пусть сплошной шар имеет плотность р. Разобьем его в соответствии с рис. 4.7 на полые тонкие цилиндры толщиной dr, ось симметрии которых совпадает с осью вращения шара. Объем такого полого цилиндра радиуса г равен площади поверхности, умноженной на толщину, , где высота цилиндра h

найдена с использованием теоремы Пифагора: Тогда несложно найти массу полого цилиндра , а также

момент инерции в соответствии с (4.15):

Полный момент инерции сплошного шара получается интегрированием (суммированием) моментов инерции полых цилиндров:

С учетомтого, что масса сплошного шара связана с плотностью формулой , имеем окончательно момент инерции относительно оси симметрии однородного шара радиуса R массы т:

Работа и мощность при вращательном движении

Работа. Вращательное движение обеспечивается приложенным к телу вращательным моментом относительно оси, который создаётся парой сил РР (рис. 38) и определяется по формуле

Рис. 38 Вращательный момент

При повороте тела на угол ср, работа А совершается силой Р, перемещённой из точки С в точку Ci. Полное перемещение точки приложения силы S равно длине дуги радиусом R_y то есть

Поскольку сила Р всегда направлена по касательной к перемещению 5, то совершаемая работа будет

Сила Р приложенная в неподвижной точке О работы не совершает.

Учитывая, что , окончательно находим:

Работа постоянной силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота.

Мощность. Если работа совершается силой, приложенной к вращающемуся телу, и притом равномерно, то мощность в этом случае определяют по формуле

Таким образом, мощность силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угловую скорость.

Подставив в выражение мощности значение угловой скорости, получим

Если крутящий момент выражается в Н м, а частота вращения в оборотах в минуту, то мощность выражается в ваттах (Вт).

Вращательное движение тела в физике — виды, формулы и определения с примерами

Содержание:

Вращательное движение тела:

До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).

Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.

Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.

Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги

где — скорость движения тела по окружности; — пройденный телом путь (длина дуги); — время движения тела.

Направление скорости проще всего определить на опыте.

Опыт:

К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).

Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.

Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22).

Опыт:

Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.

Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.

Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.

Период обращения — это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.

Обозначается период обращения большой латинской буквой Т.

Если за время материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:

Единицей периода обращения в СИ является одна секунда (1 с).

Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.

Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности

Обозначается частота обращения малой латинской буквой .

* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой (ню).

Если за время материальная точка совершила N оборотов, то, чтобы определить частоту обращения , нужно N поделить на , т. е.:
а так как = ТN , то .
Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.

Единицей частоты обращения в СИ является единица, разделённая на секунду . это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду , часто применяют также единицу один оборот в минуту .

Движение точки по окружности

Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.

Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.

Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время переходит из точки А в точку В. При этом отрезок OA поворачивается на угол — угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:

где (греческая буква «омега») — угловая скорость; (греческая буква «фи») — угловое перемещение.

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки — длина дуги окружности АВ — равна длине радиуса R.

Единицей угловой скорости является радиан в секунду (рад/с).

1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.

При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).

Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.

Период вращения (Т) — это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:

где t — время вращения, N — количество выполненных оборотов.

Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):

где N — количество совершенных оборотов за время t .

Частота вращения измеряется в оборотах за секунду (об/с).

Частота вращения определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.

Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой («пи»).

Таким образом, длина окружности

За один оборот материальная точка осуществляет угловое перемещение 2 рад.

Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь то линейная скорость равномерного движения точки по окружности или

Вращение твердого тела

Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.

Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.

В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?

Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.

Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния — чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение всех точек одинаково. Следовательно, и угловая скорость для всех точек данного тела также будет одинаковой.

Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т — время одного полного вращения; вращательная частота (частота вращения) — количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.

Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.

Динамика вращательного движения

При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.

Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:

По третьему закону Ньютона:

и при вращении появляется также центробежная сила.
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.

На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом . В точке 1, из-за того что центробежная сила направлена противоположно силе тяжести , вес тела уменьшается:

В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:

Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения.
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.

Пример

При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки . Скорость тела в точке равна 30 м/с.
Дано:

Чтобы тело не упало из точки должно выполняться следующее условие:

Ответ: 90 м.

Кинематика вращательного движения

При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.

Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.

Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.

Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота (рис. 25)

радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:

По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению

Скорость с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).

Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения

Модуль угловой скорости — это отношение угла поворота к промежутку времени за который этот поворот произошел:

Угловая скорость со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).

Единица угловой скорости в СИ — радиан в секунду

При движении по окружности с постоянной по модулю скоростью v угловая скорость является величиной постоянной и ее модуль равен отношению угла поворота к промежутку времени за который этот поворот произошел:

Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:

Единица частоты вращения в СИ — секунда в минус первой степени Время совершения одного оборота называется периодом вращения Т.

В СИ период измеряется в секундах (1с).

При совершении полного оборота период определяется по формуле

Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле

Проекции скорости (см. рис. 25) с течением времени изменяются по закону

Модуль угловой скорости определяется соотношением

Следовательно, соотношение между модулями линейной и угловой скорости имеет вид

Поскольку (докажите самостоятельно), где — угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид

При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным или нормальным Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости с течением (см. рис. 26). Его модуль определяется формулой

Нормальное ускорение в любой момент времени перпендикулярно скорости

Как и при прямолинейном равноускоренном движении, ускорение называемое тангенциальным (касательным), совпадает с направлением скорости или направлено противоположно ей и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение можно представить в виде векторной суммы нормального ускорения и тангенциального ускорения направленного по касательной к окружности в данной точке (рис. 28):

Полное ускорение всегда направлено в сторону вогнутости траектории (см. рис. 28).

Модуль полного ускорения находится по теореме Пифагора:

где — нормальное ускорение, с которым точка двигалась бы по дуге
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Равномерное движение материальной точки по окружности
• Колебательное движение
• Физический и математический маятники
• Пружинные и математические маятники
• Поступательное движение
• Равномерное и неравномерное движение
• Равномерное движение
• Неравномерное движение

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

В этой главе…

• Переходим от динамики поступательного движения к динамике вращательного движения
• Вычисляем момент инерции
• Определяем работу вращательного движения
• Находим связь между работой и изменением кинетической энергии
• Изучаем закон сохранения момента импульса

Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.

Применяем второй закон Ньютона для вращательного движения

Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:

где ​( mathbf{a} )​ — это вектор ускорения, ( mathbf{F} ) — вектор силы, а ​( m )​ — масса объекта. Подробнее о векторах рассказывается в главе 4. Соблюдается ли этот закон для вращательного движения?

В главе 10 мы уже познакомились характеристиками вращательного движения, которые являются эквивалентами (аналогами) некоторых характеристик поступательного движения. А как будет выглядеть аналог у второго закона Ньютона? Похоже, что во вращательном движении роль ускорения ( mathbf{a} ) играет угловое ускорение ( alpha ), а роль силы ( mathbf{F} ) — момент силы ( mathbf{M} )? Не вдаваясь в подробности, скажем лишь, что это действительно так. А что же с массой? Оказывается, что для этого используется новое понятие — момент инерции ​( l )​. Известно, что второй закон Ньютона для вращательного движения принимает следующий вид:

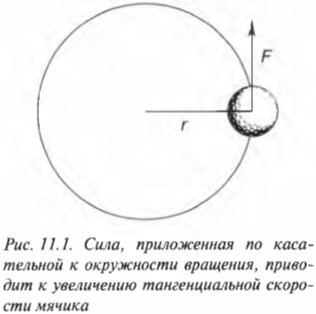
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)

Поскольку:

то, умножая обе части этой формулы на радиус окружности ​( r )​, получим:

Поскольку ​( rmathbf{F}=mathbf{M} )​ то

или

Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ​( r )​. Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)

Преобразуем тангенциальное ускорение в угловое

Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ​( alpha )​ и тангенциальным ускорением ​( mathbf{a} )​. Как нам уже известно из главы 10, они связаны следующим соотношением:

Подставляя это выражение в приведенную выше формулу

получим:

Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ​( l=mr^2 )​, называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.

Пример: вычисляем момент силы для обеспечения углового ускорения

Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:

где ​( mathbf{sum!F} )​ обозначает векторную сумму всех сил, действующих на объект.

Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:

где ( mathbf{sum! M} ) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м².

Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ​( mathbf{sum! M}=lalpha )​, т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.

Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ​( 2pi с^{-2} )​? Подставляя значения в уже известную нам формулу

получим:

Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.

Вычисляем момент инерции протяженного объекта

Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ​( r )​. В таком случае момент инерции имеет знакомый вид:

где ( r ) — это расстояние, на котором сосредоточена вся масса мячика ( m ).

Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:

Например, момент инерции ​( l )​ системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ​( m )​ на расстояниях ​( r_1 )​ и ​( r_2 )​ равен сумме их отдельных моментов инерции ​( l_1=mr_1^2 )​ и ( l_2=mr_2^2 ):

А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.

Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.

Пример: замедление вращения компакт-диска

Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:

Момент инерции диска с радиусом ​( r )​, вращающегося относительно своего центра в плоскости диска, выражается формулой:

Подставляя значения, получим:

Теперь нужно определить угловое ускорение, которое определяется следующей формулой:

Изменение угловой скорости ​( Deltaomega )​ произошло за промежуток времени:

В данном примере изменение угловой скорости:

где ​( omega_1 )​ — конечная, а ( omega_0 ) — начальная угловая скорость компакт-диска.

Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ​( 2pi )​ радиан:

Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит ( 2pi ) радиан:

Подставляя значения в формулу углового ускорения, получим:

Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:

Итак, средний момент равен 10^-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:

Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.

Еще один пример: поднимаем груз

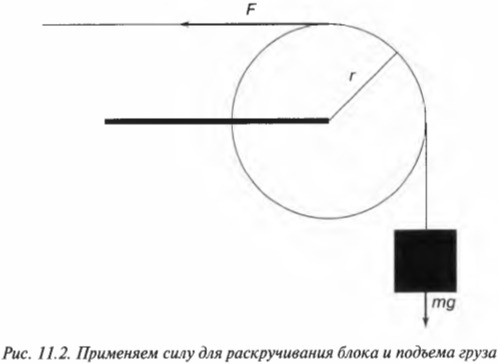
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.

В данном примере нужно вычислить сумму всех моментов сил ​( mathbf{sum! M} )​, которые действуют на веревку:

В данном примере на веревку действует два момента сил: один ​( M_1 )​ со стороны груза весом ​( mg )​, а другой ( M_2 ) — со стороны горизонтальной силы ​( F )​:

Отсюда получаем формулу для углового ускорения:

Эти моменты ​( M_1 )​ и ( M_2 ) имеют одинаковое плечо, равное радиусу блока ​( r )​, поэтому:

Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:

Подставляя выражения для ​( l )​, ​( M_1 )​ и ​( M_2 )​ в формулу для углового ускорения, получим:

Подставляя значения, получим:

 

Вычисляем энергию и работу при вращательном движении

При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.

Работа при вращательном движении

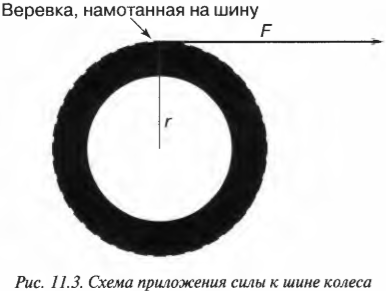
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.

Пусть шина имеет радиус ​( r )​ и для ее вращения используется сила ​( F )​, как показано на рис. 11.3.

Чему равна работа этой силы? Применим знакомую нам формулу:

где ​( s )​ — это перемещение веревки под действием этой силы. В данном примере перемещение ​( s )​ равно произведению радиуса ​( r )​ на угол поворота шины ​( theta )​:

Подставляя это выражение в формулу работы, получим:

Поскольку момент ​( M )​, создаваемой этой силой, равен:

то получаем для работы:

Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.

Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.

Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:

Полный оборот соответствует повороту на угол ​( 2pi )​. Подставляя значения в формулу, получим:

Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.

Изучаем кинетическую энергию вращательного движения

Из главы 8 нам уже известно, что объект массы ​( m )​, движущийся поступательно со скоростью ​( v )​, обладает кинетической энергией:

А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.

При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.

Как известно (см. главу 10), тангенциальная скорость ​( v )​ и угловая скорость ​( omega )​ связаны соотношением:

где ​( r )​ — это радиус окружности вращения.

Подставляя это соотношение в предыдущую формулу, получим:

Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:

Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:

Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:

Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:

Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.

Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости

Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.

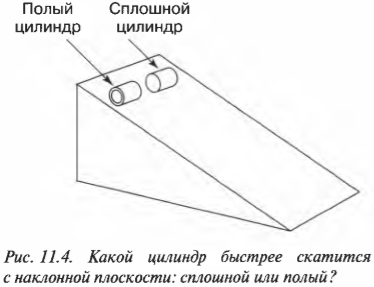
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ​( h )​ скатываются сплошной и полый цилиндры с одинаковой массой ​( m )​. Какой цилиндр достигнет нижнего конца наклонной плоскости?

Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ​( mgh )​ преобразуется в увеличение кинетической энергии только поступательного движения ​( {}^1!/!_2mv^2 )​, т.е.:

Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения ( {}^1!/!_2mv^2 ), а часть — в кинетическую энергию вращательного движения ( {}^1!/!_2Iomega ^2 ). Тогда предыдущее равенство принимает следующий вид:

Сделаем подстановку ​( omega=v/r )​ и получим:

Путем несложных алгебраических преобразований получим:

откуда легко получить выражение для скорости цилиндра:

Для обоих цилиндров все параметры одинаковы, кроме момента инерции ​( I )​. Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ​( mr^2 )​, а сплошной — ​( {}^1!/!_2mr^2 )​.

Итак, для полого цилиндра получим:

а для сплошного цилиндра:

А их отношение равно:

Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.

Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.

Не можем остановиться: момент импульса

Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.

В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:

где ​( m )​ — это масса, a ​( v )​ — скорость материальной точки.

По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):

где ​( l )​ — это момент инерции, а ​( omega )​ — угловая скорость материальной точки.

Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.

Момент импульса в системе СИ измеряется в кг·м²·с^-1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.

Сохраняем момент импульса

Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ​( omega_0 )​ и его моменты инерции в позе с разведенными руками ​( I_0 )​ и в позе с сомкнутыми руками ​( I_1 )​, легко найти конечную угловую скорость ​( omega_1 )​ по формуле:

Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.

Пример закона сохранения момента импульса: вычисляем скорость спутника

Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·10⁶ м от центра Плутона и имеет скорость 9·10³ м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·10⁷ м от центра Плутона?

Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.

Итак, рассмотрим формулу закона сохранения момента импульса:

где ​( I_{бл} )​ — это момент инерции спутника в самой близкой точке, ( I_{дал} ) — это момент инерции спутника в самой далекой точке, ( omega_{бл} ) — угловая скорость спутника в самой близкой точке, а ( omega_{дал} ) — угловая скорость спутника в самой далекой точке.

Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:

и

где ​( r_{бл} )​ — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а ( r_{дал} ) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.

Кроме того:

и

Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса

получим:

Отсюда путем несложных алгебраических преобразований, получим:

Подставляя значения, получим:

Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.