Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)
Формула работа выхода электронов
В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении. Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.
Потенциальная энергия электрона внутри металла постоянна и равна:
Wp = -eφ , где j – потенциал электрического поля внутри металла.
При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.
В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.
Aвых = eφ
Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.
Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми EF . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.
Aвых = eφ’ — EF
где φ’ – среднее значение потенциала электрического поля внутри металла.
Таблица работа выхода электронов из простых веществ
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
|
Вещество |
Формула вещества |
Работа выхода электронов (W, эВ) |
|
серебро |
Ag |
4,7 |
|
алюминий |
Al |
4,2 |
|
мышьяк |
As |
4,79 — 5,11 |
|
золото |
Au |
4,8 |
|
бор |
B |
(4,60) |
|
барий |
Ba |
2,52 |
|
бериллий |
Be |
3,92 |
|
висмут |
Bi |
4,34 |
|
углерод (графит) |
C |
4,45 — 4,81 |
|
кальций |
Ca |
2,76 — 3,20 |
|
кадмий |
Cd |
4,04 |
|
церий |
Ce |
2,6 — 2,88 |
|
кобальт |
Co |
4,40 |
|
хром |
Cr |
4,60 |
|
цезий |
Cs |
1,94 |
|
медь |
Cu |
4,36 |
|
железо |
Fe |
4,40 — 4,71 |
|
галлий |
Ga |
3,96 — 4,16 |
|
германий |
Ge |
4,66 |
|
гафний |
Hf |
(3,53) |
|
ртуть |
Hg |
4,52 |
|
индий |
In |
(3,60 — 4,09) |
|
иридий |
Ir |
(4,57) |
|
калий |
K |
2,25 |
|
лантан |
La |
(3,3) |
|
литий |
Li |
2,49 |
|
магний |
Mg |
3,67 |
|
марганец |
Mn |
3,76 — 3,95 |
|
молибден |
Mo |
4,20 |
|
натрий |
Na |
2,28 |
|
ниобий |
Nb |
3,99 |
|
неодим |
Nd |
(3,3) |
|
никель |
Ni |
4,91 — 5,01 |
|
осмий |
Os |
(4,55) |
|
свинец |
Pb |
4,05 |
|
палладий |
Pd |
(4,98) |
|
празеодим |
Pr |
(2,7) |
|
платина |
Pt |
5,30 — 5,55 |
|
рубидий |
Rb |
2,13 |
|
рений |
Re |
4,98 |
|
родий |
Rh |
4,75 |
|
рутений |
Ru |
(4,52) |
|
сурьма |
Sb |
4,08 — 4,56 |
|
скандий |
Sc |
(3,2 — 3,33) |
|
селен |
Se |
4,86 |
|
кремний |
Si |
3,59 — 4,67 |
|
самарий |
Sm |
(3,2) |
|
олово (γ-форма) |
Sn |
4,38 |
|
олово (β-форма) |
Sn |
4,50 |
|
стронций |
Sr |
2,74 |
|
тантал |
Ta |
4,13 |
|
теллур |
Te |
4,73 |
|
торий |
Th |
3,35 — 3,47 |
|
титан |
Ti |
4,14 — 4,50 |
|
таллий |
Tl |
3,68 — 4,05 |
|
уран |
U |
3,27 — 4,32 |
|
ванадий |
V |
3,77 — 4,44 |
|
вольфрам |
W |
4,54 |
|
цинк |
Zn |
4,22 — 4,27 |
|
цирконий |
Zr |
3,96 — 4,16 |
Таблица работа выхода электронов из неорганических соединений
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
|
Вещество |
Формула вещества |
Работа выхода электронов (W, эВ) |
|
бромистое серебро |
AgBr |
~3,9 |
|
хлористое серебро |
AgCl |
~4,6 |
|
иодистое серебро |
AgI |
~4,0 |
|
сульфид серебра |
Ag2S |
~3,8 |
|
триоксид бора |
B2O3 |
4,7 |
|
оксид бария |
BaO |
1,0 — 1,6 |
|
барий вольфрамовокислый |
BaWO4 |
2,27 |
|
окись бериллия |
BeO |
3,8 — 4,7 |
|
окись кальция |
CaO |
1,8 — 2,4 |
|
ортовольфрамат кальция |
Ca3WO6 |
2,13 |
|
борид хрома |
CrB2 |
3,36 |
|
окись цезия |
Cs2O |
1,0 — 1,17 |
|
окись меди |
CuO |
4,35 — 5,34 |
|
закись меди |
Cu2O |
5,15 |
|
окись железа |
FeO |
3,85 |
|
вода |
H2O |
6,1 |
|
карбид гафния |
HfC |
2,04 |
|
оксид магния |
MgO |
3,1 — 4,4 |
|
диборид марганца |
MnB2 |
4,14 |
|
диборид молибдена |
MoB2 |
3,38 |
|
триоксид молибдена |
MoO3 |
4,25 |
|
силицид молибдена |
MoSi2 |
5,0 — 6,0 |
|
хлористый натрий |
NaCl |
4,2 |
|
борид ниобия |
NbB2 |
3,65 |
|
карбид ниобия |
NbC |
2,24 |
|
окись никеля |
NiO |
5,55 |
|
борид скандия |
ScB2 |
2,3 — 2,9 |
|
кремнезём |
SiO2 |
5,0 |
|
окись стронция |
SrO |
2,0 — 2,6 |
|
карбид тантала |
TaC |
3,05 — 3,14 |
|
пентаоксид тантала |
Ta2O5 |
4,65 |
|
дикарбид тория |
ThC2 |
3,5 |
|
оксид тория |
ThO2 |
2,54 — 2,67 |
|
сульфид титана |
TiS |
3,4 |
|
диборид титана |
TiB2 |
3,88 — 3,95 |
|
карбид титана |
TiC |
2,35 — 3,35 |
|
нитрид титана |
TiN |
2,92 |
|
окись титана |
TiO |
2,96 — 3,1 |
|
двуокись титана |
TiO2 |
4,7 |
|
карбид урана |
UC |
2,9 — 4,6 |
|
диборид ванадия |
VB2 |
3,88 — 3,95 |
|
диборид вольфрама |
WB2 |
2,62 |
|
диоксид вольфрама |
WO2 |
4,96 |
|
дисилицид вольфрама |
WSi2 |
5,0 — 6,0 |
|
борид циркония |
ZrB |
4,48 |
|
диборид циркония |
ZrB2 |
3,70 |
|
карбид циркония |
ZrC |
2,2 — 3,8 |
|
нитрид циркония |
ZrN |
2,92 |
_______________
Источник информации:
1. Landolt-Borstein’s Zahlenwerte und Funktionen aus Phsik, Chemie, Astrunumie, Geophysik, Thechnik, 6-е издание., Берлин, т. I, ч.4, 1955; т. II, ч.6, разд. 1, 1959.
2. В.С. Фоменко. Эмиссионные свойства элементов и химических соединений. Изд. АН УСССР, Киев, 1961.
Как
показывает опыт, свободные электроны
при обычных температурах практически
не, покидают металл. Следовательно, в
поверхностном слое металла должно быть
задерживающее электрическое поле,
препятствующее выходу электронов из
металла в окружающий вакуум. Работа,
которую нужно затратить для удаления
электрона из металла в вакуум, называется
работой
выхода. Укажем
две вероятные причины появления работы
выхода:
1. Если электрон
по какой-то причине удаляется из металла,
то в том месте, которое электрон покинул,
возникает избыточный положительный
заряд и электрон притягивается к
индуцированному им самим положительному
заряду.
2.
Отдельные электроны, покидая металл,
удаляются от него на расстояния порядка
атомных и создают тем самым над
поверхностью металла «электронное
облако», плотность которого быстро
убывает с расстоянием. Это облако
вместе с наружным слоем положительных
ионов решетки образует двойной
электрический слой, поле
которого подобно полю плоского
конденсатора. Толщина этого слоя равна
нескольким межатомным расстояниям
(10-10
— 10-9
м). Он не создает электрического поля
во внешнем пространстве, но препятствует
выходу свободных электронов из
металла.
Таким
образом, электрон при вылете из металла
должен преодолеть задерживающее его
электрическое поле двойного слоя.
Разность потенциалов
в этом слое, называемая поверхностным
скачком потенциала, определяется
работой выхода (А)
электрона
из металла:
=A/e,
где е
—
заряд электрона. Так как вне двойного
слоя электрическое поле отсутствует,
то потенциал среды равен нулю, а внутри
металла потенциал положителен и равен
.
Потенциальная энергия свободного
электрона внутри металла равна — е
и является относительно вакуума
отрицательной. Исходи из этого можно
167
считать,
что весь объем металла для электронов
проводимости представляет потенциальную
яму с плоским дном, глубина которой
равна работе выхода А.
Работа
выхода выражается в электрон-вольтах
(эВ):
1 эВ равен работе, совершаемой силами
поля при перемещении элементарного
электрического заряда (заряда, равного
заряду электрона) при прохождении
им разности потенциалов в 1 В. Так как
заряд электрона равен 1,6•l0-19
Кл,
то 1 эВ = 1,6•10-19
Дж.
Работа
выхода зависит от химической природы
металлов и от чистоты их поверхности
и колеблется в пределах нескольких
электрон-вольт (например, у калия
Л=2,2 эВ, у платины A
= б,3 эВ). Подобрав определенным образом
покрытие поверхности, можно значительно
уменьшить paботу
выхода. Например, если нанести на
поверхность вольфрама (А
=4,5
эВ) слой оксида щелочно-земельного
металла (Са, Sr,
Ba), то
работа выхода снижается до 2 эВ.
§ 105. Эмиссионные явления и их применение
Если
сообщить электронам в металлах энергию,
необходимую для преодоления работы
выхода, то часть электронов может
покинуть металл, в результате чего
наблюдается явление испускания
электронов, или электронной
эмиссии. В
зависимости от способа сообщения
электронам энергии различают
термоэлектронную, фотоэлектронную,
вторичную электронную и автоэлектронную
эмиссии.
1.
Термоэлектронная эмиссия — это
испускание электронов нагретыми
металлами. Концентрация свободных
электронов в металлах достаточно
высока, поэтому даже при средних
температурах вследствие распределения
электронов по скоростям (по энергии)
некоторые электроны обладают энергией,
достаточной для преодоления
потенциального барьера на границе
металла. С повышением температуры число
электронов, кинетическая энергия
теплового движения которых больше
работы выхода, растет и явление
термоэлектронной эмиссии становится
заметным.
Исследование
закономерностей термоэлектронной
эмиссии можно провести с помощью
простейшей двухэлектродной лампы —
вакуумного
диода, представляющего
собой откачанный баллон, содержащий
два электрода: катод К
и
анод А.
В
простейшем случае катодом служит
нить из тугоплавкого металла (например,
вольфрама), накаливаемая электрическим
током. Анод чаще всего имеет форму
металлического цилиндра, окружающего
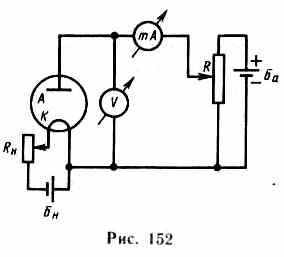
катод. Если диод включить в цепь, как
это показано на рис. 152, то при накаливании
катода и подаче на анод положительного
напряжения (относительно катода) в
анодной цепи диода возникает ток. Если
поменять полярность батареи Ба,
то ток прекращается, как бы сильно катод
ни накаливали. Следовательно, катод
испускает отрицательные частицы —
электроны.
Если
поддерживать температуру накаленного
катода постоянной и снять зависимость
анодного тока Iа
от анодного напряжения Ua
—
вольт-амперную
характеристику (рис.
153), то оказывается, что она не является
линейной, т. е. для вакуумного диода
закон Ома не выполняется. Зависимость
термоэлектронного тока I
от
анодного напряжения в области малых
168
положительных
значений U
описывается
законом
трех вторых (установлен
русским физиком С. А. Богуславским (1883—
1923) и американским физиком И. Ленгмюром
(1881 — 1957)):
I=BU3/2,
где В
— коэффициент,
зависящий от формы и размеров
электродов, а также их взаимного
расположения.
При
увеличении анодного напряжения ток
возрастает до некоторого максимального
значения Iнас,
называемого током
насыщения. Это
означает, что почти все электроны,
покидающие катод, достигают анода,
поэтому дальнейшее увеличение
напряженности поля не может привести
к увеличению термоэлектронного тока.
Следовательно, плотность тока насыщения
характеризует эмиссионную способность
материала катода.
Плотность
тока насыщения определяется формулой
Ричардсона — Дешмана, выведенной
теоретически на основе квантовой
статистики:
jнас=CT2e-A/(kT).
где А
— работа
выхода электронов из катода, Т
— термодинамическая
температура, С
—
постоянная, теоретически одинаковая
для всех металлов (это не подтверждается
экспериментом, что, по-видимому,
объясняется поверхностными эффектами).
Уменьшение работы выхода приводит к
резкому увеличению плотности тока
насыщения. Поэтому применяются
оксидные катоды (например, никель,
покрытый оксидом щелочно-земельного
металла), работа выхода которых равна
1 —1,5 эВ.
На
рис. 153 представлены вольт-амперные
характеристики для двух температур
катода: T1
и
Т2,
причем
T2>T1.
С
повышением температуры катода
испускание электронов с катода
интенсивнее, при этом увеличивается и
ток насыщения. При Ua=0
наблюдается
анодный ток, т. е. некоторые электроны,
эмиттируемые катодом, обладают энергией,
достаточной для преодоления работы
выхода и достижения анода без
приложения электрического поля.
Явление
термоэлектронной эмиссии используется
в приборах, в которых необходимо
получить поток электронов в вакууме,
например в электронных лампах,
рентгеновских трубках, электронных
микроскопах и т. д. Электронные лампы
широко применяются в электро- и
радиотехнике, автоматике и телемеханике
для выпрямления переменных токов,
усиления электрических сигналов и
переменных токов, генерирования
электромагнитных колебаний и т. д. В
зависимости от назначения в лампах
используются дополнительные управляющие
электроды.
2.
Фотоэлектронная эмиссия — это
эмиссия электронов из металла под
действием света, а также коротковолнового
электромагнитного излучения (например,
рентгеновского). Основные закономерности
этого явления будут разобраны при
рассмотрении фотоэлектрического
эффекта.
3.
Вторичная электронная эмиссия — это
испускание электронов поверхностью
металлов, полупроводников или диэлектриков
при бомбардировке их пучком электронов.
Вторичный электронный поток состоит
из электронов, отраженных поверхностью
(упруго и неупруго отраженные электроны),
и «истинно» вторичных электронов —
электронов, выбитых из металла,
полупроводника или диэлектрика
первичными электронами.
Отношение
числа вторичных электронов n2
к числу первичных п1,
вызвавших
эмиссию, называется коэффициентом
вторичной электронной эмиссии:
=n2/n1.
Коэффициент б
зависит от природы материала
поверхности, энергии бомбардирующих
частиц и их угла падения на поверхность.
У полупроводников и диэлектриков б
больше, чем у металлов. Это объясняется
тем, что в металлах, где концентрация
электронов проводимости велика,
вторичные электроны, часто сталкиваясь
с ними, теряют свою энергию и не могут
выйти из металла. В полупроводниках и
диэлектриках же из-за малой концентрации
электронов проводимости столкновения
вторичных электронов с ними происходят
гораздо реже и вероятность выхода
вторичных электронов из эмиттера
возрастает в несколько раз.
169
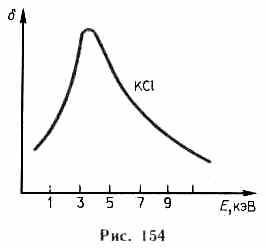
Для
примера на рис. 154 приведена качественная
зависимость коэффициента вторичной
электронной эмиссии б от энергии Е
падающих
электронов для KCl.
С увеличением энергии электронов б
возрастает, так как первичные электроны
все глубже проникают в кристаллическую
решетку и, следовательно, выбивают
больше вторичных электронов. Однако
при некоторой энергии первичных
электронов 6 начинает уменьшаться.
Это связано с тем, что с увеличением
глубины проникновения первичных
электронов вторичным все труднее
вырваться на поверхность. Значение
max
для KCl
достигает 12
(для чистых металлов оно не превышает
2).
Явление
вторичной электронной эмиссии
используется в фотоэлектронных
умножителях (ФЭУ),
применяемых для усиления слабых
электрических токов. ФЭУ представляет
собой вакуумную трубку с фотокатодом
К и анодом А, между которыми расположено
несколько электродов— эмиттеров
(рис.155).
Электроны, вырванные с фотокатода под
действием света, попадают на эмиттер
Э1,
пройдя
ускоряющую разность потенциалов между
К и Э1.
Из
эмиттера Э1
выбивается
электронов.
Усиленный таким образом
электронный
поток направляется на эмиттер Э2, и
процесс умножения повторяется на всех
последующих эмиттерах. Если ФЭУ содержит
n
эмиттеров,
то на аноде А, называемом коллектором,
получается
усиленный в б» раз фотоэлектронный
ток.
4.
Автоэлектронная эмиссия — это
эмиссия электронов с поверхности
металлов под действием сильного
внешнего электрического поля. Эти
явления можно наблюдать в откачанной
трубке, конфигурация электродов
которой (катод — острие, анод — внутренняя
поверхность трубки) позволяет при
напряжениях примерно 103
В получать электрические поля
напряженностью примерно 107
В/м. При постепенном повышении напряжения
уже при напряженности поля у поверхности
катода примерно 105—106
В/м возникает слабый ток, обусловленный
электронами, испускаемыми катодом. Сила
этого тока увеличивается с повышением
напряжения на трубке. Токи возникают
при холодном катоде, поэтому описанное
явление называется также холодной
эмиссией. Объяснение
механизма этого явления возможно лишь
на основе квантовой теории.
Соседние файлы в папке Трофимова Т.И. Курс физики
- #
02.05.2014155.65 Кб441.doc
- #
02.05.2014662.53 Кб6010.doc
- #
02.05.2014592.38 Кб3711.doc
- #
- #
02.05.2014181.76 Кб4613.doc
- #
02.05.2014336.38 Кб3914.doc
- #
02.05.2014206.34 Кб3615.doc
- #
02.05.2014169.98 Кб3716.doc
- #
02.05.2014123.39 Кб3617.doc
- #
02.05.2014629.25 Кб8218.doc
Высокая проводимость металлов обусловлена наличием в них электронов
проводимости, образующих электронный газ. Для оценки можно считать,
что каждый из атомов металлов, образующих кристаллическую решетку,
«отдает» в электронный газ несколько электронов (обычно от одного
до трех в зависимости от типа металла). Эти электроны уже не принадлежат
ионам решетки, а являются «общими» для всего объема металла. При
включении металлического проводника в электрическую цепь электроны
проводимости перемещаются, обеспечивая соответствующий ток проводимости.
Поскольку плотность металлов составляет примерно $10^{28div29}$
$frac{{атомов}}{{м}^{3}}$, то концентрация
(плотность) электронного газа очень высока. Это и объясняет высокую
электропроводность металлов.
Хотя электроны проводимости ведут себя в металле во многих отношениях
подобно газу (могут свободно перемещаться по всему объему металла,
их плотность испытывает тепловые флуктуации; что обуславливает так
называемый тепловой шум, и т.п.), но, чтобы выйти за пределы
объема металла, они должны совершить определенную работу, называемую
работой выхода. Если эта работа совершается за счет нагрева
металла, то процесс выхода электронов из металлов называется термоэлектронной
эмиссией.
Силы, по преодолению которых эмитированные электроны должны совершить
работу выхода, в простейшей модели (классическая модель Шоттки) описываются
двумя компонентами: двойным электрическим слоем на границе металла
с вакуумом и силами «изображения» (рис. 2).

В отсутствие внешних полей электронный газ «распространяется»
за поверхность металла на расстояния $x_{0}$ порядка межатомных,
и в этом поверхностном слое (его называют двойной слой) на электрон
действует некоторая сила $F_{0}$. Можно считать, что двойной слой
образует «плоский конденсатор», внешняя обкладка которого заряжена отрицательно. Поэтому силу $F_{0}$ можно принять постоянной $F_{0}=eE$ (рис. 2,в), где величина $E$ (напряженность поля двойного слоя)
зависит от плотности электронного газа и различна для разных металлов.
Когда электрон уходит на расстояния больше $x_{0}$, металл в целом
оказывается положительно заряженным, и действующую на электрон силу
можно определить как силу Кулона между электроном ($-e$) и его «зеркальным
изображением» ($+e$) (см. рис. 2, б):
$$
F_{im}=-frac{e^{2}}{4x^{2}},
$$
В точке $x_{0}$ эти силы должны «сшиваться» по величине, что
помогает определить величину силы $F_{0}$:
$$
F_{0}=left.F_{im}right|_{x_{0}}=-frac{e^{2}}{4x_{0}^{2}}.
$$
Общая работа сил, затрачиваемая на выход электрона из металла, определится
интегрированием по всему пространству вдоль направления $x$ от $0$
до $infty$:
$$
W_{p}=int_{0}^{infty}F(x)dx=frac{e^{2}}{4x_{0}}+int_{x_{0}}^{infty}frac{e^{2}}{4x^{2}}dx=frac{e^{2}}{2x},
$$
где $e$ — заряд электрона.
Величина работы выхода $W_{p}$ рассчитана исходя из классических соображений. Она называется полной работой выхода.
Реальные работы выхода $W_{a}$, измеряемые в экспериментах по термоэмиссии, оказались заметно меньше по величине. Это различие
было объяснено на базе квантовой физики.
Суть объяснения заключается в следующем. Плотность электронного газа
в металле весьма высока. Поэтому электроны проводимости нельзя считать
«свободными» в классическом смысле слова. Они представляют единую
квантовую систему. Согласно квантовым законам даже при абсолютном
нуле температуры все электроны системы не могут иметь одинаковую —
нулевую — энергию, поскольку в соответствии с квантовым запретом
Паули в одном квантовом состоянии (с данной энергией) может находиться
не более двух электронов, отличающихся проекцией спина. Распределение
электронов квантовой системы по энергиям в этом случае описывается
статистикой Ферми– Дирака.
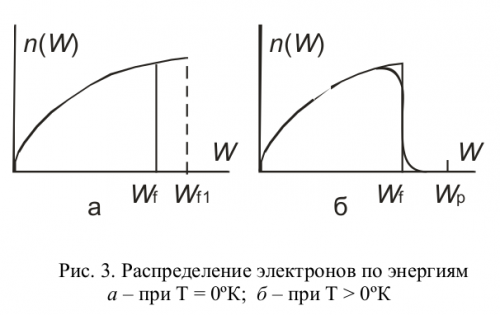
На рис. 3 изображен вид этого распределения для двух значений температуры:
$T=0^{circ}:{К}$ и $T>0^{circ}:{К}$. Максимальная
энергия $W_{f}$ при $0^{circ}:{К}$ называется уровнем
Ферми (энергией Ферми, химическим потенциалом идеального электронного
газа).
Поскольку при термоэмиссии металл покидают наиболее энергичные электроны,
имеющие энергию, близкую к энергии Ферми, то можно считать, что для
выхода им достаточно затратить лишь часть необходимой энергии, равной
разнице между $W_{p}$ и $W_{f}$:
$$
W_{a}=W_{p}-W_{f}=evarphi mbox{ или } varphi=frac{W_{a}}{e} .
$$
Здесь $e>0$ — элементарный заряд, а $W$ и $evarphi$ — работа
выхода. Её также часто выражают в электронвольтах (эВ)
(внесистемная единица широко принята в практике, 1 эВ — это работа (энергия), которую приобретает электрон, пройдя
без соударения разность потенциалов в 1 В. Чтобы пересчитать работу
выхода из эВ в единицы СИ или СГС, нужно умножить это значение на
заряд электрона в соответствующей системе единиц).
Величина энергии Ферми в металле $W_{f}$ зависит только от концентрации
электронов проводимости (от плотности электронного газа) и равна
$$
W_{f}=frac{h^{2}}{2m}left(frac{3n}{8pi}right)^{frac{2}{3}},
$$
где $n$ — концентрация,$m$ — масса электрона; $h$ — постоянная Планка.
Для различных металлов плотность электронного газа различна, поэтому
различен и уровень Ферми. Пунктиром на рис. 3,а показан уровень
Ферми $W_{f_1}$, соответствующий металлу с большей плотностью электронного
газа, чем у металла, характеризуемого сплошной линией. По порядку
величины уровень (энергия) Ферми для всех металлов примерно одинаков
и составляет несколько эВ:
Таблица 1. (Концентрация электронов проводимости $n$, уровни
Ферми $W_{f}$ и работа выхода различных металлов.)
| Металл | $ncdot10^{-28}$, $text{м}^{3}$ | $W_{f}cdot10^{19}$, Дж | $varphi,$ эВ |
| Th | 5,28 | 3,3 | |
| K | 1,33 | 3,55 | 2,22 |
| Cu | 8,4 | 7,04 | 4,4 |
| Ag | 5,9 | 4,3 | |
| W | 6,3 | 7,26 | 4,54 |
| Ni | 7,2 | 4,5 |
Назад к теме Ток в вакууме. Вакуумный диод или далее Модель потенциальной ямы (модель Шоттки)
Как показывает эксперимент, свободные электроны при обычных температурах практически не покидают металл, что свидетельствует о наличии в поверхностном слое задерживающего поля.
Работой выхода называется минимальная энергия, которую необходимо сообщить электрону, чтобы вывести его из твердого тела в вакуум.
С точки зрения классической физики наличие удерживающего поля объясняется возникновением на границе металла двойного электрического слоя, состоящего из положительных ионов и электронного облака, толщиной порядка 10-10-10-9м, которое препятствует вылету электронов.
Согласно зонной теории при температурах вблизи абсолютного нуля должны быть заполнены последовательно без промежутков все энергетические состояния электронов, начиная с уровня с наименьшей энергией, и существует резкая граница между заполненными и свободными уровнями.
При более высоких температурах эта граница размывается и ширина переходной зоны от практически полностью заполненных уровней до практически полностью свободных порядка kT.
Наивысший занятый электронами уровень называется уровнем Ферми, а соответствующая ему энергия – энергией Ферми (Или ЕF). Следовательно, работа выхода равна работе перемещения электрона с уровня Ферми за пределы твердого тела, т. е. определяется разностью энергии свободного электрона и его энергией на уровне Ферми:
(рис.205). В соответствии с этим говорят, что электроны внутри твердого тела находятся в потенциальной яме, глубина которой равна работе выхода.
РИС.205 РИС.206
На рис.205а представлена потенциальная яма для металлов, а на рис.205б – для диэлектриков. Ев и Еп — валентная и зона проводимости соответственно.
Работа выхода зависит от химического строения металла и чистоты поверхности. Она составляет 4,53 эВ для молибдена, 4,39 – для меди, 6,3 эВ – для платины, и может быть изменена нанесением покрытия на поверхность металла. Например, покрытие молибдена оксидом кальция или бария снижает работу выхода до 2,2 эВ.
В 1797 г. итальянский физик А. Вольта экспериментально установил, что если ряд металлов привести в контакт в определенной последовательности: Al, Zn, Sn, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd, то каждый предыдущий при соприкосновении с одним из последующих заряжается положительно. Этот ряд называется рядом Вольта, а возникающие контактные разности потенциалов составляют от нескольких десятых вольта до целых вольт.
Вольт экспериментально установил два закона для этого ряда последовательно соединенных металлов.
1.Контактная разность потенциалов зависит лишь от химического состава и температуры соприкасающихся металлов.
2.Контактная разность между концами ряда последовательно соединенных различных проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников и равна контактной разности потенциалов, возникающей при непосредственном соединении крайних проводников.
С точки зрения классической теории возникающая при контакте разность потенциалов обусловлена различиями в концентрации свободных электронов и разными работами выхода.
Согласно зонной теории при контакте двух металлов с различными работами выхода А1<А2, а следовательно, различными уровнями Ферми (рис.206а), происходит переход электронов с более высоких энергетических уровней на более низкие (рис.206б). Этот процесс продолжается до совпадения заполненных уровней, т. е. равенства энергии электронов в обоих металлах.
Между внутренними точками металлов, в контактном слое порядка 10-10м, возникает внутренняя разность потенциалов . Из равенства энергий электронов:
следует, что внутренняя разность потенциалов:
.
Между внешними не контактирующими поверхностями металлов возникает внешняя разность потенциалов, которую можно определить, выразив работу выхода для каждого металла как разность энергий электрона вне металла и внутри металла:
и
При контакте внутренние энергии равны и внешняя разность потенциалов . Измерить эту разность потенциалов для металлов находящихся в воздухе достаточно трудно из-за сорбции на поверхности ионов.
Необходимо отметить, что аналогичные процессы возникают при контактах металлов и с веществами, которые при реальных температурах относят к диэлектрикам или полупроводникам.
Вопрос 15 Электрический ток в металлах. Работа выхода.
Металлы в твёрдом состоянии имеют кристаллическую
структуру: расположение атомов в пространстве характеризуется периодической
повторяемостью и образует геометрически правильный рисунок, называемый кристаллической
решёткой.

электронов, которые могут перемещаться между ионами, находящимися в узлах
кристаллической решётки.
Газ свободных электронов в кристаллической решетке металла
представляет собой модель, показанную на. рисунке 15.1, где выделена траектория
одного из электронов.
Если
металлический проводник включить в замкнутую цепь, содержащую источник
тока, то
свободные
электроны продолжают Рисунок 15.1
совершать хаотическое тепловое движение, но
теперь — под действием возникшего внешнего электрического поля — они вдобавок
начнут перемещаться упорядоченно. Это направленное течение электронного
газа, накладывающееся на тепловое движение электронов, и есть электрический
ток в металле (поэтому свободные электроны называются также электронами
проводимости). Скорость упорядоченного движения электронов в металлическом
проводнике составляет приблизительно 0,1 мм/с.
О природе электрического тока в металлах было поставлено
множество опытов.
1) Опыт
Рикке
В 1901 году немецкий физик Э. Рикке поставил опыт,
доказывающий проводимость металлов за счёт свободных электронов.
В электрическую цепь были включены три прижатых друг к
другу цилиндра: два медных по краям и один алюминиевый между ними (рисунок
15.2). По этой цепи пропускался электрический ток в течение года.

Рисунок 15.2. Опыт Рикке
За год сквозь цилиндры прошёл заряд более трёх миллионов
кулон. Предположим, что каждый атом металла теряет по одному валентному
электрону, так что заряд иона равен элементарному заряду qe = 1,6·10-19
Кл Если ток создаётся движением положительных ионов, то нетрудно подсчитать
(сделайте это сами!), что такая величина прошедшего по цепи заряда
соответствует переносу вдоль цепи около 2кг меди.
Однако после разъединения цилиндров было обнаружено лишь
незначительное проникновение металлов друг в друга, обусловленное естественной
диффузией их атомов (и не более того). Электрический ток в металлах не
сопровождается переносом вещества, поэтому положительные ионы металла не
принимают участия в создании тока.
2) Опыты
Стюарта и Толмена
Прямое экспериментальное доказательство того, что
электрический ток в металлах создаётся движением свободных электронов, было
дано в опыте Т.Стюарта и Р.Толмена (1916 год).
Эксперименту Стюарта–Толмена предшествовали качественные
наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом
и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный
эффект: если резко затормозить

нём возникает кратковременный импульс тока. Эффект объясняется тем, что в
течение небольшого времени после торможения проводника его свободные заряды
продолжают двигаться по инерции.
Однако никаких
количественных результатов Мандельштам и Папалекси не получили, и
наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит
Стюарту и Толмену, которые не только наблюдали указанный электроинерционный
эффект, но и произвели необходимые измерения и расчёты.
Установка Стюарта и Толмена показана
на рисунке
15.3
Рисунок 15.3.
Катушка с большим числом витков металлического провода
приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью
скользящих контактов были подсоединены к специальному прибору — баллистическому
гальванометру, который позволяет измерять проходящий через него заряд.
После резкого торможения катушки в цепи возникал импульс
тока. Направление тока указывало на то, что он вызван движением отрицательных
зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по
цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе q/m.
Оно оказалось равно отношению заряда к массе электрона, которое в то время уже
было хорошо известно:
Так было окончательно выяснено, что носителями свободных
зарядов в металлах являются свободные электроны. Как видите, этот давно и
хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что
металлические проводники к тому моменту уже более столетия активно
использовались в самых разнообразных экспериментах по электромагнетизму
(сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако,
заключается в том, что сам электрон был открыт лишь в 1897 году).
На этой основе можно объяснить существование работы выхода
электронов из металла. Оказывается между металлом и вакуумом существует
контактная разность потенциалов. Так как в процессе движения электроны могут
покидать его, образуя «электронное облако». Часть электронов снова возвращается
в металл, другие снова его покидают. Явление очень похоже на испарение
жидкости. Толщина этого слоя равна нескольким межатомным расстояниям и
составляет d = (10-10 – 10-9) м. По вычислениям
контактная разность потенциалов составляет примерно φ = 1,4 В.
Для выхода электрона из металла тоже совершаться работа,
которая называется работой выхода. В вакууме работа выхода вычисляется по
формуле:
Для всех металлов работу выхода можно определить по
справочнику:

3) Классическая
электронная теория проводимости металлов
В 1900 году П.Друде создал классическую электронную теорию
проводимости металлов, которую затем развил Г. Лоренц. Согласно этой теории ,
электронный газ в металле рассматривается по аналогии с идеальным газом.
Основные положения теории:
1)
Свободные электроны в металлах ведут себя как молекулы идеального
газа и подчиняются его законам.
2)
Движение свободных электронов в металлах подчиняется законам
механики Ньютона.
3)
Свободные электроны в процессе хаотического движения сталкиваются
не между собой, а с ионами кристаллической решётки.
4)
При столкновении электронов с ионами, электроны передают свою
кинетическую энергию полностью.
Теория, построенная учёными является приближенной (грубой),
но объясняет многие законы электрического тока в металлах. Количественная
теория движения электронов в металле строиться на законах квантовой физики.
Решение задач
Задача 1 Сможет ли вылететь электрон из алюминия,
летящий со скоростью 8500 км/с, если работа выхода электрона из алюминия равна
4,25эВ (табличная величина)?
Дано: = 8500 км/с = 85·105
м/с, Авых = 4,25 эВ
Найти: сможет ли вылететь электрон
из алюминия — ?
Решение: для ответа на вопрос
необходимо сравнить кинетическую энергию электрона с работой выхода электрона
из металла, если Екин> Авых, то электрону хватит этой
кинетической энергии, чтобы вылететь из металла.
Переведём работу
выхода из электрон Вольт в Джоули Авых = 4,25 эВ = 4,25·1,6·10-19
= 6,8·10-19 Дж.
Найдём кинетическую энергию электрона:
Так как Екин>
Авых, значит электрон сможет вылететь из алюминия Ответ:
электрон сможет вылететь из алюминия.