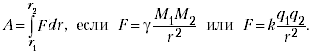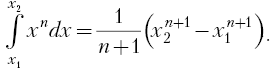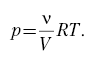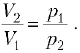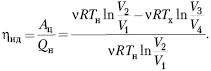Ранее мы достаточно плотно познакомились с процессами и методами работы с ними. Среди часто используемых способов работы с процессами выделяются два: уравнение Менделеева-Клапейрона (для описания состояния идеального газа) и первое начало термодинамики. Из нескольких друг за другом идущих разных процессов можно составить общий циклический процесс.
Круговой процесс (цикл) – составной термодинамический процесс, в результате совершения которого рабочее тело (газ) возвращается в исходное состояние. Таким образом, начальное и конечное состояние газа (давление газа , объём газа
и температура газа
) одинаковы. Попробуем изобразить такой процесс в координатах
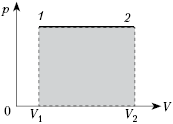
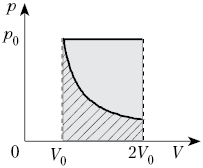
(рис. 1).
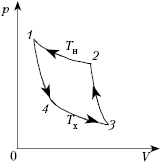
Рис. 1. Примеры циклических процессов
Например, наш циклический процесс 1.1 состоит из двух изохор, двух изотерм, а процесс 1.2 — из двух изобар и двух изохор. Таким образом, исходя из текстовых условий любой задачи и знания общего вида изопроцессов (именно из них чаще всего составляется цикл), можно нарисовать рисунок.
Для энергетического описания процесса (или цикла) через первое начало термодинамики необходимо обдумать два вопроса:
- как изменяется внутренняя энергия газа (
)
- чему равна работа газа (
)
- где
Для циклов есть небольшие фишки, которые удобно использовать для убыстрения задачи.
Так, изменение внутренней энергии газа зависит только от изменения температуры, а т.к. в цикле начальное и конечное состояние газа одинаково, то изменение внутренней энергии идеального газа за цикл равно 0 ().
Рис. 2. Графическая интерпретация работы газа
Поиск работы для газа также можно несколько упростить. Попробуем в координатах нарисовать график изобарического процесса и найти работу газа (рис. 2). Пусть газ находится в состоянии (давление
и объём
), далее газ изобарически перевели в состояние 2 (давление
и объём
). Тогда по определению работы газа:
(1)
Геометрически (рис. 2), произведение давления на разность объёмов численно равна площади прямоугольника, ограниченного сверху прямой (процессом), а снизу осью. В целом, эту логику можно расширить на любые процессы, тогда работа газа численно равна площади под кривой в координатах .
Также в рамках школьной физики присутствует условное деление циклов на прямые и обратные:
Прямой цикл – круговой, в котором рабочее тело совершает положительную работу за счёт сообщённой ему теплоты.
Обратный цикл — круговой, в котором рабочее тело совершает отрицательную работу.
Анализируя (1) вопрос о положительной и отрицательной работе, сводится к вопросу о соотношении между начальным и конечным объёмами, если:
Для графиков можно использовать следующую логику: в случае, если площадь под графиком расширения газа больше соответствующей площади для сжатия, значит цикл — прямой (рис. 3), если наоборот — обратный (рис. 4).
Рис. 3. Прямой циклический процесс
Рис. 4. Обратный циклический процесс
Таким образом, разница в прямом и обратном цикле может быть в очерёдности процессов. Так, прямой процесс, в нашем примере, — это 1-2-3-4-1, а обратный — 1-4-3-2-1.
Вывод: в задачах на циклические процессы нужно быть очень внимательным при прочтении, т.к. часть слов будет иметь глубокий физический смысл. Лучше всего процессы в таких задачах прорисовывать на графиках в координатах . Если график уже есть, то это к лучшему. Определяемся с конкретными изопроцессами, заданными в задаче, и используем это знание или через уравнение Менделеева-Клапейрона, или через первое начало термодинамики.
Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ «изыскивает внутренние резервы». Кроме того, работа численно равна площади под кривой процесса, а работа за цикл — площади внутри цикла.
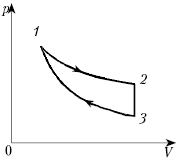
Задача 1.
На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки и
— адиабаты. Вычислите КПД
данной тепловой машины и максимально возможный КПД
.
К задаче 1
КПД тепловой машины можно вычислить как
Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:
Работа численно равна площади, ограниченной циклом. Поэтому
Участк и
по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» — то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и
,
и
, это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать
. Но, так как
, а
,то изменение внутренней энергии будет равно
Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке
:
Ответ: ,
.
Задача 2.
Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж. В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу
кДж. Найдите КПД данной тепловой машины.
К задаче 2
Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.
Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД
Ответ: .
Задача 3.
КПД тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе
кДж. Найдите разность
максимальной и минимальной температур газа в цикле.
К задаче 3
Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна
, а под кривой 3-1 —
. В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.
Ответ: 500 K.
Спецвыпуск
Г. А.
Белуха
Работа газа в термодинамике
··· Орловский выпуск ···
Г.А.БЕЛУХА,
школа № 4, г. Ливны, Орловская обл.
Работа газа в термодинамике
Методические рекомендации по
изучению темы, 10-й класс
При изучении работы газа в
термодинамике учащиеся неизбежно сталкиваются с
трудностями, обусловленными слабыми навыками
вычисления работы переменной силы. Поэтому к
восприятию этой темы необходимо готовиться,
начиная уже с изучения работы в механике и решая
с этой целью задачи на работу переменной силы
путём суммирования элементарных работ на всём
пути с помощью интегрирования.
Например, при вычислениях работы силы
Архимеда, силы упругости, силы всемирного
тяготения и т.п. надо учиться суммировать
элементарные величины с помощью простейших
дифференциальных соотношений типа dA = Fds.
Опыт показывает, что старшеклассники легко
справляются с этой задачей, – дугу траектории, на
которой сила увеличивается или уменьшается,
нужно разбить на такие промежутки ds, на
которых силу F можно считать постоянной
величиной, а затем, зная зависимость F = F(s),
подставить её под знак интеграла. Например,
Работа этих сил вычисляется с помощью
простейшего табличного интеграла
Такая методика облегчает адаптацию
будущих студентов к восприятию курса физики в
вузе и устраняет методические сложности,
связанные с умением находить работу переменной
силы в термодинамике и др.
После того как учащиеся усвоили, что
такое внутренняя энергия и как найти её
изменение, целесообразно дать обобщающую схему:
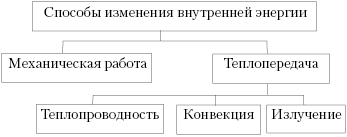
Усвоив, что работа – это один из
способов изменения внутренней энергии,
десятиклассники легко рассчитывают работу газа
в изобарном процессе. На данном этапе необходимо
подчеркнуть, что сила давления газа на всём пути
не меняется, и по третьему закону Ньютона |F2| = |F1|,
знак работы находим из формулы A = Fs cos. Если
= 0°, то A > 0,
если = 180°,
то A < 0. На графике зависимости р(V)
работа численно равна площади под графиком.
Пусть газ расширяется или сжимается
изотермически. Например, газ сжимается под
поршнем, давление изменяется, и в любой момент
времени
При бесконечно малом перемещении
поршня на dl мы получим бесконечно малое
изменение объёма dV, а давление р можно
считать постоянным. По аналогии с нахождением
механической работы переменной силы, составим
простейшее дифференциальное соотношение dA = pdV,
тогда 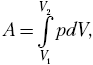
зависимость р (V), запишем 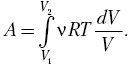
типа 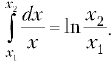
газа в этом случае отрицательна, т.к. = 180°:
т.к. V2 < V1.
Полученную формулу можно переписать,
используя соотношение
Для закрепления решим задачи.
1. Газ переходит из состояния 1
(объём V1, давление р1) в
состояние 2 (объём V2, давление р2)
в процессе, при котором его давление зависит от
объёма линейно. Найдите работу газа.
Решение. Построим примерный
график зависимости p от V. Работа равна
площади под графиком, т.е. площади трапеции:
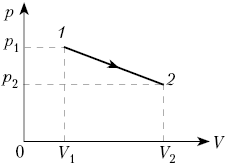
2. Один моль воздуха, находящийся при
нормальных условиях, расширяется от объёма V0
до 2V0 двумя способами – изотермически
и изобарно. Сравните работу, совершённую
воздухом в этих процессах.
Решение
При изобарном процессе Ap = р0V, но р0 =
RT0/V0,
V = V0,
следовательно, Ap = RT0.
При изотермическом процессе:
Сравним:
Изучив первый закон термодинамики и
его применение к изопроцессам и закрепив
решением задач тему о работе в термодинамике,
учащиеся подготовились к восприятию наиболее
сложной части термодинамики «Работа циклов и КПД
тепловых машин». Этот материал я излагаю в
следующей последовательности: работа циклов –
цикл Карно – КПД тепловых машин – круговые
процессы.
процессом (или циклом) называется
термодинамический процесс, в результате
которого тело, пройдя ряд состояний,
возвращается в исходное состояние. Если все
процессы в цикле равновесные, то цикл считается
равновесным. Его можно изобразить графически в
виде замкнутой кривой.
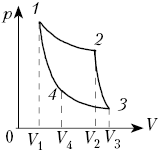
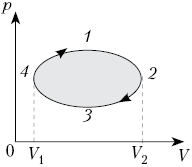
На рисунке показан график зависимости
давления p от объёма V (диаграмма p, V)
для некоторого цикла 1–2–3–4–1. На участках 1–2
и 4–1 газ расширяется и совершает
положительную работу А1, численно
равную площади фигуры V1412V2.
На участке 2–3–4 газ сжимается и совершает
работу А2, модуль которой равен
площади фигуры V2234V1. Полная
работа газ за цикл А = А1 + А2,
т.е. положительна и равна площади фигуры 12341.
Если равновесный цикл изображается
замкнутой кривой на р, V-диаграмме,
которая обходится по часовой стрелке, то работа
тела положительна, а цикл накзывается прямым.
Если замкнутая кривая на р, V-диаграмме
обходится против часовой стрелки, то газ
совершает отрицательную работу за цикл, а цикл
называется обратным. В любом случае модуль
работы газа за цикл равен площади фигуры,
ограниченной графиком цикла на р, V-диаграмме.
В круговом процессе рабочее тело
возвращается в исходное состояние, т.е. в
состояние с первоначальной внутренней энергией.
Это значит, что изменение внутренней энергии за
цикл равно нулю: U = 0.
Так как, по первому закону термодинамики, для
всего цикла Q = U + A, то Q = A.
Итак, алгебраическая сумма всех количеств
теплоты, полученных за цикл, равна работе тела за
цикл: Aц = Qн + Qх = Qн
– |Qх|.
Рассмотрим один из круговых процессов
– цикл Карно. Он состоит из двух изотермических и
двух адиабатических процессов. Пусть рабочим
телом является идеальный газ. Тогда на участке 1–2
изотермического расширения, согласно первому
закону термодинамики, всё получаемое газом тепло
идёт на совершение положительной работы: Q12 = A12.
То есть нет никаких потерь тепла в окружающее
пространство и никакого изменения внутренней
энергии: U = 0,
т.к. T12 = const (потому что газ –
идеальный).
На участке 2–3 адиабатного
расширения газ совершает положительную работу
за счёт изменения внутренней энергии, т.к. Qад = 0
= U23 + Aг23
Aг23 = –
U23.
Здесь также нет потерь тепла, по определению
адиабатного процесса.
На участке 3–4 над газом
совершается положительная работа внешней силой,
но он не нагревается (изотермический процесс).
Благодаря достаточно медленно протекающему
процессу и хорошему контакту с холодильником газ
успевает отдавать получаемую за счёт работы
энергию в виде тепла холодильнику. Сам же газ
совершает при этом отрицательную работу: Q34 = Aг34
< 0.
На участке 4–1 газ адиабатно (без
теплообмена) сжимается до исходного состояния.
При этом он совершает отрицательную работу, а
внешние силы – положительную: 0 = U41 + Aг41
Aг41 = –
U41.
Таким образом, за цикл газ получает
тепло только на участке 1–2, изотермически
расширяясь:
Холодильнику тепло отдаётся только
при изотермическом сжатии газа на участке 3–4:
Согласно первому закону термодинамики
Aц = Qн – |Qx|;
поэтому
КПД машины, работающей по циклу Карно,
найдём по формуле
Согласно закону Бойля–Мариотта для
процессов 1–2 и 3–4, а также уравнению
Пуассона для процессов 2–3 и 4–1, легко
доказать, что
(Хорошо бы увидеть, как автор это
делает: ведь уравнение Пуассона для диабаты
идеального газа надо ещё получить. – Ред.)
После сокращений получим формулу КПД
тепловой машины, работающей по циклу Карно:
обратному циклу, методически правильно, как
показывает опыт, изучать на примере работы
обратного цикла Карно, т.к. он обратим и его можно
провести в обратном направлении: расширять газ
при понижении температуры от Tн до Tx
(процесс 1–4) и при низкой температуре Tx
(процесс 4–3), а затем сжимать (процессы 3–2
и 2–1). Теперь двигатель совершает работу,
чтобы привести в действие холодильную машину.
Рабочее тело отнимает количество теплоты Qx
у продуктов внутри при низкой температуре Tх,
а отдаёт количество теплоты Qн
окружающим телам, за пределами холодильника, при
более высокой температуре Tн. Таким
образом, машина, работающая по обратному циклу
Карно, уже не тепловая, а идеальная холодильная.
Роль нагревателя (отдающего тепло) выполняет
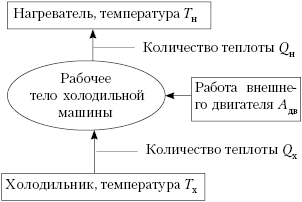
тело с более низкой температурой. Но, сохранив
названия элементов, как в тепловой машине,
работающей по прямому циклу, мы можем
представить блок-схему холодильника в следующем
виде:
Обратим внимание, что тепло от
холодного тела переходит в холодильной машине к
телу с более высокой температурой не
самопроизвольно, а за счёт работы внешней силы.
Важнейшей характеристикой
холодильника является холодильный коэффициент , определяющий
эффективность работы холодильника и равный
отношению количества теплоты, отнятого от
холодильной камеры Qх к затраченной
энергии внешнего источника
За один обратный цикл рабочее тело
получает от холодильника количество теплоты Qх
и отдаёт в окружающее пространство количество
теплоты Qн, что больше Qх на
работу Aдв, совершаемую
электродвигателем над газом за цикл: |Qн| = |Qх| + Адв.
Энергия, затраченная двигателем
(электроэнергия в случае компрессорных
электрических холодильников), идёт на полезную
работу над газом, а также на потери при
нагревании обмоток двигателя электрическим
током QR и на трение в схеме Атр.
Если пренебречь потерями на трение и
джоулево тепло в обмотках двигателя, то
холодильный коэффициент
Учитывая, что в прямом цикле
после несложных преобразований
получим:
Последнее соотношение между
холодильным коэффициентом и КПД тепловой машины,
которая может работать и по обратному циклу,
показывает, что холодильный коэффициент может
быть больше единицы. В этом случае тепла
отнимается от холодильной камеры и возвращается
в комнату больше, чем для этого используется
энергии двигателем.
В случае идеальной тепловой машины,
работающей по обратному циклу Карно (идеального
холодильника), холодильный коэффициент имеет
максимальное значение:
В реальных холодильниках т.к. не вся получаемая
двигателем энергия идёт на работу над рабочим
телом, о чём написано выше.
Решим задачу:
• Оцените стоимость изготовления 1 кг
льда в домашнем холодильнике, если температура
испарения фреона –tх °С,
температура радиатора tн °С.
Стоимость одного киловатт-часа электроэнергии
равна Ц. Температура в комнате t.
Дано:
m, c, t, tн, tх,
, Ц.
____________
Д – ?
Решение
Стоимость Д изготовления льда равна
произведению работы электродвигателя на тариф Ц:
Д = ЦА.
Для превращения воды в лёд с
температурой 0 °С необходимо отвести от неё
количество теплоты Q = m(ct + ). Считаем
приближённо, что над фреоном совершается
обратный цикл Карно с изотермами при
температурах Tн и Tх.
Используем формулы для холодильного
коэффициента: по определению, = Q/A и для
идеального холодильника ид = Tх/(Tн – Tх).
Из условия следует, что
ид.
Решаем совместно три последних
уравнения:
Разбирая с учащимися эту задачу,
необходимо обратить внимание на то, что основная
работа холодильного устройства идёт не на
охлаждение продуктов, а на поддержание
температуры внутри холодильного шкафа путём
периодической откачки тепла, проникающего
сквозь стенки холодильника.
Для закрепления темы можно решить
задачу:
• КПД тепловой машины, работающей по
циклу, состоящему из изотермического процесса 1–2,
изохорического 2–3 и адиабатического 3–1,
равен , а
разность максимальной и минимальной температур
газа в цикле равна T. Найдите работу, совершённую
моль одноатомного
идеального газа в изотермическом процессе.
Решение
При решении задач, в которых
фигурирует КПД цикла, полезно предварительно
проанализировать все участки цикла, используя
первый закон термодинамики, и выявить участки,
где тело получает и отдаёт тепло. Проведём
мысленно ряд изотерм на р, V-диаграмме.
Тогда станет ясно, что максимальная температура
в цикле на изотерме, а минимальная – в т. 3.
Обозначим их через T1 и T3
соответственно.
На участке 1–2 изменение
внутренней энергии идеального газа U2 – U1 = 0.
По первому закону термодинамики, Q12 = (U2 – U1) + А12.
Так как на участке 1–2 газ расширялся, то
работа газа А12 > 0. Значит, и
подведённое к газу количество теплоты на этом
участке Q12 > 0, причём Q12 = А12.
На участке 2–3 работа газа равна
нулю. Поэтому Q23 = U3 – U2.
Воспользовавшись выражениями U2=
cVT1
и тем, что T1 – T3 = T, получим Q23 = –
cV
T < 0.
Это означает, что на участке 2–3 газ получает
отрицательное количество теплоты, т.е. отдаёт
тепло.
На участке 3–1 теплообмена нет,
т.е. Q31 = 0 и, по первому закону
термодинамики, 0 = (U1 – U3) + A31.
Тогда работа газа
A31 = U3 – U1 = cV(T3 –T1) = –
cV
T.
Итак, за цикл газ совершил работу A12 + А31 = А12 – cV
T и получил
тепло только на участке 1–2. КПД цикла
Так как то работа газа на изотерме равна
Геннадий Антонович Белуха –
заслуженный учитель РФ, педагогический стаж 20
лет, ежегодно его ученики занимают призовые
места на различных этапах всероссийской
олимпиады по физике. Хобби – компьютерная
техника.
Физика, 10 класс
Урок 25. Тепловые двигатели. КПД тепловых двигателей
Перечень вопросов, рассматриваемых на уроке:
1) Понятие теплового двигателя;
2)Устройство и принцип действия теплового двигателя;
3)КПД теплового двигателя;
4) Цикл Карно.
Глоссарий по теме
Тепловой двигатель – устройство, в котором внутренняя энергия топлива превращается в механическую.
КПД (коэффициент полезного действия) – это отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.
Двигатель внутреннего сгорания – двигатель, в котором топливо сгорает непосредственно в рабочей камере (внутри) двигателя.
Реактивный двигатель – двигатель, создающий необходимую для движения силу тяги посредством преобразования внутренней энергии топлива в кинетическую энергию реактивной струи рабочего тела.
Цикл Карно – это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов.
Нагреватель – устройство, от которого рабочее тело получает энергию, часть которой идет на совершение работы.
Холодильник – тело, поглощающее часть энергии рабочего тела (окружающая среда или специальные устройства для охлаждения и конденсации отработанного пара, т.е. конденсаторы).
Рабочее тело — тело, которое расширяясь, совершает работу (им является газ или пар)
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 269 – 273.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа,2014. – С. 87 – 88.
Открытые электронные ресурсы по теме урока
http://kvant.mccme.ru/1973/12/teplovye_mashiny.htm
Теоретический материал для самостоятельного изучения
Сказки и мифы разных народов свидетельствуют о том, что люди всегда мечтали быстро перемещаться из одного места в другое или быстро совершать ту или иную работу. Для достижения этой цели нужны были устройства, которые могли бы совершать работу или перемещаться в пространстве. Наблюдая за окружающим миром, изобретатели пришли к выводу, что для облегчения труда и быстрого передвижения нужно использовать энергию других тел, к примеру, воды, ветра и т.д. Можно ли использовать внутреннюю энергию пороха или другого вида топлива для своих целей? Если мы возьмём пробирку, нальём туда воду, закроем её пробкой и будем нагревать. При нагревании вода закипит, и образовавшие пары воды вытолкнут пробку. Пар расширяясь совершает работу. На этом примере мы видим, что внутренняя энергия топлива превратилась в механическую энергию движущейся пробки. При замене пробки поршнем способным перемещаться внутри трубки, а саму трубку цилиндром, то мы получим простейший тепловой двигатель.
Тепловой двигатель – тепловым двигателем называется устройство, в котором внутренняя энергия топлива превращается в механическую.
Вспомним строение простейшего двигателя внутреннего сгорания. Двигатель внутреннего сгорания состоит из цилиндра, внутри которого перемещается поршень. Поршень с помощью шатуна соединяется с коленчатым валом. В верхней части каждого цилиндра имеются два клапана. Один из клапанов называют впускным, а другой – выпускным. Для обеспечения плавности хода поршня на коленчатом вале укреплен тяжелый маховик.
Рабочий цикл ДВС состоит из четырех тактов: впуск, сжатие, рабочий ход, выпуск.
Во время первого такта открывается впускной клапан, а выпускной клапан остается закрытым. Движущийся вниз поршень засасывает в цилиндр горючую смесь.
Во втором такте оба клапана закрыты. Движущийся вверх поршень сжимает горючую смесь, которая при сжатии нагревается.
В третьем такте, когда поршень оказывается в верхнем положении, смесь поджигается электрической искрой свечи. Воспламенившаяся смесь образует раскаленные газы, давление которых составляет 3 -6 МПа, а температура достигает 1600 -2200 градусов. Сила давления толкает поршень вниз, движение которого передается коленчатому валу с маховиком. Получив сильный толчок маховик будет дальше вращаться по инерции, обеспечивая движение поршня и при последующих тактах. Во время этого такта оба клапана остаются закрытыми.
В четвертом такте открывается выпускной клапан и отработанные газы движущимся поршнем выталкиваются через глушитель (на рисунке не показан) в атмосферу.
Любой тепловой двигатель включает в себя три основных элемента: нагреватель, рабочее тело, холодильник.
Для определения эффективности работы теплового двигателя вводят понятие КПД.
Коэффициентом полезного действия называют отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.
Q1 – количество теплоты полученное от нагревания
Q2 – количество теплоты, отданное холодильнику

Этот КПД является реальным, т.е. как раз эту формулу и используют для характеристики реальных тепловых двигателей.
Зная мощность N и время работы t двигателя работу, совершаемую за цикл можно найти по формуле

Передача неиспользуемой части энергии холодильнику.
В XIX веке в результате работ по теплотехнике французский инженер Сади Карно предложил другой способ определения КПД (через термодинамическую температуру).
Главное значение этой формулы состоит в том, что любая реальная тепловая машина, работающая с нагревателем, имеющим температуру Т1, и холодильником с температурой Т2, не может иметь КПД, превышающий КПД идеальной тепловой машины. Сади Карно, выясняя при каком замкнутом процессе тепловой двигатель будет иметь максимальный КПД, предложил использовать цикл, состоящий из 2 адиабатных и двух изотермических процессов
Цикл Карно — самый эффективный цикл, имеющий максимальный КПД.
Не существует теплового двигателя, у которого КПД = 100% или 1.
Формула дает теоретический предел для максимального значения КПД тепловых двигателей. Она показывает, что тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Лишь при температуре холодильника, равной абсолютному нулю, η = 1.
Но температура холодильника практически не может быть ниже температуры окружающего воздуха. Повышать температуру нагревателя можно. Однако любой материал (твердое тело) обладает ограниченной теплостойкостью, или жаропрочностью. При нагревании он постепенно утрачивает свои упругие свойства, а при достаточно высокой температуре плавится.
Сейчас основные усилия инженеров направлены на повышение КПД двигателей за счет уменьшения трения их частей, потерь топлива вследствие его неполного сгорания и т. д. Реальные возможности для повышения КПД здесь все еще остаются большими.
Повышение КПД тепловых двигателей и приближение его к максимально возможному — важнейшая техническая задача.
Тепловые двигатели – паровые турбины, устанавливают также на всех АЭС для получения пара высокой температуры. На всех основных видах современного транспорта преимущественно используются тепловые двигатели: на автомобильном – поршневые двигатели внутреннего сгорания; на водном – двигатели внутреннего сгорания и паровые турбины; на железнодорожном – тепловозы с дизельными установками; в авиационном – поршневые, турбореактивные и реактивные двигатели.
Сравним эксплуатационные характеристики тепловых двигателей.
КПД:
Паровой двигатель – 8%.
Паровая турбина – 40%.
Газовая турбина – 25-30%.
Двигатель внутреннего сгорания – 18-24%.
Дизельный двигатель – 40– 44%.
Реактивный двигатель – 25%.
Широкое использование тепловых двигателей не проходит бесследно для окружающей среды: постепенно уменьшается количество кислорода и увеличивается количество углекислого газа в атмосфере, воздух загрязняется вредными для здоровья человека химическими соединениями. Возникает угроза изменения климата. Поэтому нахождение путей уменьшения загрязнения окружающей среды является сегодня одной из наиболее актуальных научно-технических проблем.
Примеры и разбор решения заданий
1. Какую среднюю мощность развивает двигатель автомобиля, если при скорости 180 км/ч расход бензина составляет 15 л на 100 км пути, а КПД двигателя 25%?
Дано: v=180км/ч = 50 м/с, V = 15 л = 0,015 м3, s = 100 км = 105 м, ɳ = 25% = 0,25, ρ = 700 кг/м3, q = 46 × 106 Дж/кг.
Найти: N.
Решение:
Запишем формулу для расчёта КПД теплового двигателя:
Работу двигателя, можно найти, зная время работы и среднюю мощность двигателя:
Количество теплоты, выделяющееся при сгорании бензина, находим по формуле:
Учитывая всё это, мы можем записать:

Время работы двигателя можно найти по формуле:
Из формулы КПД выразим среднюю мощность:

Подставим числовые значения величин:
После вычислений получаем, что N=60375 Вт.
Ответ: N=60375 Вт.
2. Тепловая машина имеет КПД 25 %. Средняя мощность передачи теплоты холодильнику составляет 4 кВт. Какое количество теплоты рабочее тело получает от нагревателя за 20 с?
Дано: ɳ = 25%, N = 4000 Вт, t = 20 с.
Найти: Q1.
Решение



§7. Круговые процессы (циклы)
называется термодинамический процесс с телом, в результате совершения которого тело, пройдя через ряд состояний, возвращается в исходное состояние.
Если все процессы в цикле равновесные, то цикл считается равновесными. Его можноизобразить графически, и получится замкнутая кривая. На рис. 7 показан график зависимости давления `p` от объёма `V` (диаграмма $$ p-V$$) для некоторого цикла `1–2–3–4–1`, совершаемого газом. На участке `4–1–2` газ расширяется и совершает положительную работу `A_1`, численно равную площади фигуры $$ {V}_{1}412{V}_{2}$$. На участке `2–3–4` газ сжимается и совершает отрицательную работу $$ {A}_{2}$$, модуль которой равен площади фигуры $$ {V}_{2}234{V}_{1}$$. Полная работа газа за цикл $$ A={A}_{1}+{A}_{2}$$, т. е. положительна и равна площади фигуры `1–2–3–4–1`, изображающей цикл на диаграмме $$ p-V$$.
называется круговой процесс, в котором тело совершает положительную работу за цикл. Прямой равновесный цикл на диаграмме $$ p-V$$ изображается замкнутой кривой, которая обходится по часовой стрелке. Пример прямого цикла дан на рис. 7.
называется круговой процесс, в котором тело совершает отрицательную работу за цикл. На диаграмме $$ p-V$$ замкнутая кривая равновесного обратного цикла обходится против часовой стрелки.
В любом равновесном цикле работа за цикл равна по модулю площади фигуры, ограниченной кривой на диаграмме $$ p-V$$.
В круговом процессе тело возвращается в исходное состояние, т. е. в состояние с первоначальной внутренней энергией. Это значит, что изменение внутренней энергии за цикл равно нулю: $$ ∆U=0$$. Так как по первому закону термодинамики для всего цикла $$ Q=∆U+A$$, то $$ Q=A$$. Итак, алгебраическая сумма всех количеств теплоты, полученной телом за цикл, равна работе тела за цикл.
На некоторых участках прямого цикла тело получает от окружающих тел количество теплоты $$ {Q}^{+}$$ $$ ({Q}^{+}>0)$$, а на некоторых отдаёт $$ {Q}^{-}$$ т. е. получает отрицательное количество теплоты `«-Q^(-)»` `(Q^(-)>0)`.
За цикл тело совершает положительную работу `A`.
Коэффициентом полезного действия прямого цикла называется величина $$ eta ={displaystyle frac{A}{{Q}^{+}}}$$.
Поскольку $$ A={Q}^{+}+(-{Q}^{-})$$, то
$$ eta ={displaystyle frac{{Q}^{+}-{Q}^{-}}{{Q}^{+}}}=1-{displaystyle frac{{Q}^{-}}{{Q}^{+}}}$$. (20)
Для обратного цикла коэффициент полезного действия не вводится.