Как найти работу зная силу упругости

Сила упругости, как и
сила тяжести, является консервативной. Напомним, что консервативная сила —
это такая сила, работа которой при движении тела по замкнутому контуру, равна
нулю. В одном из уроков мы уже убедились, что работу силы упругости нельзя
вычислить, пользуясь общей формулой для работы силы. Дело в том, что сила
упругости изменяется с изменением растяжения или сжатия пружины. Поэтому нам
необходимо будет воспользоваться графиком зависимости силы упругости от
удлинения.

Поскольку сила упругости
линейно зависит от удлинения, нам не составит труда найти площадь под графиком
функции силы упругости. Эта площадь и будет являться работой. На графике
зависимости силы упругости от удлинения обозначим два произвольных значения
силы: F₁
и F₂.
Этим значениям будут соответствовать значения удлинения х₁ и х₂.
Как видно из графика, чтобы найти работу, нам нужно вычислить площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований и высоты. Очевидно, что
основания — это F₁
и F₂,
а высота равна х₁ − х₂. Тогда,
используя формулу для силы упругости, мы можем вывести окончательное выражение
для работы силы упругости:

Напомним, что изучая
работу силы, мы пришли к выводу, что работа равна изменению кинетической
энергии. В данном случае мы видим, что работа силы упругости равна изменению
потенциальной энергии пружины. Но о потенциальной энергии мы поговорим
немного позже.

Итак, мы выяснили, что работа
силы упругости, так же, как и работа силы тяжести, не зависит от траектории
движения.

Пример решения задачи.

Задача.
Когда пружину, изначально находящуюся в расслабленном состоянии, растянули на 2
см, сила упругости составила 5 Н. Найдите работу силы упругости при растяжении этой
пружины на 8 см.

Введение

На прошлом уроке мы с вами показали, что для применения теоремы об изменении кинетической энергии мы должны уметь вычислять работу основных сил в природе. И мы уже научились это делать на примере работы силы тяжести. Было показано, что эту величину очень просто рассчитать, если ввести в рассмотрение новый вид энергии – потенциальную энергию тела, притягивающуюся к земле. Сегодня сделаем то же самое для силы упругости.

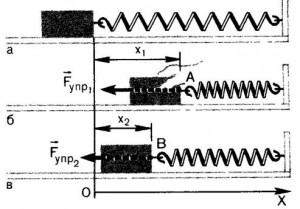
Рассмотрим простую систему: массивный груз, прикрепленный к пружине (см. рис. 1).

Рис. 1. Груз, прикрепленный к пружине

Пусть изначально система находится в состоянии равновесия, то есть пружина не деформированная, и груз покоится. Выведем эту систему из равновесия и сделаем так, чтобы пружина стала в сжатом состоянии (см. рис. 2).

Рис. 2. Система выведена из равновесия

Если направить ось ОХ так, как показано на рис. 2, и расположить начало координат там, где до начала сжатия был расположен центр груза, то проекцию возникающей силы упругости на нашу ось ОХ можно записать в виде:

,

где k – жесткость пружины, величина деформации пружины. Если предоставить пружину самой себе, то груз будет смещаться влево, при этом сила упругости будет совершать работу. Предположим, что левый конец пружины вместе с грузом переместился из положения А в положение В (см. рис. 3).

Рис. 3. Перемещение груза

В этом положении деформация пружины равна уже не , а . А перемещение конца пружины и одновременно перемещение центра груза равно разности координат . Попытаемся вычислить работу силы упругости, совершенную при таком движении груза.

Вычисление работы силы упругости

Груз совершил известное перемещение, величину силы упругости мы также знаем, векторы перемещения и силы упругости параллельны. Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.

О чем нам говорит формула, которая выражает величину силы упругости? О том, что сила упругости – величина не постоянная, она меняется по мере перемещения груза. И действительно, величина этой силы, как мы видим из формулы, зависит от координаты центра груза. Формула же для работы силы, которую мы применяли раньше, справедлива лишь в том случае, если сила не меняет свою величину по мере движения. Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.

Можно всю траекторию движения груза разбить на очень маленькие участки (участки, в пределах которых силу упругости можно считать практически постоянной). Далее в пределах каждого такого участка мы можем рассчитать работу силы упругости ввиду ее практического постоянства. Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.

Рис. 4. Зависимость силы упругости от координаты движения

Видно, что если отложить на графике зависимость модуля силы упругости от модуля координаты груза, затем проделать описанное выше разбиение на маленькие участки, то величина работы на каждом маленьком участке численно равна площади фигуры, ограниченной графиком: осью абсцисс и двумя перпендикулярами к этой оси (см. рис. 5).

Рис. 5. Площадь фигуры

Если просуммировать значение работы на каждом участке (площадь маленьких фигур), то получим площадь большой фигуры, показанной на рис. 6.

Рис. 6. Площадь большой фигуры

Поскольку данная фигура является прямоугольной трапецией, то мы можем воспользоваться формулой для расчета площади такой фигуры – это полусумма оснований, умноженная на высоту. В результате преобразований получим такую формулу – работа равна разности между величиной:

К этому результату можно прийти и несколько иным способом. Для вычисления работы силы упругости в этом способе необходимо просто взять среднее значение силы упругости и умножить его на перемещение тела. Это утверждение можно записать как:

,

где  среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение  подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:

Как видно из этой формулы, работа зависит лишь от начальной и конечной координаты центра груза, и еще одно замечание: как видно из последней формулы, работа силы упругости никоим образом не зависит от массы груза. Это обусловлено тем, что и сама сила упругости не зависит от этой массы.

Теперь внимательнее посмотрим на последнюю формулу – если вынести -1 за скобки, то получим, что работа есть взятая со знаком минус разность между значениями некоторой величины, равной половине произведения жесткости пружины на квадрат ее удлинения в конечный и начальный моменты времени.

Вспомним, как мы поступили при расчете работы силы тяжести на прошлом уроке. В тот раз мы столкнулись с новой для нас физической величиной, разность между значениями которой в конечной и начальной моменты времени равнялась взятой со знаком « — » работе силы тяжести. Это величина, равная произведению массы тела на ускорение свободного падения и высоту, на которую было поднято тело над некоторым уровнем, мы назвали потенциальной энергией тела, поднятого над землей.

Потенциальная энергия упруго деформированного тела

Здесь поступим аналогичным образом. Величину, равную половине произведения жесткости пружины на квадрат ее удлинения, назовем потенциальной энергией деформированной пружины. Мы имеем право это сделать, поскольку изменение данной величины, взятой с обратным знаком, равно работе силы упругости. Теперь формулу для вычисления работы силы упругости можно озвучить по-другому: работа силы упругости равна изменению потенциальной энергии упруго деформированного тела (пружины), взятому с обратным знаком:

Работа силы упругости, как и работа силы тяжести, зависит только от начального и конечного положения центра груза – это означает, что работа силы упругости не зависит от формы траектории груза, а в том случае, когда траектория является замкнутой, работа силы упругости равна 0.

Если за начало отсчета принять положение груза при недеформированной пружине, а после принять, что удлинение пружины равно  (см. рис. 7), то формула для работы силы упругости приобретает вид:

Рис. 7. Вычисление работы силы упругости

Но  – это потенциальная энергия пружины при ее удлинении на величину , следовательно, потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна 0.

Когда мы описывали потенциальную энергию тела, поднятого над землей, мы говорили, что потенциальная энергия – это энергия взаимодействия тел и в том случае это была энергия взаимодействия двух тел – груза и земли. Что касается силы упругости, то о ней можно сказать почти то же самое – это тоже энергия взаимодействия, однако теперь это энергия взаимодействия не различных тел, а частей одного и того же тела – в нашем случае это энергия взаимодействия частей пружины.

Теперь рассмотрим задачу.

Задача

Динамометр, рассчитанный на 40 Н, имеет пружину жесткостью 500 . Какую работу нужно совершить, чтобы растянуть пружину от середины шкалы до последнего деления?

Решение задачи

В условии нам не дано значений удлинения пружины динамометра, поэтому введем его сами. Пусть удлинение пружины на середине шкалы равно  (см. рис. 8).

Рис. 8. Удлинение шкалы

Следовательно, когда пружина растянута с максимальной силой, то удлинение равно . Воспользуемся для последнего случая законом Гука, поскольку мы знаем значение максимальной силы и жесткости пружины.

Откуда:

Следовательно, нам необходимо рассчитать работу при удлинении от 4 см до 8 см. Воспользуемся формулой, полученной на уроке:

Работа равна разности между значениями потенциальной энергии пружины, растянутой до полного удлинения и до полвины.

Ответ:.

Теперь мы с вами можем рассчитывать потенциальную энергию тела, поднятого над землей, и потенциальную энергию тела, которое испытывает упругую деформацию.

Список литературы

1. Соколович Ю. А., Богданова Г. С. Физика: справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
2. Перышкин А. В. Физика: учебник 10 класс. – Издательство: Дрофа.: 2010. – 192 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «fizika.in» (Источник)     
2. Интернет-портал Единой коллекции цифровых образовательных ресурсов (Источник)
3. Интернет-портал объединения учителей физики Санкт-Петербурга (Источник)

Домашнее задание

1. Что такое сила упругости?
2. Напишите формулу, по которой можно найти работу силы упругости.
3. Что такое потенциальная энергия тела?

---