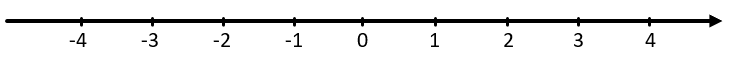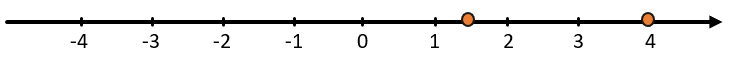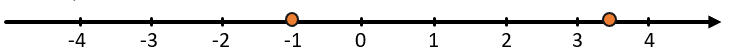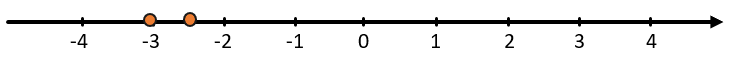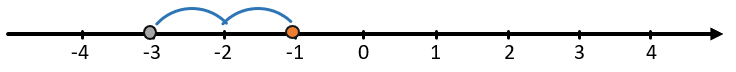Как найти рациональное число 9 класс

The method to represent and work with numbers is known as the number system. A number system is a system of writing to represent numbers. It is the mathematical notation used to represent numbers of a given set by using digits or other symbols. It has arithmetic operations to perform division, multiplication, addition, and subtraction between numbers. Some important number systems are as follows:

• Decimal Number System
• Binary Number System
• Octal Number System
• Hexadecimal Number System

Numbers and Digits 

Numbers are the counts or measurements used in mathematics, numerals are used to define numbers. A numeral can be defined as a symbol used for counting, for instance, there are 55 books in the library, where 56 is the numeral which is a combination of digits 5 and 6. A digit is a single numeral, the combination of digits form numerals. In the decimal number system, there are 10 digits, they are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

What are Naturals Numbers?

In the Number system, Natural numbers are the numbers that start from 1 and count up to Infinity. For example – (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16, 17, 18, 19, 20, 21..…….. ∞) are Natural Numbers.

What are Rational Numbers?  

A rational number is a number that can be represented in a p/q form such that q is not equal to 0. The set of rational numbers Include positive, negative numbers, and zero and it is denoted by Q. Rational number can also be expressed as a fraction.

When a number is expressed in a p/q form or in fraction form where both the numerator and the denominator part are integers, then the number is known as a rational number.  

Some examples of rational numbers are: 1/2, -2/7, 7/10, -7/10, 14/99

The number “0” is also a rational number, as we can represent it in many forms such as 0/1, 0/2, 0/3, etc. But, 1/0, 2/0, 3/0, etc. are not rational numbers because they give us infinite values.

Note: Rational numbers can also be expressed in decimal form.  

Types of Rational Numbers

There are different types of rational numbers and they are:

• Natural Numbers: All natural numbers are rational numbers because they can be written as in p/q form. Like 2 can be expressed in 2/1 (p/q) form.

Example – 1, 2, 3, 4, 5 …. etc.

• Terminating Decimals: Rational numbers can also be expressed in decimal form because decimal numbers can be represented in p/q form. For example, 1.1 can be written as 1.1 = 11/10. Thus all terminating decimals are rational numbers.

Example – ( 0.45, 0.7120, 0.9778 etc. )

• Non-Terminating Decimals: Non-Terminating decimals having repeated numbers after the decimal point such as 0.2222….., 0,12121212…. are also rational numbers. Since 0.222… can be written as 1/2, therefore it is a rational number. 

Example – ( 0.22222….., 0.121212…..  etc. )

• Fractions: When a number is expressed in a p/q form or in fraction form where both the numerator and the denominator part are integers, then it is a rational number.  

Example – 3/4, 2/7, 7/10, -7/10, 14/99 (all of them are in p/q form) 

• Whole Numbers: All whole numbers are rational numbers because the whole numbers can be expressed in p/q fraction form. 

Example – 0 is a rational number because it can be written as a fin 0/1, 0/-2,… etc.

How to identify rational numbers?

There are some conditions to check whether a number is a rational number or not. They are:

1. Always it is represented in the p/q form, where q≠0. For example – 3/4 , 2/7,  7/10, -7/10, 0/1 etc.

2. A rational number can be further simplified and represented in decimal form. For example – 0.9, -0.875, 3.25, -2.0 etc.

Sample Questions

Question 1. Is 2.2 is a rational number?

Answer:

Yes 2.2 is a rational number because 2.2 can also be written as p/q form that is 22/10.  

Question 2. Identify whether Mixed Fraction 1 5/4 is a Rational Number or Not?

Answer:

The Simplest Form of Mixed fraction 1 5/4 is 9/4. It is in p/q form. Thus, 9/4 is a Rational Number.

Question 3. How to Identify a Rational Number?

Answer: 

When a number is expressed in the p/q form where p, q are integers and q is non-zero then it called as a Rational Number.

Question 4. Is 12 a Rational Number?

Answer:

Yes 13 is a Rational Number because it can be expressed in 12/1 that is p/q form.

Question 5. Is 0 a rational number?

Answer:

Yes, 0 is a rational number because it is an integer and It can be written in p/q form such as 0/1, 0/2, where b is a non-zero integer. Hence, 0 is a rational number.

Question 6. Is 1 a Rational Number?

Answer:

Yes, 1 is a Rational Number because it can be expressed in 1/1 that is p/q form.

Question 7. Which of the following rational numbers are positive?

(i) (-4)/3         (ii) 9/8          (iii) (-14)/(-9)       (iv) (-21)/13

Answer:

9/8 is the only positive rational number.

смешанные числовые значения: [2 frac{1}{2}, 1 frac{2}{3},-2 frac{1}{3}]

• бесконечная периодическая дробь: например 0,(6) и т.п.

Пример 1. Целое числовое значение равное 2 может выражаться как в дробь [frac{2}{1}]

Следовательно, число 2, будет относиться к категории, не только целых чисел, но рациональных.

Пример 2. Смешанное значение равное [2 frac{1}{2}] можно преобразовать в дробь равную [frac{5}{2}]

Данное значение получается переводом смешанного значения в обычную неправильную дробь:

[ 2 frac{1}{2}=frac{(2 times 2)+1}{2}=frac{4+1}{2}=frac{5}{2} ]

Следовательно число:

Смешанное число [2 frac{1}{2}] можно отнести к рациональному числу.

Пример 3. Значение десятичной дроби,  у которой  значение равно 0,2 можно  преобразовать и выразить, как [frac{2}{10}].

Данное значение получилась переводом десятичного значения равного 0,2 в обычную обыкновенную дробь.

Данную дробь 0,2 можно записать как значение в виде [frac{2}{10}] из этого следует, что тогда она будет относиться к категории рациональных значений.

Пример 4. Периодическую бесконечную дробь, со значением равным 0, (3) можно представить как дробь вида: [frac{3}{9}]

Значение дроби получается при помощи перевода дроби периодического вида в дробь обыкновенного типа. Заданную бесконечную  периодическую дробь 0, (3) можно выразить как [frac{3}{9}] и тем самым отнести к категории рациональных чисел.

Расположение рациональных числовых значений на координатной прямой плоскости

Координатная прямая — это некая линия на плоскости, на которой расположено множество числовых значений. Имеет она следующий вид:

На вышеприведенном рисунке приведен фрагмент координатной прямой от значений −5 до 5.

Немного иначе обстоят дела с остальными категориями значений:

• обычные дробные значения;
•  числа смешанного типа;
•  десятичные дробные значения.

Данные значения расположены между целыми числами и данных значений множество.

Пример 1. Нужно определить на координатной прямой рациональное числовое значение  . Число располагается между значениями 1 и 2

Дробное значение равное [frac{3}{2}] можно записать как десятичную дробь равную 1,5. При увеличении участка координатной прямой от 1 до 2, можно увидеть следующую ситуацию:

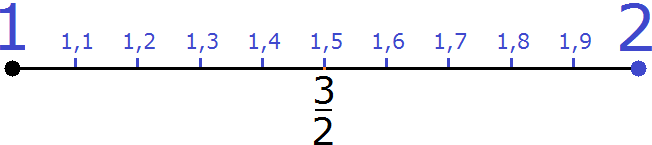
Между целыми значениями 1 и 2 находятся уже другие значения, которые являются десятичными дробями. Здесь же расположена дробь , которая находится  там же, где и дробь равная 1,5.

Увеличивая указанные отрезки на координатной прямой, можно увидеть остальные значения, которые лежат на данном отрезке.

В результате, можно обнаружить десятичные дроби, которые расположены после знака запятой одно значение.

Между значениями десятичных дробей, у которых после знака запятой имеют одну цифру, могут находится и другие десятичные дроби. В свою очередь они имеют после запятой два значения. Иными словами, сотые значения на отрезке.

Определим числа, которые находятся между десятичными значениями равными 0,1 и 0,2.

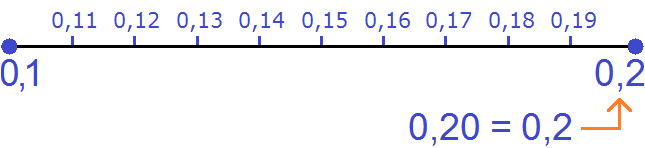
Пример 2. Необходимо определить на координатной прямой рациональное числовое значение.

Данное значение будет находиться ближе к нулевому значению.

Числовое значение дроби [frac{1}{50}] равно десятичной дроби 0,02

При увеличении отрезка от 0 до 0,1 можно определить, где расположено рациональное значение равное [frac{1}{50}]

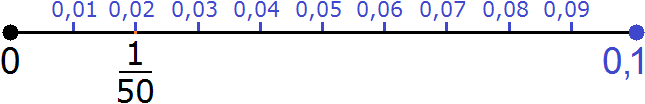
Пользуясь рисунком координатной прямой, можно сделать вывод:

Пользуясь рисунком координатной прямой, можно сделать вывод: [frac{1}{50}] расположено, там же , где и десятичная дробь равная 0,02.

Пример 3. Обозначим на прямой рациональное значение равное 0, (3).

Рациональное значение равное 0, (3) будет являться бесконечной периодической дробью.

Так как его дробное значение не заканчивается, оно бесконечное

0,33333…..

У значения периодической дроби 0,(3) дробная часть будет бесконечной, это значит, что: определить ее точное месторасположение на координатной прямой не представляется возможным. Данное место можно указать лишь частично.

Значение десятичной дроби равное 0,33333… будет расположено ближе к простой десятичной дроби значения 0,3.

На рисунке, нельзя точно увидеть месторасположение значения 0,(3).

Отрицательное значение перед рациональным числом

Рассмотрим простой пример:

(−6) : 2 = −3

В данном примере делимое равно  (−6)  и является отрицательным значением.

Далее можно рассмотреть иной пример. Составим и запишем выражение:

6 : (−2) = −3

В данном примере отрицательным является делитель равный (−2). Однако в двух случаях, при решении примеров, получается одинаковый ответ, который равен (−3). Данные примеры, также, можно записать в виде дробных значений.

Вид данных значений следующий [frac{-6}{2}=-3,-frac{6}{-2}=-3].

Так как в обоих случаях ответ, полученный при вычислении дробей, будет равным, то отрицательный знак, стоящий в числителе или в знаменателе можно вынести как общий. И тем самым, поставить его перед дробью:

[ frac{-6}{2}=-frac{6}{2}=-3,frac{6}{-2}=-frac{6}{2}=-3 ]

Следовательно между дробями и [frac{6}{-2}] и [-frac{6}{2}] есть возможность поставить равенство, так как они имеют одинаковое значение [frac{-6}{2}=frac{6}{-2}=-frac{6}{2}]

Противоположные значения рациональных чисел

По аналогии с простыми действительными числами, рациональное также может быть противоположным числом. 

Например: для рационального дробного значения равного [frac{1}{2}] противоположным числом будет значение дроби [-frac{1}{2}].

Данная дробь будет располагаться на координатной прямой в асимметричном расположении относительно дроби [frac{1}{2}] и начала координат. Иными словами, оба дробных значения удалены от нулевого значения (начала координат) на одинаковом расстоянии.

На нижеприведенном рисунке это можно увидеть досконально.

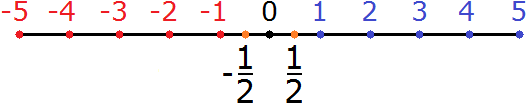
Основы перевода смешанных числовых значений в неправильную дробь

Для того чтобы осуществить перевод из смешанного числа в неправильную дробь, необходимо целую часть дроби перемножить со знаменателем дробной части и сложить полученное значение с числителем дробной части.

Вычисленное, будет являться числителем нового дробного значения. Следовательно, знаменатель остается прежним значением.

Пример 1. Необходимо перевести смешанное число равное [2 frac{1}{2}] в дробь неправильного вида. Для этого перемножим целую часть на значение знаменателя дробной части. Затем суммируем полученное значение к числителю дроби.

(2 × 2) + 1

Определим значение данного выражения:

(2 × 2) + 1 = 4 + 1 = 5 Вычисленное значение, которое равно 5 будет являться числителем нового

дробного значения. Значение знаменателя останется прежним [frac{5}{2}] Весь процесс проведения расчета можно записать в следующем виде, при помощи выражения:

[ 2 frac{1}{2}=frac{(2 times 2)+1}{2}=frac{4+1}{2}=frac{5}{2} ]

Чтобы преобразовать в первоначальный вид, нужно обозначить

целую часть дроби [frac{5}{2}] и получим [frac{5}{2}=2 frac{1}{2}].

Данный способ перевода из смешанного значения в неправильный дробный вид, применяется в ситуациях, когда смешанное число имеет положительное значение. Отрицательному числу данный способ, не подходит.

Для этого рассмотрим следующую дробь: [-frac{5}{2}]. Определим и выделим в данной дроби целую часть и получим следующее:

[ -2 frac{1}{2}. text { То есть }-frac{5}{2}=-2 frac{1}{2} text {. } ]

Для преобразования дроби в первоначальный вид [-frac{5}{2}] необходимо преобразовать смешанное число равное [-2 frac{1}{2}] в неправильную дробь.

Однако, если воспользоваться предыдущим правилом. Которое подразумевает умножение целой части на цифру знаменателя дроби и к полученному значению прибавить числитель дроби, то получается противоречие:

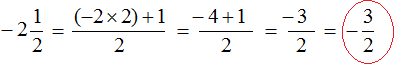
При вычислении данных получен ответ равный [-frac{3}{2}], а правильный ответ должен быть равен [-frac{5}{2}].

Выходит, что смешанное число значения [-2 frac{1}{2}] в неправильную дробь приведено неверно.

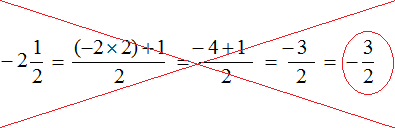
Для правильного решения необходимо перевести отрицательное число в неправильную дробь.

Для этого необходимо целую часть значения перемножить на числитель дроби.

Данное решение будет правильным, и ответ получится верным.

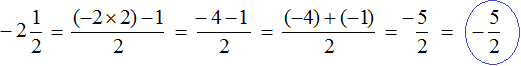
Пример 2. Нужно выделить в значении неправильной дроби [-frac{27}{5}] целую часть. Полученное число, смешанного значения преобразовать и перевести в неправильную дробь.

Применяя известные методы и правила выделим целую часть в заданном значении дроби [-frac{27}{5}]. Для данной дроби она будет равна: [-frac{27}{5}=-5 frac{2}{5}]

Далее полученный результат смешанного числа [-5 frac{2}{5}], необходимо перевести в дробь неправильного вида.

Для этого необходимо перемножить целую часть дроби на знаменатель. Из полученного значения необходимо отнять значение числителя дробной части:

[ -5 frac{2}{5}=frac{(-5 times 5)-2}{5}=frac{-25-2}{5}=frac{(-25)+(-2)}{5}=-frac{27}{5} ]

Для этого можно смешанное число переместить в скобки, отрицательный знак при этом расположить за скобками. Затем можно воспользоваться, уже известным правилом преобразования. А именно: умножить значение целой части на знаменатель данной дроби.  Далее к полученному значению прибавить числитель.

Выполним расчет данным способом, а именно, перевод смешанного число, которое равно [-5 frac{2}{5}] в неправильную дробь.

[ -5 frac{2}{5}=-left(5 frac{2}{5}right)=-left(frac{5 times 5+2}{5}right)=-left(frac{25+2}{5}right)=-left(frac{27}{5}right)=-frac{27}{5} ]

Рациональные числа и действия с ними

Рациональные числа – это числа, представленные в виде отношения (frac{m}{n}), где m – целое число, а n – натуральное.

Они могут быть как положительными, так и отрицательными.

Целые и дробные числа вместе образуют множество рациональных.

1. Любое целое число является рациональным, потому что его можно записать в виде (frac{m}{1}).

Например:

(–4 = frac{- 4}{1})

(2 = frac{2}{1})

(0 = frac{0}{1})

1. Сумма, разность и произведение двух рациональных чисел – тоже рациональное число. Частное двух рациональных чисел тоже будет рациональным, если знаменатель не равен 0.

2. Любое рациональное число можно записать в виде десятичной или периодической дроби.

Периодическая дробь – это десятичная дробь, в записи которой бесконечное количество раз повторяется цифра или несколько цифр.

Например:

(frac{1}{3} = 0,33333333..)

Повторяющиеся цифры периодической дроби записывают в скобках, например:

(frac{1}{3} = 0,(3))

(frac{5}{11} = 0,45454545 = 0,(45))

СВОЙСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение:

1. Переместительное свойство:

(a + b = b + a)

1. Сочетательное свойство:

(a + (b + c) = (a + b) + c = (a + c) + b = a + b + c)

1. Прибавление нуля не меняет рациональное число, а сумма противоположных чисел равна нулю:

(a + 0 = a)

(a + ( — a) = 0)

Умножение:

1. Переместительное свойство:

(ab = ba)

1. Сочетательное свойство:

(a(bc) = (ab)c = (ac)b = abc)

1. Умножение на единицу не меняет рациональное число, а произведение обратных чисел равно единице:

(a bullet 1 = a)

(a bullet frac{1}{a} = 1)

1. Если один из множителей равен нулю, то и всё произведение равно 0:

(a bullet 0 = 0)

(0 bullet b = 0)

(0 bullet 0 = 0)

1. Распределительное свойство:

((a + b)c = ac + сb)

ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ

Так как рациональные числа включают в себя блок целых чисел и блок дробных чисел, действия, пройденные в рамках работы с целыми числами, сохраняются и для рациональных чисел. Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.

СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Рациональные числа можно представить на координатной прямой, где справа от нуля находятся положительные числа, а слева от нуля – обратные им, отрицательные:

Числа на такой числовой прямой возрастают слева на право, поэтому глядя на прямую можно сказать, какое числе больше.

Например:

1. Сравним числа 1,5 и 4:

Мы знаем, что 4 больше, чем 1,5 и еще раз убедились в этом с помощью числовой прямой.

(4 > 1,5)

1. Сравним числа 3,5 и -1:

Если положительные числа справа от нуля, а отрицательные слева, тогда любое положительное числа будет правее отрицательного, а значит будет больше.

(3,5 > — 1)

1. Сравним числа -2,5 и -3:

Конечно, 3 больше 2,5, но, когда мы смотрим на отрицательные числа, получается, что -2,5 правее -3, а значит больше.

(- 2,5 > — 3)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение рациональных чисел так же можно представить на числовой прямой. Знак «+» означает, что мы двигаемся в положительном направлении (вправо), знак «–» означает, что мы двигаемся в отрицательном направлении (влево).

Например:

1. Найдем сумму положительных чисел 1 + 2,5. Значит от координаты 1 пройдем 2 полных отрезка и ещё половину отрезка в положительном направлении:

Видим, что (1 + 2,5 = 3,5).

Сумма положительных чисел – положительное число.

1. Найдем сумму отрицательных чисел -1 + (-2). От координаты -1 пройдем 2 отрезка в отрицательном направлении. При сложении можно опустить знак «+» без изменения знаков слагаемых.

Получилось, что (- 1 + ( — 2) = — 3.)

Сумма отрицательных чисел – отрицательное число.

1. Найдем разность положительных чисел 4 – 1,5. Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:

Получилось, что (4 –1,5 = 2,5.)

Сумма положительного и отрицательного числа – положительное число, если из большего вычитают меньшее.

1. Найдем сумму 2 + (-4). От координаты 2пройдем 4 отрезка в отрицательном направлении:

Получим, что (2–4 = — 2.)

Сумма положительного и отрицательного числа – отрицательное число, если из меньшего вычитают большее.

1. Найдем разность 1 – (-3). Если нужно пройти в отрицательном направлении дважды, то направление движения станет положительным, то есть 1 – (-3) = 1 + 3:

Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.

1. Найдем сумму двух противоположных чисел 3 + (-3). От координаты 3 пройдем 3 отрезка в отрицательном направлении:

Видим, что (3 + ( — 3) = 0.)

Сумма двух противоположных чисел (mathbf{= 0.})

УМНОЖНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

1. Рациональные числа умножаются и делятся не смотря на знак.

2. Если перемножались или делились числа с одинаковыми знаками, то в результате получается положительное число. Если перемножались числа с разными знаками, то в результате получается отрицательное число.

Например:

(3 bullet 4 = 12)

(- 6 bullet ( — frac{1}{2}) = 3)

(7:( — 2) = — 3,5)

(- 12:frac{1}{3} = — 12 bullet 3 = — 36)

Содержание:

• Определение рационального числа
• Операции над рациональными числами

Рациональные числа появились как форма записи чисел, более «мелких», нежели
натуральных.

Определение рационального числа

Если $m$ — нацело делится на $n$ или $n=1$, то рациональное число $frac{m}{n}$  также будет
целым числом; если при этом
$m$ будет натуральным, то в таком случае дробь $frac{m}{n}$  будет еще и натуральным числом. Поэтому для этих чисел имеет место такая цепочка вложений:
$N subset Z subset Q$ .

Операции над рациональными числами

На множестве рациональных можно ввести четыре арифметические операции:
сложение,
вычитание,
умножение и
деление; которые вычисляются по следующим правилам.

Правило вычисления суммы двух рациональных чисел:

$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$

Правило вычисления разности двух рациональных чисел:

$$frac{m}{n}-frac{p}{q}=frac{m cdot q-n cdot p}{n cdot q}$$

Правило вычисления произведения двух рациональных чисел:

$$frac{m}{n} cdot frac{p}{q}=frac{m cdot p}{n cdot q}$$

Правило вычисления частного двух рациональных чисел:

$$frac{m}{n} : frac{p}{q}=frac{m cdot q}{n cdot p}$$

Читать дальше: что такое сумма чисел.

Что такое рациональные числа

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы вновь поговорим о математических терминах.

И на этот раз расскажем все о РАЦИОНАЛЬНЫХ ЧИСЛАХ. Они обязательно входят в школьную программу, и дети начинают изучать их в 6 классе.

Само слово «рациональный» знакомо многим. И под ним подразумевается нечто «логичное» и «правильное». На деле так и есть.

Рациональные числа — это …

Термин имеет латинские корни, и в переводе «ratio» означает «число», «расчет», «разум», «рассуждение» и «нумерация». Но есть и другие переводы – «дробь» и «деление».

РАЦИОНАЛЬНОЕ ЧИСЛО – любое число, которое можно показать в виде дроби a/b. Здесь а – целое число, а b – натуральное.

Стоит напомнить, что:

1. Целые числа – это все возможные числа, как отрицательные, так и положительные. И к ним же относится ноль. Главное условие – они не должны быть дробными. То есть -15, 0 и +256 можно назвать целыми числами, а 2,5 или -3,78 – нет.
2. Натуральные числа – это числа, которые используются при счете, то есть они имеют «натуральное происхождение». Это ряд из 1, 2, 3, 4, 5 и так далее до бесконечности. А вот ноль и отрицательные числа, как и дробные – к натуральным не относятся.

И если применить эти определения, то мы можем сказать, что:

РАЦИОНАЛЬНОЕ ЧИСЛО – это вообще все возможные числа, кроме бесконечных непериодических десятичных дробей. Среди них натуральные и целые числа, обыкновенные и конечные десятичные дроби, а также бесконечные периодические дроби.

История изучения рациональных чисел

Точно неизвестно, когда люди начали изучать дроби. Есть мнение, что много тысяч лет назад. И началось все с банального дележа. Например, кому-то нужно было разделить добычу, но на равные части это не получалось сделать. Зато получалось сколько-то целых, и сколько-то в довесок.

Скорее всего, дроби изучали и в Древнем Египте, и в Древней Греции. Тогдашние математики далеко продвинулись в науке. И трудно предположить, что эта тема осталась ими не изучена. Хотя, к сожалению, ни в одних трудах так и не было найдено конкретных указаний на рациональные числа.

А вот официально считается, что понятие десятичной дроби появилось в Европе в 1585 году. Этот математический термин в своих трудах увековечил голландский инженер и математик Симон Стевин.

До занятия наукой, он был обыкновенным купцом. И скорее всего, именно в торговых делах часто сталкивался с дробными числами. Что потом и описал в своей книге «Десятая».

В ней Стевин не только объяснял полезность десятичных дробей, но и всячески пропагандировал их использование. Например, в системе мер для точного определения величины чего-либо.

Разновидности рациональных чисел

Мы уже написали, что под понятия рациональные числа подпадают практически все возможные варианты. Теперь рассмотрим более подробно существующие варианты:

1. Натуральные числа. Любое число с 1 и до бесконечности можно представить в виде дроби. Достаточно вспомнить простое математическое правило. Если поделить число на единицу, то получится то же самое число. Например, 5 = 5/1, 27 = 27/1, 136 = 136/1 и так далее.
2. Целые числа. Точно такая же логика, как в случае с натуральными числами, действует и тут. Отрицательные числа также можно представить в виде дроби с делением на единицу. И точно также будет в отношении нуля. Например, -356 = -356/1, -3 = -3/1, 0 = 0/1 и так далее.
3. Обыкновенные дроби. Это напрямую говорится в определении рациональных чисел. Например, 6/11, 2/5, -3/10 и так далее.
4. Бесконечные периодические дроби. Это числа, у которых после запятой бесконечное множество знаков и их последовательность повторяется. Самые простые примеры 1/3, 5/6 и так далее.
5. Конечные десятичные дроби. Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.

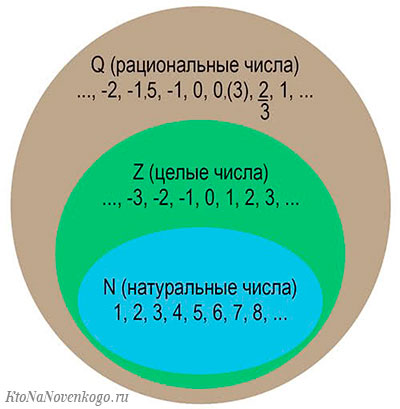
Все числа, которые входят в понятие рациональных, называются МНОЖЕСТВОМ рациональных чисел. В математике его принято обозначать латинской буквой Q.

А графически это можно изобразить вот так:

Свойства рациональных чисел

Рациональные числа подчиняются всем главным законам математики:

1. А + В = В + А
2. А + (В + С) = (А + В) + С
3. А + 0 = А
4. А + (-А) = 0
5. А * В = В * А
6. А * 1 = А
7. А * 0 = 0
8. (А + В) * С = А * С + В * С
9. (А – В) * С = А * С – В * С

Ради интереса можете попробовать подставить вместо букв любые числа и убедиться, что эти законы верны.

Вместо заключения

Раз есть в математике рациональные числа, значит, должны быть и им противоположные. Так и есть – они называются иррациональными. Это числа, которые нельзя записать в виде обычной дроби.

К таким числам относится математическая константа «пи». Многие знают, что она равна 3,14 и бесконечное количество знаков после запятой, причем их последовательность никогда не повторяется.

Также к иррациональным числам относится много корней. Это касается тех, у кого в результате не получается целого числа. Самый простой пример – корень из 2. Но это уже тема для другой статьи.