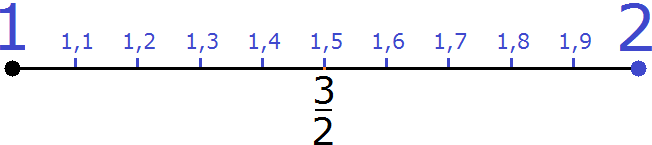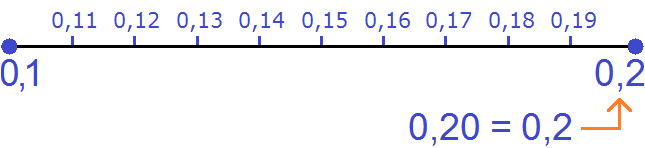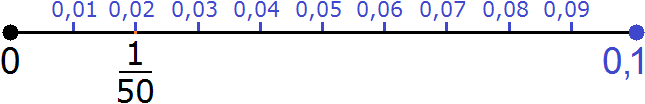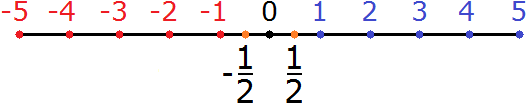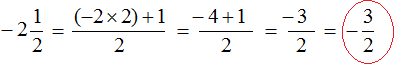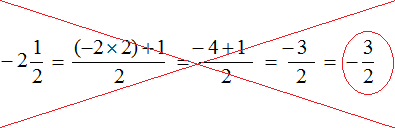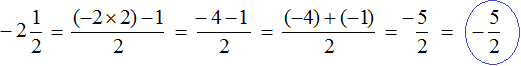Как найти рациональное число на отрезке - Исправление недочетов и поиск решений вместе с Examum.ru

Нужное рациональное число лежит на отрезке [√2 ; √3], поэтому оно положительное, а значит его можно представить как , где

Берём любое натуральное n, приводим границы двойного неравенства к общему знаменателю и вспоминаем, квадраты каких натуральных чисел лежат на нужном промежутке.

Получается дробь

Таким образом можно получить

Ответ: 1,5.

Источник

Мда… Ясно пока лишь то, что каша у меня в голове одна, да притом приличная. Сейчас попробую разобраться.

Рассмотрим интервал $b$ .

Не рассмотрим. Не удастся, т.к. число — ни разу не интервал.

А можем тогда рассмотреть интервал, допустим, $c$ с границами $x_1$ и $x_2$ () и сказать, что если для интервала найдётся некоторое число, скажем, $d$ внутри этого интервала, то для любого $c$ точка (это, кажется, следует из аксиом, описывающих операцию сложения и отношение порядка — пока не было времени глубже в этом разобраться)?

А дальше представляем, что , и тогда нам снова есть о чём говорить, как мне кажется.

Зорич в данном случае — не лучший вариант.

Однако исходить приходится из того, что как раз по Зоричу мы и идём (вернее, по конспекту, сделанному на его основе, иначе я бы раньше выполнил совет Hasek

Мы формулировали аксиому Архимеда так: «Множество натуральных чисел неограниченно».

Это бессмысленная формулировка. В том смысле, что оно не ограничено по самому своему определению. Выберите любую из вменяемых формулировок той аксиомы.

А вот тут сложно. И мой лектор, и Зорич формулируют эту аксиому как теорему и выводят из другой теоремы, теоремы о существовании точной верхней грани (лектор даёт ей название «принцип полноты Вейерштрасса»), которая, в свою очередь, выводится из аксиомы полноты, как вы и сказали, в варианте Дедекинда, разве что только в такой формулировке, что теория сечений не затрагивается. А дальше есть существенное различие: во-первых, Зорич выводит неограниченность натуральных чисел сверху, неограниченность целых чисел сверху и снизу, а потом формулирует принцип Архимеда так: «Если фиксировать произвольное положительное число $h$ , то для любого действительного числа $x$ найдётся и притом единственное целое число $k$ такое, что

Подход лектора отличается, он говорит, что сам принцип Архимеда заключается в том, что не ограничено сверху, а, как следствие, существует

И единственное, что мне пока непонятно, это почему вы считаете вторую формулировку бессмысленной. Я пытался думать в эту сторону, и, честно, не смог представить конечного индуктивного множества, и интуитивно я согласен, что смысла в этом особо нет. Впрочем, я уже вооружен знанием, что интуиция частно плохо срабатывает. Наверно, надо смотреть в сторону множеств, на которых не выполняются аксиома полноты и/или они неупорядочены, но для меня это пока слишком сложная материя. Возможно, всё станет яснее, когда я попытаюсь выводить нашу аксиому полноты как теорему, приняв, как сказал лектор, одновременно и принцип Архимеда, и принцип полноты Вейерштрасса за аксиому, но пока это тоже в сторону.

если аксиома Архимеда не выполняется

Не очень понятно, как именно вы хотите прийти к требуемому выводу. Несколько напоминает доказательство от противного, но там-то схема другая — если из отрицания вывода

следует отрицание посылки, то из посылки следует вывод, если я сколь-нибудь понятно изъясняюсь. Отрицать же посылку, как это делаете вы, бессмысленно — даже если вы выведете из этого отрицания чего интересного, решению задачи это ничем не поможет.

Наверно, я снова невнятно выразился… Вот увидел я аксиому в нашей формулировке: «Множество не ограничено сверху». И в задании сказано: «Доказать, используя аксиому Архимеда». Наверно, я должен предположить что-то, исходя из чего аксиома будет нарушена. Из чего она может быть нарушена? У нас есть следствие:

$n > frac{b}{a}$
Значит, если $frac{b}{a}$ не может превысить некоторого значения, то и $n$ не потребуется сколь угодно большим. Так я только пришёл к тому, откуда брать ограничение на $n$ .

Теперь ещё раз смотрю на задание: во всяком непустом интервале содержится рациональное число. Для начала я просто решил доказать, что в любом непустом интервале может быть какое-то число. А для этого уже взял интервал и стал показывать, что существуют такие $a < b$ , что (если бы таких $a$ не существовало, то нарушалась бы неограниченность сверху, что я и пытался показать в первой части первого сообщения). Так что, мне кажется, что отрицал я вывод и получил отрицание посылки (кстати, спасибо в этом месте: я раньше меньше задумывался над сутью метода «от противного»).

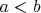
у меня есть процедура нахождения рационального числа между двумя другими рациональными

Само по себе это ещё не доказывает исходного утверждения. А что доказывает? Ну, например, если между двумя рациональными числами вы б научились вставлять много-много, и притом часто-часто…

Допустим, я умею вставлять их часто-часто. А как показать, что кого-то нельзя будет вставить настолько чаще, что между этими двумя «кем-то» не останется зазора для рационального числа? У меня получается только, что повторённое несколько раз постепенно становится истинным: для всякого $b$ можно найти меньшее число, так почему бы этому меньшему числу не быть рациональным… Наверно, отмету эту процедуру за ненадобностью, надо просто будет модифицировать первую часть так, чтобы найденное число имело вид $frac{m}{n}$ .

Источник

смешанные числовые значения: [2 frac{1}{2}, 1 frac{2}{3},-2 frac{1}{3}]

бесконечная периодическая дробь: например 0,(6) и т.п.

Пример 1. Целое числовое значение равное 2 может выражаться как в дробь [frac{2}{1}]

Следовательно, число 2, будет относиться к категории, не только целых чисел, но рациональных.

Пример 2. Смешанное значение равное [2 frac{1}{2}] можно преобразовать в дробь равную [frac{5}{2}]

Данное значение получается переводом смешанного значения в обычную неправильную дробь:

[
2 frac{1}{2}=frac{(2 times 2)+1}{2}=frac{4+1}{2}=frac{5}{2}
]

Следовательно число:

Смешанное число [2 frac{1}{2}] можно отнести к рациональному числу.

Пример 3. Значение десятичной дроби, у которой значение равно 0,2 можно преобразовать и выразить, как [frac{2}{10}].

Данное значение получилась переводом десятичного значения равного 0,2 в обычную обыкновенную дробь.

Данную дробь 0,2 можно записать как значение в виде [frac{2}{10}] из этого следует, что тогда она будет относиться к категории рациональных значений.

Пример 4. Периодическую бесконечную дробь, со значением равным 0, (3) можно представить как дробь вида: [frac{3}{9}]

Значение дроби получается при помощи перевода дроби периодического вида в дробь обыкновенного типа. Заданную бесконечную периодическую дробь 0, (3) можно выразить как [frac{3}{9}] и тем самым отнести к категории рациональных чисел.

Нет времени решать самому?

Наши эксперты помогут!

Расположение рациональных числовых значений на координатной прямой плоскости

Координатная прямая — это некая линия на плоскости, на которой расположено множество числовых значений. Имеет она следующий вид:

На вышеприведенном рисунке приведен фрагмент координатной прямой от значений −5 до 5.

Немного иначе обстоят дела с остальными категориями значений:

обычные дробные значения;
числа смешанного типа;
десятичные дробные значения.

Данные значения расположены между целыми числами и данных значений множество.

Пример 1. Нужно определить на координатной прямой рациональное числовое значение . Число располагается между значениями 1 и 2

Дробное значение равное [frac{3}{2}] можно записать как десятичную дробь равную 1,5.
При увеличении участка координатной прямой от 1 до 2, можно увидеть следующую ситуацию:

Между целыми значениями 1 и 2 находятся уже другие значения, которые являются десятичными дробями. Здесь же расположена дробь , которая находится там же, где и дробь равная 1,5.

Увеличивая указанные отрезки на координатной прямой, можно увидеть остальные значения, которые лежат на данном отрезке.

В результате, можно обнаружить десятичные дроби, которые расположены после знака запятой одно значение.

Между значениями десятичных дробей, у которых после знака запятой имеют одну цифру, могут находится и другие десятичные дроби. В свою очередь они имеют после запятой два значения. Иными словами, сотые значения на отрезке.

Определим числа, которые находятся между десятичными значениями равными 0,1 и 0,2.

Пример 2. Необходимо определить на координатной прямой рациональное числовое значение.

Данное значение будет находиться ближе к нулевому значению.

Числовое значение дроби [frac{1}{50}] равно десятичной дроби 0,02

При увеличении отрезка от 0 до 0,1 можно определить, где расположено рациональное значение равное [frac{1}{50}]

Пользуясь рисунком координатной прямой, можно сделать вывод:

Пользуясь рисунком координатной прямой, можно сделать вывод: [frac{1}{50}] расположено, там же , где и десятичная дробь равная 0,02.

Пример 3. Обозначим на прямой рациональное значение равное 0, (3).

Рациональное значение равное 0, (3) будет являться бесконечной периодической дробью.

Так как его дробное значение не заканчивается, оно бесконечное

0,33333…..

У значения периодической дроби 0,(3) дробная часть будет бесконечной, это значит, что: определить ее точное месторасположение на координатной прямой не представляется возможным. Данное место можно указать лишь частично.

Значение десятичной дроби равное 0,33333… будет расположено ближе к простой десятичной дроби значения 0,3.

На рисунке, нельзя точно увидеть месторасположение значения 0,(3).

Отрицательное значение перед рациональным числом

Рассмотрим простой пример:

(−6) : 2 = −3

В данном примере делимое равно (−6) и является отрицательным значением.

Далее можно рассмотреть иной пример. Составим и запишем выражение:

6 : (−2) = −3

В данном примере отрицательным является делитель равный (−2). Однако в двух случаях, при решении примеров, получается одинаковый ответ, который равен (−3). Данные примеры, также, можно записать в виде дробных значений.

Вид данных значений следующий [frac{-6}{2}=-3,-frac{6}{-2}=-3].

Так как в обоих случаях ответ, полученный при вычислении дробей, будет равным, то отрицательный знак, стоящий в числителе или в знаменателе можно вынести как общий. И тем самым, поставить его перед дробью:

[
frac{-6}{2}=-frac{6}{2}=-3,frac{6}{-2}=-frac{6}{2}=-3
]

Следовательно между дробями и [frac{6}{-2}] и [-frac{6}{2}] есть возможность поставить равенство, так как они имеют одинаковое значение [frac{-6}{2}=frac{6}{-2}=-frac{6}{2}]

Противоположные значения рациональных чисел

По аналогии с простыми действительными числами, рациональное также может быть противоположным числом.

Например: для рационального дробного значения равного [frac{1}{2}] противоположным числом будет значение дроби [-frac{1}{2}].

Данная дробь будет располагаться на координатной прямой в асимметричном расположении относительно дроби [frac{1}{2}] и начала координат.
Иными словами, оба дробных значения удалены от нулевого значения (начала координат) на одинаковом расстоянии.

На нижеприведенном рисунке это можно увидеть досконально.

Основы перевода смешанных числовых значений в неправильную дробь

Для того чтобы осуществить перевод из смешанного числа в неправильную дробь, необходимо целую часть дроби перемножить со знаменателем дробной части и сложить полученное значение с числителем дробной части.

Вычисленное, будет являться числителем нового дробного значения. Следовательно, знаменатель остается прежним значением.

Пример 1. Необходимо перевести смешанное число равное [2 frac{1}{2}] в дробь неправильного вида.
Для этого перемножим целую часть на значение знаменателя дробной части. Затем суммируем полученное значение к числителю дроби.

(2 × 2) + 1

Определим значение данного выражения:

(2 × 2) + 1 = 4 + 1 = 5 Вычисленное значение, которое равно 5 будет являться числителем нового

дробного значения. Значение знаменателя останется прежним [frac{5}{2}] Весь процесс проведения расчета можно записать в следующем виде, при помощи выражения:

[
2 frac{1}{2}=frac{(2 times 2)+1}{2}=frac{4+1}{2}=frac{5}{2}
]

Чтобы преобразовать в первоначальный вид, нужно обозначить

целую часть дроби [frac{5}{2}] и получим [frac{5}{2}=2 frac{1}{2}].

Данный способ перевода из смешанного значения в неправильный дробный вид, применяется в ситуациях, когда смешанное число имеет положительное значение. Отрицательному числу данный способ, не подходит.

Для этого рассмотрим следующую дробь: [-frac{5}{2}]. Определим и выделим в данной дроби целую часть и получим следующее:

[
-2 frac{1}{2}. text { То есть }-frac{5}{2}=-2 frac{1}{2} text {. }
]

Для преобразования дроби в первоначальный вид [-frac{5}{2}] необходимо преобразовать смешанное число равное [-2 frac{1}{2}] в неправильную дробь.

Однако, если воспользоваться предыдущим правилом. Которое подразумевает умножение целой части на цифру знаменателя дроби и к полученному значению прибавить числитель дроби, то получается противоречие:

При вычислении данных получен ответ равный [-frac{3}{2}], а правильный ответ должен быть равен [-frac{5}{2}].

Выходит, что смешанное число значения [-2 frac{1}{2}] в неправильную дробь приведено неверно.

Для правильного решения необходимо перевести отрицательное число в неправильную дробь.

Для этого необходимо целую часть значения перемножить на числитель дроби.

Данное решение будет правильным, и ответ получится верным.

Пример 2. Нужно выделить в значении неправильной дроби [-frac{27}{5}] целую часть. Полученное число, смешанного значения преобразовать и перевести в неправильную дробь.

Применяя известные методы и правила выделим целую часть в заданном значении дроби [-frac{27}{5}]. Для данной дроби она будет равна: [-frac{27}{5}=-5 frac{2}{5}]

Далее полученный результат смешанного числа [-5 frac{2}{5}], необходимо перевести в дробь неправильного вида.

Для этого необходимо перемножить целую часть дроби на знаменатель. Из полученного значения необходимо отнять значение числителя дробной части:

[
-5 frac{2}{5}=frac{(-5 times 5)-2}{5}=frac{-25-2}{5}=frac{(-25)+(-2)}{5}=-frac{27}{5}
]

Для этого можно смешанное число переместить в скобки, отрицательный знак при этом расположить за скобками. Затем можно воспользоваться, уже известным правилом преобразования. А именно: умножить значение целой части на знаменатель данной дроби. Далее к полученному значению прибавить числитель.

Выполним расчет данным способом, а именно, перевод смешанного число, которое равно [-5 frac{2}{5}] в неправильную дробь.

[
-5 frac{2}{5}=-left(5 frac{2}{5}right)=-left(frac{5 times 5+2}{5}right)=-left(frac{25+2}{5}right)=-left(frac{27}{5}right)=-frac{27}{5}
]

Источник

Математика

6 класс

Урок № 48

Изображение рациональных чисел на координатной оси

Перечень рассматриваемых вопросов:

Изображение рациональных чисел на координатной оси.
Определение длины отрезка по координатам его концов, заданных рациональными числами.
Определение координаты середины отрезка, концы которого заданы точками с рациональными координатами.
Среднее арифметическое чисел.

Тезаурус

Меньшее число на координатной оси лежит левее большего.

Точки, изображающие рациональные числа на координатной оси, называют рациональными точками или точками с рациональными координатами.

Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.

Список литературы

Обязательная литература:
Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Мы уже умеем изображать на координатной оси целые числа. Рациональные числа тоже можно изображать на координатной оси. Рассмотрим подробнее, как это делается.

Рациональному числу a на координатной оси соответствует точка, находящаяся на расстоянии модуля a от нуля влево, если a – отрицательное число, или вправо, если a – положительное число.

Эту точку называют точкой А, или точкой с координатой a.

Представим координатную ось. Чтобы изобразить на ней рациональное число, нужно сначала обозначить нулевую отметку и единичный отрезок.

Например, отметим на координатной оси число минус две третьих. Обозначим нулевую отметку и отметим единичный отрезок. Разделим единичный отрезок на три равные части. Количество частей соответствует знаменателю дроби, которую нам требуется изобразить.

Число отрицательное, значит, будет находиться слева от точки ноль на расстоянии, равном модулю минус двух третьих, т. е. на расстоянии двух третьих единичного отрезка. Отметим заданную точку.

Изобразим на координатной оси число три вторых, или одну целую одну вторую.

Число положительное, будет находиться справа от нуля. Отсчитаем вправо один единичный отрезок и ещё половину следующего. Это и будет искомая точка.

Если a и b рациональные числа, и a меньше b, то:

– точка a находится левее точки b на координатной оси:

– расстояние между точками a и b, или длина отрезка АB, равна разности координат b минус a;

– координата середины отрезка АB равна сумме координат a плюс b, разделённой на два.

a и b – рациональные числа, a < b

АB=b – a

Помните, что при обозначении единичного отрезка следует принимать во внимание знаменатель дроби, которую требуется изобразить на координатной оси. Единичный отрезок должен легко делиться на данный знаменатель, тогда отметить на оси рациональное число будет проще.