Как найти рациональные корни решение

10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ

Теорема 4. Если многочлен с целыми коэффициентами f (x) = a_nxⁿ + a_n-1x^n-1 + … + a₁x+a₀  имеет рациональный корень x=p/q (q ≠ 0, дробь p/q  несократимая), то р является делителем свободного члена (a₀), а q — делителем коэффициента при стар­шем члене а_n.

     Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем

an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0.

(1)

            Умножим обе части равенства (1) на  (q ≠ 0). Получаем

аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0.

(2)

В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому

a₀qⁿ = -(а_nрⁿ + a_n-1p^n-1q + … + a₁pq^n-1) делится на р.

Но когда мы записываем рациональное число в виде p/q, то эта дробь счи­тается несократимой, то есть р и q не имеют общих делителей. Произве­дение a₀qⁿ может делиться на р (если р и q — взаимно простые числа) только тогда, когда a₀ делится на р. Таким образом, р — делитель свобод­ного члена a₀.

Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда

a_npⁿ = -(a_n-1p^n-1q + … + a₁pq^-1 + a₀qⁿ) делится на q. Поскольку р и q — взаимно простые числа, то a_n делится на q, следовательно, q — де­литель коэффициента при старшем члене.

Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a₀. Таким образом, имеет место:

Следствие 1. Любой целый корень многочлена с целыми коэффи­циентами является делителем его свободного члена.

Если в заданном многочлене f (х) коэффициент а_n = 1, то делителями а_n могут быть только числа ±1, то есть q =±1, и имеет место:

Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.

Задача 1 Найдите рациональные корни многочлена 2х³ – х² + 12х – 6.

Пусть несократимая дробь p/q является корнем многочлена. Тогда р не­обходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.

Таким образом, рациональные корни многочлена необходимо искать сре­ди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.

Кроме того, по схеме Горнера мож­но записать, что

2х³ – х² + 12х – 6 = (x – 1/2) (2x² + 12).

Многочлен 2х² + 12 не имеет действительных корней (а тем более рацио­нальных), поэтому заданный многочлен имеет единственный рациональ­ный корень x =1/2.

Задача 2 Разложите многочлен Р (х) = 2х⁴ + 3х³ – 2х² – х – 2 на множители.

Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.

Тогда Р (х) = (х – 1)(2х3 + 5х² + 3х + 2). Ищем целые корни кубического многочлена 2х³ + 5х² + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2

Имеем  Р (х) = (х – 1)(х + 2)(2х² + х +1).

Квадратный трехчлен 2х² + х +1 не имеет действительных корней и на линейные множители не расклады­вается.

Ответ: Р (х) = (х – 1)(х + 2)(2х² + х +1).

Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х² + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры дока­зывается, что многочлен нечетной степени всегда можно разложить на ли­нейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.

Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого раз­ложения иногда можно применить метод неопределенных коэффициентов.

Задача 3 Разложите на множители многочлен х⁴ + х³ + 3х² + х + 6.

Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.

Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:

х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d),

(3)

где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Рас­кроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:

х⁴ + х³ + 3х² + х + 6 = x⁴ + cx³ + dx² +

                                                      + ax³ + acx² + adx +

                                                                    + bx² + bcx + bd.

Получаем систему

(4)

Попытка решить эту систему методом подстановки приводит к уравне­нию 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть толь­ко делителями числа 6. Все возможные варианты запишем в таблицу.

Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рас­сматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.

Для каждой пары значений b и d из третьего равенства системы (4) най­дем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.

Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид

x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3).

(5)

Поскольку квадратные трехчлены х² – х + 2 и х² + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.

Упражнения

1. Найдите целые корни многочлена:

1) х³ – 5х + 4;

2) 2x³ + x² – 13x + 6;

3) 5х³ + 18х² – 10х – 8;

4) 4х⁴ – 11х² + 9х – 2.

1. Найдите рациональные корни уравнения:

1) х³ – 3х² + 2 = 0;

2) 2х³ – 5х² – х + 1 = 0;

3) 3х⁴ + 5х³ – х² – 5х – 2 = 0;

4) 3х⁴ – 8х³ – 2х² + 7х – 2 = 0.

1. Разложите многочлен на множители:

1) 2х³ – х² – 5х – 2;

2) х³ + 9х² + 23х +15;

3) х⁴ – 2х³ + 2х – 1;

4) х⁴ – 2х³ – 24х² + 50х – 25.

1. Найдите действительные корни уравнения:

1) х³ + х² – 4х + 2 = 0;

2) х³ – 7х – 6 = 0;

3) 2х⁴ – 5х³ + 5х² – 2 = 0;

4) 2х³ – 5х² + 1 = 0.

5*. Разложите многочлен на множители методом неопределенных коэффи­циентов:

1) х⁴ + х³ – 5х² + 13х – 6;

2) х⁴ – 4х³ – 20х² + 13х – 2.

6*. Разложите многочлен на множители, заранее записав его с помощью ме­тода неопределенных коэффициентов в виде (х² + bх + с)² – (mх + n)²: :

1) х⁴+ 4х – 1;

2) х⁴ – 4х³ – 1;

3) х⁴ + 4а³х – а⁴.

Содержание:

1. Теорема о рациональных корнях
2. Задача пример №8
3. Задача пример №9
4. Задача пример №10

Теорема о рациональных корнях

Если для многочлена с целыми коэффициентами существует рациональный корень, то этот корень имеет вид

Доказательство:

Пусть несократимая дробь является корнем многочлена с целыми коэффициентами:

Умножим обе части равенства на :

Так как в последнем равенстве каждый член, кроме члена , содержит множитель и каждый член, кроме члена , содержит множитель , то коэффициент должен делится на , а коэффициент должен делится на .

Задача пример №8

Найдите рациональные корни многочлена .

Решение:

свободный член 6, старший коэффициент 2.

Для , запишем все возможные числа вида

, т.е. одним из множителей является двучлен . Другие множители найдем, используя синтетическое деление:

Так как, , получим, что являются корнями многочлена.

Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.

Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.

Задача пример №9

Найдите корни многочлена .

Решение:

по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.

Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.

Так как , то, решив квадратное уравнение , получим другие корни: . Значит данный многочлен третьей степени имеет три корня: —.

Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.

Например, для нахождения корней многочлена надо умножить все члены уравнения на 12, а затем решить полученное уравнение .

Для нахождения рациональных корней выполните следующие действия:

1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.

2. Из этих чисел выбирается число (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен , на который многочлен делится без остатка.

3. Для данного многочлена при помощи синтетического деления на двучлен определяется другой множитель.

4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.

5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена могут являться числа ±1.

Проверим: ; . Значит, многочленах не имеет рациональных корней.

Исследование:

1) Перепишите примеры в тетрадь и проведите обсуждение.

a) Многочлен первой степени имеет один корень:

b) Многочлен второй степени имеет два корня: , ;

c) Многочлен третьей степени имеет три корня:

d) Многочлен четвертой степени имеет четыре корня:

e) Принимая во внимание, что уравнение имеет кратные корни, получим 5 корней:

2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид .

3) Равна ли степень произвольного многочлена количеству его корней?

Покажем на примере, что многочлен n-ой степени имеет n корней.

Задача пример №10

Найдите все корни многочлена .

Решение:

рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

.

Значит, является корнем данного многочлена . Другие корни найдем синтетическим делением.

В выражении для множителя вновь применим теорему о рациональных корнях и синтетическое деление. Тогда ; . Решим уравнение ; ; (корень кратности 2); ;

Корни:

Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Теорема об остатке

Теорема о разложении на множители

Основная теорема алгебры

Функция-многочлен

Дробно-рациональные уравнения

Что такое дробно-рациональные уравнения

Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:

при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.

Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.

9 x 2 — 1 3 x = 0

1 2 x + x x + 1 = 1 2

6 x + 1 = x 2 — 5 x x + 1

Уравнения, которые не являются дробно-рациональными:

Как решаются дробно-рациональные уравнения

В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.

Алгоритм действий при стандартном способе решения:

1. Выписать и определить ОДЗ.
2. Найти общий знаменатель для дробей.
3. Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
4. Записать уравнение со скобками.
5. Раскрыть скобки для приведения подобных слагаемых.
6. Найти корни полученного уравнения.
7. Выполним проверку корней в соответствии с ОДЗ.
8. Записать ответ.

Пример 1

Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:

x x — 2 — 7 x + 2 = 8 x 2 — 4

Начать следует с области допустимых значений:

x 2 — 4 ≠ 0 ⇔ x ≠ ± 2

Воспользуемся правилом сокращенного умножения:

x 2 — 4 = ( x — 2 ) ( x + 2 )

В результате общим знаменателем дробей является:

Выполним умножение каждого из членов выражения на общий знаменатель:

x x — 2 — 7 x + 2 = 8 x 2 — 4

x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )

После сокращения избавимся от скобок и приведем подобные слагаемые:

x ( x + 2 ) — 7 ( x — 2 ) = 8

x 2 + 2 x — 7 x + 14 = 8

Осталось решить квадратное уравнение:

Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:

Примеры задач с ответами для 9 класса

Требуется решить дробно-рациональное уравнение:

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

Определим область допустимых значений:

О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2

x 2 + 7 x + 10 ≠ 0

D = 49 — 4 · 10 = 9

x 1 ≠ — 7 + 3 2 = — 2

x 2 ≠ — 7 — 3 2 = — 5

Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:

a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Сократим дроби, избавимся от скобок, приведем подобные слагаемые:

x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —

— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0

x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0

x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0

2 x 2 + 9 x — 5 = 0

Потребуется решить квадратное уравнение:

2 x 2 + 9 x — 5 = 0

Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.

Дано дробно-рациональное уравнение, корни которого требуется найти:

4 x — 2 — 3 x + 4 = 1

В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:

4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0

4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0

4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0

x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0

Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:

— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0

Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:

( x — 2 ) ( x + 4 ) ≠ 0

Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:

— x 2 — x + 30 = 0 _ _ _ · ( — 1 )

Получилось квадратное уравнение, которое можно решить:

Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.

Нужно решить дробно-рациональное уравнение:

x + 2 x 2 — 2 x — x x — 2 = 3 x

На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:

x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0

x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0

x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0

— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0

Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.

— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )

Корни квадратного уравнения:

x 1 = — 4 ; x 2 = 2

Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.

Найти корни уравнения:

x 2 — x — 6 x — 3 = x + 2

Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:

x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0

x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0

x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0

0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0

Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:

Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.

Ответ: х — любое число, за исключением 3.

Требуется вычислить корни дробно-рационального уравнения:

5 x — 2 — 3 x + 2 = 20 x 2 — 4

На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:

5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0

5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0

5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0

2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0

( x — 2 ) ( x + 2 ) ≠ 0

Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.

Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.

Ответ: корни отсутствуют

Нужно найти корни уравнения:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )

Начнем с определения ОДЗ:

— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0

При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )

( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )

( x — 3 ) x + x = x + 5

Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:

x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0

Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:

x 1 · x 2 = — 10 x 1 + x 2 = 3

В этом случае подходящими являются числа: -2 и 5.

Второе значение не соответствует области допустимых значений.

Рациональные уравнения с примерами решения

Содержание:

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Нахождение рациональных корней

Содержание:

Теорема о рациональных корнях

Если для многочлена с целыми коэффициентами существует рациональный корень, то этот корень имеет вид

Доказательство:

Пусть несократимая дробь является корнем многочлена с целыми коэффициентами:

Умножим обе части равенства на :

Так как в последнем равенстве каждый член, кроме члена , содержит множитель и каждый член, кроме члена , содержит множитель , то коэффициент должен делится на , а коэффициент должен делится на .

Задача пример №8

Найдите рациональные корни многочлена .

Решение:

свободный член 6, старший коэффициент 2.

Для , запишем все возможные числа вида

, т.е. одним из множителей является двучлен . Другие множители найдем, используя синтетическое деление:

Так как, , получим, что являются корнями многочлена.

Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.

Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.

Задача пример №9

Найдите корни многочлена .

Решение:

по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.

Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.

Так как , то, решив квадратное уравнение , получим другие корни: . Значит данный многочлен третьей степени имеет три корня: -.

Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.

Например, для нахождения корней многочлена надо умножить все члены уравнения на 12, а затем решить полученное уравнение .

Для нахождения рациональных корней выполните следующие действия:

1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.

2. Из этих чисел выбирается число (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен , на который многочлен делится без остатка.

3. Для данного многочлена при помощи синтетического деления на двучлен определяется другой множитель.

4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.

5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена могут являться числа ±1.

Проверим: ; . Значит, многочленах не имеет рациональных корней.

Исследование:

1) Перепишите примеры в тетрадь и проведите обсуждение.

a) Многочлен первой степени имеет один корень:

b) Многочлен второй степени имеет два корня: , ;

c) Многочлен третьей степени имеет три корня:

d) Многочлен четвертой степени имеет четыре корня:

e) Принимая во внимание, что уравнение имеет кратные корни, получим 5 корней:

2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид .

3) Равна ли степень произвольного многочлена количеству его корней?

Покажем на примере, что многочлен n-ой степени имеет n корней.

Задача пример №10

Найдите все корни многочлена .

Решение:

рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

.

Значит, является корнем данного многочлена . Другие корни найдем синтетическим делением.

В выражении для множителя вновь применим теорему о рациональных корнях и синтетическое деление. Тогда ; . Решим уравнение ; ; (корень кратности 2); ;

Корни:

Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Математика: полный курс решений задач в виде лекций

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Рациональные корни многочлена с целыми коэффициентами

Вопрос о нахождении
рациональных корней многочлена f(x)Q[x]
(с рациональными коэффициентами) сводится
к вопросу об отыскании рациональных
корней многочленов k
∙ f(x)Z[x]
(с целыми коэффициентами). Здесь число
k
является наименьшим общим кратным
знаменателей коэффициентов данного
многочлена.

Необходимые, но
не достаточные условия существования
рациональных корней многочлена с целыми
коэффициентами дает следующая теорема.

Теорема 6.1 (о
рациональных корнях многочлена с целыми
коэффициентами).
Если
–рациональный
корень многочлена f(x)
= a_n

xⁿ+
+
…+ a₁

x
+ a₀
с
целыми
коэффициентами,
причем (p,
q)
= 1, то числитель
дроби p
является делителем свободного члена
а₀,
а знаменатель q
является делителем старшего коэффициента
а₀.

Теорема
6.2. Если
Q
(где
(p,
q)
= 1)
является
рациональным корнем многочлена
f(x)
с целыми
коэффициентами, то
–целые
числа.

Пример. Найти
все рациональные
корни
многочлена

f(x)
= 6
x⁴
+ x³
+ 2
x²
–
4 х+
1.

1. По теореме 6.1:
если
–рациональный
корень многочлена f(x),
(где
(p,
q)
= 1), то
a₀
= 1

p,
a_n
= 6
q.
Поэтому p
{
1}, q{1,
2, 3, 6}, значит,

.

2. Известно, что
(следствие 5.3) число а
является корнем многочлена f(x)
тогда и только тогда, когда f(x)
делится на (х
– а).

Следовательно,
для проверки того, являются ли числа 1
и –1 корнями многочлена f(x)
можно воспользоваться схемой Горнера:

	6	1	2	– 4	1
1	6	7	9	5	6
– 1	6	– 5	7	–11	12

f(1)
= 60,f(–1)
= 120,
поэтому 1 и –1 не являются корнями
многочленаf(x).

3. Чтобы отсеять
часть оставшихся чисел
,
воспользуемся теоремой 6.2. Если выраженияилипринимает целые значения для соответствующих
значений числителяp
и знаменателя q,
то в соответствующих клетках таблицы
(см. ниже) будем писать букву “ц”, в
противном случае – “др”.

=	ц	ц	ц	др	др	др
=	ц	ц	ц	ц	др	др

4. С помощью схемы
Горнера проверяем, будут ли оставшиеся
после отсеивания числа
корнямиf(x).
Вначале разделим f(x)
на (х
–
).

	6	1	2	– 4	1
	6	4	4	–2	0

В результате
имеем: f(x)
= (х
–
)(6
x³
+ 4
x²
+
4 х
– 2) и
– кореньf(x).
Частное q(x)
= 6 x³
+ 4
x²
+
4 х
– 2 разделим
на (х
+
).

	6	1	2	– 4	1
–	6	–2	3	–5	3

Так
как q
(–)
= 30, то (–) не является корнем многочленаq(x),
а значит и многочлена f(x).

Наконец,
разделим многочлен q(x)
= 6 x³
+ 4
x²
+
+ 4 х
– 2 на (х
–
).

	6	1	2	– 4	1
	6	3	3	–3	0

Получили:
q
()
= 0, т.е.– кореньq(x),
а значит,
– кореньf
(x).
Таким образом, многочлен f
(x)
имеет два рациональных корня:
и.

Освобождение от алгебраической иррациональности в знаменателе дроби

В школьном курсе
при решении некоторых типов задач на
освобождение от иррациональности в
знаменателе дроби достаточно домножить
числитель и знаменатель дроби на число
сопряженное знаменателю.

Примеры. 1.
t
=
.

Здесь в знаменателе
срабатывает формула сокращенного
умножения (разность квадратов), что
позволяет освободиться от иррациональности
в знаменателе.

2. Освободиться от
иррациональности в знаменателе дроби

t
=

. Выражение
– неполный квадрат разности чисела
=
иb
= 1. Воспользовавшись формулой сокращенного
умножения а³
– b³=
(а
+ b)
· (a²
– ab
+ b²),
можно определить множитель m
= (а + b)
=
+ 1, на который следует домножать числитель
и знаменатель дробиt,
чтобы избавиться от иррациональности
в знаменателе дроби t.
Таким образом,

t
=
.

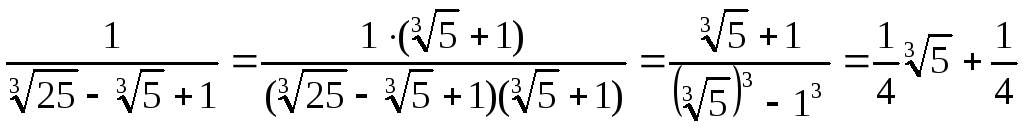
В ситуациях, где
формулы сокращенного умножения не
работают, можно использовать другие
приемы. Ниже будет сформулирована
теорема, доказательство которой, в
частности, позволяет найти алгоритм
освобождения от иррациональности в
знаменателе дроби в более сложных
ситуациях.

Определение 6.1.
Число z
называется алгебраическим
над полем
F,
если существует многочлен f(x)
F[x],
корнем которого является z,
в противном случае число z
называется трансцендентным
над полем F.

Определение 6.2.
Степенью
алгебраического над полем
F
числа
z
называется степень неприводимого над
полем F
многочлена p(x)F[x],
корнем которого является число z.

Пример. Покажем,
что число z
=
является алгебраическим над полемQ
и найдем его
степень.

Найдем неприводимый
над полем Q
многочлен p(х),
корнем которого является x
=
.
Возведем обе части равенстваx
=
в
четвертую степень, получимх⁴
= 2 или х⁴
– 2
= 0. Итак, p(х)
= х⁴
– 2, а степень
числа z
равна deg
p(х)
= 4.

Теорема 6.3
(об освобождении
от алгебраической иррациональности в
знаменателе дроби). Пусть
z
– алгебраическое число над полем F
степени n.
Выражение вида t
=
,где
f(x),
(x)F[x],
(z)0

единственным
образом может быть представлено в виде:

t
= с_n-1
z^n-1
+ c_n-2
z^n-2
+ … + c₁
z
+ c₀,
c_i

F.

Алгоритм освобождения
от иррациональности в знаменателе дроби
продемонстрируем на конкретном примере.

Пример.
Освободиться от иррациональности в
знаменателе дроби:

t
=

1. Знаменателем
дроби является значение многочлена
(х)
= х²
– х
+1 при х
=
.
В предыдущем примере показано, что– алгебраическое число над полемQ
степени 4, так как оно является корнем
неприводимого над Q
многочлена p(х)
= х⁴
– 2.

2. Найдем линейное
разложение НОД ((х),
p(x))
с помощью алгоритма Евклида.

_
x⁴

– 2 |
x²
– x
+ 1

x⁴–
x³+
x²


x²
+ x = q₁(x)

_
x³–
x²
–
2

x³–
x²+
x

x²
– x
+ 1 |
– x
–2 = r₁
(x)

x²
+ 2x

– x +
3
= q₂(x)

_–3x
+
1

–3x
– 6

_
– x
–2 |7
= r₂

– x
–2
—x
—
=q₃(x)

0

Итак, НОД ((х),
p(x))
= r₂
=
7. Найдем
его линейное разложение.

Запишем
последовательность Евклида, пользуясь
обозначениями многочленов.

p(x)
=
(x)
· q₁(x)
+ r₁(x)
r₁(x)
=
p(x)
–
(x)
· q₁(x)

(x)
= r₁(x)
· q₂(x)
+ r₂(x)
r₂(x)
=
(x)
– r₁(x)
· q₂(x)

r₁(x)
= r₂(x)
· q₂(x).

Подставим в
равенство 7= r₂(x)
=
(x)
– r₁(x)
· q₂(x)
значение остатка r₁(x)
= p(x)
–
(x)
· q₁(x),
после преобразований получим линейное
разложение НОД((х),
p(x)):
7 = p(x)
· (– q₂(x))
+
(x)
· [1 + q₁(x)
· q₂(x)].
Если подставить в последнее равенство
вместо обозначений соответствующие
многочлены и учесть, что p()
= 0, то имеем:

(1 –
+)
· (–+ 2+ 3+ 1)] = 7 (1)

3. Из равенства (1)
следует, что если знаменатель дроби t
умножить на число m
= [1 + (–
+ 2+ 3+ 1)], то получим 7. Таким образом,

t
=
=.

МЕТОДИКА 16.
Тема урока: Стандартный вид многочлена

Класс: 7

Тип урока: урок проверки и контроля
знаний и умений

Цели урока:

— проверить умения приводить многочлен
к стандартному виду

— развивать у учащихся логическое
мышление, внимание

— воспитывать самостоятельность

Структура урока:

1. Организационный момент

2. Инструктаж

3. Самостоятельная работа.

Задания:

1. Дополните предложения:

а) Выражение, содержащее сумму одночленов
называют …(многочленом).

б) Многочлен состоящий из стандартных
одночленов и не содержащий подобных
слагаемых называется … (стандартным
многочленом).

в) Наибольшую из степеней одночленов
входящих в многочлен стандартного вида
называют … (степенью многочлена).

г) Прежде чем определить степень
многочлена, нужно … (привести его к
стандартному виду).

д) Для нахождения значения многочлена
нужно сделать первое…(представить
многочлен в стандартном виде), второе
…(подставить значение переменной в
данное выражение).

2. Найти значение многочлена:

а) 2a⁴—ab+2b²приa=-1, b=-0,5

б) x²+2xy+y²приx=1,2, y=-1,2

3. Привести многочлен к стандартному
виду:

а) -5ах²
+ 7а²х + 2а²х +
9ах² – 4ах² –
8а²х;

б) (5х²
– 7х – 13) – (3х² – 8х + 17);

в) 2а
– (1,4ав + 2а² – 1) + (3а + 6,4ав);

г)
(2с² – 1,6с + 4) – ((10,6с²
+ 4,4с – 0,3) – (3,6с² – 7с –
0,7));

4.
Привести многочлен к стандартному виду
и выяснить при каких значениях хего значение равно 1:

а)
2x²-3x—x²-5+2x—x²+10;

б)
0,3x³—x²+x—x³+3x²+0,7x³-2x²+0,07

Билет
№ 17.
Делимость
целых чисел

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В уравнении такого типа a не равно 0, вместо b,c,d могут быть любые однозначные числа.

Данный вид уравнения имеет как минимум один корень – y₁.

Решение таких равнений может осуществляться разными способами. Оно может преобразовываться в стандартное квадратное уравнение. В таком случае предстоит выбрать один из трех вариантов решения квадратного уравнения:

• разложение на множители;
• применение формул для квадратных уравнений;
• метод дополнения.

Решение кубических уравнений может осуществляться посредством формулы Кардано, а также теоремы Виета. Теорема Виета применяется для решения последней, четвертой степени.

Решение кубических уравнений с двумя членами

Деление на a предполагает вместо нее любую цифру, кроме 0. После преобразования можно применить формулы для решения кубических уравнений, например, сокращенного умножения суммы кубов:

y3=b/a=0

(y+³√b/a)(y²—³√b/a*y+³√(b/a)²)=0

В результате из первой скобки выводим:

y=-³√b/a

во второй скобке получаем выражение – трехчлен:

y2-3√b/a*y+3√(b/a)2

Методы решения кубических уравнений возвратного вида

Первым делом при решении таких уравнений в математике выполняется группировка:

ay3+by2+by+a=a(y³+1)+b(y²+y)=a(y+1)(y²-y+1)+by(y+1)=(y+1)(ay²+y(b-a)+a)

В полученном выражении корень равен y=-1. Исходя из этого, чтобы получить корень квадратного трехчлена ay²+y(b-a)+a, потребуется найти дискриминант.

Решение кубических уравнений в составе которых рациональные корни

Предположим, что y=0. В этом случае он будет корнем уравнения, которое выглядит следующим образом:

ay³+by²+cy+d=0

При условии, что в уравнении свободные члены, d=0. Преобразуем уравнение и получим:

ay3+by2+cy=0

Решение кубических уравнений такого вида предполагает вынесение y за скобку. В итоге получается уравнение вида:

y(ay²+by+c)=0

Рассмотрим на конкретном примере, как решить кубическое уравнение с подробным решением:

5y³+2y²+4y=0

Решение:

Первым делом стоит упростить уравнение.

5y³+2y²+4y=0

Получим уравнение вида:

y(5y²+2y+4)=0

y=0, так как является корнем выражения.

Следующий шаг – поиск корней квадратного трехчлена 5y²+2y+4, который мы получили после упрощения. Для поиска приравняем к нулю и будем использовать дискриминант.

В ходе решения кубического уравнения с дискриминантом получим:

D=2²-2*5*4=-38

Так как в ответе мы получили отрицательное значение, корней у данного трехчлена нет, значит x=0.

Если в уравнениях вида ay³+by²+cy+d=0 коэффициентами являются целые числовые значения, то при решении таких уравнений и нахождении его значения мы может получить иррациональные корни.

В случае, когда a не равно 0, при умножении на a² каждой составляющей уравнения происходит замещение переменных, и получается: x=ay

ay³+by²+cy+d=0

Каждую составляющую выражения умножаем на a²:

a³*y³+b*a²*y²+c*a*a*y+d*a²=0

Учитывая, что решение кубических уравнений с подробным решением предполагает замещение переменных x=ay, то:

x²+b*x²+c*a*x+d*a²

Полученное уравнение является кубическим. В таких уравнениях корни могут быть разными – и целыми, и рациональными. Чтобы привести такое уравнение к тождественному равенству, потребуется подставить делители в полученное равенство. В этом случае полученный x₁ будет корнем, и в то же время корнем начального уравнения:

x₁=y₁/a

Чтобы найти значение корней квадратного трехчлена, потребуется многочлен ay3+by2+cy+d разделить на y-y_1.

Рассмотрим решение кубических уравнений такого вида на примере.

Пример:

Решить уравнение [x 3-3 x 2-13 x+15=0].

Решение:

Ищем первый корень перебором чисел: [0, pm1, pm2, pm3, pm5, pm15] и подстановкой в уравнение. В результате находим, что 1 является корнем. Тогда делим левую часть этого уравнения на двухчлен x-1 и получаем:

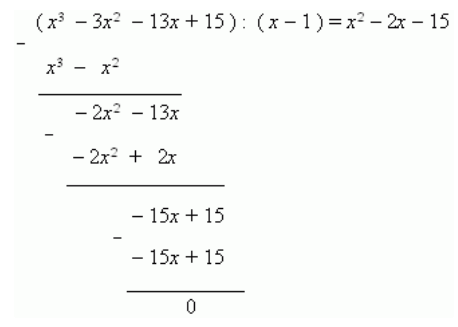
Теперь, решая квадратное уравнение: [x 2-2 x-15=0], находим оставшиеся два корня: x1=-3 и x2=5.

Ответ: 1; -3; 5.

Такой способ решения кубических уравнений используется для преобразования и решения возвратных уравнений. Из приведенного примера видно, что корнем является -1, значит, левую часть можно разделить на x+1. После того, как эти действия выполнены, можно находить корни квадратного трехчлена. Если рациональные корни отсутствуют, необходимо находить иные методы решения и разложения многочлена на множители.

Решение кубического уравнения с помощью формулы Кардано

Есть еще один способ — формула Кардано для решения кубических уравнений.

Если взять уравнение вида B₀y³+B₁y²+B₂y+B₃=0, то A₁=B₁/B₀, A₂=B₂/B₀, A₃=B₃/B₀.

Z=-A²₁/3+A₂

P=2A³₁/27-A₁A₂/3+A₃.

Выведенные значение Z и P подставим в формулу Кардано.

X=³√-P/2+√P²/4+Z³/27+³√-P/2-+√P2/4+Z3/27

В итоге подбор кубических корней должен соответствовать значению –Z/3. В этом случае корни исходного уравнения будут выглядеть следующим образом:

y=x-A₁/3

Применить формулу Кордано можно на примере для наглядности.

В данном случае для корней начального уравнения мы получим:

x₁=y₁-2=3-2=1;

x₂=y₂-2=-3-2=-5;

x₃=y₃-2=0-2=-2.

Получаем ответы: 1, -5, -2.

Общее решение кубического уравнения, если известен один из корней

За исходное уравнение возьмем следующее:

y³+ay²+by+c=0

Предположим, что a,b,c являются действительными цифровыми значениями. Известный корень пометим, как y₁. В таком случае, если произвести деление начального уравнения y³+ay²+by+c=0 на y-y₁ получим квадратное уравнение. При решении такого уравнения удастся найти еще два корня – y₂ и y₃.

Чтобы доказать это, преобразуем кубический многочлен следующим образом:

y₃+ay₂+by+c=(y-y₁)(y-y₂)(y-y₃)

При решении таких уравнений часто допускаются ошибки. Их решение – это сложное, многократное преобразование, которое требует точного знания формул и математических законов. Чтобы избежать ошибок и погрешностей, потребуется применить не только практические навыки, но и теоретические знания. Для решения кубических уравнений можно использовать специальный онлайн калькулятор. Принцип его действия основан на формуле Кардано. В том случае, если один или несколько коэффициентов такого уравнения равны нулю, или между ними присутствует определенная зависимость, решение будет более простым.

Чтобы научиться решать подобные уравнения, необходимо рассматривать примеры и тренироваться на их решении разными способами.