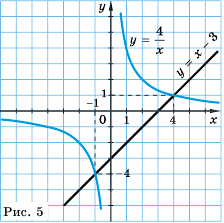
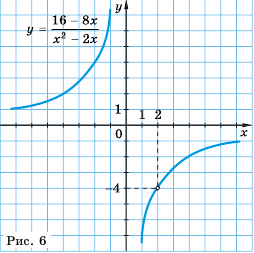
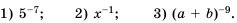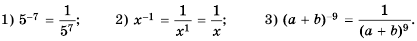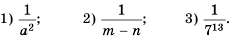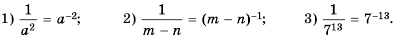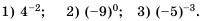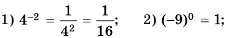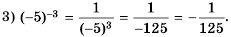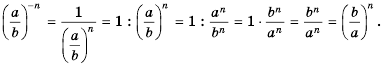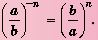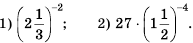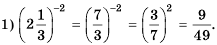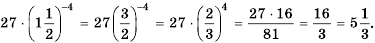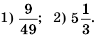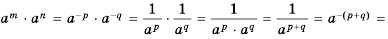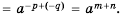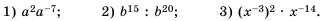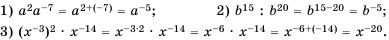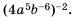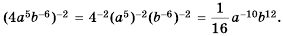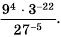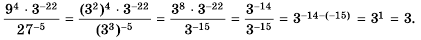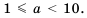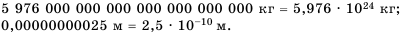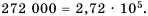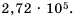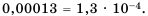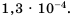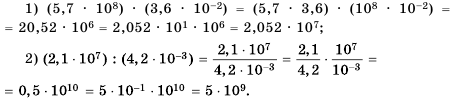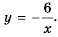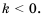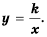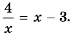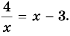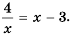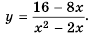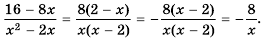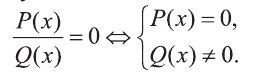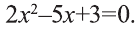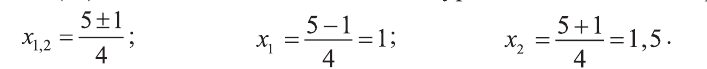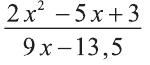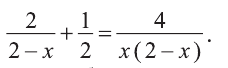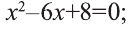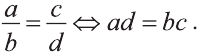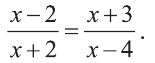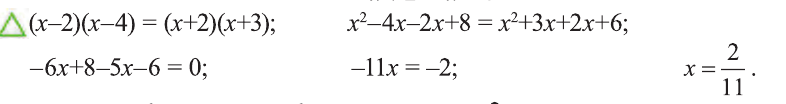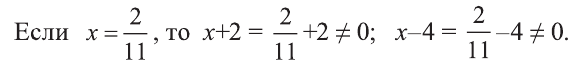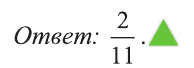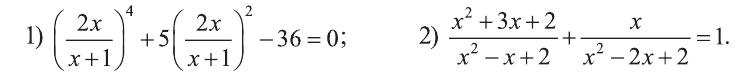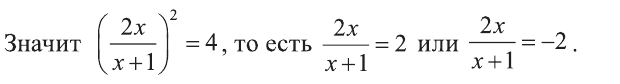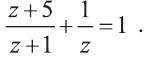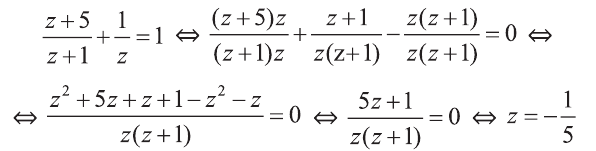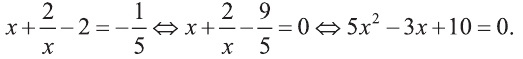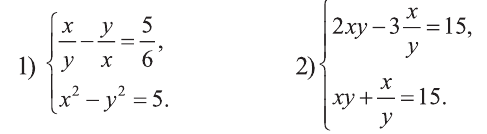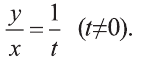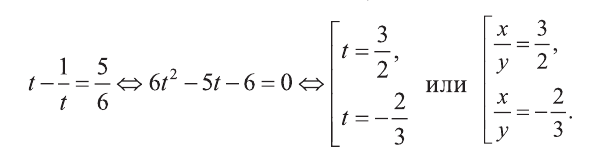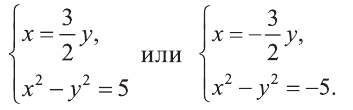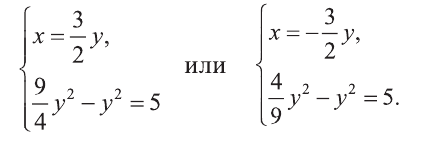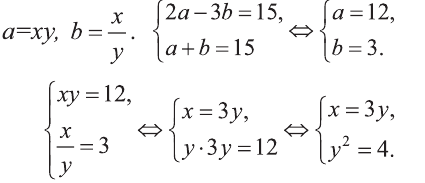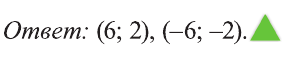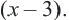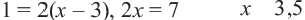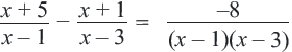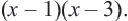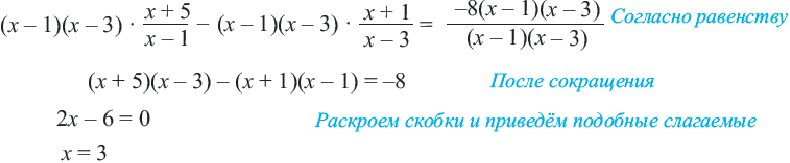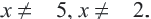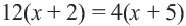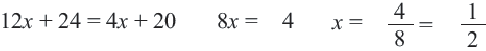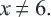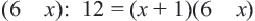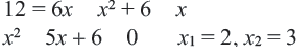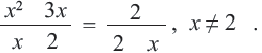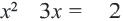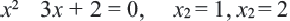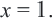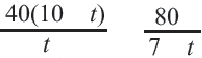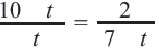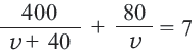Рациональные уравнения — алгоритмы и примеры вычислений
Общая информация
Рациональным уравнением называется равенство с одним или несколькими неизвестными, в правой и левой частях которого содержатся только рациональные выражения. Очень важно уметь определять тип, поскольку от этого зависит правильность нахождения корней и методика решения.
Определение можно немного упростить. Рациональным называется выражение, состоящее из некоторых числовых значений и неизвестной, операций вычитания, сложения, умножения, деления, а также возведения в степень с целым (натуральным) показателем. Уравнение рационального типа — равенство двух выражений, состоящих из переменных рационального типа (r (x) = 0). Они бывают двух видов: целые и дробные.
К первым относятся тождества, в знаменателе которых не содержится неизвестная величина. Примерами являются: x + 7 = 2x, x 2 + 2x — 7 = 0 и (x 2 + 4) / 2 = 2x / 4. Дробные представлены правильными дробями, числитель и знаменатель которых содержат переменные рационального типа. Примерами дробно-рациональных уравнений являются (x + 7) / 2x = 7 — x, (x 2 + 2x — 7) / (x 2 — 4) = 0 и (x 2 + 4) / 2x^ — 8 = 2x / 4.
Математики выделяют еще одну группу рациональных уравнений с параметрами, которые необходимо найти или они даются при решении задачи. Параметр — некоторое ограничение, влияющее на поиск корней.
Основные виды
Рациональные уравнения бывают линейными, квадратными, кубическими и биквадратными. Для каждого вида существуют определенные методики решения. Последние строятся на алгоритмах, позволяющих оптимизировать процесс нахождения корней.
Уравнения могут объединяться в системы. Чтобы ее решить, нужно найти все ее корни, удовлетворяющие ее элементам (выражениям). Отличаются равенства между собой только показателем степени. Например, у линейного последняя соответствует единице, у квадратного — 2, кубического — 3 и биквадратным — 4. Если в выражении с неизвестным присутствует дробная часть, всегда проверяется знаменатель на равенство нулю, поскольку такое значение превращает тождество в неопределенность. Числитель проверять нет необходимости. Выбор алгоритма решения рационального уравнения зависит от типа выражения.
Линейные и квадратные
Линейное выражение с неизвестными можно записать следующим образом: a1 * y1 + a2 * y2 +. + an * yn + c = 0. Например, 5х + 4 = 8 является линейным. Решается оно с помощью простого алгоритма:
- Необходимо перенести неизвестные величины в левую сторону, а известные — в правую: 5х = 8 — 4.
- Перенести число «5» с противоположным знаком: x = (8 — 4) / 5 = 4 / 5 = 0,8.
Квадратные уравнения — тождества вида az 2 + bz + c = 0. Они бывают полными (присутствуют все коэффициенты) и неполными. В последних какой-либо из параметров равен нулю. В зависимости от методики нахождения его корней, выбирается нужный алгоритм. Основные способы решения:
- Теорема Виета (при a = 1).
- Нахождение дискриминанта.
- Графический метод.
- Автоматизированный.
При использовании теоремы Виета значения корней вычисляется по таким формулам: z1 + z2 = — b и z1 * z2 = c. Если а > 1 (b и c не равны 0), то необходимо найти некоторый параметр. Математики называют его дискриминантом. Для решения существует специальный алгоритм:
- Выполнить расчет дискриминанта, и записать результат в виде квадрата: D = b 2 — 4ac.
- Если D больше 0, то два корня уравнения вычисляются таким образом: z1 = [(-b) + (D)^(½)] / (2 * а) и z2 = [(-b) — (D)^(½)] / (2 * а).
- При D = 0 две формулы во втором пункте преобразуются в одну, поскольку дискриминант не учитывается: z = [-b] / (2 * а). В этом случае существует только один корень.
- Когда при подсчете значения D получается отрицательное число, корней у уравнения нет вообще.
- После нахождения корней нужно подставить их в исходное выражение. Результат вычисления будет равен 0. Все остальные значения, приводящие к неверному тождеству, являются неверными. Их необходимо отсеивать. Это происходит, когда квадратное уравнение имеет вид обыкновенной дроби.
Следующим способом является графический метод решения. Для его реализации необходимо построить параболу, а затем найти точки пересечения с осью абсцисс (корни). Использование дополнительного программного обеспечения (онлайн-калькуляторов) для автоматизации вычислений экономит много времени. Его рекомендуется применять для проверки.
При отсутствии свободного члена (az^2 + bz = 0), можно воспользоваться методом разложения на множители. Для этого следует разделить обе части равенства на «а», а затем вынести общий множитель. В результате получится выражение z(z + b) = 0. У него два корня: z1 = 0 и z2 = -b.
Кубические тождества
Выражение вида а * z 3 + b * z 2 + с * z + d = 0 (а > 0), содержащее одну неизвестную, называется кубическим уравнением. Его метод решения зависит от вида. В алгебре выделяют 4 класса:
- az 3 + d= 0.
- az 3 + bz 2 + bz + a = 0.
- az 3 + bz 2 + cz = 0.
а * z 3 + b * z 2 + с * z + d = 0.
Первый класс решается просто. Для этого необходимо перенести свободный член d в правую часть, а затем разделить на «а»: z 3 = -d/a. После этого можно взять кубический корень из правой и левой частей. Кроме того, можно не переносить d, а просто разложить на множители: z 3 + d/a = (z + (d/a)^(1/3)) * (z 2 — [(d/a)^(1/3)]z + [(d/a)^2]^(1/3)) = 0. Разложив на множители, нужно решить 2 уравнения.
Чтобы решить второй тип задания, нужно выполнить некоторые математические преобразования: az 3 + bz 2 + bz + a = a (z 3 + 1) + b (z 2 + z) = a (z + 1)(z 2 — z + 1) + bz (z + 1) = (z + 1)(az 2 + z (b — a) + a) = 0. В результате этой операции произошло понижение степени. Далее нужно решить 2 равенства с неизвестными.
В третьем классе нужно просто вынести неизвестную (общий множитель) за скобку, а затем решить линейное и квадратное уравнения. Кроме того, этот тип тождеств решается также при помощи графического метода или замены переменной. Четвертый класс решается только с помощью построения графика (графическое представление — кубическая парабола) или заменой неизвестной.
В первом случае нужно построить кривую, которая называется кубической параболой. После этого следует найти точки пересечения графика с осью абсцисс. Метод замены — введение нового параметра, приводящего к равносильному упрощенному выражению. Сведение к квадратному многочлену осуществляется по такому алгоритму:
- Разделить обе части на «а».
- Выполнить замену: z = w — (b/(3a)).
- Вычислить коэффициенты р и q: p = [(3ас — b 2 ) / (3а 2 )] и q = [2b 3 — 9abc + (27a 2 ) * D] / (27a 3 ).
- Записать результат: w 2 + pw + q = 0.
- Решить квадратное уравнение.
- Вычислить z, подставив корни из пятого пункта во второй.
- Осуществить проверку.
Последний пункт также можно выполнить в автоматизированном режиме, поскольку это займет меньше времени. Методика позволяет избавиться от высшей степени и свести выражение к квадратному многочлену.
Биквадратные уравнения
Биквадратные уравнения (az 4 + bz 2 + c = 0) — сложные выражения. Они решаются аналитическим методом, который заключается в понижении степени. В этом случае вводится новая неизвестная для понижения степени w = z 2 . В результате этого получается равносильное равенство вида: aw 2 + bw + c = 0. Далее решается обыкновенное квадратное уравнение, а затем его корни подставляются в параметр замены.
Когда биквадратный многочлен с неизвестными представлен в виде az 4 + bz 3 + cz 2 + dz + e = 0, нужно решать при помощи формулы Кардана. Математики рекомендуют воспользоваться алгоритмом:
- Рассчитать вспомогательные коэффициенты: f = b / a, g = c / a и h = d / a.
- Вычисление основных параметров: i = -((f)^2 / 3) + g и k = [2 (f)^3 / 27] — [(f * g) / 3] + h.
- Нахождение по формуле Кардана математического ожидания: m = [(-k / 2) + ((k 2 / 4) + i 3 / 27)^(½)]^(1/3) + [(-k / 2) — (-(k 2 / 4) + i 3 / 27)^(½)]^(1/3).
- Поиск искомых корней: z1 = m — f, z2 = m — g и z3 = m — h.
Математическое ожидание — область, принимающая среднее значение при определенных условиях. Если уравнение имеет другой вид, корни следует искать с помощью математического ожидания Кардана. Однако его следует править в зависимости от коэффициентов исходного тождества. Можно также построить график функции, но эта методика довольно сложная.
Для этого специалисты рекомендуют пользоваться сторонними сервисами, одним из которых является «yotx.ru». Он позволяет строить разные графики. Особенностью веб-приложения является его гибкая настройка, а также табличные данные зависимости значения функции от ее аргумента, которыми можно воспользоваться. Полученный график можно распечатать, сохранить на жестком диске, получить в виде ссылки и html-кода для сайта или урока.
Пример решения
После получения теоретических знаний следует приступить к практике. Начинать следует с простых примеров, заканчивая более сложными. Например, выполнить работу по нахождению корней равенства с неизвестными: [(2z^3 — 16) / (2z^2 — 4z + 2)] = 0.
Уравнение является рациональным. Оно состоит из двух выражений: числителя и знаменателя. Первый следует приравнять к нулю, поскольку при делении на любое выражение будет получено нулевое значение. Однако не все так просто — нужно обязательно проверить знаменатель. Следует найти корень или корни, при которых он обращается в ноль, превращая все тождество в пустое множество или неопределенность. Чтобы найти корни числителя, нужно воспользоваться алгоритмом:
Рациональные уравнения с примерами решения
Содержание:
Рациональные уравнения. Равносильные уравнения
два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.
Так, например, равносильными будут уравнения
Уравнения 
Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.
1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;
2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Левая и правая части каждого из них являются рациональными выражениями.
Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.
В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.
Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.
Применение условия равенства дроби нулю
Напомним, что 
Пример №202
Решите уравнение
Решение:
С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду 


Окончательно получим уравнение:
Чтобы дробь 


Тогда 




Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:
Значит, решая дробное рациональное уравнение, можно:
1) с помощью тождественных преобразований привести уравнение к виду
2) приравнять числитель 
3) исключить из его корней те, при которых знаменатель 
Использование основного свойства пропорции
Если 

Пример №203
Решите уравнение
Решение:
Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то 


Сложив выражения в правой части уравнения, приведем его к виду: 
По основному свойству пропорции имеем:
Решим это уравнение:

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.
Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:
Таким образом, для решения дробного рационального уравнения можно:
1) найти область допустимых значений (ОДЗ) переменной в уравнении;
2) привести уравнение к виду
3) записать целое уравнение 
4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Решите уравнение
Решение:
Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:
Областью допустимых значений переменной будут те значения 



Умножим обе части уравнения на это выражение:
Получим: 



Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.
Следовательно, число 12 — единственный корень уравнения. Ответ. 12.
Решая дробное рациональное уравнение, можно:
3) умножить обе части уравнения на этот общий знаменатель;
4) решить полученное целое уравнение;
5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.
Пример №205
Являются ли равносильными уравнения
Решение:
Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.
Первое уравнение имеет единственный корень 

Степень с целым показателем
Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:
где 
В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: 
Рассмотрим степени числа 3 с показателями 
В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:
Число 




Нулевая степень отличного от нуля числа а равна единице, то есть 
Вернемся к строке со степенями числа 3, где слева от числа 




Приходим к следующему определению степени с целым отрицательным показателем:
если 
Основные сведения о решении дробно-рациональных уравнений
Определение основных понятий по теме
Рациональным выражением является такое выражение в алгебре, в состав которого включены числа и переменная х, а также операции сложения, вычитания, умножения, деления, возведения в степень с натуральным показателем. Если пара рациональных выражений объединены знаком равенства, то перед нами рациональное уравнение.
Дробно-рациональное уравнение представляет собой не имеющее знак корня рациональное уравнение, в котором обе части записаны в виде дробных выражений.
В дробно-рациональном уравнении имеется как минимум одна дробь, содержащая в знаменателе переменную.
Например, дробно-рациональными уравнениями являются:
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые нельзя отнести к дробно-рациональным:
Алгоритм решения дробно-рациональных уравнений
В процессе решения дробно-рациональных уравнений требуется правильно определить область допустимых значений (ОДЗ). Когда корни уравнения найдены, следует проверить их на соответствие ОДЗ и выяснить, какие являются допустимыми. В противном случае образуются посторонние решения, что автоматически делает ответ неверным.
Предусмотрен стандартный алгоритм действий для поиска корней дробно-рациональных уравнений:
- Выписать и определить ОДЗ.
- Вычислить общий знаменатель дробей.
- Найти произведение каждого члена уравнения и общего знаменателя. После чего следует сократить полученные дроби, чтобы избавиться от знаменателей.
- Записать уравнение со скобками.
- Раскрыть скобки и привести подобные слагаемые.
- Найти корни уравнения, которое получилось после раскрытия скобок.
- Сверить найденные корни с ОДЗ.
- Решения, которые успешно прошли проверку, записать в ответ.
Примеры решения задач
Требуется найти корни дробно-рационального уравнения:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Рассмотрим уравнение из условия задания:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Определим область допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся формулой сокращенного умножения:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x 2 — 4 = ( x — 2 ) ( x + 2 )
В таком случае, общим знаменателем является следующее выражение:
Согласно стандартной последовательности действий, найдем произведение каждого члена уравнения и ( x — 2 ) ( x + 2 ) : x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Затем следует привести подобные слагаемые:
Решениями получившегося квадратного уравнения являются следующие корни:
Сравним результат вычислений с ОДЗ. Зная, что x ≠ 2 , исключим первый корень, как посторонний. Запишем в ответ второй корень.
Для закрепления материала и знаний метода решения дробно-рациональных уравнений попробуем решить еще одно задание с объяснением действий. Подобные задачи нередко приходится решать на уроках алгебры в восьмом классе.
Решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Рассмотрим уравнение из условия задания:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Воспользуемся способом разложения квадратного трехчлена на множители:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
Преобразуем квадратный трехчлен x 2 + 7 x + 10 с учетом найденных x 1 и x 2 :
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
В результате общий знаменатель равен:
Умножим все части уравнения на общий знаменатель:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 — — ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
Выполним сокращение дробей:
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
Избавимся от скобок:
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
Приведем подобные слагаемые:
2 x 2 + 9 x — 5 = 0
Тогда получим корни уравнения:
Соотнесем решения с областью допустимых значений, которую определили ранее. Первый корень является посторонним, что выявлено с помощью контрольной проверки. По этой причине в ответ следует записать только второй корень.
Задания для самостоятельной работы
Найти корни уравнения:
x — 1 2 + 2 x 3 = 5 x 6
x — 1 2 + 2 x 3 = 5 x 6
3 x — 3 + 4 x 6 = 5 x 6
Требуется решить дробно-рациональное уравнение:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
x 2 — 3 x + x — 5 = x + 5
x 2 — 3 x — 10 = 0
Вычислить корни уравнения:
33 + x 2 9 — x 2 + 7 + x x — 3 = — 2 + 4 — x x + 3
33 + x 2 9 — x 2 + 7 + x x — 3 = — 2 + 4 — x x + 3
— 33 — x 2 + ( 7 + x ) · ( x + 3 ) = — 2 ( x 2 — 9 ) + ( 4 — x ) · ( x — 3 )
Согласно ОДЗ, первый вариант решения не подходит:
http://www.evkova.org/ratsionalnyie-uravneniya
http://wika.tutoronline.ru/algebra/class/8/osnovnye-svedeniya-o-reshenii-drobnoraczionalnyh-uravnenij
Целые рациональные уравнения
Важно знать, что рациональные уравнения в свою очередь тоже разные бывают.
Если в дроби нет деления на переменную (то есть на ( displaystyle x), ( displaystyle y) и т.д.), тогда рациональное уравнение будет называться целым (или линейным) уравнением, вот примеры:
( displaystyle begin{array}{l}frac{2x}{3}=13-frac{3x}{2};\4(2y-3)=y-9.end{array})
Умеешь такие решать? – конечно, умеешь, упрощаешь и находишь неизвестное, тема-то 5-ого или 6-ого класса.
Ну, рассмотрим первый из примеров на всякий случай и по порядочку. Все неизвестные переносим влево, все известные вправо:
( displaystyle frac{2x}{3}+frac{3x}{2}=13);
Какой наименьший общий знаменатель будет?
Правильно ( displaystyle 6)!
Чтоб к нему привести домножаем и числитель и знаменатель первого слагаемое на ( displaystyle 2), а второго на ( displaystyle 3), этого делать не запрещено, если и числитель и знаменатель дроби умножить на одно и то же значение, то дробь от этого не изменится, т.к. ее можно будет сократить на то же число.
А ( displaystyle 13) не трогаем, оно нам не мешает, имеем:
( displaystyle frac{4x}{6}+frac{9x}{6}=13)
( displaystyle frac{13x}{6}=13),
А теперь делим обе части на ( displaystyle 13):
( displaystyle begin{array}{l}frac{x}{6}=1\x=6end{array})
Тут все просто?
Поскольку уравнение целое, что мы уже определили, то и ограничений никаких нет, ( displaystyle 6), так ( displaystyle 6), ну можно для верности подставить этот ответ в исходное уравнение, получим ( displaystyle 0=0), значит все верно и ответ подходит (ты можешь пересчитать, а вообще должно сойтись).
Дробно-рациональные уравнения
А вот еще одно уравнение ( displaystyle frac{5}{x+1}+frac{4{x}-6}{(x+1)cdot (x+3)}=3).
Это уравнение целое? НЕТ!!! Тут есть деление на переменную ( displaystyle x), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.
Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.
Для начала найдем наименьший общий знаменатель, это будет ( displaystyle (x+1)cdot (x+3)).
Важный момент!
В предыдущем примере, где было целое уравнение мы не стали свободный член ( displaystyle 13) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель ( displaystyle (x+1)cdot (x+3)).
А это тебе не шутки, переменная в знаменателе!
Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!
Это надеюсь, ты запомнишь, но давай посмотрим что вышло:
( displaystyle frac{5(x+1)cdot (x+3)}{x+1}+frac{(4{x}-6)cdot (x+1)cdot (x+3)}{(x+1)cdot (x+3)}=3cdot (x+1)cdot (x+3)).
Что-то оно огромное получилось, надо все посокращать:
( displaystyle 5(x+3)+(4{x}-6)=3cdot (x+1)cdot (x+3)).
Раскроем скобки и приведем подобные члены:
( displaystyle begin{array}{l}9x+9=3{{x}^{2}}+12x+9\3{{x}^{2}}+3x=0.end{array})
Ну как, это уже попроще выглядит, чем в начале было?
Выносим за скобку общий множитель: ( displaystyle 3xcdot (x+1)=0)
У этого уравнения два решения, его левая сторона принимает нулевое значение при ( displaystyle x=0) и ( displaystyle x=-1).
Вроде бы все, ну ладно давайте напоследок подставим корни ( displaystyle x=0) и ( displaystyle x=-1) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим ( displaystyle 0), получается ( displaystyle 3=3) –нет претензий?
С ним все нормально. А теперь ( displaystyle -1), и тут же видим в знаменателе первого члена ( displaystyle -1+1)!
Но ведь это же будет ноль!
На ноль делить нельзя, это все знают, в чем же дело???
Дело в ОДЗ — Области Допустимых Значений!
(если забыл что это, повтори тему «ОДЗ — область допустимых значений»!)
Всякий раз когда ты видишь уравнение, где есть переменные (( displaystyle x,y) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс.
Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.
Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:
ОДЗ: ( displaystyle x+1ne 0) и ( displaystyle x+3ne 0) ( displaystyle Rightarrow xne -1) и ( displaystyle xne -3).
Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами ( displaystyle x=0) и ( displaystyle x=-1) мы смело исключаем ( displaystyle x=-1), т.к. он противоречит ОДЗ.
Значит, какой ответ будет у решенного уравнения?
В ответ стоит написать только один корень, ( displaystyle x=0).
Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.
Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,
ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!
Рациональные выражения, уравнения и дробно-рациональные уравнения
Повторим еще раз то, что прошил в предыдущих разделах, больше используя язык математики.
Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной ( displaystyle x) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Ну а рациональное уравнение – это равенство двух рациональных выражений.
Дробно-рациональные уравнения – рациональные (без знака корня) уравнения, в которых левая или правая части являются дробными выражениями.
Например:
( displaystyle frac{{{x}^{2}}-2{x}-3}{{x}-1}-frac{x+1}{{x}-3}={{x}^{2}}-1) (чаще всего мы встречаем именно дробно рациональные уравнения).
В общем случае при решении рациональных уравнений мы стремимся преобразовать его к виду: Произведение = «( displaystyle 0)» или Дробь = «( displaystyle 0)«, например:
( displaystyle frac{left( {x}-2 right)left( x+3 right)left( {{x}^{2}}+1 right)}{xcdot left( {x}-3 right)}=0).
Тогда мы сможем сказать, что любой из множителей числителя может быть равен нулю, но знаменатель при этом нулю не равен.
Для этого нам нужно сначала всё перенести в левую часть уравнения (не забываем при этом поменять знаки между слагаемыми: «( displaystyle +)» на «( displaystyle —)» и наоборот).
Затем мы обычно приводим все к общему знаменателю, и пишем систему:
( displaystyle left{ begin{array}{l}Числитель=0,\Знаменательne 0.end{array} right.)
Например:
( displaystyle begin{array}{l}frac{{x}-2}{{{x}^{2}}+2{x}-3}-frac{x+1}{{{x}^{2}}+5x+6}=frac{3}{x+3}Leftrightarrow \Leftrightarrow frac{{x}-2}{left( {x}-1 right)left( x+3 right)}-frac{x+1}{left( x+2 right)left( x+3 right)}-frac{3}{x+3}=0Leftrightarrow end{array})
( displaystyle Leftrightarrow frac{{{x}^{2}}-4-left( {{x}^{2}}-1 right)-3left( {{x}^{2}}+{x}-2 right)}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow frac{-3{{x}^{2}}-3x+3}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow )
( displaystyle Leftrightarrow left{ begin{array}{l}{{x}^{2}}+{x}-1=0\left( {x}-1 right)left( x+2 right)left( x+3 right)ne 0end{array} right.Leftrightarrow left{ begin{array}{l}left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}end{array} right.\xne 1\xne -2\xne -3end{array} right.Leftrightarrow left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}.end{array} right.)
Если знаменателя нет, или он является числом, – тем лучше, не придется решать неравенство.
Как бы то ни было, в ЕГЭ все рациональные выражения степени больше ( displaystyle 2) легко преобразуются в произведение более простых выражений при помощи либо перегруппировки, либо замены переменных (см. раздел «Разложение многочлена на множители»).
Содержание:
- Теорема о рациональных корнях
- Задача пример №8
- Задача пример №9
- Задача пример №10
Теорема о рациональных корнях
Если для многочлена 
Доказательство:
Пусть несократимая дробь 

Умножим обе части равенства на 
Так как в последнем равенстве каждый член, кроме члена 







Задача пример №8
Найдите рациональные корни многочлена 
Решение:
свободный член 6, старший коэффициент 2.
Для 



Так как, 


Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Задача пример №9
Найдите корни многочлена 
Решение:
по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 



Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 
Например, для нахождения корней многочлена 


Для нахождения рациональных корней выполните следующие действия:
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 

3. Для данного многочлена при помощи синтетического деления на двучлен 
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 
Проверим: 


Исследование:
1) Перепишите примеры в тетрадь и проведите обсуждение.
a) Многочлен первой степени 
b) Многочлен второй степени 


c) Многочлен третьей степени 
d) Многочлен четвертой степени 
e) Принимая во внимание, что уравнение 
2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид 
3) Равна ли степень произвольного многочлена количеству его корней?
Покажем на примере, что многочлен n-ой степени имеет n корней.
Задача пример №10
Найдите все корни многочлена 
Решение:
рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

Значит, 

В выражении 








Корни:
Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Свойства прямоугольного треугольника
- Частное решение дифференциального уравнения
- Интегрирование иррациональных функций
- Площадь поверхности. Интеграл по площади поверхности
- Формула Пуассона
- Найти производную функции
- Исследовать функцию на непрерывность: пример решения
- Преобразование графиков функций
- Полный дифференциал функции: пример решения
- Прямые и плоскости в пространстве
решить уравнение
5x−3x−3−2=−3x
.
Перенесём все слагаемые в левую часть
5x−3x−3−2+3x=0
.
Для этого пользуемся равенствами (F = G) и (F — G = 0), которые выражают одну и ту же зависимость между (F) и (G). На основании этого правила мы перенесли член
−3x
в левую часть уравнения, изменив при этом его знак.
Преобразуем левую часть уравнения:
5x−3(xx−3−2(x(x−3)1+3(x−3x=x⋅(5x−3)−2xx−3+3x−3xx−3=5×2−3x−2×2+6x+3x−9xx−3==3×2+6x−9xx−3=3×2+2x−3xx−3.
Получили:
3×2+2x−3xx−3=0
.
Напомним, когда дробь равна нулю:
ab=0
— тогда, и только тогда, когда сразу удовлетворены два условия:
1. числитель дроби равен нулю ((а = 0));
2. знаменатель дроби отличен от нуля:
b≠0
.
Приравниваем к нулю числитель дроби в левой части уравнения, получим:
3×2+2x−3=0;x2+2x−3=0;x1,2=−2±22−4⋅1⋅(−3)2=−2±4+122=−2±42;x1=−2+42=1;x2=−2−42=−3.
Выполним проверку второго указанного выше условия. Соотношение
b≠0
означает для уравнения, что
xx−3≠0→x≠0;x≠3
. Корни
x1=1;x2=−3
являются решениями уравнения, т. к. удовлетворяют поставленному условию.
Ответ: (1; -3).
Содержание:
Рациональные уравнения. Равносильные уравнения
Напомним что:
два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.
Так, например, равносильными будут уравнения
Уравнения 
Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.
1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;
2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Рассмотрим уравнения:
Левая и правая части каждого из них являются рациональными выражениями.
Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.
В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.
Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.
Применение условия равенства дроби нулю
Напомним, что 
Пример №202
Решите уравнение
Решение:
С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду 


Окончательно получим уравнение:
Чтобы дробь 


Тогда 




Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:
Ответ. 3.
Значит, решая дробное рациональное уравнение, можно:
1) с помощью тождественных преобразований привести уравнение к виду
2) приравнять числитель 
3) исключить из его корней те, при которых знаменатель 
Использование основного свойства пропорции
Если 

Пример №203
Решите уравнение
х — 1 х — 2
Решение:
Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то 


Сложив выражения в правой части уравнения, приведем его к виду: 
По основному свойству пропорции имеем:
Решим это уравнение:

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.
Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:
Ответ. 4.
Таким образом, для решения дробного рационального уравнения можно:
1) найти область допустимых значений (ОДЗ) переменной в уравнении;
2) привести уравнение к виду
3) записать целое уравнение 
4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Решите уравнение
Решение:
Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:
Областью допустимых значений переменной будут те значения 



Умножим обе части уравнения на это выражение:
Получим: 



Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.
Следовательно, число 12 — единственный корень уравнения. Ответ. 12.
Решая дробное рациональное уравнение, можно:
1) найти ОДЗ переменной в уравнении; & 2) найти простейший общий знаменатель дробей, входящий в уравнение;
3) умножить обе части уравнения на этот общий знаменатель;
4) решить полученное целое уравнение;
5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.
Пример №205
Являются ли равносильными уравнения
Решение:
Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.
Первое уравнение имеет единственный корень 

Ответ. Нет.
Степень с целым показателем
Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:
где 
В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: 
Рассмотрим степени числа 3 с показателями 
В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:
Число 




Нулевая степень отличного от нуля числа а равна единице, то есть 
Вернемся к строке со степенями числа 3, где слева от числа 




Приходим к следующему определению степени с целым отрицательным показателем:
если 
Пример №206
Замените степень дробью:
Решение:
По определению:
Пример №207
Замените дробь степенью с целым отрицательным показателем:
Решение:
Пример №208
Вычислите:
Решение:
Рассмотрим, как возвести дробь 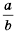
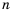
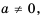
Следовательно,
Если 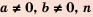
Пример №209
Найдите значение выражения:
Решение:
2) Учитывая порядок выполнения арифметических действий, сначала возведем дробь в степень, а затем выполним умножение:
Ответ.
Свойства степени с целым показателем
Свойства степени с натуральным показателем справедливы и для степени с ненулевым основанием и целым показателем. Следовательно,
Для любого 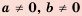
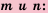
Эти свойства можно доказать на основании формулы 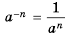
Докажем, например, формулу 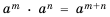
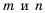
Пусть 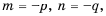
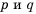
Следовательно, 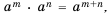
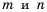
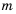
Пример №210
Выполните действие:
Решение:
Пример №211
Упростите выражение
Решение:
Пример №212
Вычислите
Решение:
Представим 9 и 27 в виде степени с основанием 3 и воспользуемся свойствами степени:
Ответ. 3.
Стандартный вид числа
В физике, химии, технике, астрономии часто имеют дело как с очень большими, так и с очень малыми значениями величин. Например, масса Земли равна 5 976 ООО ООО ООО ООО ООО ООО ООО кг, а диаметр молекулы водорода 0,00000000025 м.
Читать или записывать такие числа в виде десятичных дробей неудобно, неудобно и использовать десятичную их запись при вычислениях. В таких случаях имеет смысл записывать число в виде 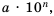
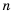
Например,
Говорят, что числа 5 976 000 000 000 000 000 000 000 и 0,00000000025 записаны в стандартном виде.
Стандартным видом числа называют его запись в виде произведении 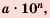
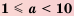
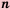
Если число записано в стандартном виде, то показатель степени 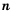
В стандартном виде можно записать любое положительное число. Порядок числа дает представление об этом числе.
Если порядок числа 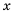
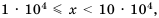
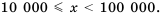
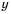
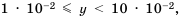
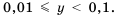
Следовательно, если говорят, что одно число на порядок больше второго, это означает, что оно в 10 раз больше второго, если на два порядка — в 100 раз больше и т. д.
Пример №213
Представьте число 272 000 в стандартном виде.
Решение:
В данном числе поставим занятую так, чтобы в целой части была одна цифра, отличная от нуля. В итоге будем иметь 2,72. Занятой отделили 5 цифр с конца числа, чем уменьшили данное число в 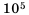
Ответ.
Пример №214
Представьте число 0,00013 в стандартном виде.
Решение:
В данном числе перенесем запятую на 4 знака вправо, будем иметь 1,3. При этом число увеличили в 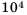
Ответ.
Пример №215
Выполните действия и представьте результат в стандартном виде:
Решение:
Ответ.
Пример №216
Найдите сумму 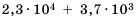
Решение:
Имеем два слагаемых разных порядков.
Ответ.
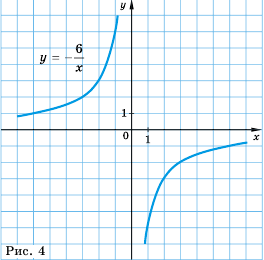
Функция Y=K/X ее график и свойства
Функция 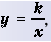
Пример №217
Пешеход должен преодолеть путь в 16 км. Если он будет двигаться со скоростью 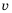
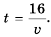
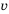
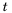
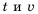
Пример №218
Площадь прямоугольника равна 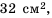
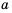
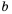
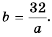
В примерах 1 и 2 переменные 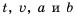
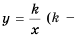
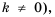
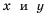
Функцию вида 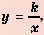
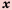
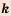
Область определения функции 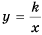
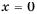

Построим график функции 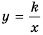
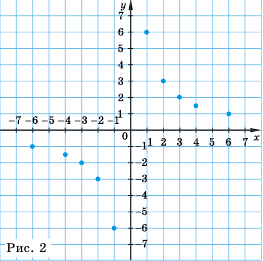
Пример №219
Постройте график функции
Решение:
Составим таблицу значений функции 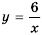
Отметим на координатной плоскости точки из составленной таблицы (рис. 2).
Если бы мы на этой плоскости обозначили больше точек, удовлетворяющих формуле 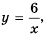
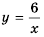
График обратной пропорциональности называют гиперболой.
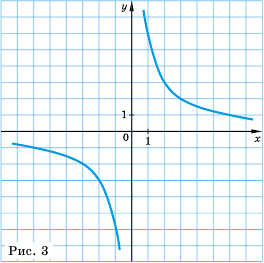
Гипербола состоит из двух ветвей. Для функции 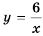
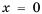
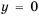
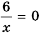
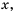
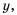
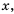
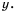
Так же выглядит график функции 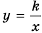
Пример №220
Постройте график функции
Решение:
Рассуждая как и в предыдущем примере, построим график функции 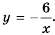
Это также гипербола, одна из ветвей которой лежит во второй координатной четверти, а другая — в четвертой.
Так же выглядит график функции 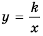
Обобщим свойства обратной пропорциональности
1. Область определения функции состоит из всех чисел за исключением нуля.
2. Область значений функции состоит из всех чисел за исключением нуля.
3. График функции — гипербола, ветви которой при 

4. Ветви гиперболы неограниченно приближаются к осям координат.
Пример №221
Постройте в одной системе координат графики функций 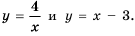
Решение:
График функции 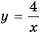
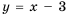
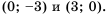
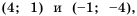
Действительно, при 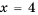
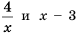
равные значения: 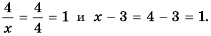
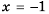
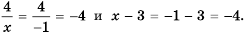
Ответ: 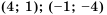
Предложенный в примере 5 метод решения уравнений называют графическим методом решения уравнений.
Если абсцисса точки пересечения графиков функций — целое число, надо выполнить проверку, т. к. часто корни уравнения этим методом можно найти только приблизительно.
Пример №222
Постройте график функции
Решение:
Область определения функции — все числа за исключением чисел 0 и 2, которые обращают знаменатель 
Упростим дробь:
Значит при условии 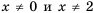
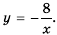
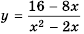
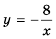
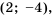
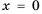
————
Если все решения одного уравнения также являются решениями второго, то второе уравнение называется следствием первого уравнения.
Если множества решений двух уравнений совпадают, то эти уравнения называются равносильными.
Пример 1.
Равносильны ли уравнения?
Решение:
1) Оба уравнения имеют общий корень: х=1. Так как они не имеют других корней, то они являются равносильными.
2) Первое уравнение имеет корень, равный 0. Второе же уравнение такого корня не имеет. Значит, данные уравнения не равносильны.
Пусть Р(х) и Q(x) — многочлены переменной х.
Выражение вида 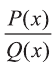
Пусть А(х) и В(х) — рациональные выражения. Уравнение вида А(х)=В(х) называется рациональным.
Рассмотрим сначала простейшее рациональное уравнение вида
Известно, что дробь 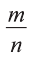
Для краткости, это мы будем записывать так:
- Заказать решение задач по высшей математике
Пример:
Решите уравнение:
Решение:
Уравнение 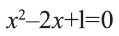
2) Квадратное уравнение 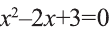
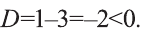
3) Для квадратного уравнения
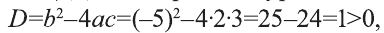
Однако число 1,5 обращает знаменатель выражения
в нуль, а число 1 — нет. Значит, данное уравнение имеет единственное решение х=1.
4) Уравнение 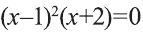
В случае, когда хотя бы одно из выражений А(х) и В(х) представимо в виде суммы нескольких рациональных выражений, рациональное уравнение А(х)=В(х) можно решить так:
- 1 шаг. Ищем общий знаменатель дробей, входящих в уравнение;
- 2 шаг. Обе части уравнения умножаем на этот общий знаменатель;
- 3 шаг. Ищем решения полученного уравнения;
- 4 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель в нуль.
Пример:
Решите уравнение
Решение:
Умножаем обе части уравнения на общий знаменатель 2х(2-х). Упрощая полученное уравнение 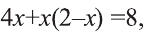
Так как D=9-8=l>0, то данное квадратное уравнение имеет два корня:
х=2; х=4.
Проверка.
При х=2 знаменатель обращается в нуль: х(2-х) = 2(2-2) = 0. Значит, х=2
не является решением исходного уравнения.
При х=4 знаменатель отличен от нуля х(2-х) = 4(2-4) Ф 0. Значит, х=4
является решением исходного уравнения.
Если 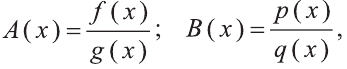
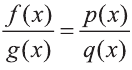
При этом получим следующий алгоритм решения:
- 1 шаг. Ищем решения уравнения f (х)q(х) = р(х)g(х)
- 2 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель q(x)g(x) в нуль.
Пример:
Решите уравнение
Решение:
В некоторых случаях удачно выполненная замена позволяет привести заданное уравнение к более простому.
Пример:
Решите уравнение:
Решение:
1) Выполним замену 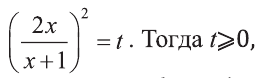
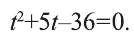
При 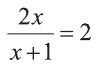
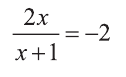
Ответ: х=-0,5.
2) Очевидно, что х=0 удовлетворяет уравнению. Пусть 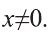
Тогда наше уравнение получит вид:
Решим последнее уравнение:
Теперь найдем x.
В силу того, что дискриминант квадратного уравнения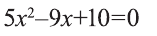
Системы рациональных уравнений
Решение систем, состоящих из рациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует не забывать, что знаменатели, участвующих рациональных выражений, не могут обращаться в нуль.
Пример:
Решите систему:
Решение:
1) Сделаем в первом уравнении замену 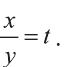
Отсюда или
Решим полученные системы:
Первая система имеет решения (3,2), (-3, -2), а вторая не имеет решений. Ответ: (3; 2), (-3; -2).
2). Обозначим
——
Рациональные уравнения
Рациональные уравнения широко применяются в приборостроении, космических исследованиях, финансовых операциях и т.д.
Подобие фигур широко применяется в измерительных, конструкторских и дизайнерских работах.
Это интересно!
На рисунке изображена модель орбитального космического корабля, предназначенная для полёта в космос туристов. Корабль рассчитан на 6 пассажиров и 2 членов экипажа.
Для того, чтобы рассчитать оптимальные размеры корабля конструкторам и инженерам пришлось решить много рациональных уравнений.
Рациональные уравнения
Уравнение, содержащее в левой и правой части рациональные выражения называется рациональным уравнением. Во многих задачах приходится решать рациональные уравнения, содержащие переменную в знаменателе. В этом случае необходимо указывать область допустимых значений переменных (ОДЗ).
Пример:
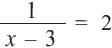
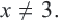
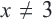
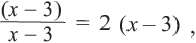
Подставим полученное значение в уравнение:
Таким образом, 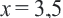
Пример:
Решим уравнение
ОДЗ данного уравнения 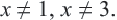
знаменатель
Пример:
В уравнении, 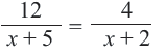
Используя свойство пропорции можно написать:
Пример:
Решим уравнение. 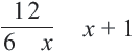
Умножим обе части уравнения на
Отсюда
Проверьте, являются ли оба этих числа корнями данного уравнения.
Пример:
Решим уравнение
Запишем уравнение в виде 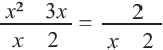
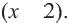
Отсюда
При проверке, убеждаемся что, 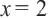
Внимание! После решения рационального уравнения, содержащего переменную в знаменателе, нужно обязательно выполнить проверку корней.
Решение задач с помощью рациональных уравнений
Задачи на работу
Задача. Двое рабочих могут выполнить некоторую работу за 12 дней. За сколько дней каждый рабочий выполнит эту работу в отдельности, если одному из них для выполнения этой работы потребуется на 10 дней больше ,чем другому? Решение: Пусть, 2-ой рабочий может выполнить работу за 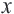
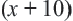
Первый рабочий за 1 день выполняет 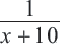
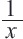
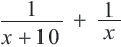
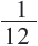
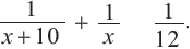
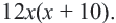
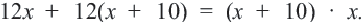


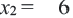

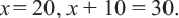
Задачи на движение
Задача. Путь длиной 480 км проходит по асфальтовой и по просёлочной дороге. Автомобиль расстояние 80 км по просёлочной дороге, прошёл со скоростью на 40 км/час меньше, чем по асфальтовой дороге. Зная, что на весь путь он затратил 7 часов, найдите время, которое потратил автомобиль при движении по просёлочной дороге.
1-й способ:
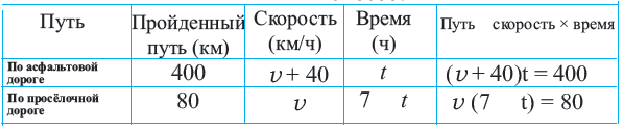
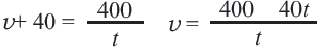
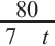
Разделим обе части уравнения на 40:
Получим 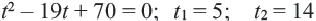
Ответ: по просёлочной дороге 2 часа
2-ой способ: Автомобиль ехал по дороге, покрытой асфальтом 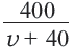
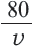
Зная, что на весь путь он потратил 7 часов, составим уравнение:
Решив данное уравнение, получим 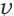
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Интеграл и его применение
- Параллельность в пространстве
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
- Множества