Как найти рад меру - Исправление недочетов и поиск решений вместе с Examum.ru

Алгебра и начала математического анализа, 10 класс

Урок №29. Радианная мера угла

Перечень вопросов, рассматриваемых в теме:

1) Понятие тригонометрической окружности;

2) Поворот точки вокруг начала координат;

3) Длина дуги окружности и площадь кругового сектора.

Глоссарий по теме

Окружность – это замкнутая линия, все точки которой равноудалены от центра.

Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.

Круг – часть плоскости, ограниченная окружностью.

Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.

Круговой сектор – часть круга, ограниченная двумя радиусами.

Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Теоретический материал для самостоятельного изучения

На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.

Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.

На окружности можно выделить дугу. А если рассмотреть круг — часть плоскости, ограниченной окружностью — то можно выделить круговой сектор.

«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей

Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)

Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, . А учитывая, что R=1, , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.

Вычислите длину каждой дуги.

Ответ. длина каждой дуги равна части окружности или

Длина полуокружности равна А так как образовался развернутый угол, то 180.

Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.

рис.3

Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Обозначается 1рад.

;

α рад=(180/π α)° (1)

Длину дуги l окружности радиуса R (рис.4)

можно вычислять по формуле(3)

А площадь S кругового сектора радиуса R и дугой рад (рис.5)

находят по формуле: , где (4)

Вернёмся к единичной окружности в координатной плоскости.

Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.

Введём понятие поворота точки. (рис.2)

Пусть Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Пусть точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.

При повороте на 0 рад точка остаётся на месте.

Давайте рассмотрим такой пример:

при повороте точки М(1;0) на угол получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на

угол (рис.6)

(рис.6)

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Найти градусную меру угла, равного рад.

Решение: Используя формулу (1),

находим .

Так как , то рад, тогда (2)

Ответ: .

Пример 2. Найти радианную меру угла, равного 60.

Решение:

Вычисляем по формуле (2): рад

рад

При обозначении мер угла, наименование «рад» опускают.

Ответ: рад, рад.

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера .

Решение: Используя формулу (3),

получим:

Ответ: .

Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла .

Решение:

По формуле (4) вычисляем

Ответ: 45 м²

Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный .

Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как то

прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны Учитывая, что точка М находится в I координатной четверти, её координаты положительны.

На окружности можно найти координаты любой точки.

Ответ:

Источник

Перевод градусов в радианы и обратно: формулы, примеры

Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.

Связь между градусами и радианами

Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.

Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.

Связь градусов с радианами

Связь между радианами и градусами выражается формулой

Формулы перевода радианов в градусы и наоборот

Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.

Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.

1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .

Также можно выразить один градус в радианах.

1 ° = π 180 р а д

Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.

1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °

Значит, в одном радиане примерно 57 градусов

1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д

Один градус содержит 0,0175 радиана.

Формула перевода радианов в градусы

x р а д = х · 180 π °

Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.

Примеры перевода градусов в радианы и радианов в градусы

Пример 1. Перевод из радианов в градусы

Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.

Применим формулу перехода от радианов к градусам и получим:

3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °

Аналогично можно получить формулу перевода из градусов в радианы.

Формула перевода из градусов в радианы

y ° = y · π 180 р а д

Переведем 47 градусов в радианы.

Согласно формуле, умножим 47 на пи и разделим на 180.

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №29. Радианная мера угла

Перечень вопросов, рассматриваемых в теме:

1) Понятие тригонометрической окружности;

2) Поворот точки вокруг начала координат;

3) Длина дуги окружности и площадь кругового сектора.

Глоссарий по теме

Окружность – это замкнутая линия, все точки которой равноудалены от центра.

Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.

Круг – часть плоскости, ограниченная окружностью.

Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.

Круговой сектор – часть круга, ограниченная двумя радиусами.

Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Теоретический материал для самостоятельного изучения

Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.

«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей

Вычислите длину каждой дуги.

Ответ. длина каждой дуги равна части окружности или

Длина полуокружности равна А так как образовался развернутый угол, то 180.

рис.3

;

α рад=(180/π α)° (1)

Длину дуги l окружности радиуса R (рис.4)

можно вычислять по формуле(3)

А площадь S кругового сектора радиуса R и дугой рад (рис.5)

находят по формуле: , где (4)

Вернёмся к единичной окружности в координатной плоскости.

Введём понятие поворота точки. (рис.2)

Пусть Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Пусть точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.

При повороте на 0 рад точка остаётся на месте.

Давайте рассмотрим такой пример:

угол (рис.6)

Примеры и разбор решения заданий тренировочного модуля

Найти градусную меру угла, равного рад.

Решение: Используя формулу (1),

находим .

Так как , то рад, тогда (2)

Ответ: .

Пример 2. Найти радианную меру угла, равного 60.

Вычисляем по формуле (2): рад

рад

При обозначении мер угла, наименование «рад» опускают.

Ответ: рад, рад.

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера .

Решение: Используя формулу (3),

получим:

Ответ: .

Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла .

По формуле (4) вычисляем

Ответ: 45 м 2

Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный .

Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как то

На окружности можно найти координаты любой точки.

Ответ:

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Числовая и единичная окружность

В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.

Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.

Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:

Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.

Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.

Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:

В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.

Выглядит единичная окружность так:

Откладывание углов на единичной окружности

Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:

Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.

Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:

Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:

Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:

В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.

Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:

Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:

Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:

Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.

Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:

С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:

Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:

Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:

Например, верны следующие равенства:

15° + 3•360° = 15° + 1080° = 1095°

100° + 10•360° = 100° + 3600° = 3700°

1000° = 1000° – 2•360° = 1000° – 720° = 280°

Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5

источники:

http://resh.edu.ru/subject/lesson/4733/conspect/

http://100urokov.ru/predmety/urok-1-edinichnaya-okruzhnost

Источник

Лицензионное соглашение

Все материалы, размещённые на этом сайте, могут быть свободно использованы в некоммерческих целях при условии сохранения авторства. Без письменного согласия автора ЗАПРЕЩАЕТСЯ:

публикация материалов в любой форме, в том числе размещение материалов на других Web-сайтах;
распространение неполных или измененных материалов;
включение материалов в сборники на любых носителях информации;
получение коммерческой выгоды от продажи или другого использования материалов.

Скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.

Источник

Угол может измеряться следующими величинами:

Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
Радианами.

Градусная мера угла

Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.

Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.

Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.

Радианная мера угла

Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.

Длина окружности равна:

l=2⋅π⋅rl=2cdotpicdot r,

где rr — радиус этой окружности.

Тогда, разделив на радиус, получаем, что полный угол в радианах равен:

lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}

В градусах этот же угол равен, как известно, 360∘360^{circ}.

Отсюда находим связь между радианами и градусами:

2⋅π радиан=360∘2cdotpitext{ радиан}=360^{circ}

Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.

Один радиан равен:

1 радиан=360∘2⋅π≈57.3∘1text{ радиан}=frac{360^{circ}}{2cdotpi}approx57.3^{circ}

Один радиан в минутах:

1 радиан=360∘2⋅π⋅60≈3438′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60approx3438′

Один радиан в секундах:

1 радиан=360∘2⋅π⋅60⋅60≈206280′′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60cdot60approx206280»

Перевод градусов в радианы

Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.

Перевод градусов в радианы

y радиан=π180⋅xytext{ радиан}=frac{pi}{180}cdot x

xx — значение угла в градусах;
yy — значение того же угла в радианах.

Пример 1

Переведите 45 градусов в радианную меру измерения. Ответ округлите до десятой доли.

Решение

45∘=π180⋅45 радиан≈0.8 радиан45^{circ}=frac{pi}{180}cdot 45text{ радиан}approx0.8text{ радиан}

Ответ

0.8 радиан0.8text{ радиан}

Задача

Земля совершила треть от половины оборота вокруг Солнца. На какой угол в радианах она повернулась?

Решение

Найдем сначала этот угол в градусах. Полный угол составляет 360∘360^circ. Половина от полного оборота это 180∘180^{circ}. Нам же нужна треть этого угла, то есть:

180∘3=60∘frac{180^circ}{3}=60^circ

Земля отклонилась на угол 60∘60^circ от своего начального положения. Переведем теперь этот угол в радианы:

60∘=π180⋅60 радиан≈1 радиан60^circ=frac{pi}{180}cdot 60text{ радиан}approx1text{ радиан}

Решение

1 радиан1text{ радиан}

Перевод радиан в градусы

Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.

Перевод радиан в градусы

y∘=180π⋅xy^{circ}=frac{180}{pi}cdot x

xx — значение угла в радианах;
yy — значение того же угла в градусах.

Пример 2

Переведите 3 радиана в градусную меру угла.

Решение

3 радиана=180π⋅3≈172∘3text{ радиана}=frac{180}{pi}cdot3approx172^circ

Ответ

172∘172^circ

Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!

Тест по теме «Перевод градусов в радианы и наоборот»

Источник

Материалы урока

Прежде, чем приступить к рассмотрению новой темы, давайте вспомним, что градусом называют величину центрального угла, которому соответствует 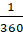часть окружности. Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в измеряемом угле.

А углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.

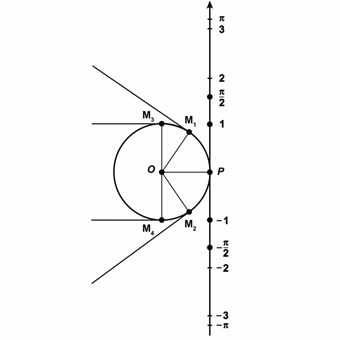
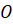
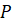
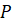
Давайте изобразим окружность с центром в точке и радиусом . Затем проведём вертикальную прямую, которая касается окружности в точке . Эту прямую мы будем считать числовой осью с началом отсчёта в точке . Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.

Отметим на прямой несколько точек: и , и , и , и , и .

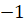
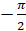
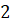
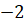
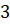
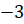
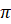
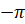
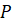
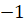
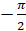
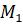
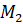
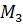
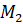
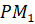
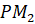
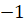
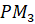
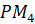
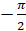
Теперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке . Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами , , , перейдут соответственно в точки окружности , , , . При этом длина дуги равна , длина дуги равна , длина дуги равна , длина дуги равна .

Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.

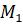
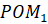
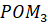
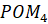
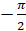
Так, точке прямой с координатой ставится в соответствие точка . А значит, угол можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол следует считать равным , а угол равным .

А где используют такой способ измерения углов? Такой способ измерения углов широко используется в математике и физике. Говорят, что углы измеряются в радианной мере.

Единичный угол 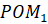называют углом в один радиан. Записывают так: рад.

И напомним, что длина дуги 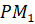равна радиусу нашей окружности.

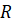
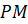
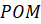
Сейчас давайте рассмотрим окружность радиуса . И отметим на ней дугу , равную длине радиуса окружности, и угол .

И такой угол называется углом в один радиан? Верно.

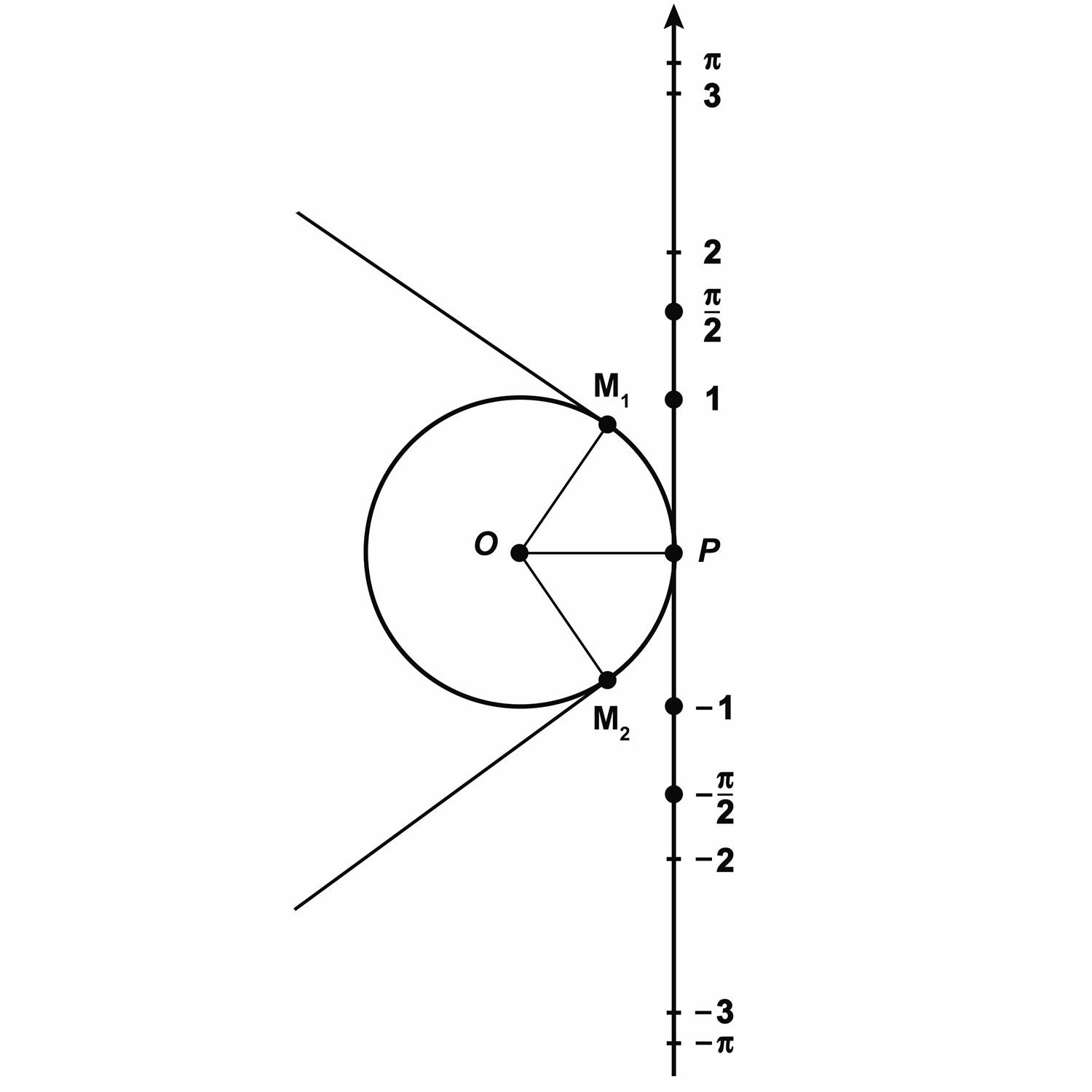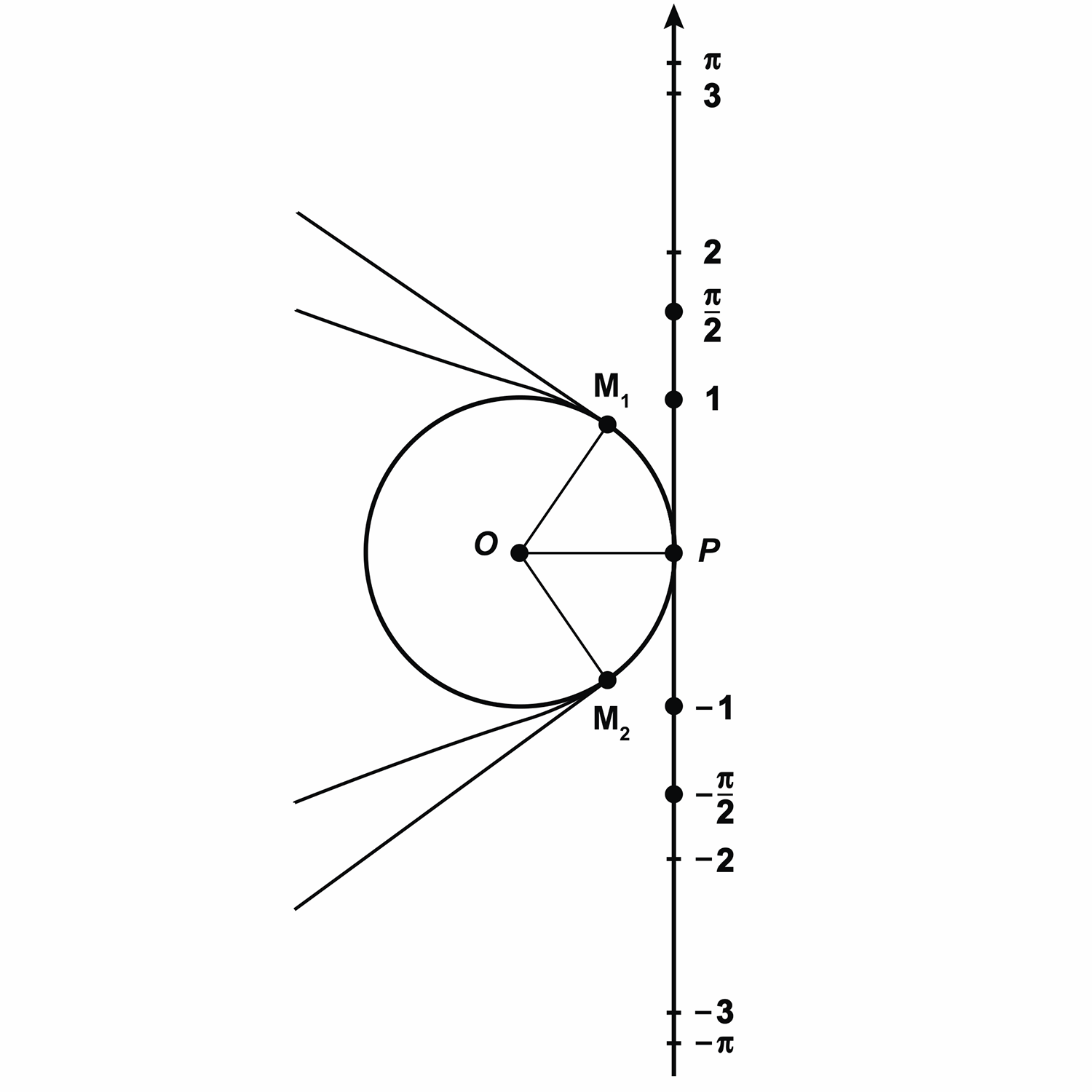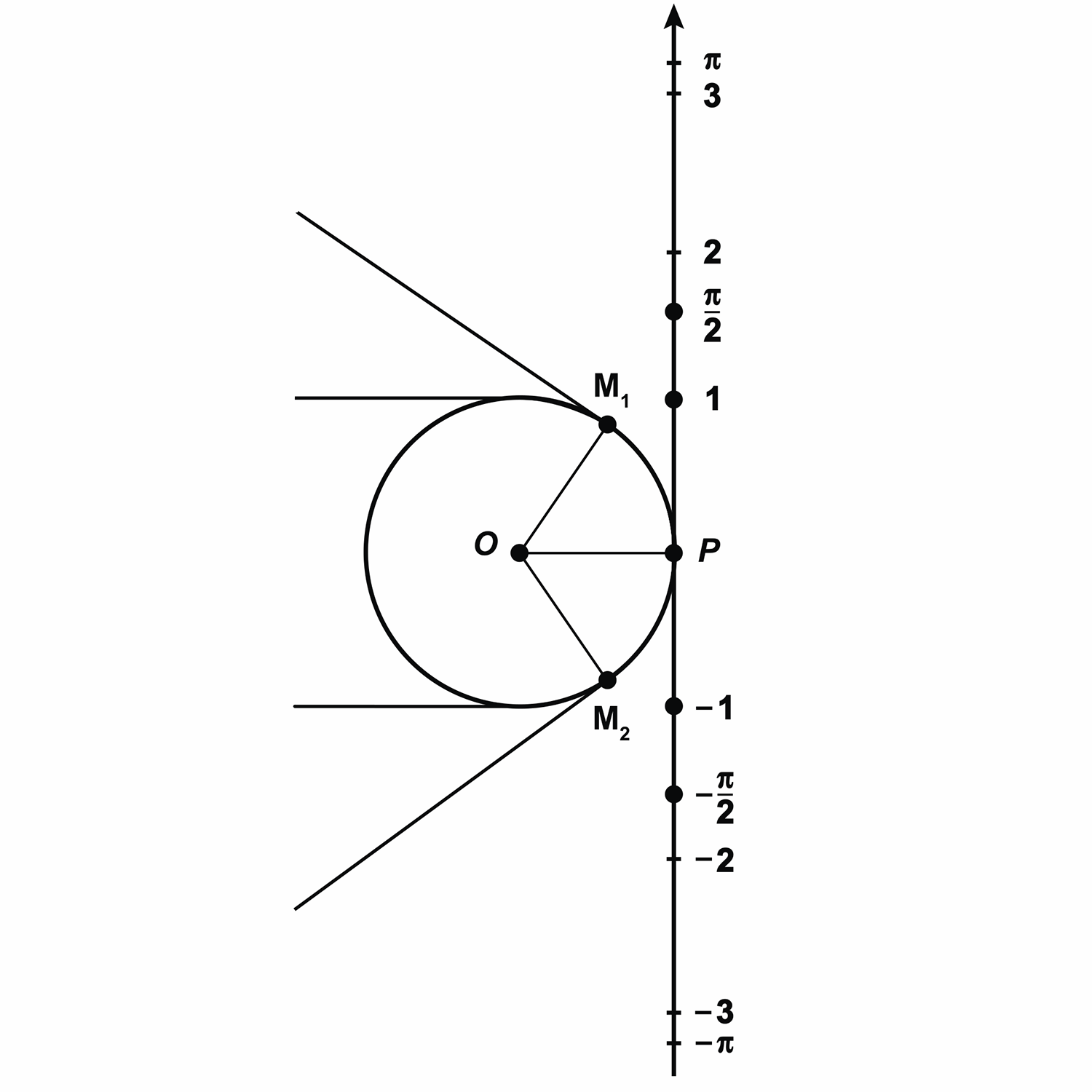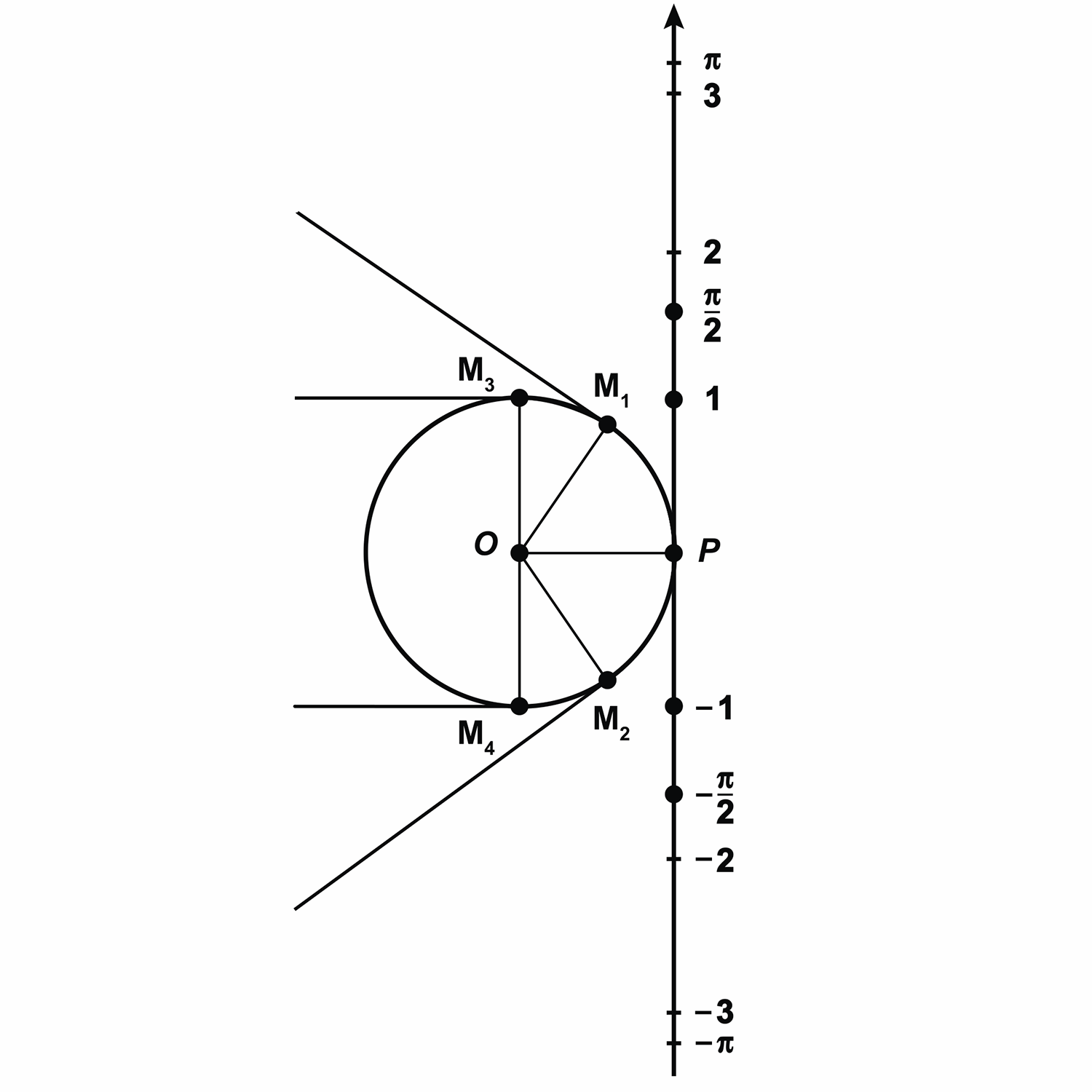
Запомните! Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.

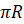
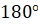
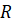
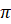
Интересно, а скольким градусам равен угол в один радиан? Давайте найдём градусную меру угла в один радиан. Мы знаем из курса геометрии, что дуге длиной , то есть полуокружности, соответствует центральный угол, равный . Следовательно, дуге окружности длиной соответствует угол в раз меньший.

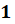
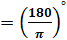
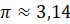
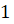
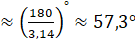
Выше мы назвали такой угол углом в один радиан, а значит, можем записать, что рад . , тогда рад .

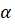
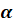
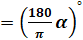
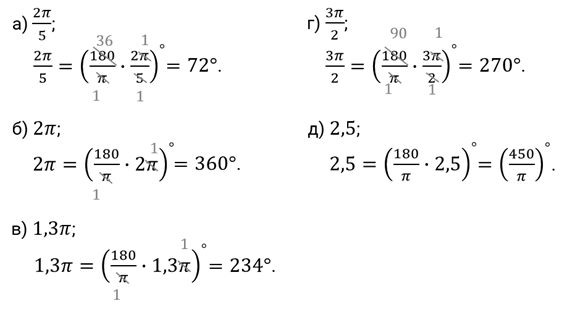
Если угол содержит рад, то рад . Эту формулу называют формулой перехода от радианной меры к градусной.

Давайте с вами найдём градусную меру угла, равного рад. Для этого воспользуемся формулой перехода от радианной меры к градусной. Подставим вместо : . Сократим на и на . И в результате получим .

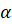
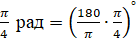
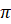
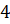
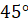
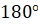
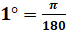
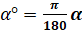
Можно ли, наоборот, перейти от градусной меры к радианной? Конечно, можно, но такой переход будет чуть сложнее. Так как угол в равен рад, то рад. Тогда рад. Такую формулу называют формулой перехода от градусной меры к радианной.

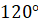
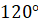
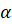
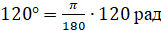
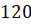
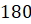
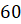
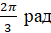
Найдём радианную меру угла, равного . Воспользуемся формулой перехода от градусной меры к радианной. Подставим вместо : . Сократим и на . И в результате получим .

Обратите внимание, что при обозначении меры угла в радианах слово «радиан» обычно не пишут: 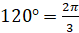. При этом обозначение градуса в записи меры угла пропускать нельзя.

В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.

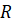
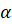
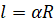
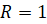
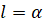
Отметим, что радианная мера углов позволяет значительно упростить многие формулы в математике, физике, механике. В частности, радианная мера угла удобна для вычисления длины дуги окружности. Так, выше мы выяснили, что угол в рад стягивает дугу, длина которой равна радиусу , а значит, угол в рад стягивает дугу длиной: . Если , то эта формула принимает совсем простой вид: , то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.

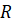
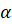
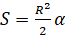
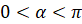
Сейчас, прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового сектора радиуса , образованного углом в рад, равна , где .

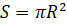
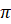
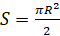
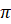
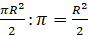
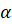
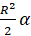
Докажем это. Известно, что площадь круга вычисляется по формуле: . Площадь полукруга, то есть кругового сектора в рад: . Тогда площадь сектора в рад в раз меньше, то есть . Следовательно, площадь сектора в рад равна .

Ну а сейчас давайте выполним несколько заданий.

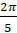
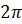
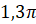
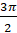
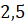
Первое задание. Найдите градусную меру угла, выраженную в радианах: а) ; б) ; в) ; г) ; д) .

Решение.

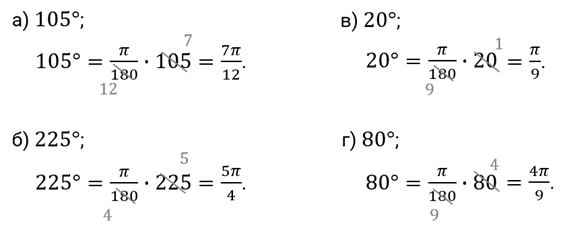
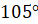
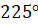
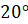
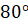
Второе задание. Найдите радианную меру угла, выраженного в градусах: а) ; б) ; в) ; г) .

Решение.

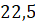
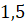
Следующее задание. Чему равен радиус окружности, если дуге длиной см соответствует центральный угол в рад?

Решение.

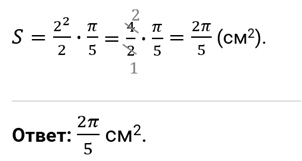
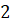
И ещё одно задание. Дуге кругового сектора соответствует угол, равный рад. Чему равна площадь сектора, если радиус круга равен см?

Решение.

Ну а сейчас немного истории.

Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.

В 1960 году XI Генеральной конференцией по мерам и весам радиан был принят в качестве единицы измерения плоских углов в Международной системе единиц (СИ).

Источник