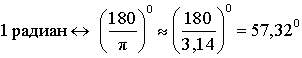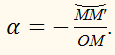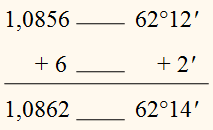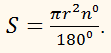Как найти радианную меру углов треугольника

Задание Найдите радианную
меру большего острого угла прямоугольного треугольника, величины острых углов
которого относятся как 1:6.

Варианты ответов.

Теория Формула перевода
градусной меры угла в радианную: α°=α°∙π/180°. Сумма острых углов
прямоугольного треугольника равна 90°.

Анализ В условии замечаем
соотношение, в котором связаны величины острых углов, это значит, вводим
коэффициент пропорциональности k, тогда один угол будет 1k,
а второй – 6k. Связываем углы уравнением 1k+6k=90°

Решение

7k=90

k=90/7

Тогда больший угол равен 6k=6∙(90/7)°=(6∙90°)/7. Переводим в
радианы:

Ответ. 3

Измерение углов. Градусы и радианы

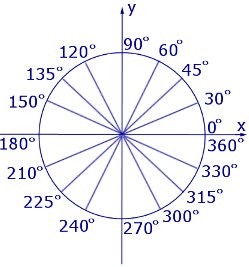
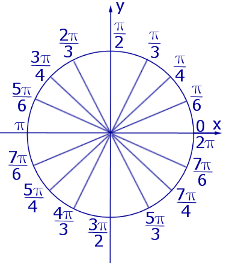
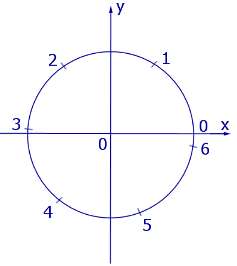
Рассмотрим тригонометрические круги, изображенные на рисунке 1 и рисунке 2.

Рис.1

Рис.2

На тригонометрическом круге, изображенном на рисунке 1, центральные углы измерены в градусах, а на тригонометрическом круге, изображенном на рисунке 2, те же центральные углы измерены в радианах.

Углом в   1   градус называют угол, составляющий     полного угла. Углом в   k°   называют угол в   k   раз больший угла в   1° .

Углом в   1   радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной   1 .   Углом в   k   радиан называют центральный угол тригонометрического круга в   k   раз больший угла в   1   радиан.

СЛЕДСТВИЕ 1. Углом в   k   радиан является центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной   k .

СЛЕДСТВИЕ 2. Полный угол является углом в   2π   радиан.

Для того, чтобы найти формулы, связывающие градусную и радианную меры угла, рассмотрим рисунки 3 и 4

На этих рисунках изображены прямые углы, причем на рисунке 3 прямой угол измерен в градусах и равен   90° ,   а на рисунке 4 прямой угол измерен в радианах и равен  радиан. Следовательно,

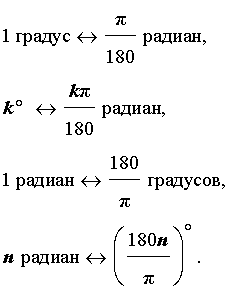
Таким образом, формулы, связывающие градусную и радианную меры угла, имеют вид

Поскольку , то

По этой причине углы, составляющие целое число радиан, изображаются на тригонометрическом круге так, как это показано на рисунке 5.

Рис.5

ЗАМЕЧАНИЕ. Тригонометрическая формула sin α означает, что рассматривается синус угла в   α   радиан, а тригонометрическая формула   sin α°   означает, что рассматривается синус угла в   α   градусов. По такому же правилу определяются значения косинуса, тангенса и котангенса.

ПРИМЕР. Найти наименьшее из чисел:

РЕШЕНИЕ. Поскольку

то наименьшим числом является число     cos 3 .

ВИДЕО УРОК

Помимо градусной меры
углов существует так называемая радианная мера. Эта мера широко используется в
тригонометрии, в математическом анализе и в его приложениях.

Рассмотрим
произвольный положительный угол  α. Возьмём на
стороне  ОА  этого угла

 произвольную точку  М,
не совпадающую с вершиной  О  угла. Пусть 

– путь, который
пройдёт точка  М, если произвести указанный поворот  α  от  ОА  к  ОВ.

Радианной мерой
угла  α  называется отношение этого пути к
радиусу  ОМ.
Радианную меру угла условимся обозначать той же буквой, что и сам угол:

Если  α –
отрицательный угол,

то радианной мерой
назовём отрицательное число:

Радианная мера угла определяется только
углом.

Единицей при радианном
измерении углов служит радиан.

Радианом называется
центральный угол, опирающийся на дугу окружности, длина которой равна длине
радиуса той же окружности.

В основе определения радиана – всё равно окружность.
Угол в  1  радиан, это
угол, который вырезает из окружности дугу, длина которой (L) равна длине радиуса
(R).

Соотношение между радианом и градусом.

На рисунке этот малюсенький
угол имеет величину  1 градус:

Один радиан много больше одного градуса. А во сколько раз ?

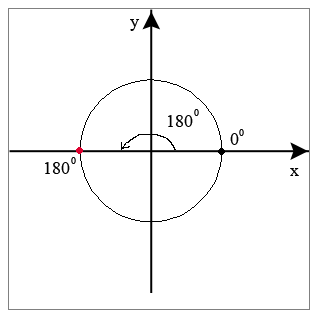
 Смотрим следующую картинку. Развёрнутый угол размером в  180°.

А теперь нарежем этот полукруг радианами.

 Видим, что в  180°  укладывается  3  с хвостиком
радиана. Этот хвостик – 0,1415926 … .

Действительно, в 
180°  укладывается  3,1415926… радиан. Всё время
писать 3,1415926… неудобно. Поэтому
вместо этого бесконечного числа всегда пишут просто:

π

Вот теперь можно записать приближённое равенство:

180° ≈ 3,14 радиан

Или точное равенство:

180° = π радиан

Определим, сколько градусов в
одном радиане. Если в  3,14  радианах  180°  градусов, то в  1  радиане в  3,14  раз меньше! То есть, мы делим
первое уравнение (формула – это тоже уравнение!) на 3,14:

В одном радиане примерно  60°.

Человек видит «Пи» и считает, что это  180°. Но «Пи» – это число! Число  3,14, а никакие не градусы! Это «Пи» радиан = 180°!

Ещё раз: «Пи» – это число! 3,14. Иррациональное, но
число. Такое же, как  5  или  8. Можно, к примеру,
сделать примерно «Пи» шагов. Три шага и ещё немножко. Или купить
«Пи» килограммов конфет. Если продавец образованный попадётся…

Перевод градусов в радианы и
обратно.

Если угол задан в радианах с числом «Пи»,
всё очень просто. Мы знаем, что

«Пи» радиан
= 180°.

Вот и подставляем вместо «Пи» радиан – 180°. Получаем угол в
градусах. Сокращаем, что сокращается, и ответ готов.

ПРИМЕР:

Нужно выяснить, сколько градусов в угле «Пи»/2 радиан.

Или:

Обратный перевод чуть сложнее. Если угол дан в градусах,
мы должны знать, чему равен один градус в радианах, и умножить это число на
количество градусов.

ПРИМЕР:

Чему
равен  1°  в радианах ?

Смотрим на формулу и видим, что если  180° = «Пи» радиан,
то  1°  в  180  раз меньше. Или, другими словами, делим
уравнение (формула – это тоже уравнение!) на  180:

Умножаем
число градусов на это значение и получаем угол в радианах.

ПРИМЕР:

 Или, аналогично:

Чтобы найти радианную
меру любого угла по его данной градусной мере, надо умножить число градусов на

число минут – на

число секунд – на

и сложить найденные произведения.

ПРИМЕР:

Выразить в радианах угол,
равный  22°30‘.

РЕШЕНИЕ:

Искомое число радианов получим, умножив

ПРИМЕР:

Найти радианную меру угла  12°30‘  с точностью до четвёртого
десятичного знака.

РЕШЕНИЕ:

Умножим  12  на  0,017453 

получим  ≈ 0,2094.

Умножим  30  на  0,000291 

получим  ≈ 0,00873.

12°30‘ ≈ 0,2094 + 0,00873 ≈ 0,2181
рад.

Чтобы
найти градусную меру любого угла по его данной радианной  мере, надо умножить число радиан на

(относительная
погрешность результата составит 0,0004%,
что составляет абсолютной погрешности  5»  для полного оборота  360°).

ПРИМЕР:

Выразить в градусах угол,
равный  ^𝜋/₁₂ радианов.

РЕШЕНИЕ:

Имеем:

ПРИМЕР:

Найти градусную меру угла  1,4
рад  с точностью
до  1‘.

РЕШЕНИЕ:

Последовательно найдём

1 рад ≈ 57°17‘45»,

0,4
рад ≈ 0,4×57°.296
= 22°.9184,

0°.9184×60 ≈ 55‘.104,

0‘.104×60 ≈ 6».

Таким
образом

0,4
рад ≈
22°55‘6».

И тогда:

1 рад ≈ 57°17‘45»  +  0,4 рад ≈
22°55‘6»

 = 1,4 рад ≈ 80°12‘51».

После
округления этого результата до требуемой точности в  1‘  окончательно
получим

1,4
рад ≈
80°13‘.

В обозначении меры угла в радианах почти всегда опускают
слово <<радиан>>. Таким образом, записи

α =
2, α = ¹/₂, α = ⁷/₉

надо понимать как

α =
2 радиана,

α =
¹/₂ радиана,

α = ⁷/₉ радиана.

ПРИМЕР:

Выразить в градусах угол  α, равный  2.

РЕШЕНИЕ:

Имеем:

α ≈ 57°3 ∙ 2 ≈ 114°6.

Широко распространено соглашение, по которому под словом <<угол>>
подразумевают не угол как геометрический образ, а число, измеряющее его в
радианах или градусах.

ПРИМЕР:

Угол  ^π/₂, угол  36°,
угол  1.

 В частности, в
выражениях типа  <<угол
поворота>> под словом <<угол>>  понимается обычно мера угла.

Таблица соотношений между градусным и радианным
выражениями некоторых углов.

Для облегчения вычислительной работы при переходе от
градусной меры угла к радианной и обратно пользуются специальными таблицами.

Отметим, что радианная мера одного полного
оборота

 равна:

Если углы измерены в градусах, то один полный
положительный оборот будет равен  360°. Отсюда вытекают следующие соотношения:

360° = 2π (≈
6,2832) радианов,

270° = ^3𝜋/₂ (≈ 4,7124) радианов,

180° = π (≈ 3,1416)
радианов,

 90° = ^𝜋/₂ (≈ 1,5708) радианов,

 60° = ^𝜋/₃ (≈ 1,0472) радианов,

 45° = ^𝜋/₄ (≈ 0,7854) радианов,

 30° = ^𝜋/₆ (≈ 0,5236) радианов.

Как пользоваться таблицами Брадиса ?

В книге В. Брадиса <<Четырёхзначные математические таблицы>>
под номером  XVI  помещена таблица, которая озаглавлена
<<Радианная мера>>.

Пометка в скобках
расшифровывается так: дуга, содержащая  A°, равна

радианов.

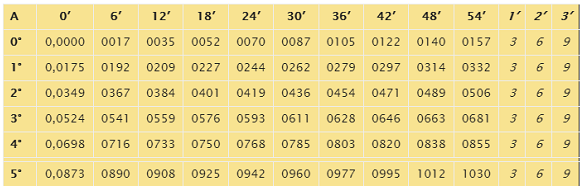
В левом столбце таблицы
под буквой  А  даны
числа градусов, содержащихся в угле, а в верхней и самой нижней строках – числа
минут, кратных  6.

Покажем на примерах как пользоваться этой таблицей.

ПРИМЕР:

Угол  71°24‘  перевести в радианы.

РЕШЕНИЕ:

На пересечении строки,
начинающейся с  71°, и столбца, помещённого
вверху  24‘,
читаем:

1,2462

(число целых указывается в таблице в начале строки и дальше даются
только десятичные знаки).

При переводе в радианы угла с любым числом минут, не кратным  6, пользуются соответствующими поправками, которые помещены
в последних трёх столбцах под числами минут:

1‘, 2‘,
3‘.

ПРИМЕР:

Угол  23°20‘  перевести в радианы.

РЕШЕНИЕ:

Имеем:

Данный угол  23°20‘  равен  0,4073  радиана.

 ПРИМЕР:

Найти градусное выражение угла,
содержащего  1,0862 радиана.

РЕШЕНИЕ:

Имеем из таблицы:

Данный угол равен  62°14‘.

Когда то в Древнем Египте мучились следующим вопросом. Во
сколько раз длина окружности больше длины её диаметра? И так измеряли, и
этак… Всё получалось немного больше трёх. Пока окончательно не доказали, что
как бы мелко не нарезать окружность на равные кусочки, из таких кусочков
составить ровно длину диаметра нельзя… В принципе нельзя.
Ну, во сколько раз окружность больше диаметра установили. Примерно. В  3,1415926… раз.

Это и есть число
«Пи». После запятой – бесконечное число цифр без всякого порядка…
Такие числа называются иррациональными. Это и означает, что из равных кусочков
окружности диаметр ровно не сложить. Никогда.

Для практического применения принято запоминать всего
две цифры после запятой:

π = 3,14.

Так как длина окружности больше диаметра в
«Пи» раз, имеет смысл запомнить формулу длины окружности:

L = π d

где  L – длина окружности,
а  d – её диаметр. 

При радианном измерении углов заметно упрощается ряд формул. Так, для окружности
радиуса  r  длина  l  его дуги  α  радиан можно
найти по формуле

l
= αr,

площадь S  сектора круга радиусом  r, в дуге которого находится  α  радиан, вычислим по формуле

Эти формулы проще, чем аналогичные формулы

и

Для вычисления дуги окружности и площади
сектора, дуги которых (величиной  n°) измеряются с помощью
градусной меры. Эти особенности радианной меры привели к тому, что в
тригонометрии отдают преимущество радианному, а не градусному измерении.

Радианная и градусная мера угла

5 мая 2014

Сегодняшний видеоурок — один из ключевых в курсе тригонометрии. Мы расширим классическое определение синуса, косинуса и тангенса на произвольные углы (в т.ч. отрицательные), а введем новое определение — радианную меру угла.

Сегодня мы поговорим о такой теме, которая волнует всех учеников 8-9 классов, когда они начинают изучать серьезную взрослую тригонометрию. Речь идет о радианной мере угла, а также о переводе из радианной в градусную меру угла и обратно. Но, прежде чем мы начнем решать какие-то задачи на вычисления радианной меры, мне хотелось бы вспомнить старое определение, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Немного теории

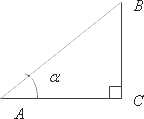
Давайте нарисуем прямоугольный треугольник, назовем его

, причем CC будет прямым:

Угол AA будет равен αalpha градусов. В этом случае, как вы помните из школьного курса геометрии, синус, косинус и тангенс будут одинаковые:

sinα=BCAB

sin alpha =frac{BC}{AB}

cosα=ACAB

cos alpha =frac{AC}{AB}

tgα=BCAC

tgalpha =frac{BC}{AC}

Как видите, классическое определение синуса, косинуса, тангенса и котангенса завязано на прямоугольном треугольнике, и αalpha в любом случае должен быть больше 0º и меньше 90º.

Несмотря на это, возникла необходимость расширить определение тригонометрических функций за пределы этого интервала от 0º до 90º. Как это происходит, и какие возникают при этом эффекты — вот сейчас об этом и поговорим.

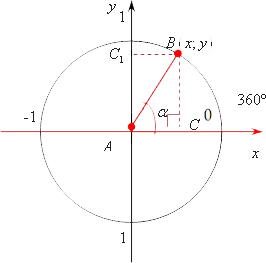
Для начала давайте рассмотрим координатную плоскость: проведем оси xx, yy, а также построим единичную окружность с центром в начале координат:

 

Небольшое уточнение в терминологии, что значит единичная окружность? Все очень просто. Это означает, что ее радиус равен строго 1. Другими словами, она проходит через точку (1; 0), а также (0; 1). И через две остальные точки эта окружность также проходит. Теперь нам нужно пустить от начала координат луч вдоль оси OxOx. Речь идет о положительном направлении оси OxOx. Затем мы отметим αalpha в направлении xx к yy. Разумеется, этот луч пересечет наш круг в неком значении, давайте обозначим его точкой BB. А начало координат обозначим точкой AA. Проведем из BB высоту к оси абсцисс xx. Мы получим CC. Вот мы снова получили тот же самый прямоугольный треугольник ABCABC с углом αalpha , вершина которого совпадает с началом координат.

Что такое синус?

Теперь давайте перепишем синус, косинус и тангенс с учетом всех изменений для красного треугольника. Запишем:

sinα=BCAB

sin alpha =frac{BC}{AB}

Все то же самое. Однако заметим, что BB лежит уже не в каком-то неопределенном пространстве, она имеет какие-то координаты, поскольку лежит в плоскости OxyOxy. Пусть ее координаты будут (x;y)left( x;y right). Мы не знаем точно, чему они равны, потому что не знаем угол αalpha . В таком случае длина отрезка BCBCравняется yy, т. е. ординате точки BB. Вместо BCBC мы можем записать yy, а вместо ABAB — 1. ABAB — это тот же самый радиус нашего круга, а радиус — 1. Записываем:

sinα=BCAB=yr=y

sin alpha =frac{BC}{AB}=frac{y}{r}=y

Таким образом, мы можем записать, что sinαsin alpha на самом деле равен ординате конца подвижного радиуса. Вот именно эту фразу чаще всего встречают ученики в школьных учебниках по математике. Поэтому, прежде чем двинемся дальше, давайте еще раз внимательно посмотрим на треугольник ABCABC и, в частности, на BB.

Мы провели еще одну высоту, назовем ее BC1B{{C}_{1}}. Что можно сказать про C1{{C}_{1}}, точнее, про отрезок AC1A{{C}_{1}} — это координата у BB. С другой стороны, отрезок ACAC, т. е. расстояние от AA до CC — это координата xx точки CC и, соответственно, xx точки BB. Нам несложно будет доказать, что отрезки BCBC и AC1A{{C}_{1}} равны. Тогда мы можем утверждать, что и отрезок ABAB тоже равен yy. Таким образом, с синусом мы разобрались. Действительно, синус угла αalpha равен ординате конца подвижного радиуса, проведенного в точку BB. Теперь давайте запишем те же самые выражения для косинуса и тангенса.

Что такое косинус? 

Это отношение прилежащего катета (в нашем случае это катет ACAC) к гипотенузе (у нас ABAB). Но что такое ACAC? Только что мы убедились, что ACAC — это абсцисса, т. е. координата xx. А ABAB — это тот же самый радиус, т. е. 1. Запишем:

cosα=ACAB=xr=x

cos alpha =frac{AC}{AB}=frac{x}{r}=x

Что такое тангенс?

Теперь разбираемся с tgαtgalpha . Тут все еще проще. Что такое тангенс? Это отношение противолежащего катета (а нашем случае это BCBC) к прилежащему катету (в нашем случае это ACAC). Запишем:

tgα=BCAC=yx

tgalpha =frac{BC}{AC}=frac{y}{x}

Таким образом, tgtg — это отношение ординаты к абсциссе конца подвижного радиуса.

И в этот момент многие ученики наверняка спросят: «А зачем вообще вся эта сложность?». В данном случае когда BB просто задается пересечением луча с окружностью, мы можем отложить любой угол αalpha . Теперь никаких ограничений на обозначение αalpha не накладывается. Он не обязан быть углом пределах от 0º до 90º.

Вычисление радианной меры угла

Теперь, когда мы разобрались с основными определениями тригонометрических функций, перейдем непосредственно к сегодняшней теме урока.

Для начала давайте рассмотрим угол в 180º. Тогда наш луч поддет в противоположном направлении. Точка В в нашем треугольнике высекает определенную дугу окружности. Назовем ее дуга BCBC. Ее легко посчитать по формуле длины окружности:

l=2πr

l=2pi r

π ˜3,14

pi tilde{ }3,14. Но сейчас нас это не интересует. Поскольку наша окружность всегда имеет фиксированный радиус 1, то длина будет равна:

l=2π

l=2pi

Однако 2π2pi — это вся окружность, т. е. полный оборот. А мы если отступим на 180º, то получим только ее половину. Следовательно, дуга окружности будет равна:

l(180o)=2π2=π

lleft( 180{}^text{o} right)=frac{2pi }{2}=pi

И вот тут возникает замечательный эффект. Дело в том, что один и тот же угол αalpha мы можем обозначать как за 180º, т. е. использовать стандартную меру угла (а не радианную), так и длинной вот этой дуги, т. е. мы можем поставить углу αalpha соответствующее число πpi . Так вот это число πpi , т. е. другими словами, угол, измеренный не в градусах, а в длине дуги, которую этот угол высекает. Называется это радианная мера угла и обозначается πpi — радиан.

Сегодня же для того чтобы начать решать задачи на радианную меру и считать значение тригонометрических функций, просто запомните, что πpi рад = 180º. Другими словами, если вам непривычно работать с радианными значениями, то везде, где вы видите в синусах, косинусах и тангенсах конструкцию πpi , вы можете смело заменить это π на 180º и перейти к знакомой градусной от радианной меры. Давайте попробуем и сосчитаем первое выражение и найдем радианную меру:

sin π 4cos π 6tg π 3=2√2⋅3√2⋅3√=32√4sin frac{text{ }!!pi!!text{ }}{4}cos frac{text{ }!!pi!!text{ }}{6}tgfrac{text{ }!!pi!!text{ }}{3}=frac{sqrt{2}}{2}cdot frac{sqrt{3}}{2}cdot sqrt{3}=frac{3sqrt{2}}{4}

Давайте выпишем отдельно каждую из этих функций:

sin π 4=sin180∘4=sin45∘=2√2sin frac{text{ }!!pi!!text{ }}{4}=sin frac{180{}^circ }{4}=sin 45{}^circ =frac{sqrt{2}}{2}

cos π 6=cos180∘6=cos30∘=3√2cos frac{text{ }!!pi!!text{ }}{6}=cos frac{180{}^circ }{6}=cos 30{}^circ =frac{sqrt{3}}{2}

tg π 3=tg180∘3=tg60∘=3√tgfrac{text{ }!!pi!!text{ }}{3}=tgfrac{180{}^circ }{3}=tg60{}^circ =sqrt{3}

Теперь записываем все три множителя в единую конструкцию для нахождения радианного значения. Вот и все, мы получили ответ.

Переходим ко второму выражению и найдем радианную меру:

cos π 3sin π 4ctg π 6=12⋅2√2⋅3√=6√4cos frac{text{ }!!pi!!text{ }}{3}sin frac{text{ }!!pi!!text{ }}{4}ctgfrac{text{ }!!pi!!text{ }}{6}=frac{1}{2}cdot frac{sqrt{2}}{2}cdot sqrt{3}=frac{sqrt{6}}{4}

Опять записываем каждую функцию отдельно:

cos π 3=cos60∘=12cos frac{text{ }!!pi!!text{ }}{3}=cos 60{}^circ =frac{1}{2}

sin π 4=sin45∘=2√2sin frac{text{ }!!pi!!text{ }}{4}=sin 45{}^circ =frac{sqrt{2}}{2}

ctgπ6=ctg30∘=3√ctgfrac{pi }{6}=ctg30{}^circ =sqrt{3}

Опять собираем все полученные числа.

Как видите, ничего сложно в радианных мерах угла нет. Если эта тема покажется вам слишком сложной, просто запомните, что πpi рад = 180º, и везде, где вы видите πpi , можете смело писать 180º.

Еще одним важным следствием нового определения тригонометрического круга является то, что синус, косинус и тангенс могут быть отрицательными. Если раньше все сводилось к длинам катетов и гипотенузы, то теперь перед нами абсциссы и ординаты некой точки. При этом помните, что откладывание угла всегда идет в направлении от оси OxOx к оси OyOy, причем идет речь именно о положительных направлениях этих осей.

Чтобы понять и навсегда запомнить, где находится положительное направление оси, просто помните правило: туда, куда указывает стрелка при х и при у, это и есть то самое положительное направление оси.

Вот это и все, о чем я хотел рассказать в сегодняшнем видеоуроке о радианных мерах. Если вы что-то не поняли, или если этот материал показался вам слишком сложным, то пересмотрите его еще раз, попробуйте выполнить всю последовательность вычислений на нахождения радианных значений, которую мы сегодня выполнили на уроке.  

Смотрите также:

1. Как быстро запомнить таблицу синусов и косинусов
2. Синус, косинус, тангенс, котангенс — геометрическая тригонометрия
3. Метод узлов в задаче B5
4. Тест к уроку «Сложение и вычитание дробей» (средний)
5. Иррациональное уравнение: учимся решать методом уединения корня
6. Задача B4: строительные бригады

Радиан — основная единица измерения плоских углов в математике.

Один радиан равен центральному углу окружности, длина дуги которого равна радиусу этой окружности:

radius (лат.) — луч, радиус

Радиан — это безразмерная величина, поскольку отражает соотношение длины дуги окружности к длине радиуса.

$$
angle POM = 1 text{ рад} = left ( frac{180}{pi}right)^{circ} approx 57,3 ^{circ}
$$

Величина полного угла равна 2π (два Пи) радиан, так как длина окружности — это 2π радиусов.

Неверно говорить, что π = 180°, правильно говорить π радиан = 180°, при этом π = 3,14…

При рассмотрении тригонометрических функций в математическом анализе всегда считается, что аргумент выражен в радианах, что упрощает запись. Само обозначение рад (rad) зачастую опускается. Радианы в силу своей математической «натуральности» позволяют более элегантно сформулировать ряд важных математических результатов.

Мое: мы живем на шаре. Земля у нас только одна, поэтому удобно принять ее радиус за 1. Мы ходим по поверхности, можем измерять пройденное расстояние по дуге. Поэтому очень естественно рассматривать углы на окружности. Никогда не понимала этого скачка от углов в прямоугольном треугольнике к углам в окружности — объяснение, что надо выйти за рамки острых углов ничего не объясняет.

Если я прошел по дуге 1 радиус земли, то на какой угол отклонился от первоначального положения? на 1 радиан — вводим единицу для измерения углов.

Какой смысл писать «я прошел 1 радиус Земли» или 1 метр или километр? мы все длины меряем в радиусах Земли, всегда имеем в виду радиус земли, других единиц нет — нет других планет и нет других народов, которые бы выбрали другую единицу длины. Если я один, буду ли я писать единицы измерения? нет, само собой, всегда подразумевается та единственная единица, которую я себе выбрал. В математике никогда не пишут единицы измерения длины, и не потому что длина — безразмерная величина, а потому что мы опускаем единицу измерения, абстрагируемся от нее. Но как только в задаче появляются см и дюймы, мы должны писать единицу измерения, чтобы не было неоднозначности. Или же сразу перевести все данные в задаче в одну систему.

Такие же рассуждения касаются угла. Радиан — это естественная единица измерения углов, другой в математике нет, и поэтому ее не пишут, опускают.

Радиан — это безразмерная величина, поскольку отражает соотношение длины дуги окружности к длине радиуса.

Нет, угол 1 радиан — это угол, соответствующий дуге, длина которой равна её радиусу. Если в задаче появляются градусы, румбы, грады или другие единицы измерения углов, то слово радиан опускать нельзя. Радиан — это и есть единица измерения, это не величина, и тем более не безразмерная величина.

Фактически, люди договорились, что если нет никакого слова при числе, выражающем меру угла — то угол измерен в радианах.

Википедия: Радианная мера — угловая мера, в которой за единицу принимается угол в 1 радиан. То есть, радианная мера любого угла — это отношение этого угла к радиану [сколько единичных углов помещается в наш измеряемый угол]. Из определения следует, что величина полного угла равна 2π радиан [R=1, 2π*1/1 = 2π]

Международное обозначение: rad. Если есть обозначение, то величина размерная.

Более того, есть 10³ рад = килорадиан = крад = krad, 10⁶ рад = мегарадиан = Мрад = Mrad и т.д.

Википедия: 1 радиан = 1/(2π) оборотов = 180/π градусов = 200/π градов.

Если один отрезок в 2 раза длиннее единичного отрезка, то мы же не говорим, что его длина является безразмерной величиной: 2 м / 1 м = 2 (метры сократились). Второй отрезок имеет длину 2 м, но в математике мы не пишем единицу измерения. Точно также — если расстояние по дуге в 2 раза больше радиуса окружности, это не значит что мера угла = 2, она равна 2 радианам, слово радиан опускаем для краткости.

Иначе нужно всегда когда речь идет об отношении двух длин говорить, что оно, отношение, измеряется в радианах.

И тут же фраза:

Неверно говорить, что π = 180°, правильно говорить π радиан = 180°

То есть сами признают, что слово радиан в этом контексте опускать нельзя — так как появились градусы, ситуация неоднозначная.

Википедия: Определить радианную меру можно и так: радианная мера угла — отношение длины дуги окружности, находящейся между сторонами угла, к радиусу этой окружности, когда центр окружности совпадает с вершиной угла. Так как величина угла, выраженная в радианах, равна отношению длины дуги окружности (м) к длине её радиуса (м), угол в радианном измерении — величина безразмерная.

Перепутали алгоритм расчета с сутью дела.

Википедия: Безразмерность плоского угла означает, что единицей его измерения является число один. Однако, применительно к плоскому углу единице «один» было присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно величина имеется в виду[9].

Как бы не выбирали единицу длины, угловая мера в радианах будет одинакова. Никак угловая мера угла не зависит от выбранной единицы длины. Если есть угол, у него есть угловая мера, и она не меняется если см заменить на м. Для измерения углов надо выбирать независимую единицу измерения — градус или радиан или град или оборот. Перл «единицей измерения угла является число один» вообще ни в какие ворота не лезет. Число — это уже единица измерения, оказывается.

Координаты точки — размерные или нет? Никогда не пишем (2 м; 3 м), но ведь всегда произносим — отсчитай 3 клетки вверх или 2 клетки вправо. Координаты измеряем в единичных отрезках. Длина отрезка — размерная величина. Число 1 в алгебре, оно ничего не знает о введенной метрике.

Далее, косинус и синус — размерные ли величины? если синус и косинус — отношение катета к гипонузе, то безразмерные. А если синус и косинус — координаты точки на единичной окружности, то может и размерные, так как чтобы найти координаты, нужно измерить расстояние до начала координат.

А если аксиоматически вводится скалярное произведение, а уже через него — длины и углы

Будем говорить, что в вещественном или комплексном векторном пространстве $L$ определено скалярное произведение, если каждой паре векторов $mathbf {a} ,mathbf {b} $ из $L$ поставлено в соответствие число $ (mathbf {a} ,mathbf {b} )$ из того числового поля, над которым задано $L$, удовлетворяющее следующим аксиомам.
1. линейность скалярного произведения по первому аргументу
2. Для любых $ mathbf {a} ,mathbf {b} $ справедливо равенство $(mathbf {a} ,mathbf {b} )={overline {(mathbf {b} ,mathbf {a} )}}$, где черта означает комплексное сопряжение.
3. Для любого $ mathbf {a} $ имеем: $ (mathbf {a} ,mathbf {a} )geqslant 0$, причём $ (mathbf {a} ,mathbf {a} )=0$ только при $ mathbf {a} =0$

Вводятся производные понятия:

• Длина вектора, под которой обычно понимается его евклидова норма: $ |mathbf {a} |={sqrt {(mathbf {a} ,mathbf {a} )}}$

• Углом $ varphi $ между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм): $ cos varphi ={frac {(mathbf {a} ,mathbf {b} )}{|mathbf {a} ||mathbf {b} |}} (0leqslant varphi leqslant pi ).$

Углом называется число, это раз. Косинус — безразмерная величина, это два. Скалярное произведение измеряется в м^2, тогда и координаты измеряются в м (ведь скалярное произведение находят как сумму произведений координат попарно). Как найти косинус — не сказано, это три. Например, можно косинус определять через ряды. Или берут гиперболический косинус в псевдоевклидовом пространстве.

Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю.

Короче, главное — скалярное произведение. Длины и углы вторичны.

В математике не используют единицы измерения, и радиан тут ничем не примечателен — такой же «безразмерный», как и длина, скалярное произведение или производная.

1 рад = $ {frac {360^{circ }}{2pi }}approx 57{,}295779513^{circ }approx 57^{circ }17’44{,}806»$ (мнемоническое правило запоминания в градусах-минутах-секундах: «Число радиана и порядок шутя пишу наизусть»

Опять из википедии, немного ниже:

При рассмотрении тригонометрических функций в математическом анализе всегда считается, что аргумент выражен в радианах, что упрощает запись; при этом само обозначение рад (rad) часто опускается.

Опускается — значит, размерность есть, просто не пишется.