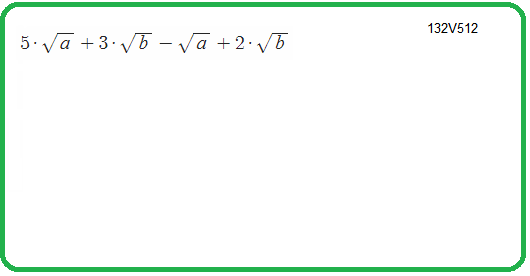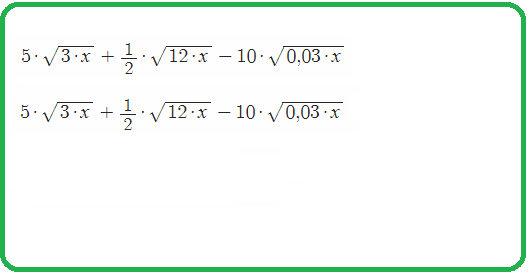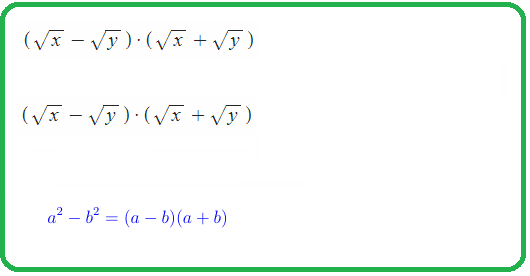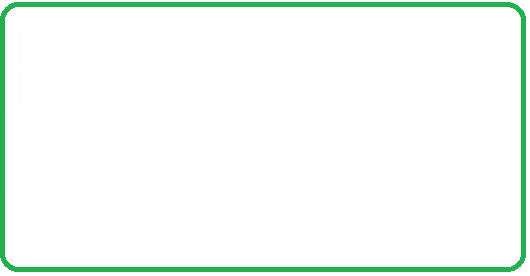Как найти радикал числа - Исправление недочетов и поиск решений вместе с Examum.ru

Что такое радикал?

Что такое радикал из числа? $sqrt{2}$ ? Это такое положительное число, квадрат которого равняется $2$ .

Основное тождество: $sqrt{a}$ — это неотрицательное число , чей квадрат $left(sqrt{a}right)^2=a$ , равен подрадикальному $a$.

проб Вот почему $sqrt{49}=7$ , потому что $7^2$ равен $49$ .
аналогично: $sqrt{x^6}=x^3$ $Leftrightarrow $ потому что $x^3$ в квадрате равен $x^6$.
Кстати, $sqrt{2}$ реально довольно «некрасивое» , очень длинное число $1,4142135624…. $
гораздо удобнее сказать «радикал из 2» или «корень из 2». И это число приблизительно $sqrt{2}approx1,41$
радикал — это математическая операция, обратная инверсия возведения в квадрат!
А вот $sqrt{2}cdotsqrt{8}$ вполне «приличное» число $4$. Потому что и произведение $sqrt{2}cdotsqrt{8}$ и число $4$ в квадрате дают $16$.
т.е. оба есть $sqrt{16}$ — «радикал из $16$» или «корень квадратный из 16».

Внимание! Квадратный корень существует только от неотрицательного числа, $age0$ и сам корень неотрицательный $sqrt{a}ge0$ .

Свойства радикалов:

$left(sqrt{a}right)^2=a$ ; $sqrt{a^2}=a$ — основные тождества . $sqrt{9}ne-3$

$sqrt{acdot b}=sqrt{a}cdotsqrt{b}$ — радикал произведения. $sqrt{frac{a}{b}}=frac{sqrt{a}}{sqrt{b}}$ — радикал деления.

$sqrt{a^2cdot b}=acdotsqrt{b}$     — вынос квадратного множителя за знак радикала,     частичное извлечение корня               $sqrt{frac{a}{b^2}}=frac{sqrt{a}}{b}$

$frac{1}{sqrt{a}}=frac{sqrt{a}}{a}$                   — избавление     знаменателя    от радикала

$frac{1}{a-sqrt{b}}=frac{a+sqrt{b}}{a^2-b}$ ; $frac{1}{a+sqrt{b}}=frac{a-sqrt{b}}{a^2-b}$ — умножение на сопряженное, избавление от радикала в знаменателе.

пробел

Вычисления, преобразования

Пример 1: Вычислить, преобразовать выражения, содержащие числовые радикалы:

1) $sqrt{729}=27$

потому, что $27$ именно то единственное положительное число, чей квадрат равен $729$;

2) $sqrt{75}=sqrt{3cdot25}=sqrt{3}cdotsqrt{25}=5sqrt{3}$

под корнем разложили на множители, увидели полный квадрат числа, извлекли;

3) $sqrt{2^2cdot3cdot7^2cdot6}=2cdot7cdotsqrt{3cdot3cdot2}=2cdot7cdot3cdotsqrt{2}=42sqrt{2}$

вынос корня по частям от множителей — полных квадратов; Числа без квадратов «выходят» вперед.

4) $frac{2}{sqrt{3}}=frac{2cdotsqrt{3}}{sqrt{3}cdotsqrt{3}}=frac{2sqrt{3}}{3}$

умножили числитель и знаменатель на радикал, дробь не изменилась. используем $sqrt{3}cdotsqrt{3}=3$;

5) $sqrt{48}cdotsqrt{12}cdotsqrt{75}=sqrt{48cdot12cdot75}=sqrt{8cdot6cdot2cdot6cdot3cdot25}=6cdot5cdotsqrt{16cdot3}=120sqrt{3}$

в конце вынос квадрата за знак; «если внутри квадрата два одинаковых множителя, из двух выносим один вперед».

6) $frac{1}{sqrt{3}-2}=frac{1cdotleft(sqrt{3}+2right)}{left(sqrt{3}-2right)cdotleft(sqrt{3}+2right)}=frac{sqrt{3}+2}{3-2^2}=-sqrt{3}-2$

избавили знаменатель от радикала, умножили на сопряженное и числитель, и знаменатель… упростили разность квадратов;

7) $sqrt{0.81}=sqrt{frac{81}{100}}=frac{sqrt{81}}{sqrt{100}}=frac{9}{10}=0.9$

десятичное число превратили в дробное , использовали свойство радикала от деления;

$sqrt{frac{64}{225}}=frac{sqrt{64}}{sqrt{225}}=frac{8}{15}$

свойство радикала от деления. нашли дробь, квадрат которой будет подрадикальной дробью.

Полезные Навыки работы с радикалами:

«Вынос квадрата за радикал» — если внутри радикала есть множитель — квадрат числа, то само число выносится вперед радикала.
Если внутри радикала есть два одинаковых множителя (квадрат?), то множителем впереди радикала выносим один из них.
Если в знаменателе дроби множителем является число с радикалом, то «для избавления» умножаем и числитель и знаменатель на радикал.
Если в знаменателе сложный радикал (сумма, разность), то «для избавления» умножаем и числитель и знаменатель на сопряженное!
Примечание: сопряженным к сумме называется разность, и наоборот. Например, сопряженные $a+sqrt{b}$ и $a-sqrt{b}$

Упрощения выражений с радикалами

Пример 2: Упростить радикальные выражения, используя свойства, формулы:

1) $sqrt{5a}-frac{1}{4}sqrt{80a}+20sqrt{0,05a}=sqrt{5a}-frac{1}{4}sqrt{16cdot5a}+20sqrt{frac{5}{100}cdot a}=sqrt{5a}-frac{1}{4}cdot4cdotsqrt{5a}+20cdotfrac{1}{10}cdotsqrt{5cdot a}=2sqrt{5a}$

разложение на множители под радикалом , вынос полного квадрата, группирование подобных $sqrt{5a}$;

2) $3sqrt{5}-sqrt{20}+sqrt{80}=3sqrt{5}-sqrt{4cdot 5}+sqrt{16cdot 5}=3sqrt{5}-2sqrt{5}+4sqrt{5}=left(3-2+4right)cdot sqrt{5}=5sqrt{5}$

вынос квадратного множителя из-под радикала, группирование подобных ;

3) $sqrt{5b}-2sqrt{20b}-3sqrt{80b}=sqrt{5b}-2cdot2cdotsqrt{5b}-3cdot4cdotsqrt{5b}=left(1-4-12right)cdotsqrt{5b}=-15sqrt{5b}$

частичный вынос за радикал, группирование подобных ;

4) $left(5sqrt{x}-2sqrt{3y}right)left(3sqrt{x}+sqrt{3y}right)=15x+5sqrt{3xy}-6sqrt{3xy}-2cdot3y=15x-sqrt{3xy}-6y$

отрытие скобок, умножение радикалов, группирование подобных.

5) $left(sqrt{x}-sqrt{2y}right)cdotsqrt{2xy}=sqrt{x}cdotsqrt{2xy}-sqrt{2y}cdotsqrt{2xy}=sqrt{x}cdotsqrt{x}cdotsqrt{2y}-sqrt{2y}cdotsqrt{2y}cdotsqrt{x}=xsqrt{2y}-2ysqrt{x}$

открытие скобок, умножение радикалов, свойство произведения $sqrt{acdot bcdot ccdot x}=sqrt{a}cdotsqrt{b}cdotsqrt{c}cdotsqrt{x}$ ;

6) $left(3sqrt{m}-4sqrt{2n}right)left(3sqrt{m}+4sqrt{2n}right)=left(3sqrt{m}right)^2-left(4sqrt{2n}right)^2=3^2cdot m-16cdot2n=9m-32n$

формула разности квадратов, свойство $left(asqrt{x}right)^2=asqrt{x}cdot asqrt{x}=a^2x$ ; $left(5sqrt{3y}right)^2=25cdotleft(sqrt{3y}right)^2$

7) $left(2sqrt{5}-7sqrt{2}right)left(3sqrt{2}+4sqrt{5}right)=2sqrt{5}cdot3sqrt{2}+2cdot5cdot4-7cdot2cdot3-7sqrt{2}cdot4sqrt{5}=6sqrt{10}+40-42-28sqrt{10}=-2-22sqrt{10}$

ф-ла разности квадратов, $7sqrt{2}cdot3sqrt{2}=7cdot3cdotsqrt{2}cdotsqrt{2}$ , группирование $17sqrt{a}-7sqrt{a}=10sqrt{a}$;

$left(3sqrt{a}-sqrt{c}right)^2=left(3sqrt{a}right)^2-2cdot3sqrt{a}cdotsqrt{c}+left(sqrt{c}right)^2=9a-6sqrt{ac}+c$

применили формулу сокращенного умножения.

пробел

Интерактивная доска:

Упражнения:

Источник

В данной статье речь пойдет об одной из самых фундаментальных гипотез теории чисел, споры о доказательстве которой не утихают и по сей день. Впрочем, обо всем по порядку.

abc-гипотеза была сформулирована независимо друг от друга математиками Дэвидом Массером в 1985 и Джозефом Эстерле в 1988 годах. Для понимания ее сути будет достаточно представлений об элементарной теории чисел, которые мы напомним ниже.

Итак, сначала несколько определений.

Простое число – натуральное число, которое имеет ровно два различных натуральных делителя – единицу и себя.

Радикалом числа называется число, равное произведению различных простых делителей целого числа. Здесь же следует отметить, что согласно основной теореме арифметики, любое натуральное число можно единственным образом представить в виде произведения простых множителей в каких-то степенях, поэтому радикал есть произведение этих самых простых множителей, взятых в первых степенях.

Взаимно простыми называются числа, наибольший общий делитель которых равен единице.

Возможно, понятие радикала числа покажется кому-то непривычным, но ситуация станет более знакомой, если мы вспомним, что радикал – это синоним арифметического корня (от лат. radix – корень).

Теперь рассмотрим тройки взаимно простых чисел a, b и c таких, что a + b = c, причем, не теряя общности, мы можем рассматривать тройки a, b и c, расположенные по возрастанию, а также радикал их произведения rad(abc).

abc-гипотеза говорит о том, что тройки, для которых выполняется неравенство

встречаются в некотором смысле реже.

Иначе можно сказать, что трудно найти такие взаимно простые числа, разложение которых содержит высокие степени, и разложение суммы этих чисел также содержит высокие степени.

Приведем пару примеров, а затем сделаем формулировку более строгой.

Пусть a = 64, b = 81, c = a + b = 64 + 81 = 145

rad(abc) = rad(64 ∙ 81 ∙ 145) =
= rad(2⁶ ∙ 3⁴ ∙ 5 ∙ 29) = 2 ∙ 3 ∙ 5 ∙ 29 = 870

145 < 870, то есть c < rad(abc)

Пусть a =5, b = 27, c = a + b = 5 + 27 = 32

rad(abc) = rad(5 ∙ 27 ∙ 32) = rad(5 ∙ 3³ ∙ 2⁵) = 5 ∙ 3 ∙ 2 = 30
32 > 30, то есть c > rad(abc)

rad(abc) = rad(5 ∙ 27 ∙ 32) =
= rad(5 ∙ 3³ ∙ 2⁵) = 5 ∙ 3 ∙ 2 = 30

32 > 30, то есть c > rad(abc)

Тройки второго типа считаются исключительными.

Численные методы позволили подсчитать количество таких троек в определенных пределах. Оказалось, что для c < 100 таких троек всего 6, для c < 1000 – 31, а для c < 1000000 – 1268.

Строгая формулировка abc-гипотезы говорит как раз о количестве таких исключительных троек, а также о том, насколько больше может быть число c.

В этом виде гипотеза прямо утверждает, что сумма чисел, являющихся произведением простых в больших степенях не может быть произведением простых чисел в больших степенях.

Существуют и другие, эквивалентные формулировки гипотезы – в частности, такая:

Так почему же именно эта гипотеза о том, каким будет разложение на простые множители суммы взаимно простых чисел, интересует современных математиков?

Дело в том, что с момента формулировки самой abc-гипотезы математики успели свести к ней множество нерешенных задач теории чисел и даже уже доказанную иным путем Великую теорему Ферма.

А для степеней, больших 6, справедливость ВТФ при условии справедливости abc-гипотезы можно показать так.

Множество других гипотез и теорем теории чисел, доказательства которых сводятся к abc-гипотезе настолько велико, что выходит за рамки данной статьи.

В 2012 году японский математик Синъити Мотидзуки опубликовал в интернете серию работ, по его словам, доказывающих abc-гипотезу. Камнем преткновения для математического сообщества стал объем доказательства (более 500 страниц), а также то, что автор объединил несколько кажущихся несочетаемыми областей математики, например, представляя арифметическую теорию пространств Тейхмюллера, которые были до этого сугубо геометрическим объектом. При этом Мотидзуки начинает с того, что переводит задачу в область эллиптических кривых, выполняя тот же переход, что и Эндрю Уайлс в доказательстве Великой Теоремы Ферма.

В результате, гипотеза сводится к доказательству неравенства между двумя величинами, связанными с эллиптическими кривыми.

Однако Мотидзуки идет дальше и переводит это неравенство в другую форму. Именно это является критическим моментом в доказательстве, споры о котором не утихают.

На данный момент доказательство опубликовано в научном журнале Publications of the Research Institute for Mathematical Sciences (RIMS), однако математическим сообществом оно пока не принято.

В заключение предложим читателю следующее рассуждение, иллюстрирующее фундаментальность abc-гипотезы.

Каждому из нас из младших и средних классов школы знакомо множество натуральных чисел, операции сложения и умножения, простые числа и разложение на простые множители. (В скобках заметим, что начала теории чисел изучают в средних классах, а вот продолжить изучение можно на старших курсах математических факультетов университетов, что само по себе намекает на простоту формулировок и исключительную сложность доказательств.)

Так вот с точки зрения операции сложения, любое натуральное число есть сумма некоторого количества единиц. А с точки зрения операции умножения, согласно основной теореме арифметики, любое натуральное число есть произведение простых множителей. Именно тогда, когда мы пытаемся понять, как сложение и умножение влияют друг на друга, и начинаются трудности.

Например, до сих пор не доказанные гипотезы Гольдбаха о представимости натурального числа в виде суммы простых или предмет данной статьи – abc-гипотеза.

Таким образом, доказательство abc-гипотезы может открыть нам некую фундаментальную структуру чисел. Согласитесь, настолько важный результат стоит многолетних проверок его доказательства.

Есть вопросы по материалу?

Вы можете задать их в нашем специальном чате. Мы поможем разобраться в теме лучше

Понравилась статья?

Источник

From Wikipedia, the free encyclopedia

In number theory, the radical of a positive integer n is defined as the product of the distinct prime numbers dividing n. Each prime factor of n occurs exactly once as a factor of this product:

${displaystyle displaystyle mathrm {rad} (n)=prod _{scriptstyle pmid n atop p{text{ prime}}}p}$

The radical plays a central role in the statement of the abc conjecture.^[1]

Examples[edit]

Radical numbers for the first few positive integers are

1, 2, 3, 2, 5, 6, 7, 2, 3, 10, 11, 6, 13, 14, 15, 2, 17, 6, 19, 10, 21, 22, 23, 6, 5, 26, 3, 14, 29, 30, 31, 2, 33, 34, 35, 6, 37, 38, 39, 10, 41, 42, 43, 22, 15, 46, 47, 6, 7, 10, … (sequence A007947 in the OEIS).

For example,

${displaystyle 504=2^{3}cdot 3^{2}cdot 7}$

and therefore

Properties[edit]

The function is multiplicative (but not completely multiplicative).

The radical of any integer is the largest square-free divisor of and so also described as the square-free kernel of .^[2] There is no known polynomial-time algorithm for computing the square-free part of an integer.^[3]

The definition is generalized to the largest -free divisor of , ${mathrm {rad}}_{t}$ , which are multiplicative functions which act on prime powers as

${displaystyle mathrm {rad} _{t}(p^{e})=p^{mathrm {min} (e,t-1)}}$

The cases and t=4 are tabulated in OEIS: A007948 and OEIS: A058035.

The notion of the radical occurs in the abc conjecture, which states that, for any , there exists a finite ${displaystyle K_{varepsilon }}$ such that, for all triples of coprime positive integers , , and satisfying a+b=c ,^[1]

${displaystyle c<K_{varepsilon },operatorname {rad} (abc)^{1+varepsilon }}$

For any integer , the nilpotent elements of the finite ring are all of the multiples of .

References[edit]

^ ^a ^b Gowers, Timothy (2008). «V.1 The ABC Conjecture». The Princeton Companion to Mathematics. Princeton University Press. p. 681.
^ Sloane, N. J. A. (ed.). «Sequence A007947». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Adleman, Leonard M.; McCurley, Kevin S. «Open Problems in Number Theoretic Complexity, II». Algorithmic Number Theory: First International Symposium, ANTS-I Ithaca, NY, USA, May 6–9, 1994, Proceedings. Lecture Notes in Computer Science. Vol. 877. Springer. pp. 291–322. CiteSeerX 10.1.1.48.4877. doi:10.1007/3-540-58691-1_70. MR 1322733.

Источник

Как вычислить радикалы вручную Квадратный корень из 34 равен 5. …

Содержание

Что такое радикал 12?
Что такое квадратный корень из 7?
Что такое правило радикалов?
Можно ли вычитать радикалы?
Каковы свойства радикалов?
Является ли 36 совершенным квадратом?
Как вычислять радикалы на калькуляторе?
Какова простейшая форма числа Ві в€љ 24?
Какова радикальная форма числа 1?
Как работают радикалы?

Рекомендую! Смотрите здесь: Как открыть счет в KRA в 2023.

Что такое радикал 12?

Что такое правило радикала «2в€љ3 Квадратный корень из 12 представлен в радикальной форме как в€љ12, что равно 2в€љ3. Поскольку 2в€љ3 нельзя упростить, такие корни называются сурдами. «.

Рекомендую! Узнайте больше на странице: Как работает бойлер для чайников в 2023.

Что такое квадратный корень из 7?

Какие корни из в€љ 4 » 2. Таким образом, квадратный корень из 7 в€љ7 приблизительно равен 2. «.

Рекомендую! Прочитайте тут: Что делать, если наушники Bluetooth не подключаются в 2023.

Что такое правило радикалов?

Какова простейшая форма Ві в€љ 24 «Правила радикалов Если n — целое положительное число больше 1, а a и b — положительные действительные числа, то 1. Обратное свойство. Nв€љ an = a, если n нечетное или. Nв€љ an = | a | если n четное. «.

Рекомендую! Узнайте тут: Сможете ли вы разбить авокадо в 2023.

Можно ли вычитать радикалы?

Что такое радикальная форма в математике » Радикалы могут быть упрощены путем сложения и вычитания, но вы должны помнить, что иногда вы не можете «»чисто»» упростить квадратные корни до числа. Первое, что следует отметить, это то, что радикалы можно складывать и вычитать только в том случае, если они имеют одинаковое число корней. «.

Рекомендую! Подробнее в обзоре: Какова формула гармоники в 2023.

Каковы свойства радикалов?

Каковы 3 закона радикалов «Упрощенная радикальная форма Все экспоненты в радикале должны быть меньше индекса. Все экспоненты в радикале не могут иметь общих коэффициентов с индексом. Под радикалом не должно быть дробей. В знаменателе дроби нет радикалов. «.

Является ли 36 совершенным квадратом?

Чему равен квадрат в€љ 1 » Неформально: Когда вы умножаете целое число (вЂњцелоевЂќ число, положительное отрицательное или ноль) на само себя, полученное произведение называется квадратным числом, совершенным квадратом или просто вЂњ квадратом. ВЂќ Так, 0 1 4 9 16 25 36 49 64 81 100 121 144 и так далее — это все квадратные числа. «.

Как вычислять радикалы на калькуляторе?

Как вычислить радикалы от руки.

Какова простейшая форма числа Ві в€љ 24?

Как можно упростить радикалы Это действительное решение уравнения x3 = 24. Кубический корень из 24 выражается как в€’24 или 2 в€’3 в радикальной форме и как (24)в…» или (24)0. Кубический корень из 24. Что такое кубический корень из 24 3. Является ли кубический корень из 24 иррациональным 4. Вопросы и ответы о кубическом корне из 24 Еще 1 ряд.

Какова радикальная форма числа 1?

Каковы свойства радикалов Каково значение квадратного корня из 1 Квадратный корень из 1 равен 1. …

Как работают радикалы?

Какая простейшая форма Ві в€љ 24 «Радикал или корень — это математическая противоположность экспоненты в том же смысле, в каком сложение противоположно вычитанию. Наименьшим радикалом является квадратный корень, обозначаемый символом в€љ. Следующий радикал — кубический корень, представленный символом Вів€љ. «.

Источник

В этом году исполнилось 350 лет со дня смерти Пьера де Ферма — одного из известнейших математиков прошлого. Ферма считается одним из создателей нескольких разделов математики: аналитической геометрии, математического анализа, теории вероятностей и теории чисел. К теории чисел можно отнести и знаменитую Великую теорему Ферма, которую он сформулировал в виде комментария на полях «Арифметики» Диофанта: «Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.» В «формульном» виде это выглядит так:

Для любого натурального n > 2 у уравнения aⁿ + bⁿ = cⁿ нет ненулевых решений в целых числах a, b, c.

За три с лишним века, прошедших со времен Ферма, математика сильно развилась и изменилась. Возникло много новых разделов и направлений, а счет новым идеям и методам уже давно никто не ведет. Даже теорему Ферма доказали уже почти 20 лет назад (это сделал Эндрю Уайлс в 1995 году). Но, как это довольно часто случается, между разными понятиями и теориями, даже если их разделяет несколько веков, можно обнаружить неожиданные взаимосвязи. Увидеть маленький пример такой связи — неожиданный подход к теореме Ферма — позволит эта задача. Нам потребуется одно несложное определение.

Радикалом натурального числа n (обозначается rad(n)) называется произведение всех простых делителей числа n, взятых по одному разу. Например, rad(100) = 10, rad(7) = 7, а rad(48) = 6.

Задача

Существуют ли такие три попарно взаимно простых натуральных числа A, B, C, что A + B = C и при этом C > 1000·rad(A·B·C)?

Подсказка

Такие числа существуют.

Что делает операция взятия радикала с числом? Если в разложении числа на простые множители какие-то из множителей встречаются в высоких степенях, то эта операция сильно уменьшит такое число: ведь после нее каждый из таких множителей останется только в первой степени. Поэтому если удачно подобрать A, B и C и в каждом из этих чисел будут множители в высоких степенях, то rad(A·B·C) будет во много раз меньше произведения A·B·C и может оказаться меньше сомножителей. Так, что даже умножение на 1000 не спасет.

Если сразу подобрать такие числа не получается, то можно попробовать вместо 1000 взять коэффициент поменьше. Например, 10. Также, чтобы не возиться с взаимной простотой, можно положить B = 1. Это сразу обеспечит требуемую в условии попарную взаимную простоту всех трех чисел (подумайте, почему).

Решение

Следуя совету из подсказки, будем считать, что B = 1. Тогда C = A + B = A + 1. Поскольку разность двух чисел делится на любой общий делитель этих двух чисел, а у нас получилось, что C − A = 1, то числа A и C взаимно просты.

Пусть пока коэффициент перед радикалом равен 10. Попробуем найти такие числа A и C, что А + 1 = С и C > 10·rad(A·C). Будем действовать «методом тыка».

Пусть С = 100. Тогда А = 99, rad(A·C) = 330, 10·rad(A·C) = 3300. Не совсем то, что хочется. За таким выбором С никаких глубоких соображений не стоит, просто автору показалось, что удобно взять степень 10, так как справа стоит множитель 10. Попробуем взять С = 1000. Тогда А = 999, rad(A·C) = 1110, 10·rad(A·C) = 11 100. Уже лучше!

Что будет, если продолжать пробовать в качестве С брать всё более высокие степени 10? Кое-что про это понять довольно легко. Так как А и С взаимно просты, то

rad(A·C) = rad(A)·rad(C) = 10·rad(A).

Значит, нужно попробовать подобрать такое С = 10ⁿ (то есть, фактически, надо подобрать подходящее n), чтобы выполнялось rad(A) < C/100 = 10ⁿ^− 2.

Заметим, что А — это число вида 9…9, в записи которого стоит ровно n девяток. То есть А делится на 9: А = 9·1…1 = 3²·1…1 (оба раза там по n единиц). Квадрат тройки в разложении уже есть. Можно ли еще увеличить степень тройки и сделать так, чтобы этот множитель из одних единиц тоже делился на 3? Можно. Более того, для любого натурального показателя степени k существует число такого вида, которое делится на 3^k. Чуть ниже докажем это, но сначала поймем, чем же это хорошо. А вот чем: радикал все эти степени тройки «уничтожит» и оставит только первую, то есть такое число от взятия радикала уменьшается во много раз. Но А чуть меньше С, поэтому если rad(A) меньше А хотя бы в 100 раз, то дело в шляпе, ведь тогда будет верна вся цепочка неравенств rad(A) < А/100 < C/100, а это нам и нужно.

Итак, нужно доказать, что для любого натурального k есть число вида 1…1, которое делится на 3^k. Докажем по индукции, что число из 3^k единиц подходит.

База индукции, k = 1. Нетрудно проверить, что 111 делится на 3. Шаг индукции: предположим, что число из 3^k единиц делится на 3^k, и покажем, что из этого следует, что число из 3^k^+ 1 единиц делится на 3^k^+ 1. Дело в том, что число из 3^k^+ 1 единиц — это три «блока» из 3^k единиц, то есть его можно разложить на множители:

Первый множитель делится на 3^k по нашему предположению, а второй делится на 3 по признаку делимости на 3, значит всё произведение делится на 3^k^+ 1. Что и требовалось доказать.

Из доказанного только что утверждения получается, что число из 3⁴ = 81 единиц делится на 81. Значит, если взять в качестве А число из 81 девятки, то оно будет делиться на 81·9 = 3⁶ = 729. Поэтому rad(A) меньше такого А как минимум в 3⁵ = 243 раза. И оно нам подходит. Наверняка это не самый маленький возможный пример. Но из него очень легко получить ответ на исходную задачу, в которой перед радикалом стоял коэффициент 1000 (а не 10): нужно просто взять такое k, что 3^k^+ 1 больше 10 000 (а не 100), то есть k = 8 подойдет (3⁸ = 6561, 3⁹ = 19 683). Тогда, аналогично тому, что было чуть выше, получим, что число А из 3⁸ девяток будет делиться на 3¹⁰, а его радикал будет как минимум в 3⁹ раз меньше. То есть верны неравенства

А значит,

Ясно, что есть и другие примеры подходящих чисел. Наверняка можно подобрать гораздо меньшие числа. Но данный способ решения ценен тем, что в нем видны все этапы рассуждений: от «экспериментальных» данных через обобщение и формулировку гипотезы к полному решению, которое годится для любого коэффициента перед радикалом в правой части неравенства из условия.

Послесловие

Рассмотренная задача напоминает формулировку abc-гипотезы — не доказанного еще утверждения из теории чисел, которое было сформулировано в середине 1980-х годов. Вот формулировка этой гипотезы:

Для любого ε > 0 существует константа k такая, что для любых попарно взаимно простых натуральных чисел A, B, C с условием A + B = C верно неравенство С < k·rad(A·B·C)^1 + ε.

Из решения нашей задачи видно, что если в правой части неравенства взять первую степень радикала (то есть при ε = 0), то сразу окажется бесконечно много троек чисел A, B, C, которые нарушают это неравенство. А вот если ε > 0, то такого «раздолья» уже не будет: для каждого ε можно подобрать такую константу k (для разных ε константы будут разные), что какую бы мы не взяли тройку натуральных чисел, удовлетворяющих равенству A + B = C, для них обязательно будет выполняться указанное неравенство. Если, конечно, гипотеза верна. Верна она или нет — сейчас неизвестно. Пока никому не удалось ни доказать ее, ни опровергнуть.

Попытки доказать abc-гипотезу регулярно предпринимаются, но пока все тщетно. Последней, видимо, серьезной заявкой на успех было доказательство японского математика Синъити Мотидзуки, однако представленные им тексты настолько трудны для понимания даже ведущими специалистами, что, вероятно, в ближайшее время никто не сможет проверить, верно ли его доказательство или нет. Ну, а раз математическому сообществу проверить не удается, то это фактически означает, что доказательства нет. «The Paradox of the Proof» — не отягощенный серьезными математическими подробностями рассказ об этом всем (есть неплохой русский перевод этого текста).

Есть два довода в пользу того, что гипотеза верна. Оба они ни в коем случае не могут рассматриваться как серьезные аргументы — скорее, эти доводы вселяют слабую надежду в справедливость гипотезы. Первый — большое количество компьютерных вычислений по поиску связанных с гипотезой троек чисел. Ищут тройки, для которых ε был бы как можно больше, но пока даже значение ε = 0,7 не достигнуто. Кстати, каждый может поучаствовать в этом.

Второй довод в пользу справедливости гипотезы состоит в том, что из нее следуют многие очень сложные и глубокие теоремы и еще не доказанные гипотезы. Достаточно упомянуть лишь гипотезу Морделла (которую в 1983 году доказал Фальтингс, за что он получил Филдсовскую медаль). Подробнее об этом можно узнать из лекции Д. Орлова «АВС-гипотеза и ее следствия».

Доступность формулировки гипотезы чем-то напоминает историю с Великой теоремой Ферма, формулировка которой тоже понятна школьнику. Правда, в остальном эти утверждения скорее противоположны. Дело тут не в том, одно из них уже доказанная теорема, а про второе пока ничего не понятно. Важно значение для развития науки и тот способ, которым это значение достигается. Теорема Ферма несколько веков была притягательной задачей для многих ученых. В попытках ее доказать родилось много плодотворных идей и методов. А доказана она была с использованием мощнейшего аппарата алгебраической геометрии, который был создан в XX веке (подробнее об этом читайте в статье Ю. Соловьева «Гипотеза Таниямы и последняя теорема Ферма», а вся история этой теоремы изложена в книге С. Сингха «Великая теорема Ферма»). Но вот из самой теоремы Ферма никаких полезных следствий нет. В противоположность этому из abc-гипотезы, как уже говорилось, следует много важных и не очень фактов. В том числе — что если abc-гипотеза верна, то из нее буквально в несколько предложений следует Великая теорема Ферма. Вот как это получается.

Будем доказывать теорему Ферма при n > 6 (при меньших n она была доказана больше двухсот лет назад; более того, в середине XIX века Куммер доказал теорему Ферма при всех n, меньших 100, кроме значений 37, 59, 67), используя abc-гипотезу с ε = 1. Считается, что в этом случае k = 1. Доказываем от противного. Пусть такая тройка ненулевых взаимно простых чисел x, y, z существует: xⁿ + yⁿ = zⁿ. Если обозначить A = xⁿ, B = yⁿ, C = zⁿ, то эти три числа удовлетворяют условию abc-гипотезы. Значит, верно, что C < rad(A·B·C)². Но

rad(A·B·C) = rad(xⁿ·yⁿ·zⁿ) = rad(x·y·z) < x·y·z < z³,

так как очевидно, что z больше x и y. Получается, что zⁿ = C < rad(A·B·C)² < (z³)² = z⁶. Противоречие, ведь n > 6.

Вот такое вот простое и понятное доказательство теоремы Ферма. Вряд ли француз имел в виду это доказательство в своем комментарии в книге Диофанта. Но мы можем теперь сказать, что почти знаем поистине чудесное доказательство этой теоремы, которое вполне можно уместить на полях… Осталось только доказать abc-гипотезу.

Рассмотренная задача предлагалась участникам LXXVII Московской математической олимпиады.

Источник