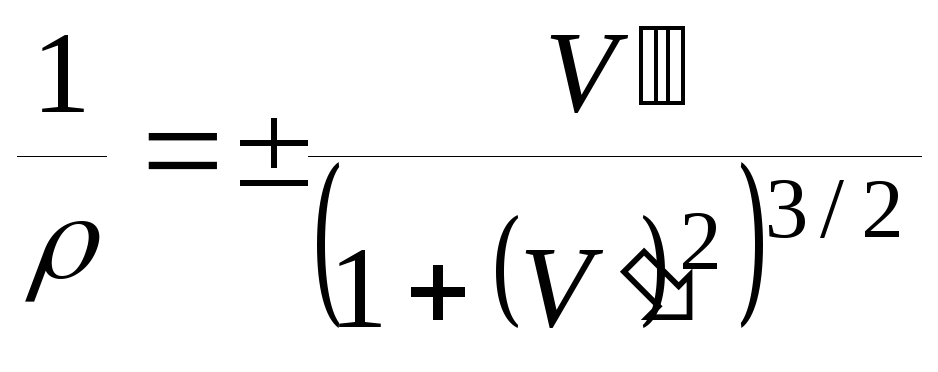Калькулятор для расчета длины балки и длины изогнутой балки.
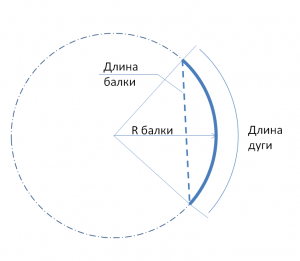
По длине балки и её радиусу высчитывает длину дуги. И наоборот по длине дуги и радису высчитывает длину балки.
Мне лично понадобилось когда пришли чертежи с длинной дуги и радиусом балки. И надо было создать по ним модель в Текле.
По длине балки (хорда) и радиусу находим длину изогнутой балки.
Длина изогнутой балки:
___
Обратная задача, по известной длине дуги и радиусу узнаем длину балки (хорда) которую необходимо построить чтобы получить изогнутую балку заданной длины при данном радиусе.
Длина балки
___
Исходя из этих гипотез, найдем величину удлинения какого-либо волокна балки при чистом изгибе. Положим, что два близких поперечных сечения балки (рис. 99) повернулись одно относительно другого на угол Лф. Радиус кривизны нейтрального слоя балки, или ее изогнутой оси, обозначим р, а длину волокна, лежащего в нейтральном слое между рассматриваемыми сечениями, — s. Расстояния у условимся считать положительными в сторону выпуклости и отрицательными в сторону вогнутости. Абсолютное удлинение рассматриваемого волокна As = Sj — s, а относительное удлинение [c.108]
Радиус кривизны нейтрального слоя балки, или, что то же, ее изогнутой оси, обозначим р, а длину волокна, лежащего в нейтральном слое между рассматриваемыми сечениями, х. [c.199]
Найдем, исходя из этих гипотез, величину удлинения какого-либо волокна балки при чистом изгибе. Положим, что два близких поперечных сечения балки (рис. 146) повернулись одно относительно другого на угол Дф. Радиус кривизны нейтрального слоя балки, или, что то же, ее изогнутой оси, обозначим р, а длину волокна, лежащего в нейтральном слое между рассматриваемыми сечениями, 8. [c.233]
При = 1 10 /сг/ с.и и J—230 M определить радиус кривизны изогнутой оси балки и величину изгибающего момента. [c.156]
Величина, обратная радиусу кривизны в какой-либо точке кривой, называется ее кривизной. Следовательно, формула (86) связывает кривизну нейтрального слоя, а значит кривизну изогнутой оси балки, с величиной изгибающего момента М и жесткостью сечения балки У, относительно нейтральной оси. [c.110]
Рассмотрим элемент этого продольного волокна, расположенный между двумя плоскостями и и имеющий до деформации длину , а после деформации — длину х -Ь Ах. Обозначим через Л радиус кривизны изогнутой оси балки. Из рисунка 128, 6, где рассматриваемый элемент волокна и элемент нейтральной оси изображены в более крупном масштабе, легко увидеть, что [c.382]
На рис. 11.2 изображены для примера два различных радиу-са местной кривизны изогнутой оси балки, рассмотренной ранее на рис. 11.1. Здесь большему изгибаюш,ему моменту отвечает большая кривизна (меньший радиус кривизны). [c.188]
Обозначим кривизну в плоскости ху через %у= 1ру, где рг,— радиус кривизны, а в плоскости хг через Хг=1/рг. Кривизна будет положительна, когда форма изогнутой в плоскости ху балки такова, что она обращена вогнутостью вниз, т. е. в сторону положительного направления оси у. Точно так же и кривизна Пг считается положительной, когда изогнутая в плоскости хг балка об- [c.313]
Величина, обратная радиусу кривизны в какой-либо точке кривой, называется ее кривизной. Следовательно, формула (86) связывает кривизну нейтрального слоя, а значит кривизну изогнутой оси балки, со значением изгибающего момента М и жесткостью сечения балки относительно нейтральной оси. Жесткость сечения пропорциональна модулю упругости и осевому моменту инерции иными словами, она определяется материалом, формой и размерами поперечного сечения, [c.107]
Двумя поперечными сечениями 1—1 и 2—2 вырежем из балки этого участка элемент длиной dz и представим его в более крупном масштабе (рис. 85, а—г). После изгиба торцы балки несколько наклонятся, образуя угол dB- Обозначим радиус кривизны изогнутой оси балки р, а длину одного из продольных волокон, лежащих в нейтральном слое, — тп. Так как эти волокна не изменяют своей длины при изгибе, можно написать [c.119]
В данной задаче единственным отличным от нуля напряжением будет изгибающее напряжение Он. В упругом ядре внутри балки (— о < Ха< а) имеет место равенство Оц = ец = Ех Я, где Н — радиус кривизны изогнутой оси балки, а Е — модуль Юнга. В пластической зоне ап = а у- Таким образом, [c.270]
Для определенного сечения радиус кривизны изогнутой оси балки р есть величина постоянная, и поэтому относительное удлинение волокна прямо пропорционально расстоянию этого волокна до нейтральной оси балки. [c.233]
Иногда знак плюс или минус в уравнении (10.5) приписывают радиусу кривизны, который считают положительным, если он направлен от изогнутой оси балки к центру кривизны и совпа- [c.268]
Рассмотрим теперь особые сечения балки, в которых изгибающий момент обращается в нуль, а радиус кривизны — в бесконечность. Кривизна изогнутой оси балки в таких сечениях равна нулю. Такие точки изогнутой оси балки, в которых радиус кривизны принимает бесконечные значения, а изгибающий момент обращается в нуль, на-зывают точками перегиба. [c.269]
Швейцарский ученый Яков Бернулли (1654—1705) применил дифференциальное исчисление к выводу формулы радиуса кривизны кривой и получил зависимость между кривизной изогнутой оси балки и изгибающим моментом [c.558]
При чистом изгибе балки постоянного сечения изгибающие моменты и жесткости сечений EJ постоянны по ее длине. В этом случае радиус р кривизны изогнутой оси балки имеет постоянное значение [см. выражение (7.16), т. е. балка изгибается по дуге окружности]. [c.247]
Балка пролетом 1 м, свободно лежащая на двух шарнирных опорах, изогнута по дуге окружности. Сечение балки прямоугольное 00 сторонами Ь = 6 ом и Н = 4 ом. Прогиб, измеренный посередине пролета, оказался равным / = 6,25 мм. Определить ве,личину модуля упругости материала балтет и радиус кривизны оси при уоловот , что наибольшее напряжете в балке равно О =10 МПа. [c.75]
Так как радиус кривизны изогнутой оси балки R —величина постоянная, то из полученного равенства видим, что относительное удлинение Sy (или укорочение волокна прямо пропорционально его расстоянию от нейгрального слоя. [c.304]
Радиус нейтральной оси изогнутой балки с учетом эксцентриситета между осями Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Дизайн машины ↺ | |
| Дизайн машины | Проектирование элементов машин ↺ | |
| Проектирование элементов машин | Расчет против статической нагрузки ↺ | |
| Расчет против статической нагрузки | Проектирование криволинейных балок ↺ | |
| Проектирование криволинейных балок | Радиус волокна и оси ↺ |
|
✖Радиус центральной оси — это радиус оси криволинейного луча, проходящей через центральную точку.ⓘ Радиус центральной оси [R] |
+10% -10% |
||
|
✖Эксцентриситет между центральной и нейтральной осью — это расстояние между центральной и нейтральной осью криволинейного конструктивного элемента.ⓘ Эксцентриситет между центральной и нейтральной осью [e] |
+10% -10% |
|
✖Радиус нейтральной оси — это радиус оси криволинейной балки, проходящей через точки, в которых нет напряжения.ⓘ Радиус нейтральной оси изогнутой балки с учетом эксцентриситета между осями [RN] |
⎘ копия |
Радиус нейтральной оси изогнутой балки с учетом эксцентриситета между осями Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Радиус центральной оси: 80 Миллиметр —> 0.08 метр (Проверьте преобразование здесь)
Эксцентриситет между центральной и нейтральной осью: 6.5 Миллиметр —> 0.0065 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.0735 метр —>73.5 Миллиметр (Проверьте преобразование здесь)
Кредиты

Институт технологий и науки Шри Говиндрама Сексариа
(СГСИТС),
Индор
Саурабх Патил создал этот калькулятор и еще 700+!

Национальный Технологический Институт
(NIT),
Хамирпур
Аншика Арья проверил этот калькулятор и еще 2700+!
16 Радиус волокна и оси Калькуляторы
Радиус нейтральной оси изогнутой балки с учетом эксцентриситета между осями формула
Радиус нейтральной оси = Радиус центральной оси—Эксцентриситет между центральной и нейтральной осью
RN = R—e
В прошлой части мы обсудили, как может изменяться момент стержня и как выяснить, не разрушится ли он под действием нормальных и касательных сил. Однако под воздействием момента стержни могут изгибаться и изменять форму, что может приводить к неправильной работе конструкций или даже их разрушению в процессе эксплуатации. Сегодняшняя статья посвящена вопросу нахождения прогибов и углов наклона при изгибе.
Уравнение кривой
В прошлой части мы выяснили, что для нахождения момента нам необходимо знать какой у дуги изгиба радиус кривизны, какой у сечения статический момент и какой модуль Юнга у материала балки:
Затем мы устранили из уравнения такое значение как радиус кривизны, из наших уравнений, так как нас не столько волновало, как под воздействием изменится балка, сколько не сломается ли она.
Однако сейчас нас интересует именно то, как будет деталь изгибаться под воздействием моментов, как будет меняться геометрия .
В прошлый раз мы не заостряли внимание на вопросе «что такое радиус кривизны», да и просто «что такое кривизна». В этой части мы данную проблему решим, а также объясним как это значение поможет нам в сопромате вычислить деформации изгиба.
Фактически, до этого момента мы оперировали не столько радиусом, сколько кривизной, которая обратно пропорциональна радиусу:
А сейчас мы поговорим о том, какое значение она имеет с точки зрения геометрии.
Если нет желания смотреть, как с точки зрения математики выводятся геометрические характеристики, можно промотать до следующего жирного шрифта и принять за данность выводы.
Кривизна – это то, насколько сильно изменяется угол наклона касательной к нашей кривой за единицу длины дуги.

Так как любую кривую можно представить как сумму бесконечно малых дуг, принадлежащих разным окружностям, стоит посмотреть, на сколько будет изменяться угол в двух точках ее дуги.

Углы будем измерять в радианах (180°=π, 360°=2π). Длина окружности равна удвоенному произведению радиуса на π: l=2πR. Круг — фигура симметричная, и поэтому в любой точке кривизна будет одинакова и равна:
χ=frac{2π}{2π*R}=frac{1}{R}
Вот так и находилась формула кривизны балки. И теперь мы хотим поставить её на службу поиска формы балки.
Нам нужно найти изменение угла за бесконечно малый пройденный путь, и мы имеем некоторую функцию. При этом её первая производная будет равна тангенсу угла с осью x, которую мы обозначим греческой тета θ:

Нам же для вычисления кривизны необходимо найти изменение угла θ:
Гуглим таблицу дифференциалов, находим, что дифференциал от тангенса равен следующему выражению:
d(arctg (x))=frac{dx}{1+x^2}
Так как функция сложная (y’ — тоже какая-то функция, пусть нам и не известная), получившееся значение надо будет домножить на производную от аргумента:
dθ=frac{dx}{(1+(y’)²)}*y’’
Кривизна же — это изменение угла за пренебрежительно малый отрезок длины:
Уравнение угла наклона нам известно. Теперь нам нужно вычислить длину малой дуги. Достаточно малой, чтобы можно было пренебречь кривизной и считать её прямой. Тогда мы сможем воспользоваться теоремой Пифагора:
Где dx – пройденный путь по оси x, а dy – по оси y.
Нам для красоты уравнения хотелось бы избавиться побыстрее от дифференциалов, чтобы в формуле остались только производные. Для этого мы делим все, что было под корнем на (dx)^2:
frac{(dx)^2}{(dx)^2}+frac{(dy)^2}{(dx)^2}=1+(y')^2
Так как (dx)^2/(dx)^2=1, а (dy)/(dx) – это производная y по x.
Чтобы уравновесить данное вмешательство, мы должны домножить все выражение на dx (т.к. √(dx)^2=dx):
Теперь у нас есть все для нахождения кривизны:
χ=frac{dθ}{dl}=frac{dx}{(1+(y’)^2)}*y’’*frac{1}{dxsqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^2}
*frac{1}{sqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^{{3}}}
Отсюда стоит читать всем, даже тем, кому математика вывода кривизны не очень интересна.
Итак, мы смогли вычислить чему равна функция кривизны:
χ=frac{1}{R}=frac{y’’}{(sqrt{1+(y’)^2})^{3}}
Где y – прогиб (т.е. расстояние на которое выше или ниже окажется определенная точка балки, по сравнению с недоформированным состоянием), y’ – первая производная от неё, а y» – вторая (или кривизна).
Перед нами же стоит задача вычислить форму. Так как в сопротивлении материалов прогибы достаточно небольшие, изменением длины можно пренебречь. Следовательно, нам остается лишь вычислить изменение координаты y в зависимости от x. И в полученной формуле нам мешает это сделать очень объемный знаменатель (√(1+(y’)²)³.
Если подумать логически, то так как прогибы в сопромате достаточно небольшие, можно было бы не учитывать производную y’, так как она является отношением катетов треугольника, который бы получился опусти мы к оси x перпендикуляр.
Дело в том, что даже если прогиб (координата y) будет составлять 1/10 от x, производная в самом крайнем углу будет чуть больше 0,2x. А ее квадрат 0,04x. А (√(1+(y’)²)³ около 1,06.
Это не назвать пренебрежительно малым значением, однако его проще компенсировать коэффициентами запаса прочности. Да и прогиб этот слишком большой для основ сопротивления материалов (большими деформациями занимается отдельная дисциплина). Вот демонстрация прогиба в натуральном соотношении:
В результате, если мы проигнорируем знаменатель, получим формулу, которую уже можно будет использовать в дальнейших расчетах:
χ=θ’=y’’
Угол поворота и прогиб
Мы уже выяснили, что кривизна балки в каждой части зависит от момента, возникающего в этом сечении, статического момента и модуля Юнга материала, из которого это балка сделана:
Сегодня же мы будем решать обратную задачу и находить изгиб балки. В первой части статьи мы выяснили, что для малых изгибов радиус кривизны (он равен единице деленной на радиус кривизны) практически равен второй производной от прогиба (насколько по оси z поднимется или опустится балка в конкретной точке). В итоге мы, зная как распределяется момент, сможем посчитать вторую производную прогиба для каждой точки балки:
y’’=χ=frac{1}{R}=frac{M_z}{I_z×E}
Нам же интересна форма балки: углы её наклона и на сколько сантиметров выше или ниже она окажется.
Начнём с наклона. Как мы уже выяснили, первая производная будет равна тангенсу наклона. Тангенс равен отношению противолежащего катета к прилежащему:

Углы наклона у нас будут маленькими, поэтому прилежащий катет будет практически равен радиусу. Отношение противолежащей стороны к радиусу является синусом:

А синус малого угла, как мы уже выяснили вначале статьи, численно равен углу в радианах.
Примечание: мы выяснили, что для малых углов тангенс, синус и угол численно равны. Эта закономерность важна не только в сопромате, но и в большинстве других инженерных наук. Например, в геодезии, при определении величины малых скатов.

Как следствие, для того, чтобы найти угол наклона, нам необходимо проинтегрировать кривизну:
θ=∫y''dx=∫frac{M_z*dx}{J_z*E}=frac{1}{J_z*E}∫M_z*dx=y'+C
Углы и прогибы балки под воздействием момента
В простейшем случае к балке приложен только момент:

В таком случае значение момента является константой. Обозначим ее как M. Тогда найти прогиб можно по формуле:
θ=∫y''dx=frac{1}{I_z*E}∫M_z*dx=frac{M_z*x}{I_z*E}+C
Остается найти константу интегрирования. Так как в начале координат балка жестко закреплена, угол в месте закрепления будет равен нулю, как следствие, константа тоже будет равна нулю. Эпюра угла наклона будет выглядеть вот так:

Для того, чтобы найти прогибы надо, соответственно, проинтегрировать получившееся выражение еще раз:
y=∫θdx=∫frac{M_z*x*dx}{I_z*E}+∫Cdx=frac{M_z*x^2*dx}{2*I_z*E}+Cx+D
Константу C мы уже знаем, а константу D можно найти по той же логике: балка жестко закреплена в начальной точке, а значит прогиб y в ней будет равен 0. А полученная нами формула приводит к нулю в начале координат только при нулевой константе:
(M*0)2/2+C*0+D=0, только если D=0
Ну а эпюра прогибов будет выглядеть следующим образом:

Углы и прогибы балки под воздействием силы
В случае же, если момент появляется под воздействием силы, эпюры как бы сдвигаются на одну вперед:

Линейной станет функция момента, а угол будет постепенно увеличиваться (вначале быстро, потом медленнее, так как момент будет меньше).
Mz=P(l-x), где Mz— момент возникающий в балке в точке, которая расположена на расстоянии x от места закрепления балки, а l – длина балки.
Получили мы это уравнение следующим образом: мы знаем что в месте закрепления возникает момент который компенсирует момент от воздействия силы на конце балки:
Также в месте закрепления будет возникать сила, которая будет компенсировать силу внешнюю:
Когда мы будет отдаляться от точки закрепления на величину x, сила реакции опоры будет создавать для нашего сечения момент MRa=Ra*x. Он будет складываться с моментом передавшимся с начала балки:
M_z=M_{z_{0}}-M_{R_{a}}=\=p*l+R_a*x=P*l-P*x=\=P(l-x)
Зная функцию распределения момента мы можем найти функции наклона и прогиба.
Наклон будет увеличиваться по параболе:
θ=∫frac{(P*(l-x))*dx}{I_z*E}=frac{P*(l-x)^2}{2*I_z*E}+C

Ну а прогиб будет изменяться уже по кубическому закону:
y=∫frac{P*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{P*(l-x)^3*dx}{6*I_z*E}+C*x+D
Примечание: если проще, то l-x потому, что в нулевой координате момент равен расстоянию до силы, а затем уменьшается на то расстояние, которое мы до нее прошли

Углы и прогибы балки под воздействием равномерно-распределенной нагрузки
В случае с равномерно-распределенной нагрузкой ситуация абсолютно аналогична: эпюры «сдвигаются» на одну относительно воздействия силы. Поперечная сила изменяется по линейному закону Qy=Ra-qx=ql-qx=q(l-x), момент по параболе Mz=q(l-x)2/2:

Угол наклона, соответственно, будет определяться кубической функцией:
θ=∫frac{q*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{q*(l-x)^3*dx}{6*I_z*E}+C

А прогиб уже функцией четвёртой степени:
y=∫frac{q*(l-x)^3*dx}{6*I_z*E}=\=frac{q*(l-x)^4*dx}{24*I_z*E}+Cx+D

Расчет балки на прогибы и углы наклона. Метод начальных параметров. Пример
На практике достаточно редко случается ситуация, при которой на конструкцию действует только одна сила, а сама конструкция состоит из одной балки, закрепленной только в одном месте. Разберем как пример расчёт балки, в которой есть все виды воздействий:

Примечание: среди внешних воздействий отсутствует сила. Мы сделали это для того, чтобы не загружать статью лишними расчётами: сила реакции опоры в расчетах ничем не отличается от силы внешней.
Первым делом, нужно заменить места закрепления на силы, которые они создают для поддержания равновесия балки. В данном случае это две вертикальные силы (моментов шарнирные опоры не создают):
Теперь наша задача найти эти силы. Сделать это довольно просто: составляем уравнение сил по оси y и момента для точки закрепления балки.
Уравнение равновесия сил по оси Y:
R_a-ql+R_b=R_a-30+R_b=0, R_a+R_b=30
Уравнение равновесия момента в левой точке закрепления:
M_a=ql*a+frac{15l^2}{2}+M-d*R_b=30+30-10-5R_b=0
Где a — расстояние до начала действия равномерно-распределенной нагрузки, d — расстояние до опоры b.
Из уравнения момента мы можем найти, чему равна сила реакции правой опоры:
Подставляем это значение в уравнение равновесия сил и получаем силу реакции первой опоры:
R_a+R_b=R_a+14=30, R_a=16

Для того, чтобы найти прогибы, нам надо составить уравнения момента для каждого участка. В нашем случае удобнее всего Теперь найдём функцию распределения момента для первого участия. Так как в точке a балка закреплена не жестко, момент в ней по условию равен нулю. В ней возникает только сила реакции опоры Ra=16.
Момент на первом участке будет зависеть от удаления от этой силы:

Для нахождения угла наклона это выражение надо проинтегрировать:
θ_{(I)}=frac{1}{I_zE}∫R_axdx=frac{R_ax^2}{2I_zE}+C
И ещё раз для получения прогиба:
y_{(I)}=frac{1}{I_zE}∫frac{R_ax^2dx}{2}+∫Cdx=frac{R_ax^3}{6I_zE}+Cx+D
Затем нам нужно найти геометрию балки на участке с равномерно-распределенной нагрузкой.

При этом, момент на этом участке будет зависеть от двух составляющих: от силы реакции Ra с первого участка и от нагрузки q.
M_{z_{(II)}}=f(R_a,x)+f(q,x)
Функция момента (Mz(I)=Ra*x=12x) возникающего от силы на первом участке будет справедлива и для нашего участка: момент по-прежнему будет равен произведению плеча на силу.
По мере того, как мы будем отступать от начала действия равномерно-распределенной нагрузки, момент будет увеличиваться по квадратичному закону (почему, можно прочитать в статье посвященной теореме Журавского) M(q)=qx’^2/2, где x’ — расстояние от начала приложения нагрузки.
Нам удобнее все расчёты проводить из одной точки, поэтому для второго участка x’=x-a, где a координата начала приложения нагрузки. Таким образом, уравнение момента на втором участке будет выглядеть так:
Mz_{(II)}=Ra*x-frac{q(x-a)^2}2=16x-frac{15(x-1)^2}2
Интегрируем чтобы найти наклон:
θ_{(II)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6)+C
И ещё раз, чтобы найти прогиб:
y_{(II)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32})
На следующем участке действие равномерно-распределенной нагрузки заканчивается. При этом, мы хотим чтобы q(x-a)2/2 в формуле осталась: всё-таки она вносит вклад в момент и геометрию стержня.
Чтобы эту небольшую проблему исправить, мысленно продолжим распределенную силу до конца конструкции, но приложим в противовес ей точно такую же, направленную в другую сторону:

Таким образом на следующий участок стержня (который начинается в точке b) дополнительно будет приложена распределенная нагрузка q, которая будет создавать момент M=q(b-x)2/2.
Суммарный момент для третьего участка будет равен:
Mz_{(III)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2
Ну и, соответственно, найти наклон и прогибы не составляет трудности:
θ_{(III)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6)+C
y_{(III)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32})+Cx+D
Четвёртый участок начинается в месте приложения момента и заканчивается на второй опоре.
Составляем уравнение момента:
Mz_{(IV)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2+10
Где c — расстояние от начала координат до места приложения момента, а x-c, расстояние между точкой, которую мы рассматриваем и местом приложения момента. В нулевой степени это выражение всегда равно единице, поэтому для уравнения момента это константа. Но после интегрирования это выражение становится важной частью уравнения наклона:
θ_{(IV)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))+C
А затем и уравнения прогиба:
y_{(IV)}=\frac{1}{Iz*E}∫(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32}+frac{M(x-c)^2}{2})+Cx+D

Остается вычислить константы интегрирования. На первой и последней опоре прогибы (т.е. вертикальные перемещения) будут равны нулю. Подставляем x=0 в уравнение первого отрезка:
y_{(I)}=frac{R_a0^3}{6I_zE}+C*0+D
И выясняем, что константа интегрирования D равна нулю.
Подставляя константу интегрирования D в уравнение последнего участка для закрепленного конца балки (т.е. x=l=5) мы получим следующее уравнение:
0=frac{1}{Iz*E}*(frac{16*5^3}6-frac{15(5-1)^4}{32}+frac{15(5-3)^4}{32}+frac{10(5-4)^2}{2})+С*5+0
Выражение равно нулю по причине того, что прогибы в месте закрепления образовываться никак не могут.
Решив уравнение мы получим значение второй константы интегрирования:
С=frac{225,83}{5*Iz*E}=frac{45,17}{Iz*E}
Дальше остается лишь подставить эти константы в уравнения и мы получим уравнения наклонов и прогибов.

Итак, мы выяснили по каким законам будет прогибаться каждый участок балки.
Если резюмировать, то для получения уклона и прогиба на некотором участке, нам нужно просуммировать все воздействия и их проинтегрировать.
Метод начальных параметров
В общем виде углы наклона будут считаться так:
А прогибы так:
Примечание: не забывайте компенсировать равномерно-распределенную нагрузку в точке, где она заканчиваться!
На практике гораздо целесообразнее считать момент, наклон и прогиб сразу для всей балки, с помощью трех систем уравнений: системы моментов, наклонов и прогибов.
Уравнения моментов для каждого участка
Так их удобнее составлять, так как достаточно просто для каждого нового участка добавлять воздействия:
Уравнения наклонов
Как можно заметить, для того, чтобы из системы уравнений моментов получить систему уравнений наклонов достаточно проинтегрировать каждый член и добавить константу интегрирования C:
Уравнения прогибов
Как ни странно, для того, чтобы их получить, достаточно проинтегрировать каждый из членов уравнения наклона, добавить ещё одну константу интегрирования D, а первую константу C умножить на x.
Итак, подошёл к концу разговор о том, как материалы противодействуют изгибам. В прошлых частях мы уже выяснили, какие нормальные напряжения возникают в материале при попытке его согнуть. Обсудили и как с распределением момента связаны поперечные силы и касательные напряжения. А сейчас выяснили и как будет материал менять свою форму под воздействием изгиба.
Это имеет далекоидущие последствия для всех инженерных дисциплин и опирающихся на них специальностей. Например, ротор турбин, являющийся по своей сути длинным стержнем на опорах, под силой тяжести достаточно сильно изгибается. По этой причине для всех турбин большой мощности противопоказан быстрый старт. Перед тем, как соединять статор и ротор, стержень турбины необходимо повращать, чтобы он избавился от изгибающих деформаций. Иначе лопатки будут цепляться и в лучшем случае деформироваться, а в худшем ломаться. Но это уже совсем другая история.
В следующей части мы поговорим о другом виде воздействия момента на стержень: о кручении.
Автор: К.А.Овчинников
Редактор: Сабуров Даниил
Эксперт: Ершов Марк
За консультативную поддержку по математической части огромная благодарность Гришиной Ольге Андреевне, старшему преподавателю кафедры высшей математики БГТУ ВОЕНМЕХ.
Информация о произведении:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Источники:
- Горбатовский Александр Александрович Дифференциальное уравнение изогнутой оси балки // Курс лекций по сопротивлению материалов МГТУ ИМ. Н.Э.БАУМАНА
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Лекции по сопротивлению материалов в БГТУ «ВОЕНМЕХ» им. Устинова
- http://mathhelpplanet.com/static.php?p=krivizna-ploskoi-krivoi
- https://spravochnick.ru/matematika/krivizna_krivoy/krivizna_i_ee_vychislenie/
- iSopromat Метод начальных параметров. Расчет перемещений сечений балки // https://youtu.be/xRp-ViFUl7Y
4 143
Определение деформации балок при изгибе
Прогиб и поворот
сечения балки
При действии
внешних сил, расположенных в одной из
главных плоскостей инерции сечения
балки, наблюдается искривление ее оси
в той же плоскости, происходит плоский
изгиб.
|
|
На |
Перемещение
ц.т. сечения по направлению, перпендикулярному
к оси балки, называетсяпрогибом
балки в этом
сечении. Прогиб
обозначается буквой
.
=
При деформации
балки сечение поворачивается на некоторый
угол
,
который называетсяуглом
поворота сечения.
Обе величины,
определяющие деформации балки, являются
функцией от
.
Уравнение
представляет
собой уравнение кривой, по которой
изогнется ось балки, это будетуравнение
изогнутой оси балки.
Касательная к
изогнутой оси балки в т.
составит с осью
угол, равный
.
С другой стороны, тангенс угла,
образованного касательной к кривойи осью
,
как известно, равен
Так как на практике
прогибы балки обычно малы по сравнению
с длиной балки, то углы
малы.
Для таких углов
можно считать, что тангенс угла равен
самому углу, выраженному в радианах.
Следовательно
(5.19)
|
При выбранных |
Дифференциальное
уравнение изогнутой оси балки
Для получения
зависимости
надо установить, как зависят деформации
балки от внешних сил, изгибающих ее, от
размеров и материала балки.
Такая зависимость
была получена нами ранее при выводе
формулы нормальных напряжений при
изгибе в виде связи кривизны оси балки
с изгибающим моментом (5.11):
(а)
где
радиус кривизны изогнутой оси балки.
Однако в общем
случае использовать зависимость (а) для
определения прогибов не удается.
С другой стороны,
из курса высшей математики известна
зависимость между радиусом кривизны
плоской кривой и координатами
и
ее точек:
(б)
Приравнивая
выражения (а) и (б) исключим радиус
кривизны:
(в)
Это дифференциальное
уравнение изогнутой оси, или дифференциальное
уравнение упругой линии.
Выше мы уже отмечали,
что
– величины очень малые, поэтому их
квадратом можно пренебречь по сравнению
с единицей. Тогда уравнение (в) упростится
(г)
Это приближенное
дифференциальное уравнение изогнутой
оси. Правило знаков для изгибающего
момента
установлено ранее.
Знак в формуле (г)
зависит от выбора направлений осей
координат. В нашем случае, когда ось
горизонтальна и направлена вправо, а
осьвниз, надо брать знак «–». Итак
(5.20)
Если ось у
направлена вверх, надо взять знак «+».
Интегрирование
дифференциального уравнения упругой
линии
Для того, чтобы
получить аналитические выражения для
прогибов и углов поворота необходимо
найти решение дифференциального
уравнения (5.20). Правая часть уравнения
является известной функцией для каждой
конкретной балки с конкретным загружением.
Интегрируя его один раз, получим:
Это выражение
определяет закон изменения углов
поворота сечений балки.
После повторного
интегрирования найдем уравнение оси
балки
Постоянные
интегрирования С
и D
находятся из граничных условий.
Уравнения (5.20)
записываются для каждого участка балки
и интегрируются. При большом числе
участков определение const
и
осложняется, т.к. приходится решать
большое число совместных алгебраических
уравнений, из которых они вычисляются.
Поэтому для таких балок были разработаны
другие методы.
Один из таких
методов сводится к уравниванию однотипных
const
интегрирования, для чего, при составлении
аналитических выражений изгибающих
моментов
по участкам балки, необходимо соблюдать
ряд условий.
Метод уравнивания
произвольных постоянных
(метод Клебша)
Равенство между
собой произвольных постоянных (и
)
при большом числе участков балки возможно
при соблюдении следующих условий:
-
Отсчет координат
всех
участков должен вестись от одного конца
балки. -
Все составляющие
выражения
предыдущего участка, должны сохраняться
неизменными в выраженияхпоследующего участка. Поэтому, если на
каком-то участке появляется распределенная
нагрузка,
не идущая до конца балки, то ее надо
продлить до конца балки, добавив на
этих же участках такую же распределенную
нагрузку с противоположном знаком. -
Сосредоточенные
моменты
вводятся в виде
,
гдерасстояние от начала балки до сечения,
где приложены.
-
Интегрирование
дифференциальных уравнений должно
вестись без раскрытия скобок.
Поясним выполнение
перечисленных условий на примере:
Пример (рис.5.11):
Дано:
1,5м;
4,5м;
4м;
20кН;
45кН/м;
20кНм;
кН/см2;
=16кН/см2;
=10кН/см2;
Рис.5.11
На рис. 5.11 сплошными
линиями и перечеркнутыми показаны
нагрузки
заданные,
а пунктиром показаны добавки нагрузоксогласно п.2 метода Клебша. Сначала
учитываем только заданные нагрузки.
По правилам, показанным при решении
примера 1 на рис. 5.5, находим:
-
Из уравнений
равновесия всей балки при заданных
нагрузках находим все опорные реакции:
154,12кН;
84,12кН;
.
-
Строим эпюру
и эпюру
,
из которых находим105,68кНм
и
106,62кН
Для балки подберем
стандартный двутавр:
Из условия прочности
балки (5.17) находим
Соседние файлы в папке Лекции Мартышев В.П
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #