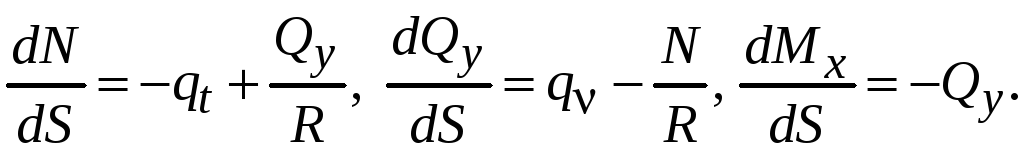140
12.1.
Краткие
сведения из теории
Брусья с криволинейной
осью различаются:
на брусья
большой кривизны,
если отношение
брусья малой
кривизны,
если отношение
где R
– радиус кривизны бруса; h
– высота поперечного сечения
(рис. 12.1).
Рис.
12.1
Расчётные формулы
для напряжений в случае прямого бруса
справедливы и к брусу малой кривизны.
При рассмотрении
бруса большой кривизны предполагается,
что:
-
кривой брус
является плоским (т.е. его ось является
плоской кривой); -
поперечное сечение
бруса симметрично относительно
плоскости, в которой расположена его
ось, а внешние силы действуют в этой
плоскости; -
поперечные сечения
бруса, плоские до деформации, остаются
плоскими и после деформации (гипотеза
плоских сечений); -
продольные
изогнутые волокна находятся в одноосном
напряжённом состоянии (давление
продольных волокон бруса друг на друга
не учитывается).
|
|
|
Рис. 12.2 |
Внутренние усилия в
поперечном сечении кривого бруса
определяются методом сечений и приводятся
к нормальной силе N,
поперечной силе
и изгибающему моменту
(рис. 12.2). Нормальная сила N
считается положительной, если она
вызывает растяжение, поперечная сила
положительная, если она вращает отсечённую
часть бруса относительно начала участка
по часовой стрелке; изгибающий момент
больше нуля, если он увеличивает кривизну
бруса (рис. 12.2). На эпюрах N,
и
положительные значения будем откладывать
перпендикулярно геометрической оси
бруса от центра его кривизны, а
отрицательные значения – к центру его
кривизны.
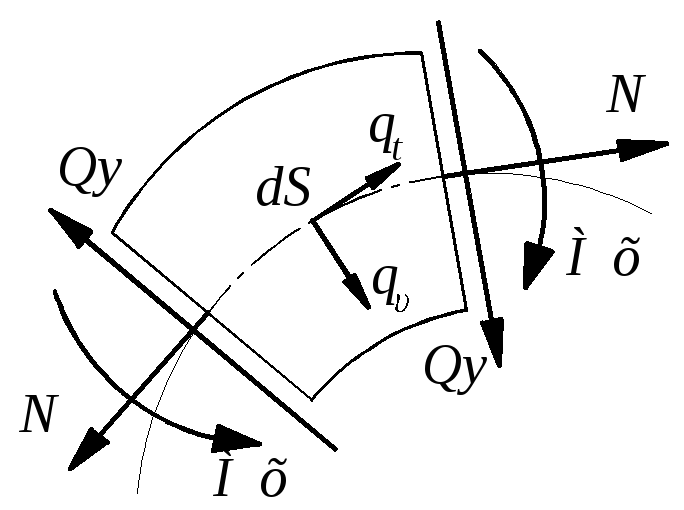
Для кривого бруса
дифференциальные зависимости между
внутренними силовыми факторами и внешней
нагрузкой имеют иную форму, чем для
прямолинейного. Рассмотрим элемент
кривого бруса с криволинейной осью
радиуса R
(рис. 12.3).
|
|
|
Рис. 12.3 |
Равнодействующая внешней
нагрузки q,
приложенная к элементу
,
даёт проекцию
на нормаль
и
на касательную
.
При переходе от сечения А
к сечению В
внутренние силовые факторы N,
и
изменяются и получают приращение dN,
и
.
В силу малости угла
(12.1)
Составим уравнения
равновесия для элемента АВ:
Учитывая соотношения
(12.1) и пренебрегая членами второго
порядка получим
При чистом изгибе
(,
)
нормальные напряжения
в поперечном сечении кривого бруса
находят по формуле
где
– изгибающий момент в сечении кривого
бруса; R
– радиус кривизны оси бруса; F
– площадь поперечного сечения; y
– расстояние от центральной оси сечения
(ось x)
до точки, где определяется напряжение;
– радиус кривизны нейтральной линии
(рис. 12.4).

12.4
При изгибе кривого
бруса нейтральная линия смещена по
отношению к геометрической оси бруса
к центру кривизны на величину
.
В частности для прямоугольного сечения
где
,
– радиусы кривизны соответственно
наружного и внутреннего волокна сечения;
h
– высота сечения;
Для других форм
поперечного сечения величина
приведена в соответствующих справочниках
и учебной литературе.
Если кривой брус
подвергается продольно-поперечному
изгибу, то в его поперечных сечениях
кроме изгибающего момента
возникают нормальная и перерезывающая
силы N
и
.
В этом случае нормальные напряжения
определяются по формуле
Перерезывающая
сила возникает за счёт касательных
напряжений
,
которые приближённо можно вычислить
по формуле Журавского.
11.2. Примеры
решения задач
№1.
Для бруса с криволинейной осью (рис.
12.5) построить эпюры внутренних силовых
факторов (N,
,
)
и найти нормальные напряжения в опасном
сечении бруса.
Отрезки, характеризующие величины М, N и Q в данном сечении, откладываются в принятом масштабе по направлениям, нормальным к оси бруса, т. е. по радиусам кривизны бруса. [c.311]
Если радиус кривизны бруса р>5Л. то расчет перемещений ведется по формуле [c.115]
В формулах через py- обозначен радиус кривизны бруса, при котором начинается образование пластических деформаций [c.272]
Работнова гипотеза старения 292 Работнова теория ползучести 292 Радиус кривизны брусьев остаточный [c.555]
Остаточный радиус кривизны бруса Рост определяется из выражения [c.275]
Если радиус кривизны бруса р>(2 —3)Л, то расчёт перемещений ведётся по формулам прямого бруса. [c.130]
Введе.м необходимые обозначения. Через ро (рис. 174, а) обозначим радиус кривизны оси бруса (линии центров тяжести сечений), а через Го — радиус кривизны нейтрального слоя. Величина Го пока не известна. В дальнейшем мы увиди.м, что Го всегда меньше ро и нейтральная линия для бруса большой кривизны смещена относительно центра тяжести в сторону центра кривизны. Ординату будем отсчитывать от нейтральной линии. [c.161]
Вынесенная за знак интеграла постоянная величина /р =0, поскольку радиус кривизны деформированного бруса не равен бесконечности. Следовательно, это равенство имеет смысл лишь при [c.213]
Кривой брус называют брусом малой кривизны, если радиус кривизны оси бруса р 7/1, где /г — размер поперечного сечения в плоскости кривизны. Напряжения при изгибе и кручении брусьев малой кривизны [c.231]
Обозначим радиус кривизны изогнутой оси бруса через р. Удлинение волокна АА будет равно разности длин дуг и 00 , но длина дуги ЛЛх = (р + у)й(б, а дуги ООх = рйв- Мы предположили, что нейтральный слой, а, следовательно, и ось бруса при [c.252]
Брусьями малой Кривизны считаются такие, для которых отношение радиуса кривизны их оси к высоте поперечного сечения не менее десяти (R/h> 10). [c.138]
В этом выражении М — изгибающий момент, действующий в рассматриваемом сечении, — 5 — статический момент сечения относительно нейтральной оси. Ко — радиус кривизны нейтрального слоя, у — координата площадки, отсчитываемая от нейтральной оси бруса, на которой определяются нормальные напряжения. [c.286]
Построение эпюры нормальных напряжений по высоте сечения бруса нужно начинать с определения радиуса кривизны Ко по нейтральному слою. [c.286]
Для бруса с трапециевидным сечением (рис. 16.3.2, а) радиус кривизны до нейтрального слоя находится из выражения [c.288]
JJ— радиус радиус кривизны нейтрального слоя кривого бруса коэффициент асимметрии цикла 5г. Sy, (S)—статические моменты площади фигуры относительно осей [c.7]
Нейтральная линия пп смещена по отношению к геометрической оси бруса к центру его кривизны на величину =р — г, где о — радиус кривизны геометрической оси бруса. [c.288]
Радиус кривизны нейтральной линии бруса для каждой формы его поперечного сечения устанавливают из выражения [c.288]
Пример 2.4. Кривой брус в виде четверти дуги окружности неподвижно закреплен концом Л и на конце В нагружен силой F. Радиус кривизны осевой линии / = 5 м (рис. 2.29). Построить эпюры продольных перерезывающих Qn сил и изгибающих моментов Мх, [c.46]
P = —m. Результат не записит от радиуса кривизны бруса. [c.464]
Принято различать брус малой и большой кривизны. Основным признаком для такого деления является отношение высоты сечения /г в плоскости кривизны к радиусу кривизны оси бруса ро. Если это огиошение существенно меньше единицы (/г/ро = 0,2 и меньше), считается, что брус имеет малую кривизну. Для бруса большой [c.160]
Значения радиуса кривизны г нейтральноге слоя при изгибе кривого бруса большой кривизны [c.232]
В ЭТОМ случае пластические деформации распределяются по всему сечению. При грубом приближении можно считать, что при гибке прямоугольного бруса с малым радиусом кривизны имеет место чистопластический изгиб с упрочнением. Момент внешних сил в этом случае при 117=0 равен [c.123]
Своеобразие напряженно-деформированного состояния кривых брусьев связано с тем, что, по определению, у таких брусьев высота h сравнима с радиусом кривизны осевой линии. Рассмотрим изгиб кривого бруса в плоскости Оуг (рис. 12.40), представляющей плоскость симметрии бруса. Ось Оу направим от центра кривизны бруса О, поместив начало отсчета в точке Oi на нейтральном слое О—0. Радиус кривизны линии О—О равен г. Примем гипотезу плоских сечений и рассмотрим поворот друг относительно друга двух близких сечений а—а и р—р, расстояние между которыми Asq по линии О—О связано с углом Аф соотношением Aso = гАф. При этом длина отрезка Aso по определению нейтрального слоя не изменяется при чистом изгибе. Длина отрезка ЬЬ As = (г + у) Аф при изгибе с изменением угла между сечениями аа и рр на величину бАф = б Аф + баАф изменяется и равна [c.282]
Принято различать брус малой и большой кривизны. Основным признаком для такого деления является отношение высоты сечения h в плоскости кривизны к радиусу кривизны оси бруса PQ. Если это отношение существенно меньше единицы h/pQ < 0,2), считается, что брус имеет малую кривизну. Для бруса большой кривизны отношение hfpQ соизмеримо с единицей. Таким образом, указанное деление является условным и не имеет четкой границы. [c.215]
ИЗ ВЕСТ ия
ТОМСКОГО ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ПОЛИТЕХНИЧЕСКОГО Том 75 ИНСТИТУТА им^ни С. М. КИРОВА 1954 г.
ОБ ОДНОМ СПОСОБЕ ОПРЕДЕЛЕНИЯ РАДИУСА
КРИВИЗНЫ НЕЙТРАЛЬНОГО СЛОЯ ПЛОСКИХ КРИВЫХ БРУСЬЕВ ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
м. г. пинский
Определение нормальных напряжений в поперечном сечении кривого ‘«бруса производят по приближенной формуле
Р М х
—(1)
г 5 /’о + г
где Р — растягивающая сила, /И— изгибающий момент, .Г — площадь поперечного сечения бруса,
5 — статический момент площади поперечного сечения относительно
нейтральной линии, г — расстояние рассматриваемой точки поперечного сечения, в которой определяется напряжение, отсчитываемое при положительном своем значении в сторону внешней дуги от н. л., г0 — радиус кривизны нейтрального слоя.
Величина л>, как известно, определяется в каждом частном случае по зависимости:
Т7
йР
(2)
Г
Если положить и = то
Г йР «7 И
(3)
Из (3) можно определить г0 для различных форм сечения [1] аналитически. Существует ряд приближенных способов определения [1], [2]. В этой заметке предлагается прием для подсчета знаменателя в выражении (3)
(4)
3 и
г
Прием этот заключается в следующем. Пусть мы имеем любое поперечное сечение плоского бруса (фиг. 1). Проведем линию аах на расстоянии и от оси кривизны бруса. На расстоянии йи проведем линию параллельную ааи тогда элементарная площадь
№ = 2ab.dii. (5)
Для подсчета интеграла (4) необходимо элементарную площадь йР (5) уменьшить в И. Для этого, сохранив ширину элементарной полоски, уменьшим высоту полоски, т. е. йЬ
dF
= 2
ab
du.
(6)
и и
Соединим точку а с точкой о и на расстоянии 1 см от оси кривизны про-
водим линию, параллельную искомой оси. Эта прямая пересекает ао в точке /. Рассматривая подобие треугольников аоЪ и foe, запишем соотношения
отсюда
ab =4
bo ео
ab ab
To и
(7)
Таким образом, из (6) на основании (7)
dF __ 2 abdu
2fe du.
и и
Сносим отрезок fe на прямую ab, при этом fe — a2b и
dF и
тогда
2 a2b.du.
(8)
Для подсчета интеграла (4) следует разбить поперечное сечение на несколько участков. Производя для каждого участка такое построение, получим ряд точек. Соединив эти точки плавной линией и просуммировав преобразованную таким образом площадь фигуры, мы тем самым подсчитаем графически интеграл (4).
J
_ CAIL J и
Fu
где /^х — преобразованная площадь (заштрихована, фиг. 2).
Определив обычным суммированием можно по (3) подсчитать
Го =
л
(9)
Подсчет этих площадей производится планиметром.
ля повышения точности подсчета можно ее просто увеличить, для чего Лрямук> следует отложить на п см. Тогда формула (9) будет иметь вид:
И
1
ЛИТЕРАТУРА
. Б е д я е в Н. М. Сопротивление материалов, 7-е изд., стр. 590—593, 1951. Тимошенко С. П. Сопротивление материалов, ч. И, стр. 73, 1946.