Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Величина и направление силы Лоренца определяются соотношением
где $vector$, $vector$ и $vector$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10 -31 кг — масса электрона, | кг |
| e | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
При больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя электронов me, а необходимо учитывать релятивистское увеличение массы.
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
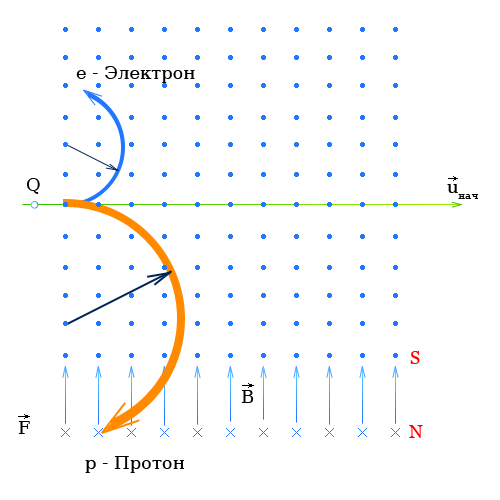
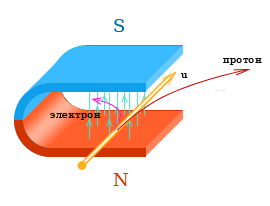
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10 -27 кг — масса протона, | кг |
| p | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Аналогично при больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя протонов mp, а необходимо учитывать релятивистское увеличение массы.
Радиус движения электрона по окружности
Электрон описывает в однородном магнитном поле окружность радиусом 4 мм. Скорость движения электрона равна 3,5 • 10^6м/с. Определите индукцию магнитного поля.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,857
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Шпаргалка по общей электронике и электротехнике.
5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
В некоторых электровакуумных приборах используется движение электронов в магнитном поле.
Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.
При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.
Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.
Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.
Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).
Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.
Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.
Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.
Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.
Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.
Радиус движения электрона по окружности
Электрон, ускоренный разностью потенциалов U = 1 кВ, влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Индукция магнитного поля В = 1,19 мкТл. Найти радиус R окружности, по которой движется электрон.
Дано:
U = 1 кВ = 10 3 В
В = 1,19 мкТл = 1,19 ·10 -6 Тл
Решение:
На электрон, движущейся в магнитном поле
действует сила Лоренца
,
которая является центростремительной
Т. к. движение электрона происходит по окружности, то
Радиус R окружности, по которой движется электрон, будет равен
Скорость электрона найдем из закона сохранения энергии
Ответ:
5.3. Движение заряда в однородном магнитном поле
Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)
Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле
Сила Лоренца FL, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем
следовательно, можем записать уравнение
из которого легко получить выражение для угловой скорости частицы
Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период
тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты
Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).
Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками
Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.
Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых
направлена вдоль поля, а вторая
перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью и вращения по окружности с угловой скоростью . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):
Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле
Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?
Решение. Из уравнений (5.11) находим угол между скоростью протона и полем
Кинетическая энергия протона будет
Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.
Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов
Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).
Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В
Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).
http://b4.cooksy.ru/articles/radius-dvizheniya-elektrona-po-okruzhnosti
http://online.mephi.ru/courses/physics/electricity/data/course/5/5.3.html
Классический радиус электрона
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 февраля 2015 года; проверки требуют 10 правок.
Класси́ческий ра́диус электро́на, также известный как радиус Лоренца или длина томсоновского рассеяния, базируется на классической релятивистской модели электрона, в которой предполагается, что вся масса электрона имеет электромагнитную природу, то есть масса электрона, умноженная на квадрат скорости света, равна энергии создаваемого им электрического поля. При этом электрон представляется сферической частицей с определённым радиусом, поскольку при нулевом радиусе энергия созданного электроном поля была бы бесконечной.
= 2,8179403267(27) ⋅10-15 м,
где e и m0 есть электрический заряд и масса электрона, c — скорость света, а 
Классический радиус электрона равен радиусу полой сферы, на которой равномерно распределён заряд, если этот заряд равен заряду электрона, а потенциальная энергия электростатического поля 
.
ДифференцированиеПравить
Классическая шкала длины радиуса электрона может быть мотивирована рассмотрением энергии, необходимой для сборки количества заряда в сферу заданного радиуса .
Электростатический потенциал на расстоянии от заряда равен
- .
Чтобы вывести дополнительное количество заряда из бесконечности, необходимо вложить в систему энергию которая равна
- .
Если «предполагается», что сфера имеет постоянную плотность заряда , то
- и .
Выполнение интегрирования для , начиная с нуля до конечного радиуса , приводит к выражению для суммарнаю энергии , необходимой для сборки полного заряда в однородную сферу радиуса :
- .
Это называется электростатической собственной энергией объекта. Заряд теперь интерпретируется как заряд электрона ; энергия устанавливается равной релятивистской масс-энергии электрона ; числовой коэффициент 3/5 игнорируется как специфический для частного случая однородной плотности заряда. Затем радиус «определяется» как классический радиус электрона и мы приходим к выражению приведенному выше.
Обратите внимание, что дифференцирование не говорит, что это фактический радиус электрона. Оно только устанавливает пространственную связь между электростатической собственной энергией и масштабом массы-энергии электрона.
Связь с другими фундаментальными длинамиПравить
Сегодня классический радиус электрона рассматривается как классический предел для размеров электрона, которая используется при рассмотрении нерелятивистского рассеяния Томсона, а также в релятивистской формуле Клейна — Нишины. Классический радиус электрона является представителем тройки фундаментальных длин; две другие из этой тройки — боровский радиус ( ) и комптоновская длина волны электрона
Учитывая постоянную тонкой структуры α, классический радиус электрона можно переписать в форме:
где — приведённая комптоновская длина волны электрона. Через длину классического радиуса электрона можно выразить комптоновскую длину волны электрона
и боровский радиус:
Если рассматривать радиус протона 0,8768 фемтометра(CODATA-2006) ,то радиус электрона в 3.21 раза больше радиуса протона.
Отсюда радиус электрона равен: 2,814528 фемтометра (2017-02-04)
Существование постоянной однако, не означает, что это настоящий радиус электрона. На таких расстояниях действуют законы квантовой механики, в которой электрон рассматривается как точечная частица.
ЛитератураПравить
- CODATA value for the classical electron radius Архивная копия от 10 января 2022 на Wayback Machine at NIST.
- Arthur N. Cox, Ed. «Allen’s Astrophysical Quantities», 4th Ed, Springer, 1999.
СсылкиПравить
- Length Scales in Physics: the Classical Electron Radius
Лучший ответ
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
[ е = — 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Сила Лоренца действующая на электрон и протон
Величина и направление силы Лоренца определяются соотношением
[ vector{F_{L}}= e vector{v} × vector{B} ]
где $vector{v}$, $vector{B}$ и $vector{F}$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
[ F_{L} = e v B ]
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины.
Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
Если
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10-31 кг — масса электрона, | кг |
| e | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
[ evB = frac{m_{e} v^{2}}{r} ]
и, следовательно,
[ r = frac{m_{e} v}{eB} ]
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
[ p = + 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Сила Лоренца действующая на протон
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
Если
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10-27 кг — масса протона, | кг |
| p | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
[ r = frac{m_{p} v}{p B} ]
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Сила Лоренца |
стр. 667 |
|---|
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.