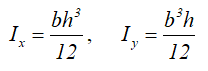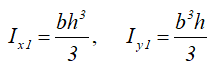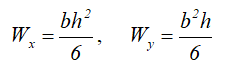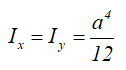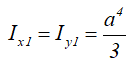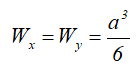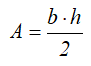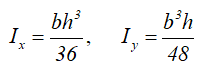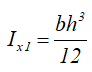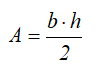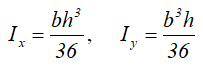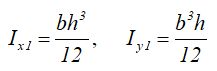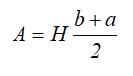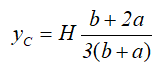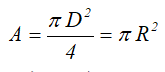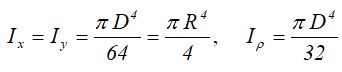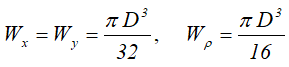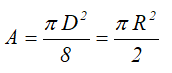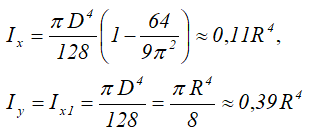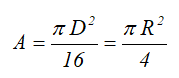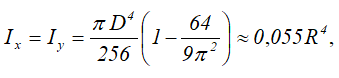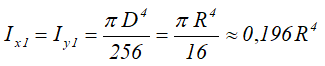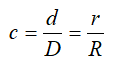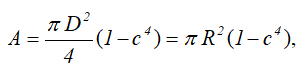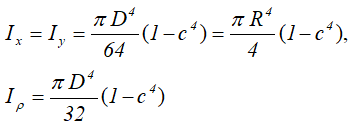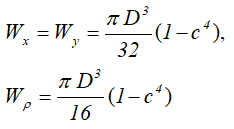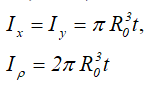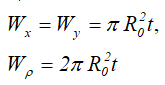Как найти радиус инерции трубы или кольца?
Радиус инерции трубы (кольца) относительно центральной оси z равен радиусу инерции относительно центральной оси y и рассчитывается по формуле:
iy = iz = D √(1+(d/D)2) /4 ,
где
iy — радиус инерции относительно центральной оси y в мм;
iz — радиус инерции относительно центральной оси z в мм;
D — наружный диаметр сечения в мм;
d — внутренний диаметр сечения в мм.
Момент сопротивления трубы или кольца (формула и расчет)
Момент инерции трубы или кольца (формула и расчет)
Моментом инерции
твердого тела относительно какой –
либо осиz
(осевым моментом инерции) называется
скалярная величина, равная сумме,
составленной из произведений массы mk
каждой точки тела на квадрат ее расстояния
rk
до данной оси.
Момент инерции
бесконечно тонкого кольца (материальной
окружности) относительно его оси вращения
равен произведению его массы на квадрат
радиуса:
Момент инерции
тела относительно оси представить в
виде произведения массы тела на квадрат
длины некоторого отрезка
,
называемого радиусом инерции тела
относительно соответствующей оси:
Под радиусом инерции
тела относительно какой – либо оси
можно понимать радиус такого бесконечно
тонкого кольца, в котором нужно
сосредоточить всю массу М тела, чтобы
получить момент инерции кольца, равный
моменту инерции тела относительно этой
оси.
10. Момент инерции относительно параллельных осей (теорема Гюйгенса — Штейна).
Момент инерции
тела относительно какой – либо оси
равен моменту инерции этого тела
относительно центральной оси, параллельной
данной оси, сложенному с произведением
массы тела на квадрат расстояния между
этими осями.
— теорема Гюйгенса
– Штейна.
11. Осевые моменты инерции однородных тел: стержень, полый и сплошной цилиндры, шар.
— момент инерции
тонкого прямого стержня постоянного
сечения
Момент инерции
однородного прямого тонкого стержня
относительно его центральной оси
симметрии равен 1/12 произведения массы
стержня на квадрат его длины.
— момент инерции
сплошного
круглого цилиндра.
Момент инерции
однородного сплошного круглого цилиндра
относительно его оси вращения равен
половине произведения массы цилиндра
на квадрат его радиуса.
— момент инерции
полого круглого цилиндра.
Момент инерции
однородного полого круглого цилиндра
относительно его оси вращения равен
половине произведения массы цилиндра
на сумму квадратов его наружного и
внутреннего радиусов.
12. Динамическое уравнение вращения твердого тела вокруг неподвижной оси.
(1), где
Произведение
момента инерции тела относительно его
оси вращения на угловое ускорение тела
равно главному моменту всех приложенных
к телу внешних сил относительно той же
оси.
Уравнение (1)
называется динамическим уравнением
вращательного движения твердого тела.
13. Теорема об изменении кинетической энергии материальной системы.
Изменение кинетической
энергии механической системы на некотором
перемещении равно сумме работ внешних
и внутренних сил, действующих на
материальные точки системы на этом
перемещении.
,
где Т – кинетическая энергия в конечный
момент времени
Т0
— кинетическая энергия в начальный
момент времени
∑Аiе
+∑Аij
– сумма работ внешних и внутренних сил
Условие: необходимо
начальное и конечное положения.
14. Кинетическая энергия материальной системы. Теорема Кенига.
Механическая
система – совокупность тел, связанных
между собой различными связями.
Положения и движение
каждого из тел взаимно обусловлено.
Кинетическая энергия механической
системы определяется как арифметическая
сумма кинетических энергий i-го
тела, входящего в систему.
Теорема Кенига:
Кинетическая
энергия механической системы равна
сумме кинетической энергии центра масс
системы, масса которого равна массе
всей системы, и кинетической энергии
этой системы в ее относительном движении
относительно центра масс.
Соседние файлы в папке Шпоры
- #
- #
- #
- #
- #
- #
Таблица. Изгиб. Осевые моменты инерции сечений (статические моменты сечений), осевые моменты сопротивления и радиусы инерции плоских фигур. Версия для печати.
(Моменты инерции сечений = статические моменты сечений J даны для главных центральных осей. Радиус инерции i=(J/F)1/2, где F — площадь сечения).
Легенда:
|
Легенда:
|
||
|
Форма поперечного сечения |
Осевой момент инерции, J, см4 |
Момент сопротивления W, см3 |
Радиус инерции i, см |
Круг.gif) |
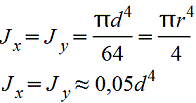 |
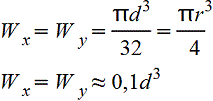 |
.gif) |
Кольцо.gif) c=d1/d |
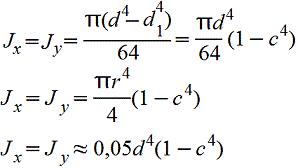 |
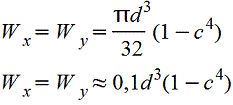 |
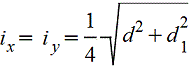 |
Тонкостенное кольцо.gif) s≤(D/10) |
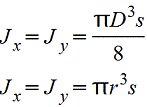 |
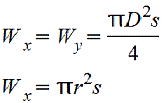 |
.gif) |
Полукруг.gif) Vo=2d/3π=0,2122d=0,4244r |
.gif) |
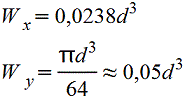 |
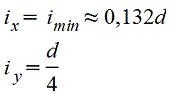 |
Круговой сегмент.gif) 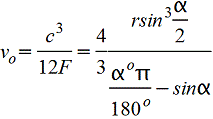 |
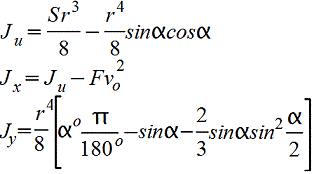 |
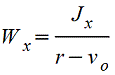 |
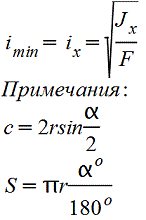 |
Круговой сектор.gif) 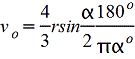 |
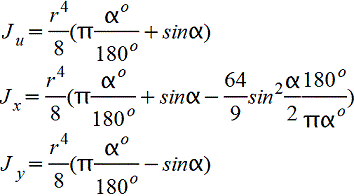 |
— | 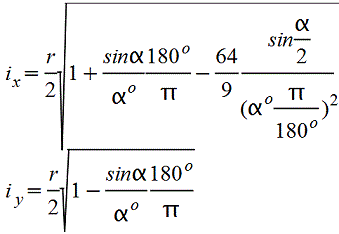 |
Круговое полукольцо.gif) .gif) |
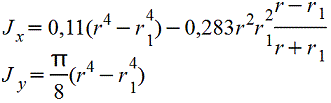 |
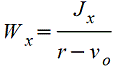 |
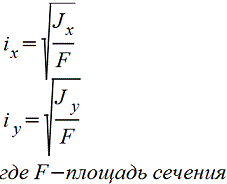 |
Сектор кругового кольца.gif) 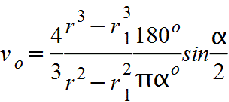 |
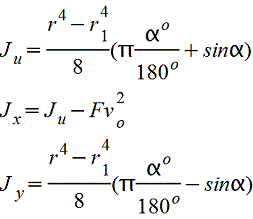 |
— | 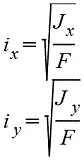 |
Профиль с симметричными закруглениями.gif) |
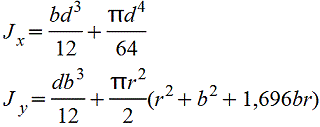 |
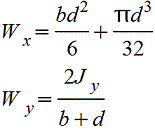 |
— |
|
Эллипс |
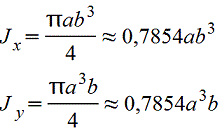 |
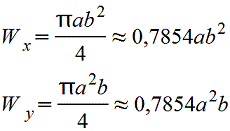 |
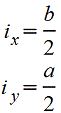 |
|
Квадрат |
 |
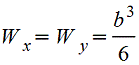 |
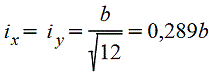 |
|
Полый квадрат |
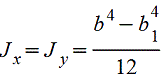 |
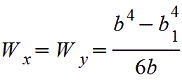 |
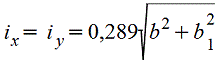 |
|
Полый тонкостенный квадрат
|
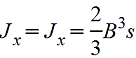 |
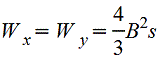 |
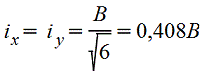 |
Квадрат, поставленный на ребро.gif) |
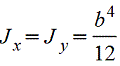 |
Срез верхнего и нижнего углов увеличивает Wx; при срезе углов на С=1/18 диагонали с каждой стороны момент сопротивления увеличивается до Wx=0,124b3 |
|
Полый квадрат, поставленный на ребро.gif) |
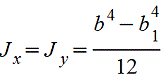 |
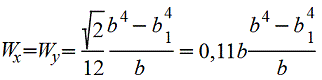 |
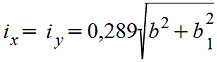 |
|
Прямоугольник |
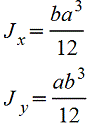 |
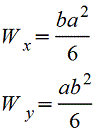 |
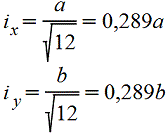 |
Прямоугольник повернутый.gif) 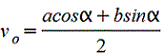 |
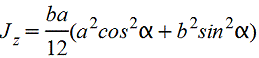 |
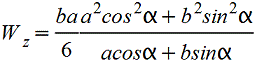 |
|
|
Полый прямоугольник |
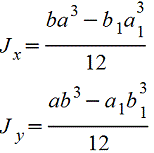 |
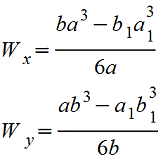 |
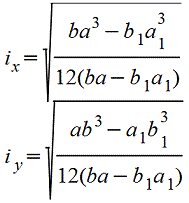 |
|
Полый тонкостенный прямоугольник |
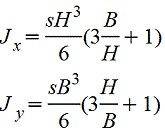 |
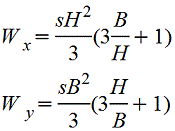 |
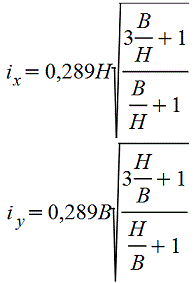 |
|
Сечение из двух равных прямоугольников |
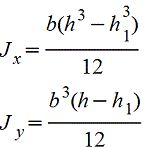 |
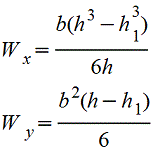 |
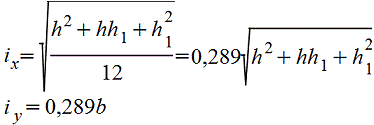 |
|
Треугольник |
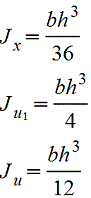 |
При вычислении напряжения в вершине треугольника |
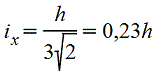 |
|
Поставленный на ребро треугольник |
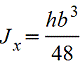 |
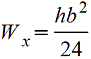 |
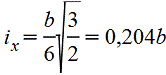 |
|
Трапеция |
.gif) |
При вычислении напряжений в точках верхнего основания |
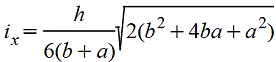 |
|
Трапеция |
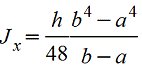 |
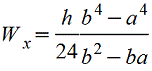 |
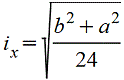 |
|
Тавр |
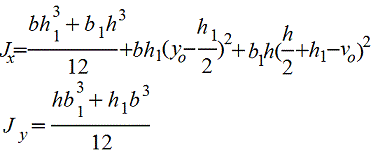 |
Для нижних волокон_25.gif) Для верхних волокон _25.gif) |
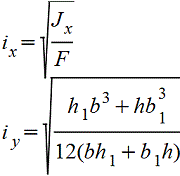 |
|
Корытное сечение |
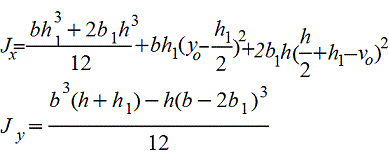 |
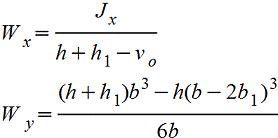 |
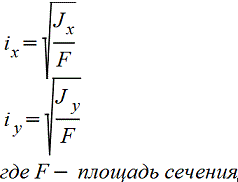 |
|
Крестообразное сечение |
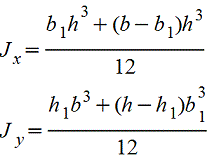 |
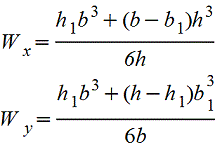 |
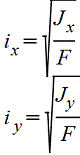 |
|
Правильный шестиугольник |
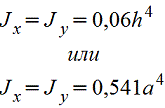 |
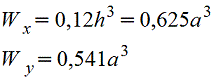 |
|
|
Правильный восьмиугольник |
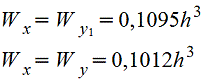 |
Момент инерции тела относительно оси. Радиус инерции.
Положение центра масс характеризует распределение масс системы не полностью. Например (рис.32), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).
Рис.32
Поэтому в механике вводится еще одна характеристика распределения масс — момент инерции. Моментом инерциитела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси
Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.
Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.
Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении.
Рекомендуемые материалы
Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси, .
Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина , определяемая равенством
,
где М — масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
В случае сплошного тела, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве , обратится в интеграл. В результате, учитывая, что
, где
— плотность, а V-объем, получим
или
Интеграл здесь распространяется на весь объем V тела, а плотность и расстояние h зависят от координат точек тела.
Моменты инерции некоторых однородных тел:
1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относительно оси Аz, перпендикулярной к стержню и проходящей через его конец А (рис. 33).
Рис.33
Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса , где
— масса единицы длины стержня. В результате
Заменяя здесь его значением, найдем окончательно:
2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.34,а).Так как все точки кольца находятся от оси Cz на расстоянии hk=R, то
Следовательно, для кольца
Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси.
3. Круглая однородная пластина или цилиндр радиуса R и массы М. Вычислим момент инерции круглой пластины относительно оси Сz, перпендикулярной к пластине и проходящей через ее центр (см. рис.34,а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.34,б).
Рис.34
Площадь этого кольца равна , а масса
, где
— масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
а для всей пластины . Заменяя здесь
его значением, найдем окончательно
Такая же формула получится, очевидно, и для момента инерции однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.34,в).
Обратите внимание на лекцию «Методы разрушения нефтяных эмульсий».
4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:
а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у — вдоль BD):
б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):
г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра):
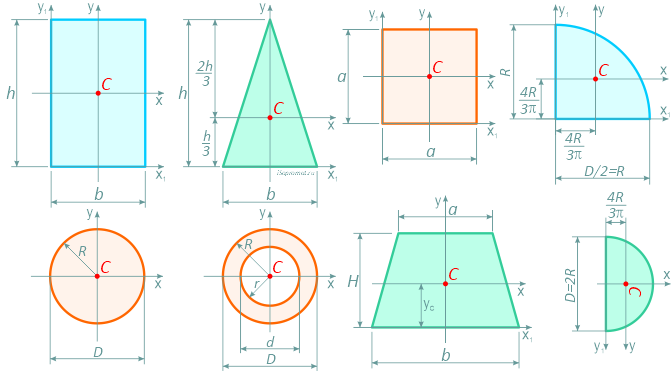
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
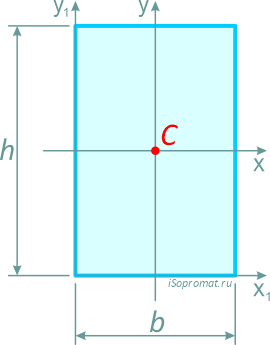
Прямоугольник
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
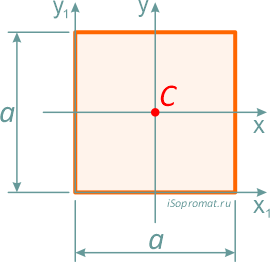
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
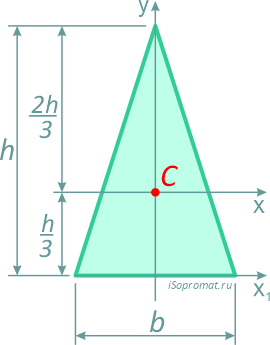
Треугольник равнобедренный
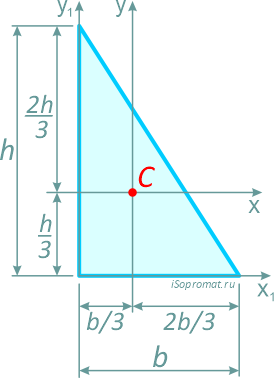
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
Прямоугольный треугольник
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
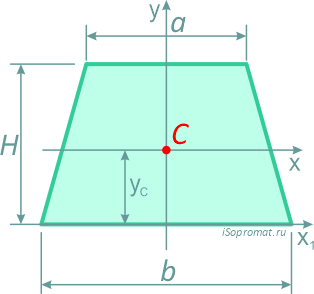
Трапеция
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
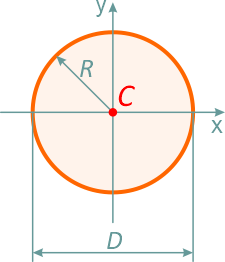
Круг
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
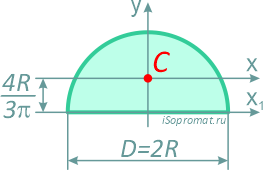
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
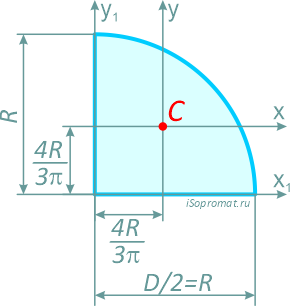
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
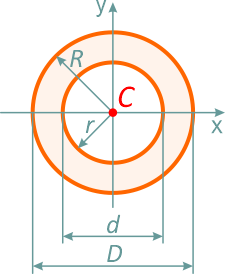
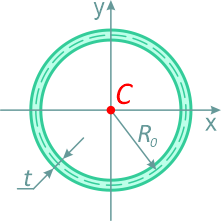
Кольцо
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее






.gif)
.gif)
.gif)
.gif)
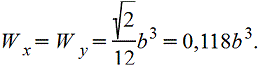
.gif)
.gif)
.gif)
.gif)
.gif)
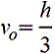
_21.gif)
_21.gif)
.gif)
.gif)

_23.gif)
_23.gif)
.gif)
.gif)
.gif)
.gif)

.gif)
.gif)
.gif)