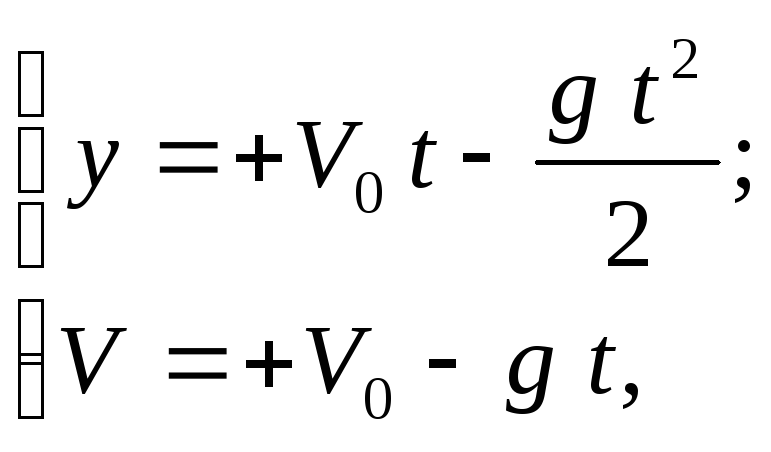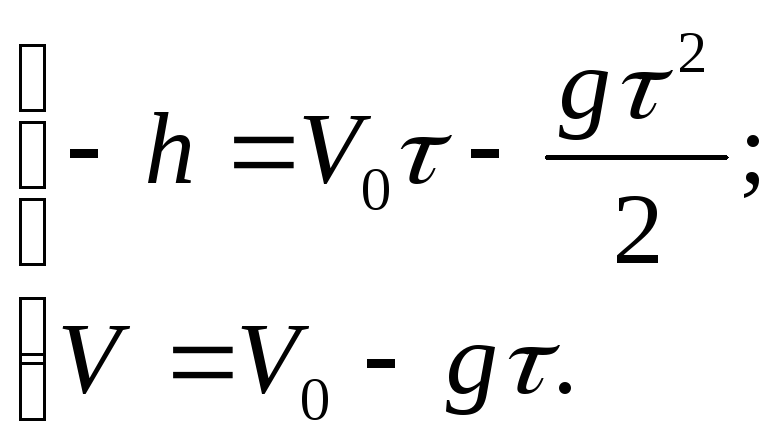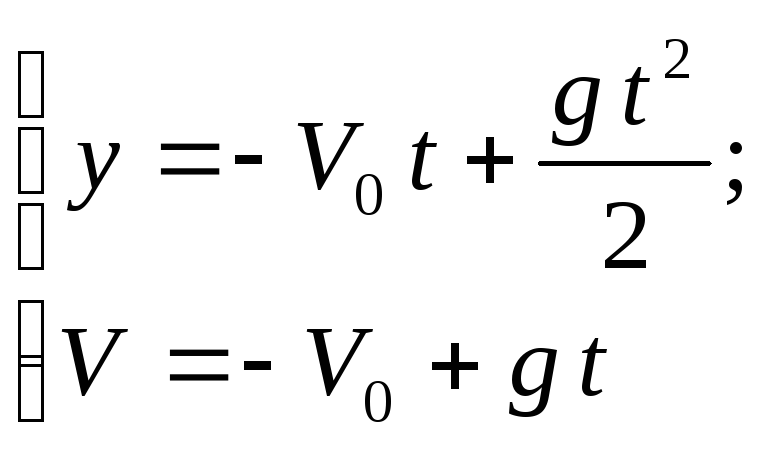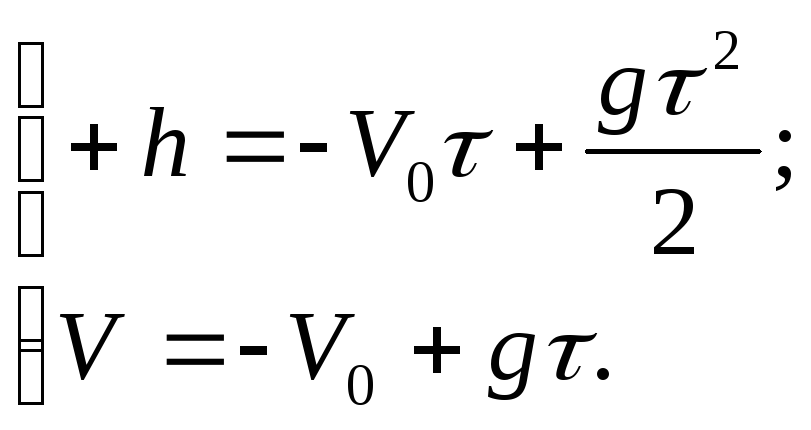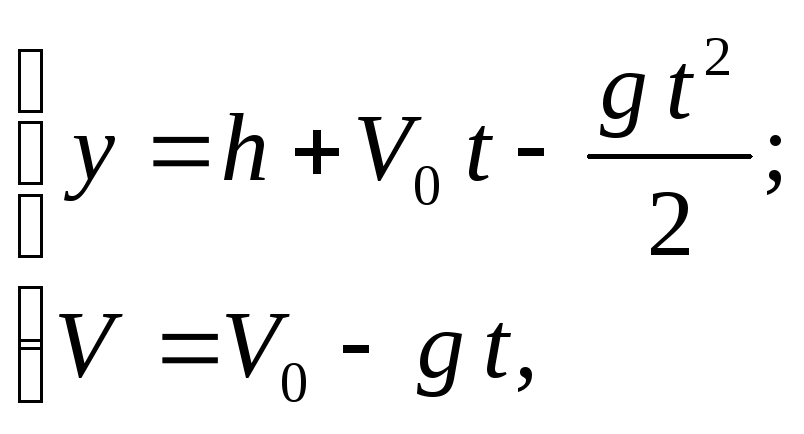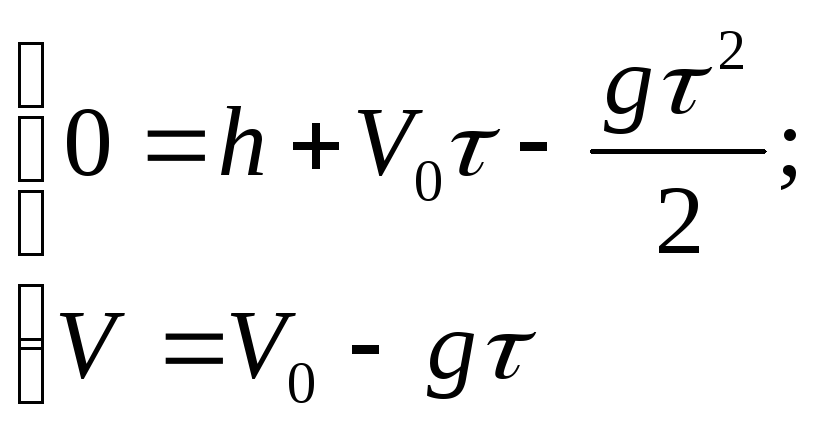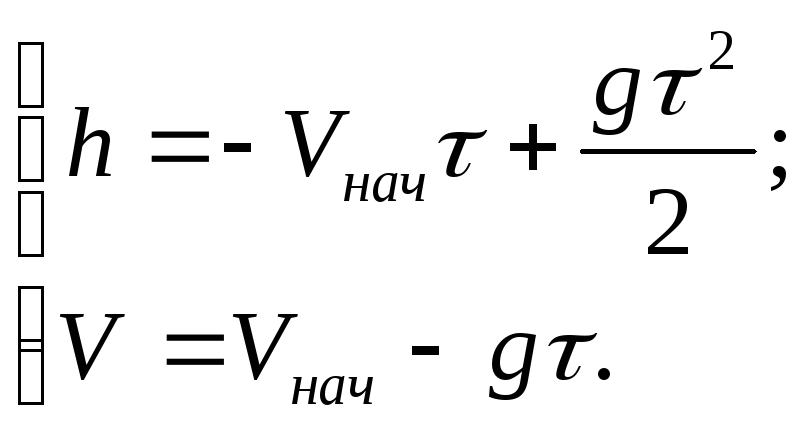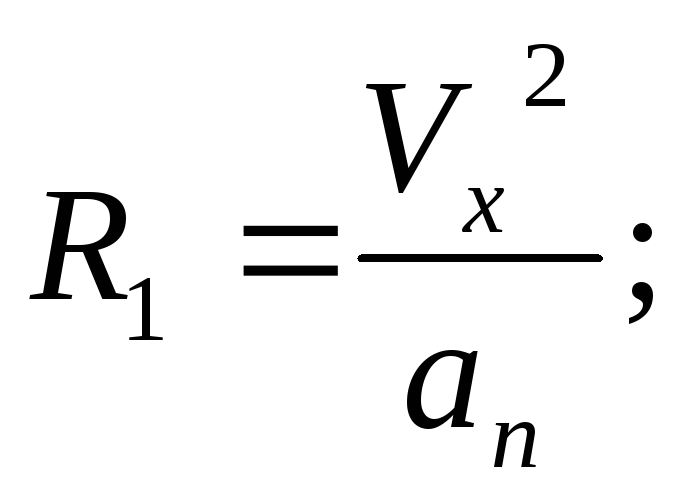Как найти радиус кривизны падения

Радиус кривизны траектории

В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из  задач представляет собой целый набор, поэтому неясностей не должно остаться.

Задача 1.

Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
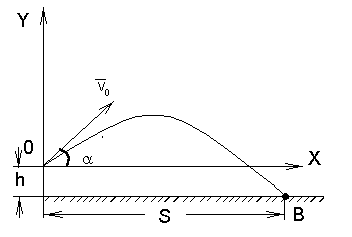
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:

Откуда :

То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.

Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому

Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:

Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:



Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :

Определим полную скорость тела в момент времени :

Угол наклона вектора скорости к горизонту в этот момент равен:

А можно было сразу и косинус найти:

Тогда искомый радиус кривизны траектории равен:

Ответ: м, м, м.

Задача 2.

Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:

По условию :





б) Мы уже определили , осталась максимальная высота подъема.

Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:



Приравниваем и :

Откуда .



Ответ: а) , б) .

2 комментария

2018-07-15   

Тело брошено горизонтально со скоростью 4 м/с с высоты 1 м. Определите радиусы кривизны траектории в ее начальной и конечной точках.

Решение:

Для определения радиуса кривизны следует воспользоваться формулой $a_{ц} = frac{v^{2} }{R}$, где $v$ — мгновенная скорость, $a_{ц}$ — центростремительное ускорение, направленное перпендикулярно скорости. $R = frac{v^{2} }{a_{ц} }$. В начальный момент скорость $v_{0}$ направлена горизонтально (рис.); $g = a_{ц}$, откуда

$R_{0} = frac{v_{0}^{2} }{g}, R_{0} = frac{4^{2} }{9,8} = 1,63 м$.

В конечный момент времени мгновенная скорость $v$ направлена под углом $alpha$ к ускорению свободного падения $vec{g}$. $v_{x} = v_{0}, v_{y} = — gt$, где $t = sqrt{ frac{2h}{g} }$. Следовательно,

$v_{к} = sqrt{v_{x}^{2} + v_{y}^{2} } = sqrt{ v_{0}^{2} + 2gh }$.

Чтобы найти радиус кривизны в конечной точке, определим центростремительное ускорение в этой точке, для чего найдем проекцию ускорения свободного падения $vec{g}$ на перпендикуляр к направлению скорости $vec{v}_{к}: a_{ц.к} = g sin alpha$, где

$sin alpha = frac{v_{x} }{v_{кон} } = frac{v_{0} }{ sqrt{v_{0}^{2} + 2gh } }, R_{к} = frac{v_{к}^{2} }{a_{ц.к} } = frac{ ( sqrt{v_{0}^{2} + 2gh } )^{3} }{gv_{0} }$

$R_{к} = frac{( sqrt{ 4^{2} + 2 cdot 9,8 cdot 1 } )^{3} }{9,8 cdot 4} = 5,4 м$.

Как найти радиус кривизны траектории

При рассмотрении движения тел используется ряд характеризующих величин, например тангенциальное и нормальное (центростремительное) ускорение, скорость, а также кривизна траектории. Радиус кривизны – геометрическое понятие, обозначающее радиус окружности R, по которой движется тело. Этот параметр можно найти по соответствующим формулам с помощью заданной траектории движения.

Инструкция

Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Его вычисление будет основываться на применении формулы аn = V²/R. Здесь радиус R выявляется из отношения нормального ускорения аn и мгновенной скорости V движения тела. Узнав данные величины, можно легко найти искомую компоненту R.

Вычислите проекции скорости тела на осях (ОХ, ОY). Математический смысл скорости – это первая производная от уравнения движения. Поэтому они легко находятся взятием производной от заданных уравнений: Vx = x’, Vy = y’. При рассмотрении геометрического отображения данных проекций в координатной системе видно, что они являются катетами прямоугольного треугольника. Причем гипотенуза в нем – искомая мгновенная скорость. Исходя из этого, вычислите величину мгновенной скорости V по теореме Пифагора: V = √( Vx² + Vy²). Подставляя в выражение известное значение времени, найдите числовой показатель V.

Модуль нормального ускорения также легко определить, рассмотрев другой прямоугольный треугольник, образуемый модулем полного ускорения а и касательного ускорения тела ак. Причем здесь нормальное ускорение является катетом и вычисляется так: аn = √( а² — ак²). Для нахождения касательного ускорения продифференцируйте по времени уравнение мгновенной скорости движения: ак = |dV/dt|. Полное же ускорение вычислите по его проекциям на оси, аналогично нахождению мгновенной скорости. Только для этого возьмите от заданных уравнений движения производные второго порядка: ах = х», аy = y». Модуль ускорения а = √( ах2 + аy2). Подставляя все найденные величины, определите числовое значение нормального ускорения аn = √( а² — ак²).

Выразите из формулы аn = V²/R искомую переменную радиуса кривизны траектории: R = V²/ аn. Подставьте числовые значения скорости и ускорения, вычислите радиус.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Решение

В
течение всего времени, пока камень
движется, его движение совершается по
одному и тому же закону. Действительно,
ускорение камня равное ускорению
свободного падения, если пренебречь
сопротивлением воздуха, все время
остается неизменным, следовательно,
движение камня является равнопеременным
движением с отличной от нуля начальной
скоростью. Закон движения не меняется
в тот момент, когда скорость изменяет
свое направление на противоположное
первоначальному.

Движение камня проходит по закону

(1)

его скорость

(2)

Знаки
начальной скорости и ускорения и
численное значение определяются выбором
положительного направления оси и начала
отсчета.

Рассмотрим
эту задачу в трех случаях.

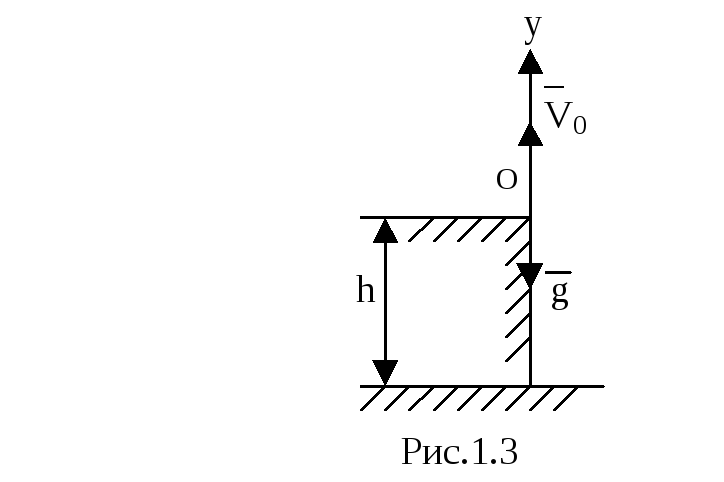
1) Ось OY
направлена
вверх, начало отсчета помещается на
уровне земли (рис.1.3) Тогда при
.

Уравнения (1) и (2)
примут вид

при t
= τ,
y
= —h

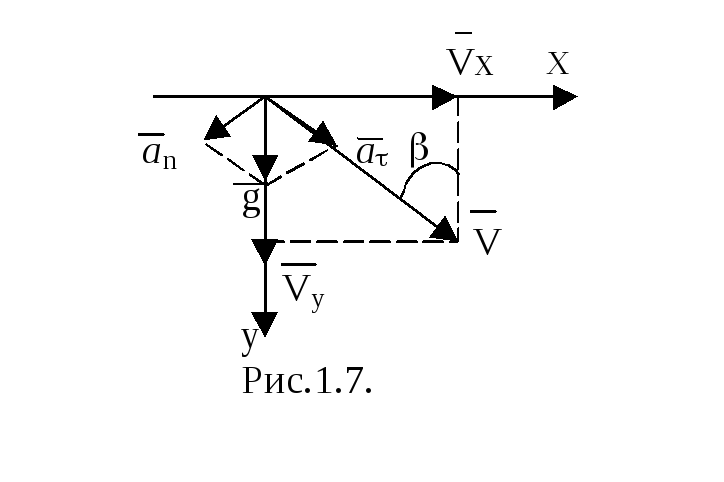
2) Ось OY
направлена вниз, начало отсчета на
уровне земли (рис 1.4). Тогда при
.

Уравнение
имеют вид

при t
= τ
y
= + h

3) Ось OY
направлена вверх, начало отсчета на
уровне дна колодца (рис.1.5). Тогда при

У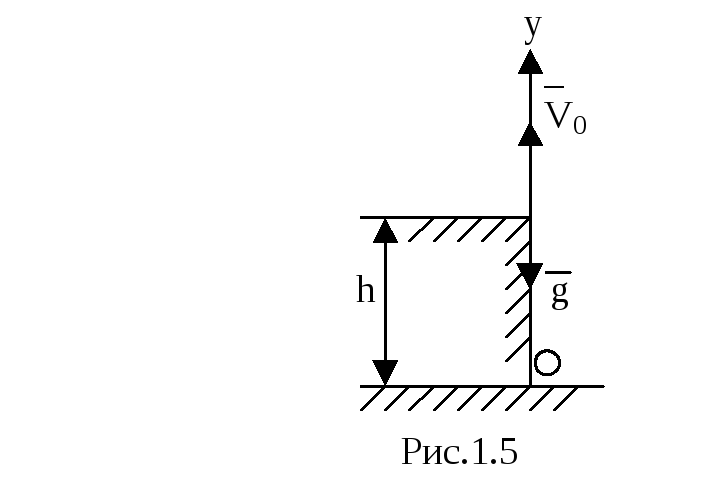равнение
движения имеет вид

при t
= τ,
y
= 0, тогда

Все три варианта
дают одинаковые уравнения движения при
t
= τ

Для определения

решим
квадратное уравнение

Корень
его не учитываем, так как он не имеет
физического смысла.

а) Можно найти
максимальную высоту подъема камня,
исходя из того, что дискриминант

Тогда
а максимальное значение

м;

б)
Найти время, по истечении которого
камень находится в любой промежуточной
точке своего пути.

При
,имеет два значения, так как в каждой
точке камень бывает дважды за время
движения.

Задача 5.
Камень брошен с высоты h=2,1
м под углом 
= 45˚ к горизонту и падает на землю на
расстоянии S
= 42 м (по
горизонтали) от места бросания. Найти
начальную скорость V₀
камня,
время полета τ и максимальную высоту
подъема над уровнем земли. Определить
также радиусы кривизны траектории в
верхней точке и в точке падения камня
на землю.

Дано:Решение

h
= 2,1 м

 = 45˚

S
= 42 м

V₀
— ? τ
— ? H
— ?

R₁
и R₂
— ?

Рис.1.6

Движение камня,
происходящее по параболе, можно
рассматривать как сумму двух независимых
движений: равномерного движения по
горизонтали (по оси Х)
и равнопеременного по вертикали (по оси
Y).
Начало отсчета удобно выбрать в точке
бросания. Ось Y
направлена вертикально вверх.

Для движения камня
по оси Х
получаем

;при
t
= τ x
= S
.

Следовательно,

(1)

Для движения по
оси OY

(2)

.
(3)

При t
= τ,
y
= 
h,
поэтому

(4)

(5)

Решая совместно
уравнения (1) и (4), находим τ и V₀:

1) τ
=

с,

2)

3) Высоту подъёма
камня можно найти из условия H
= h
+ y_max
.

При

отсюда
(
– время подъёма камня).

Подставив

в уравнение (4), получим
тогда

м.

4) Для определения
радиуса кривизны траектории в данной
точке нужно определить по величине и
направлению вектор полного ускорения.
В верхней точке траектории
,следовательно,
векторы ускорения и скорости взаимно
перпендикулярны. Это значит, чтоa_τ
= 0,
a_n
= g.
Зная ускорение
и скорость, найдём радиус кривизны
траектории в верхней точке.

;

и

В
конечной точке траектории синус угла
βмежду векторами
скорости и ускорения может быть выражен
как показано на рис.1.7.

Разложим вектор
полного ускорения на нормальное и
тангенциальное, получим

Радиус траектории
в этой точке находится из соотношения

т.е.

Тогда R₂
= 63 м.

Ответ:

З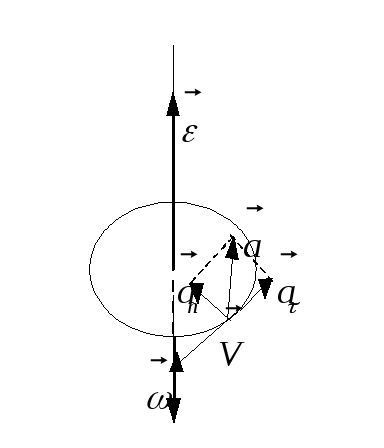адача
6. Тело
вращается вокруг неподвижной оси по
закону φ
= 10 + 20 t
– 2 t²
рад. Найти: 1) Угловую скорость, угловое
ускорение и полное ускорение точки,
находящейся на расстоянии R
= 0,1 м от оси вращения, для момента времени

= 4 с (рис.
1.8). 2) Через сколько времени тело
остановится? 3)Сколько оборотов сделает
до остановки?

Дано:

φ
= 10
+ 20 t
–2 t²
рад

R
= 0,1 м

= 4 c

 = 0

— ?
ε
— ?
a
—?
t
— ?
N
— ?

Рис.
1.8

Соседние файлы в папке Часть 1

• #
• #
• #
• #
• #
• #

С башни брошено тело в горизонтальном направлении со скоростью 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через 2 с после начала движения.

Эта задача была размещена посетителями в разделе Решаем вместе 9 октября 2007 года.

Решение:

Радиус кривизны траектории — это радиус окружности R, по которой в этот момент движется тело.

Через две секунды тело приобретет скорость v, в которой вертикальная составляющая равна v_y = gt:

v = √(vx2 + vy2) = √(vx2 + (gt)2).

(1)

Нормальное ускорение тела a_n:

откуда радиус окружности R равен:

Нормальное ускорение a_n связано соотношением:

где

тогда:

Подставляя (3) и (1) в (2), получим:

R =	vv2	=	√(vx2 + (gt)2)	• (vx2 + (gt)2).
gvx	gvx

После вычислений R = 104,2 м.

[тема: задачи на криволинейное движение]

---