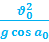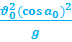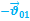Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
Тело брошено со скоростью 10 м/с под углом 
к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
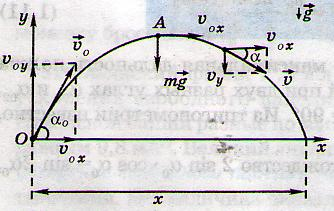
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м, м, м.
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и :
Откуда .
Ответ: а) , б) .
Как найти радиус кривизны траектории
При рассмотрении движения тел используется ряд характеризующих величин, например тангенциальное и нормальное (центростремительное) ускорение, скорость, а также кривизна траектории. Радиус кривизны – геометрическое понятие, обозначающее радиус окружности R, по которой движется тело. Этот параметр можно найти по соответствующим формулам с помощью заданной траектории движения.
Инструкция
Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Его вычисление будет основываться на применении формулы аn = V²/R. Здесь радиус R выявляется из отношения нормального ускорения аn и мгновенной скорости V движения тела. Узнав данные величины, можно легко найти искомую компоненту R.
Вычислите проекции скорости тела на осях (ОХ, ОY). Математический смысл скорости – это первая производная от уравнения движения. Поэтому они легко находятся взятием производной от заданных уравнений: Vx = x’, Vy = y’. При рассмотрении геометрического отображения данных проекций в координатной системе видно, что они являются катетами прямоугольного треугольника. Причем гипотенуза в нем – искомая мгновенная скорость. Исходя из этого, вычислите величину мгновенной скорости V по теореме Пифагора: V = √( Vx² + Vy²). Подставляя в выражение известное значение времени, найдите числовой показатель V.
Модуль нормального ускорения также легко определить, рассмотрев другой прямоугольный треугольник, образуемый модулем полного ускорения а и касательного ускорения тела ак. Причем здесь нормальное ускорение является катетом и вычисляется так: аn = √( а² — ак²). Для нахождения касательного ускорения продифференцируйте по времени уравнение мгновенной скорости движения: ак = |dV/dt|. Полное же ускорение вычислите по его проекциям на оси, аналогично нахождению мгновенной скорости. Только для этого возьмите от заданных уравнений движения производные второго порядка: ах = х», аy = y». Модуль ускорения а = √( ах2 + аy2). Подставляя все найденные величины, определите числовое значение нормального ускорения аn = √( а² — ак²).
Выразите из формулы аn = V²/R искомую переменную радиуса кривизны траектории: R = V²/ аn. Подставьте числовые значения скорости и ускорения, вычислите радиус.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
201). Окружность с центром в точке Р и радиусом, равным радиусу кривизны кривой в данной точке , называется кругом кривизны. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. 7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.
Чем больше радиус окружности, тем меньше ее кривизна. Так как кривизна кривой, вообще говоря, изменяется при переходе от данной ее точки к другой, то и радиус кривизны является переменной величиной. Длина, на которую сматывается нить с эволюты, равна, очевидно, приращению радиуса кривизны эвольвенты. Обычно кривизна определяется для каждой точки на «объекте» и выражается как значение некоторого дифференциального выражения 2-го порядка.
В этой статье приводятся только несколько простейших примеров определений понятия кривизны. Если кривизна кривой равна нулю, то соприкасающаяся окружность вырождается в прямую. Главные кривизны являются экстремальными значениями нормальных кривизн.
Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме: где (t) − параметр. Нахождение радиуса кривизны траектории – одна из важных тем школьного курса физики, т.к. решение ряда задач динамики связано с нахождением радиуса кривизны траектории.
Существует несколько способов нахождения радиуса кривизны, один из которых связан с использованием дифференциального исчисления, а другой основан на применении физических понятий. При рассмотрении движения тел используется ряд характеризующих величин, например тангенциальное и нормальное (центростремительное) ускорение, скорость, а также кривизна траектории.
Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Обычно кривизну определяют в отдельности для каждой искомой точки на заданном «объекте» и обозначают ее как значение второго порядка дифференциального выражения.
Определить, линзы какого радиуса кривизны вам нужны, может врач офтальмолог, произведя необходимые замеры. В медицинском центре или клинике врач офтальмолог после проведения специальных замеров (например, при помощи авторефкератометра), определит базовую кривизну Ваших глаз и выпишет Вам рецепт.
I. Окружность имеет одинаковую кривизну во всех своих точках. Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.
Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное an = v2/R, где R – радиус кривизны траектории. Если же постоянным остается только числовое значение касательного уравнения at = dv/dt = f'(t) = const, то an≠0 и такое движение точки называется равнопеременным криволинейным.
Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные. При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну) траектории. Здесь – орты осей и ; – проекции скорости и ускорения точки на оси координат.
Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу an = v2/R, выражающую числовое значение нормального ускорения. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом.
Читайте также:
1) найти радиус кривизны траектории в наивысшей точке полета. 
.
2)найти радийс кривизны траектории в начальной точке полета.
.
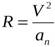
3) найти радиус траектории.
Центр масс твёрдого тела движется так же как двигалась бы материальная точка, масса которой равна массе тела, под действием внешних сил, приложенных к данному телу.
Тело состоит из нескольких элементов. Уравнение i-го элемента массой m записывается так:
Где Fi внешняя сила, а ∑Fik это сумма внутренних сил, действующих на i-ый элемент со стороны всех других элементов.
Сложим все аналогичные уравнения для всех элементов. Т.к. Fik = -Fki третьему закону Ньютона, то их сумма равна нулю.
После сложения получим:
Устойчивое равновесие — это равновесие, при котором, тело, выведенное из положения равновесия, вернётся в то же положение.
Неустойчивое равновесие — если тело, после смещения, не вернётся в это положение.
Скорость точки, движущейся по окружности ,часто называют Линейной скоростью ,чтобы подчеркнуть ее отличие от угловой скорости. Между линейной скоростью точки, обращающейся по окружности, и ее угловой скоростью существует связь. При равномерном движении точки по любой траектории модуль скорости равен s/∆t
Точка A, движущаяся по окружности радиуса R,за время ∆t проходит путь равный дуге A1A2
S=A1A2=∆ϕR .Модуль линейной скорости движения v= s/∆t ==∆ϕR/∆t=ωR
Итак , модуль линейной скорости точки, движущейся по окружности, равен произведению угловой скорости на радиус окружности :
Эта формула справедлива как для равномерного, так и для неравномерного движения точки по окружности.
Модуль ускорения точки, движущейся по окружности, можно выразить через угловую скорость тела и радиус окружности. Так как a=v²/R и v= ωR
Центростремительное ускорение.
Центростремительное ускорение (нормальное ускорение) — ускорение, направленное перпендикулярно мгновенной скорости и изменяющее ее по направление.
За время t точка А совершиит перемещение АА1 = r . Рассмотрю треугольники ОАА1 и А1СВ (см. рисунок 1.82, а).Углы при вершинах этих равнобедренных треугольников равны( так как 
соответствующие стороны перпендикулярны ). => треугольники подобны. =>
Разделим обе части равенства на t, перейдем к пределу при стремлении интервала времени t 0:
Предел в левой части равенства есть модуль мгновенного ускорения, а предел в правой части равенства представляет собой модуль мгновенной скорости точки. Поэтому равенство примет вид:
Отсюда:
Очевидно, что модуль ускорения при равномерном движении точки по окружности есть постоянная величина, так как U и r не изменяются при движении
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9614 — 
| 7509 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
1.59. Радиус кривизны траектории в точке бросания: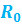 
= 
1.60. Радиус кривизны траектории в точке максимальной высоты А :
= 
Замечание1: радиус кривизны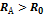 
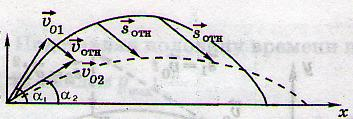
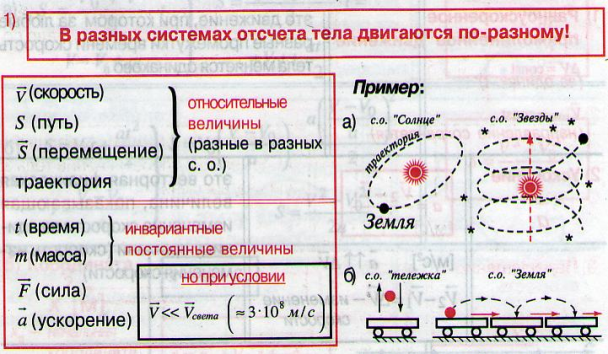
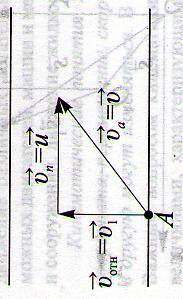
…- сравнить …
Как будут двигаться относительно друг друга два тела брошенные одновременно под разными углами к горизонту?
1.61.
… —второе тело относительно первого тела будет двигаться равномерно и прямолинейно, и вектор перемещения, соединяющий тела, в любой момент времени будет параллелен вектору относительной скорости:
= 
= 
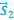
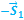
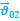
Относительность механического движения
§ 1.6.
1.63. Относительность скорости. 
= 
—скрость пловца относительно воды(относительная скорость);
= 
—скорость течения отностительно берега (переносная скорость).
= 
—скорость пловца относительно берега (абсолютная скорость)
= 
+ 
(1)
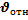
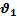
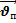
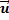
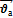
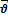
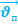
…- формула сложения скоростей
= 
+ 
(2)
…- формула сложения перемещений.
Замечание: формулы (1) и (2) формулы преобразования Галилея.
Пойдем в обратном порядке.
gh=3/4*(2/3*(g*t)^2);
t=(3*h/*g)^0,5, где g – ускорение свободно падения;
t
0,3 c
А Митин Андрей, по-моему, проврался: в выражении t=2/(h*(8*g*h/5)^0.5) проблемы с размерностью.
2) Аппроксимируем движение точки равномерным движением по окружности.
v=w*R; a=w^2*R; m=p/v=p/(w*R);
F=m*a=(p*w^2*R)/(w*R)=p*w;
F=0,1*0,5*pi Н=0,05*pi Н, где pi – число пи.
1) Тут пока выкладки получаются громоздкие – утомительно писать в подобном окне. Может, потом чего-нибудь попроще придумаю. Но ответ такой: максимальны радиус в крайних точках траектории (начальной и конечной моменты движения), а минимальный – в точке, что делит траекторию пополам и в которой движение горизонтально.
Конечные соотношения:
R(t)=v(t)^3/(g*v(0)*cos(A)), где g – ускорение свободного падения.