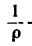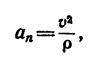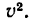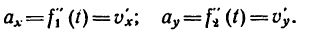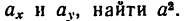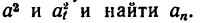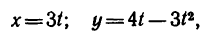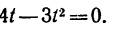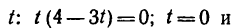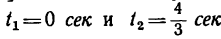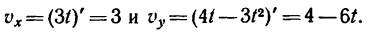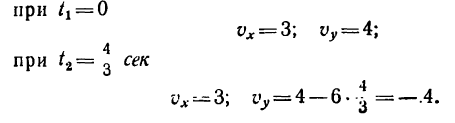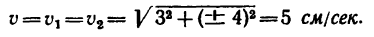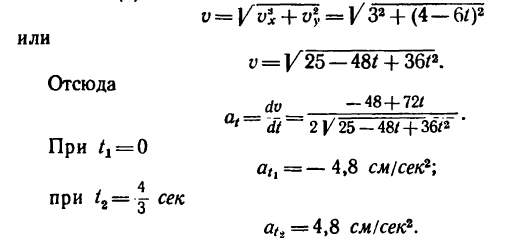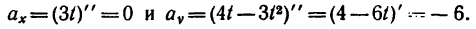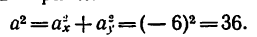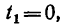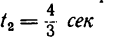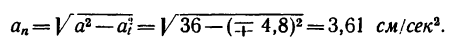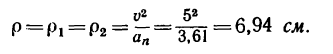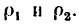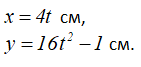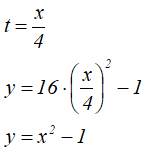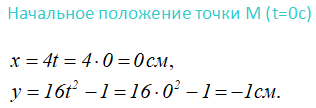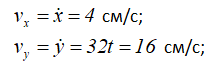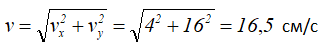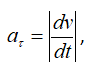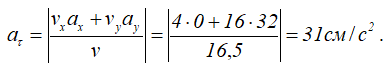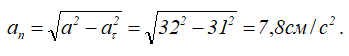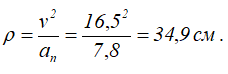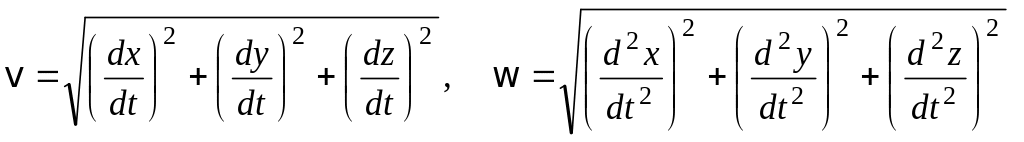Преподаватель который помогает студентам и школьникам в учёбе.
Кинематический способ определения радиуса кривизны траектории в теоретической механике
Кинематический способ определения радиуса кривизны траектории:
При решении многих технических задач возникает необходимость знать радиус кривизны р (или
Таким образом, если закон движения точки задан уравнениями
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
2. Подставив в (б’) выражения 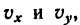
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение 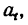
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
5. Подставив в (г) выражения
6. Подставить в (в) значения
7. Подставив в (а) найденные значения 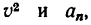
Задача:
Движение точки задано уравнениями
(х, у—в см, t — в сек). Определить радиус кривизны траектории в те моменты, когда она пересекает ось Ох.
Решение.
1. В те моменты, когда траектория пересекает ось Ох, ордината у—0. Поэтому, подставив во второе уравнение движения значение у = 0, получим
Отсюда [решая уравнение относительно 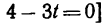
2. Находим выражения проекций скорости:
Как видно, проекция скорости на ось Ох — постоянная величина (не зависит от времени).
3. Определяем значение этих проекций в моменты пересечения траекторией оси Ох:
4. Числовое значение скорости точки в моменты пересечения траекторией оси Ох в данном случае одинаковы
5. Находим касательное ускорение точки. Для этого получим общее выражение (уравнение) скорости, воспользовавшись зависимостью (б):
6. Находим проекции полного ускорения точки:
Следовательно, в данном случае полное ускорение точки — постоянная величина. Причем
7. Определяем нормальное ускорение точки. Как при
так и при
8. Зная, что в моменты пересечения траекторией оси 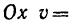
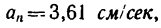
Решение этой задачи рекомендуется самостоятельно иллюстрировать чертежом, изобразив на нем траекторию точки, векторы скорости 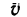
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и
. Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м,
м,
м.
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б)
.
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и
:
Откуда .
Ответ: а) , б)
.
Решение задачи (РГР) К1 «Определение скорости и ускорения точки по заданным уравнениям ее движения» по разделу «кинематика» теоретической механики.
Пример определения для заданного момента времени положения точки на траектории, скорости, полного, касательного и нормального ускорения, радиуса кривизны траектории и вида траектории движения точки, если движение точки задано уравнениями.
Задача
Движение точки M задано уравнениями:
Требуется:
Установить вид траектории движения точки M, и для момента времени t = t1 = 0,5 с найти:
- положение точки на траектории,
- скорость, полное, касательное и нормальное ускорения,
- радиус кривизны траектории.
Другие примеры решений >
Помощь с решением задач >
Решение
Расчет траектории движения точки
Уравнения движения можно рассматривать как параметрические уравнения траектории точки.
Другие видео
Чтобы узнать вид траектории в координатной форме, надо получить прямую зависимость между переменными x и y, для этого избавимся от параметра времени t, выразив его, например, из первого уравнения и подставив во второе.
Получилось квадратное уравнение. То есть точка движется по параболе.
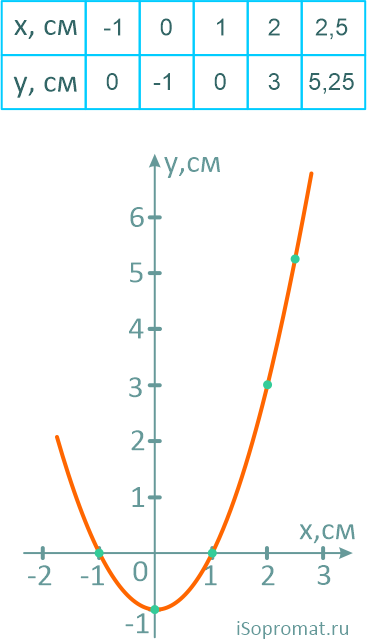
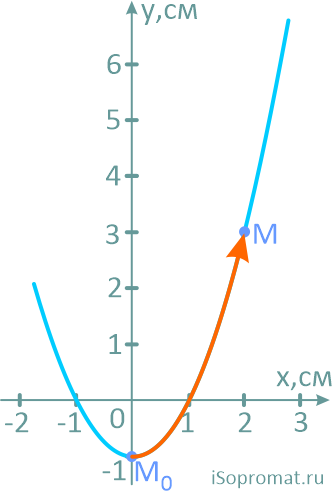
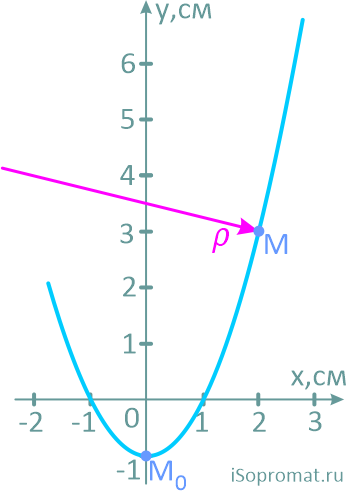
Построим траекторию движения, рассчитав несколько её точек.
Положение точки на траектории
Определим положения точки в начале движения и в заданный момент времени.
Для этого в исходные уравнения подставляем соответственно сначала 0
а затем, половину секунды.
Положение точки на ее траектории в заданный момент обозначим буквой M, и все остальные параметры будем рассчитывать для неё.
Расчет скорости точки
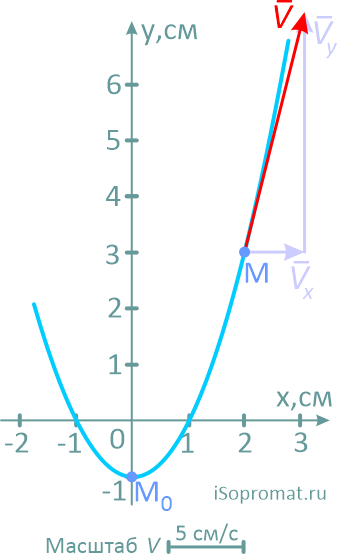
Направление и величину скорости точки определим как векторную сумму её проекций на оси координат.
Здесь i, j — орты осей x и y.
vx, vy — проекции вектора скорости на оси координат.
Проекции вектора скорости получим, взяв первые производные по времени t от соответствующих заданных уравнений движения точки.
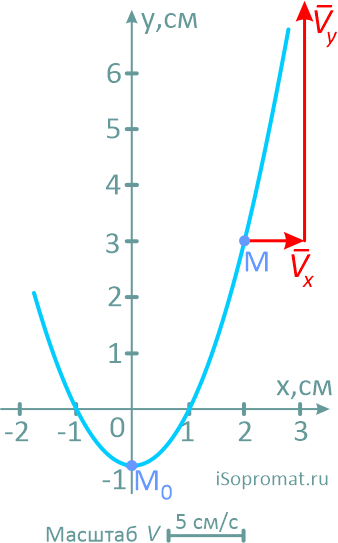
Далее выбрав масштаб, из точки M последовательно и с учетом знака, откладываем оба вектора.
Сам вектор скорости получим, соединив точку M с концом второго вектора и направив его по ходу движения точки.
Здесь надо отметить, что вектор скорости всегда должен располагаться по касательной к траектории. Любое другое положение будет указывать на ошибки в расчетах.
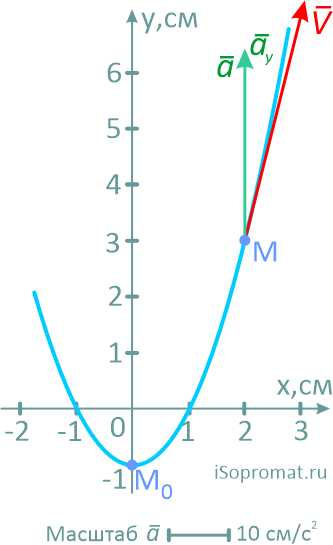
Рассчитаем модуль вектора скорости
Расчет ускорений точки
Проекции полного ускорения точки на оси координат определяются как вторая производная от исходных уравнений движения точки.
Здесь, ax, ay – проекции ускорения точки на оси координат.
В этом примере, горизонтальная проекция ускорения оказалась равной нулю, поэтому его модуль и направление будут совпадать с вертикальной.
Касательная составляющая полного ускорения это производная скорости точки по времени.
Ее можно рассчитать по этой формуле.
Вектор касательного ускорения всегда направлен по линии вектора скорости.
Положительная величина говорит об ускоренном движении точки и тогда направления скорости и касательного ускорения совпадают.
В противном случае они разнонаправлены, и движение точки замедляется.
Модуль нормального ускорения определим по формуле Пифагора, так как векторы касательного и центростремительного ускорений всегда взаимно перпендикулярны.
Расчет радиуса кривизны траектории
Осталось найти только радиус кривизны траектории в точке M, который равен отношению квадрата скорости к модулю нормального ускорения.
Результаты расчетов
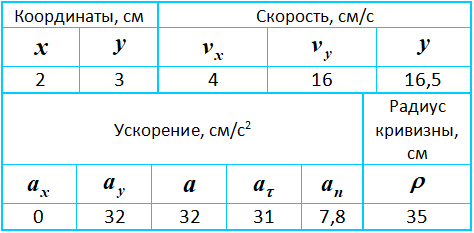
Результаты вычислений для заданного момента времени t1=0,5c приведены в таблице:
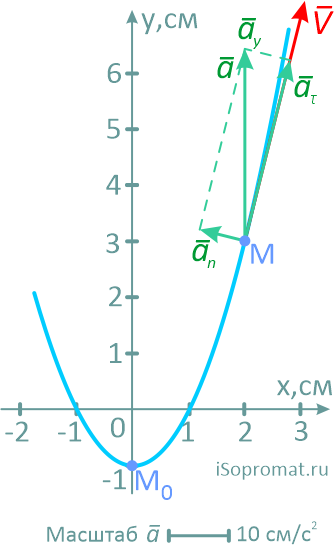
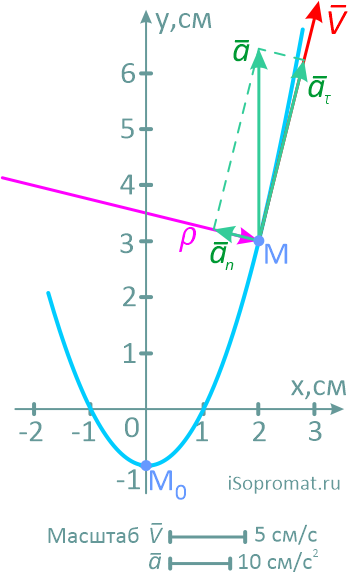
На рисунке показано положение точки M в заданный момент времени и векторы скорости и ускорений в выбранном масштабе.
Вектор v строим по составляющим vx и vy, причем этот вектор должен по направлению совпадать с касательной к траектории.
Вектор a строим по составляющим ax и ay и затем раскладываем на составляющие векторы aτ и an. Совпадение величин aτ и an, найденных из чертежа, с их значениями, полученными аналитически, служит критерием правильности решения.
Другие примеры решения задач >
Определение радиуса кривизны траектории точки
В том случае, когда
движение задано координатным способом,
радиус кривизны траектории определяется
следующим образом:
по формулам
координатного способа задания движения
(1.1) определяются скорость и полное
ускорение точки:
;
по формулам
траекторного способа задания движения
(1.2) определяются нормальное и касательное
ускорения:
,
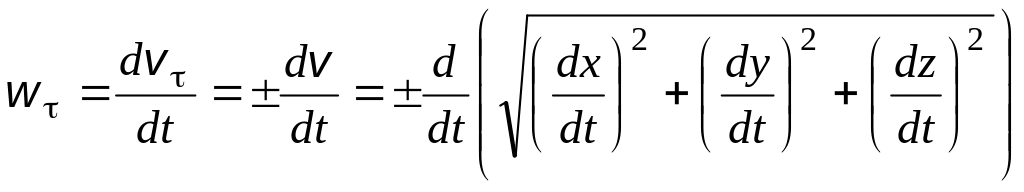
и далее
радиус кривизны траектории по формуле
(1.3):
. (1.4)
Порядок выполнения задания
Движение точки
задано кинематическими уравнениями в
соответствии с номером варианта задачи
(см. таблицу «Исходные данные» с. 10-14).
1. Определить
траекторию точки и изобразить ее на
чертеже. Указать на ней положение точки
в заданные моменты времени, обозначив
их М0
и М1
(М0
– в момент
времени t = 0;
М1
в момент t = t1).
2. Определить
алгебраические величины проекций
скорости точки в общем виде, а затем для
момента времена
t = t1.
По найденным алгебраическим величинам
проекций скорости построить вектор на
чертеже и вычислить его величину.
3. Определить
алгебраические величины
проекций ускорений точки на оси координат
в общем
виде, а затем для
момента времени
t = t1.
Построить вектор ускорения на чертеже
и вычислить его величину.
4. Для
определения касательного ускорения
необходимо иметь проекцию вектора
скорости точки на касательную в виде
функции времени:
,
тогда касательное ускорение точки
опреде-ляется по формуле
.
Определить
для момента време-ни
t = t1
и построить этот вектор на чертеже.
5. Установить
характер движения точки в момент времени
t = t1
(по направлениям векторов
и
).
Если векторы сонаправлены, то движение
точки ускоренное, если они противоположны
по направлению, то – замедленное.
6. Нормальное
ускорение точки в момент времени
определяется из равенства
,
в котором
каждый из векторов
и
вычислен в этот момент времени. Вектор
построить на чертеже.
7. Радиус
кривизны траектории точки в момент
времени t = t1
определить по формуле (1.4).
Исходные данные
|
№ вар. |
x |
y |
z |
t1, |
|
м |
||||
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
0 |
1 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
№ вар. |
x |
y |
z |
t1, |
|
м |
||||
|
3 |
|
|
0 |
0 |
|
|
|
0 |
|
|
|
0 |
|
|
||
|
4 |
0 |
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
5 |
|
|
2 |
1 |
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
3 |
|
|
|
0 |
|
|
|
|
|
|
6 |
1 |
|
|
7 |
|
|
0 |
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
|
№ вар. |
x |
y |
z |
t1, |
|
м |
||||
|
8 |
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
0 |
|
|
|
|
9 |
|
|
0 |
|
|
0 |
|
|
||
|
0 |
|
|
|
|
|
10 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
11 |
0 |
|
|
|
|
|
0 |
|
||
|
|
|
0 |
|
|
|
12 |
|
0 |
1 |
|
|
|
|
0 |
1 |
|
|
|
0 |
|
|
|
№ вар. |
x |
y |
z |
t1, |
|
м |
||||
|
13 |
|
|
0 |
|
|
0 |
|
|
1 |
|
|
|
0 |
|||
|
14 |
|
0 |
|
|
|
0 |
||||
|
|
|
0 |
|
|
|
15 |
|
|
0 |
1 |
|
0 |
|
2 |
||
|
0 |
|
|
|
|
|
16 |
0 |
|
||
|
|
0 |
|
||
|
|
|
0 |
||
|
17 |
|
|
0 |
20 |
|
0 |
|
|
||
|
t |
0 |
|
1 |
|
|
18 |
|
|
0 |
|
|
|
0 |
|
||
|
0 |
|
|
1 |
|
№ вар. |
x |
y |
z |
t1, |
|
м |
||||
|
19 |
0 |
|
|
|
|
|
0 |
|||
|
|
0 |
|
|
|
|
20 |
|
|
0 |
|
|
|
0 |
|
1 |
|
|
0 |
|
|
1 |
П р и м е р. Движение
точки задано кинематическими урав-нениями:
;
;
;
,
где x
и y
в м,
а t
в с.
1. Определить
траекторию точки и построить её на
чертеже. Указать на ней положения точки
в заданные моменты времени, обозначить
их
и
(
–
в момент времени
;
–
в момент
с)
pис. 1.4.
Исключив параметр
из уравнений, получим
.
Так как
,
то
это уравнение окруж-ности с радиусом
.
При

Рис.
1.4
При
с,
а
(м),
,
.
;
,
так как
.
2. Для
момента времени
определить и построить на чертеже:
скорость точки
:
,
(м/с),
(м/с),
,
модуль вектора
скорости.
Направляющие косинусы
вектора скорости:
,
,
.
ускорение точки
:
,
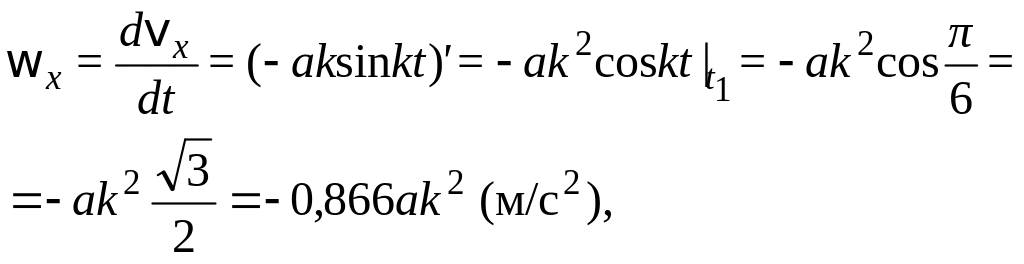
.
Модуль вектора
ускорения точки
:
.
Направляющие косинусы
вектора ускорения точки:
,
,
.
3. Определить
касательное и нормальное ускорения
точки
,
постоянные
величины;
,
.
Полное ускорение
точки
равно нормальному ускорению, так как
скорость по величине постоянна:
.
4. Определить
характер движения точки: точка
движется по окружности равномерно!
5. Определить
радиус кривизны траектории точки в
момент
:
нормальное ускорение;
отсюда
радиус окружности
траектории точки
.
З
А Д А Н И Е К2
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
26.03.2015235.52 Кб14km.doc
- #
- #
- #
- #