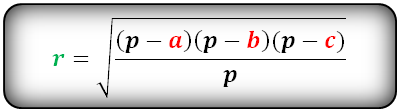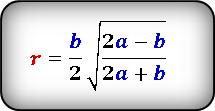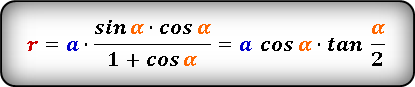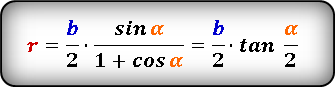Как найти радиус наименьшего круга треугольника

Нахождение радиуса описанной вокруг треугольника окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

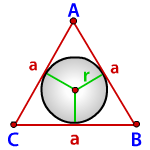
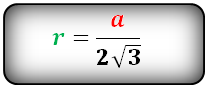
Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

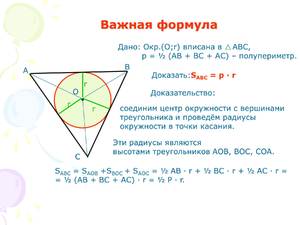
Формула радиуса окружности, вписанной в треугольник

Если окружность располагается внутри угла и касается его сторон, её называют вписанной в этот угол. Центр такой вписанной окружности располагается на биссектрисе этого угла.

Если же она лежит внутри выпуклого многоугольника и соприкасается со всеми его сторонами, она называется вписанной в выпуклый многоугольник.

Окружность, вписанная в треугольник

Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.

Радиус такой окружности будет зависеть от следующих параметров треугольника:

  1. Длин сторон треугольника.
  2. Его площади.
  3. Его периметра.
  4. Величины углов треугольника.

Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.

Вычисление с помощью полупериметра

Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:

  1. Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
  2. Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
  3. В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
  4. Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
  5. Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).

Вычисление с учётом площади треугольника

Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.

  1. Для начала нужно удвоить величину площади.
  2. Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
  3. Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.

Расчёт с помощью тригонометрических функций

Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:

r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.

Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.

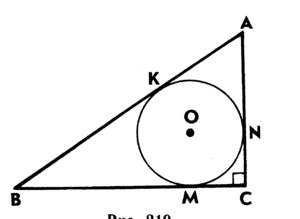
Окружность, вписанная в прямоугольный треугольник

В прямоугольный треугольник можно вписать только одну окружность. Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.

  1. Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b, а гипотенуза — переменной с.
  2. Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
  3. Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ, во втором случае применяют теорему косинусов с=a/cosCBA.
  4. Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
  5. Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем —величина полупериметра.

Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.

Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.

Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.

Видео

Из этого видео вы узнаете, как находить радиус вписанной в треугольник окружности.

Все формулы для радиуса вписанной окружности

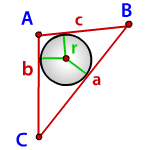
Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

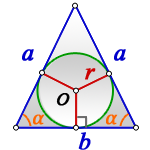
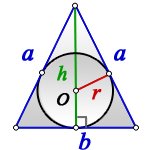
Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

источники:

http://liveposts.ru/articles/education-articles/matematika/formula-radiusa-okruzhnosti-vpisannoj-v-treugolnik

http://www-formula.ru/2011-09-24-00-40-48

Источник

�������

��� ����������� �� ��������� 2, 3, 4.
������� ������ ����������� �����,
�� �������� ����� �������� ���� �����������.

���������

��� �� ������ ��������� ����� ������������ ����������.

�������

�������, ��� ���� ����������� — ������������.
������� �� ���������� � ����������, ����������� �� ����������
�������, ��� �� �������� (������ ���� ���������� ����� 2).
� ������ �������, �� ����� �������, �������� 2, ������ ��������
������ �����������, ��������� ������� ����� 4 ������ ���� ��
������ �������� �����.

�����

2.00

��������� � ���������� �������������

Источник

Решение

Найдём с помощью теоремы косинусов косинус наибольшего угла $ alpha$ данного треугольника:

cos$displaystyle alpha$ = $displaystyle {frac{7^{2} + 9^{2} - 12^{2}}{2cdot 7cdot 9}}$ = — $displaystyle {textstylefrac{1}{9}}$ < 0.

Значит, этот треугольник — тупоугольный. Следовательно, круг, построенный на его большей стороне (равной 12) как на диаметре, содержит этот треугольник.


Ответ

6.

Источник

2021-07-22   comment

Найдите радиус наименьшего круга, в котором можно разместить треугольник со сторонами 7, 9 и 12.

Решение:

Найдём с помощью теоремы косинусов косинус наибольшего угла $alpha$ данного треугольника:

$cosalpha=frac{7^{2}+9^{2}-12^{2}}{2cdot7cdot9}=-frac{1}{9}lt0.$

Значит, этот треугольник — тупоугольный. Следовательно, круг, построенный на его большей стороне (равной 12) как на диаметре, содержит этот треугольник (см. задачу 5370).

Источник
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284

#include <cassert>
#include <cstdlib>
#include <cmath>
#include <limits>
#include <vector>
#include <compare>
#include <algorithm>
#include <iomanip>
#include <iostream>
#include <ctime>
 
using Xy = double;
using Xy2 = double;
using Angle = double;
 
constexpr Xy XY_EPS = 0.000001;
 
struct Point
{
  Xy x, y;
 
  Point() : x(0), y(0)
    {}
 
  Point(Xy x, Xy y) : x(x), y(y) 
    {}
 
  Xy2 radius2() const
    { return x * x + y * y; }
 
  Xy radius() const
    { return (Xy) std::sqrt(radius2()); }
 
  Point cw() const
    { return { y, -x }; }
 
  Point ccw() const
    { return { -y, x }; }
 
  bool is_zero() const
    { return std::abs(x) <= XY_EPS && std::abs(y) <= XY_EPS; }
 
  Point operator /(Xy rhs) const
    { return { x / rhs, y / rhs }; }
 
  friend Point operator +(const Point& lhs, const Point& rhs)
    { return { lhs.x + rhs.x, lhs.y + rhs.y }; }
 
  friend Point operator -(const Point& lhs, const Point& rhs)
    { return { lhs.x - rhs.x, lhs.y - rhs.y }; }
 
  friend Xy2 operator *(const Point& lhs, const Point& rhs)
    { return lhs.x * rhs.x + lhs.y * rhs.y; }
 
  friend Xy2 cp(const Point &lhs, const Point &rhs)
    { return lhs * rhs.cw(); }
                                                       
  friend Xy distance(const Point& a, const Point& b)
    { return (a - b).radius(); }
 
  friend auto operator <=>(const Point &, const Point &) = default;
 
  friend bool eq_abs(const Point &lhs, const Point &rhs)
    { return (rhs - lhs).is_zero(); }
 
  friend std::ostream& operator <<(std::ostream& lhs, const Point& rhs)
    { return lhs << std::setw(4) << rhs.x << ", " << std::setw(4) << rhs.y; }
 
  static const Point ZERO, INF; 
};
 
const Point Point::ZERO(0, 0);
const Point Point::INF(std::numeric_limits<Xy>::max(), std::numeric_limits<Xy>::max());
 
Point intersect(const Point& a1, const Point& b1, const Point& a2, const Point& b2)
{
  assert(!eq_abs(a1, b1) && !eq_abs(a2, b2));
 
  Xy2 cp1 = cp(a1, b1), cp2 = cp(a2, b2);
  Point v1 = a1 - b1, v2 = a2 - b2;
 
  Xy2 den = cp(v1, v2);
  if (std::abs(den) <= XY_EPS)
    return Point::INF;
 
  return { (Xy) ((cp1 * v2.x - cp2 * v1.x) / den), (Xy) ((cp1 * v2.y - cp2 * v1.y) / den) };
}
 
int turn(const Point &a, const Point &b, const Point &c)
{ // Left turn = +1, right turn = -1 
  Point ab = b - a, bc = c - b;
  Xy2 area = cp(ab, bc);
  return (area > 0) - (area < 0);
}
 
Angle neg_cos(const Point &a, const Point &b, const Point &c)
{
  Point va = a - b, vc = c - b;
  if (va.is_zero() || vc.is_zero())
    return 1.0; // -cos(PI)
  return -(Angle) (va * vc) / (va.radius() * vc.radius());
}
 
//////////////////////////////////////////////////////////////////////////////////////////
 
struct Circle
{
  Point o;
  Xy r;
 
  Circle() = default;
 
  Circle(const Point& o, Xy r = 0) : o(o), r(r)
    {}
 
  Circle(const Point &a, const Point &b) : Circle((a + b) / 2, distance(a, b) / 2)
    {}
 
  Circle(const Point &a, const Point &b, const Point &c)
  {
    assert(!eq_abs(a, b) && !eq_abs(b, c) && !eq_abs(a, c));
    Point mab1 = (a + b) / 2, mbc1 = (b + c) / 2;
    Point mab2 = mab1 + (b - a).ccw(), mbc2 = mbc1 + (c - b).ccw();
    o = intersect(mab1, mab2, mbc1, mbc2);
    r = distance(o, c);
  }
 
  bool contains(const Point& p) const
    { return r >= 0 && (p - o).radius2() <= r * r; }
 
  friend std::ostream& operator <<(std::ostream& lhs, const Circle& rhs)
    { return lhs << "o = " << rhs.o << ", r = " << rhs.r; }
};
 
Circle circle(const Point &a, const Point &b, const Point &c)
{
  if (eq_abs(a, b) || eq_abs(b, c))
    return Circle(a, c);
  else if (eq_abs(a, c))
    return Circle(a, b);
  else
    return Circle(a, b, c);
}
 
//////////////////////////////////////////////////////////////////////////////////////////
 
using Points = std::vector<Point>;
 
//////////////////////////////////////////////////////////////////////////////////////////
// Convex hull
 
Points convex_hull(Points points)
{
  auto chain_vertex = [](Points &chain, const Point &p, int good_turn)
  {
    while (chain.size() > 1)
    {
      Points::iterator it_b = std::prev(chain.end()), it_a = std::prev(it_b);
      if (turn(*it_a, *it_b, p) == good_turn)
        break;
 
      chain.pop_back();
    }
 
    chain.push_back(p);
  };
 
  std::sort(points.begin(), points.end());
 
  Points lower_chain, upper_chain;
 
  for (const Point &p : points)
  {
    chain_vertex(lower_chain, p, +1);
    chain_vertex(upper_chain, p, -1);
  }
 
  lower_chain.insert(lower_chain.end(), 
    std::next(upper_chain.rbegin()), std::prev(upper_chain.rend()));
  return lower_chain;
}
 
//////////////////////////////////////////////////////////////////////////////////////////
// Smallest enclosing circle
 
struct Ra
{
  Circle circle;
  Angle angle; // negative cosine
 
  Ra() : 
    circle(Point::ZERO, std::numeric_limits<Xy>::lowest()), 
    angle(std::numeric_limits<Angle>::lowest())
    {}
 
  Ra(const Point &a, const Point &b, const Point &c) : 
      circle(a, b, c), angle(neg_cos(a, b, c))
    {}
 
  bool is_non_obtuse() const
    { return angle <= 0; }
 
  friend std::strong_ordering operator <=>(const Ra &lhs, const Ra &rhs)
  {
    if (auto cmp = std::strong_order(lhs.circle.r, rhs.circle.r); cmp != 0)
      return cmp;
 
    if (auto cmp = std::strong_order(lhs.angle, rhs.angle); cmp != 0)
      return cmp;
 
    return std::strong_ordering::equal;
  }
};
 
Circle smallest_enclosing_circle(Points points)
{
  assert(!points.empty());
 
  Points::size_type n = points.size();
  if (n <= 2)
    return n == 1 ? Circle(points[0], 0) : Circle(points[0], points[1]);
 
  points.push_back(points[0]);
  points.push_back(points[1]);
 
  for (; n > 2; --n)
  {
    assert(points.size() == n + 2 && points[n] == points[0] && points[n + 1] == points[1]);
 
    Ra ra_max;
    Points::size_type i_max = 0;
 
    for (Points::size_type i = 1; i <= n; ++i)
      if (Ra ra(points[i - 1], points[i], points[i + 1]); ra > ra_max)
      {
        ra_max = ra;
        i_max = i;
      }
 
    assert(i_max != 0);
    if (ra_max.is_non_obtuse())
      break;
 
    assert(n >= 3);
 
    if (i_max == 1)
    { // Erase [1] and update [n + 1]
      points[n + 1] = points[2];
      points.erase(points.begin() + 1);
    }
    else if (i_max == n)
    { // Erase [0] and update [n] and [n + 1]
      points[n] = points[1];
      points[n + 1] = points[2];
      points.erase(points.begin());
    }
    else
      // Erase [i_max]
      points.erase(points.begin() + i_max);
  }
 
  return n == 2 ? Circle(points[0], points[1]) : Circle(points[0], points[1], points[2]);
}
 
//////////////////////////////////////////////////////////////////////////////////////////
 
int main()
{
  std::srand((unsigned) std::time(NULL));
 
  Points s;
 
  for (unsigned n = 40; n > 0; --n)
  {
    Point p(rand() % 600 - 300, rand() % 600 - 300);
    std::cout << p << std::endl;
    s.push_back(p);
  }
 
  s = convex_hull(s);
  Circle c = smallest_enclosing_circle(s);
 
  std::cout << std::endl << c << std::endl;
}
Источник

Понравилась статья? Поделить с друзьями:
  • Как найти тумане цветы геншин
  • Как составить задачу по физике по теме масса 7 класс
  • Как найти фото с интернета или нет
  • Абсолютная шкала как найти
  • Как найти отделение сбербанка по его номеру