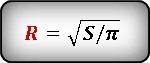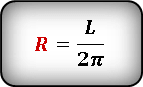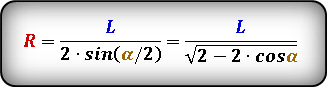Как найти радиус окружности через длину хорды

Как найти радиус по хорде

Хорда — это отрезок, соединяющий две точки окружности. Пусть длина хорды известна. Тогда, если также известен угол между радиусами, проведенными в концы хорды, то можно найти и радиус окружности.

Вам понадобится

• Транспортир, линейка.

Инструкция

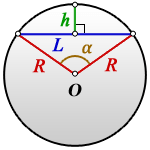
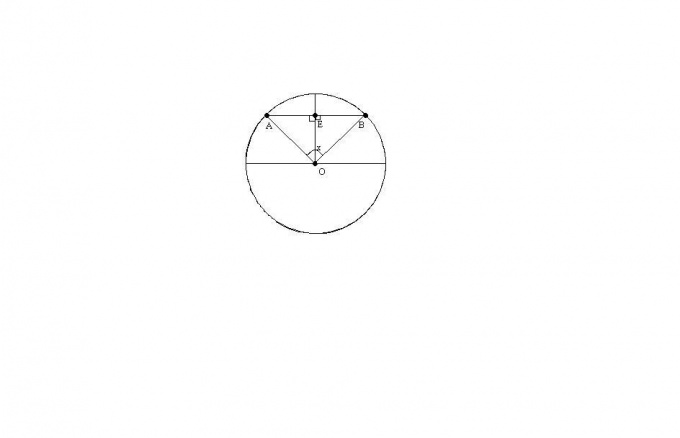
Пусть известны длина хорды AB и угол AOB между радиусами, проведенными в концы хорды. Найдем по этим данным радиус окружности с центром в точке O.

Треугольник AOB — равнобедренный, так как OA = OB = R. По свойству равнобедренного треугольника высота OE одновременно является его медианой и биссектрисой угла AOB. Обозначим угол AOB за х.
Треугольник AEO — прямоугольный с прямым углом AEO. Так как высота ОЕ также является биссектрисой угла AOB, то угол AOE = x/2. Тогда из прямоугольного треугольника AOE имеем: OA = R = (AB/2)/sin(x/2).

Все основные формулы для определения длины радиуса окружности

Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

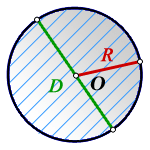
R — радиус окружности (круга)

D — диаметр, D = 2 R

Формула для определения длины радиуса, если известна площадь круга :

Калькулятор для расчета длины радиуса через площадь

Формула для определения длины радиуса, если известна длина окружности :

Калькулятор для расчета длины радиуса через длину окружности

R — радиус окружности (круга)

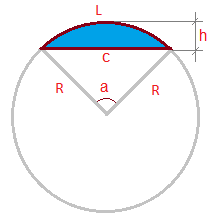
h — высота сегмента

α — центральный угол

Формула для определения длины радиуса, если известна длина хорды :

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды	Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности	Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Однако, как справедливо заметил наш пользователь:«на практике hourто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента, вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Все основные формулы для определения длины радиуса окружности

Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

R — радиус окружности (круга)

D — диаметр, D = 2 R

Формула для определения длины радиуса, если известна площадь круга :

Калькулятор для расчета длины радиуса через площадь

Формула для определения длины радиуса, если известна длина окружности :

Калькулятор для расчета длины радиуса через длину окружности

R — радиус окружности (круга)

h — высота сегмента

α — центральный угол

Формула для определения длины радиуса, если известна длина хорды :

Калькулятор для расчета длины радиуса через длину хорды

Подробности Автор: Сергей Кондратов Опубликовано: 07 сентября 2011 Обновлено: 13 августа 2021

Найти радиус

Здравствуйте! Можно ли найти радиус окружности по длине хорды и дуги? или нужны дополнительные данные?

Лучший ответ по мнению автора

Александр

ВОПРОС:

Здравствуйте! Можно ли найти радиус окружности по длине хорды и дуги? или нужны дополнительные данные?

ОТВЕТ:

Ничего дополнительного не нужно, решение задачи изложено ниже.

РЕШЕНИЕ:

Разделим исходный сектор круга, ограниченного центром круга и концами хорды, на два одинаковых, проведя биссектрису центрального угла. Будем рассматривать далее один из них (любой из двух полученных) и соответствующий прямоугольный треугольник (с вершинами в центре круга, одним из концов хорды и её серединой).

Пусть, далее, α – острый угол этого треугольника с вершиной в центре круга, a – длина противолежащей стороны (катета) этого треугольника, b — длины соответствующей дуги окружности, r – её радиус (искомый). Отметим также, что a и b – заданные величины, равные половине длин исходных хорды и дуги соответственно.

Тогда, очевидно (из чисто геометрического рассмотрения), имеем:

Это, по сути, запись двух определений: (1) – для длины дуги, (2) – для синуса угла. Таким образом, имеем систему двух уравнений с двумя неизвестными (α и r). Явного (аналитического) решения она не имеет – возможно лишь численное решение (которое существует и единственно). Решать эту задачу в каждом конкретном случае – при заданных численных значениях a и b (точнее, как отмечено выше, – 2a и 2b) – можно двумя способами: «школьным» (геометрическим) и каким-либо численным методом.

«Школьный» метод:

После несложных преобразований уравнения (1) и (2) можно переписать, например, в виде:

где k = a/b. После этого строим графики функций f1(α) = kα, f2(α) = sin α и находим точку их пересечения, что соответствует решению уравнения (2′).

Отметим, что это пересечение (т.е. решение задачи) существует и единственно (и находится «недалеко» от начала координат): оба графика проходят через начало координат, причем второй (синусоида) выходит из начала координат под углом π/4 (=45o), первый (прямая) – под меньшим углом (поскольку k = a/b < 1, т.к. a < b – хорда должна быть короче дуги).

Таким образом, из графика находим α, а затем, используя уравнение (1′), и искомое значение радиуса r.

Численный метод:

Типичное численное решение такой задачи – каким-либо итерационным методом, например, методом Ньютона: дифференцируем и линеаризуем (по α) уравнение (2′), задаём какое-нибудь начальное приближение αo для α (наиболее логично и просто взять αo = 0) и дальше итерационно находим решение α = α* с любой наперед заданной точностью. Далее, подставляя в уравнение (1′) найденное значение угла α*, находим искомое значение радиуса r.

Можно чуть по-другому – чтобы сразу решать уравнение (задачу) относительно радиуса r (без промежуточного нахождения угла α = α*). Для этого, например, просто подставляем из (1) (или из (1′)) выражение для угла α = b/r в уравнение (2′), получив тогда уравнение относительно переменной r.

Далее также как и выше дифференцируем, линеаризуем (но уже не по α, а по r) и решаем полученное уравнение и задачу в целом.

Научный форум dxdy

Найти радиус окружности по длине дуги и хорде

На одном из форумов попался вопрос, содржащий «школьную» задачку. Дано: Длина дуги части окружности , а длина хорды, на которую опирается эта дуга равна . Найти радиус окружности.

Вначале, все было хорошо и просто. Провел радиус из центра к концу дуги , а так же радиус, перпендикулярный хорде
, который пересек хорду в точке , образуя прямоугольный треугольник . Катет .
Угол при вершине O обозначил как . По определению синуса получил, что
или (1)
А из формулы длины дуги, получил или (2)
(2x потому, что — половина центрального угла рассматирваемой дуги).

Подстставляем в (1) вместо выражение, полученное из (2): или
, где

Ну, вот тут и заминочка вышла. Как найти по заданному ?
На практике, конечно нет проблем. В зависимости от точности либо найти значение графически, либо использовать один
из приближенных методов. Но возникает вопрос, есть ли аналитическое решение? Т.е. можно ли выразить через
элементарные функции от . Причем, функция интересует нас только при от 0 до пи.

Есть предположение, что это невозможно. Так ли это? Можно ли это доказать?