Вневписанные окружности
Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.
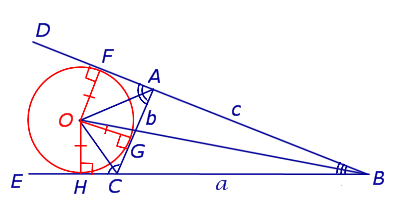
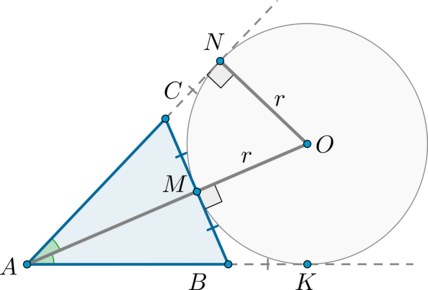
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).
Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:
Следовательно, справедливо равенство
Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства
откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .
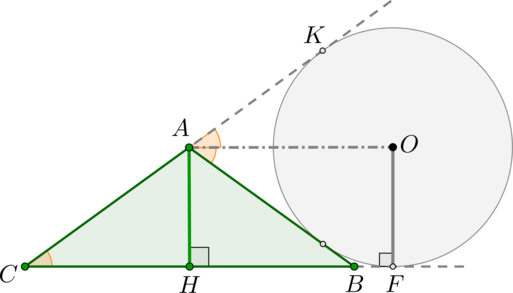
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).
Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.
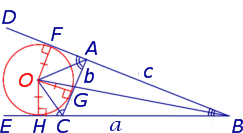
Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом rb .
Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство
где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:
где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.
Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле
где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .
Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства
Следовательно, справедливо равенство
что и требовалось доказать.
Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:
Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:
Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

что и требовалось доказать.
Теорема 5 . Площадь треугольника можно вычислить по формуле
Доказательство . Перемножим формулы
что и требовалось доказать.
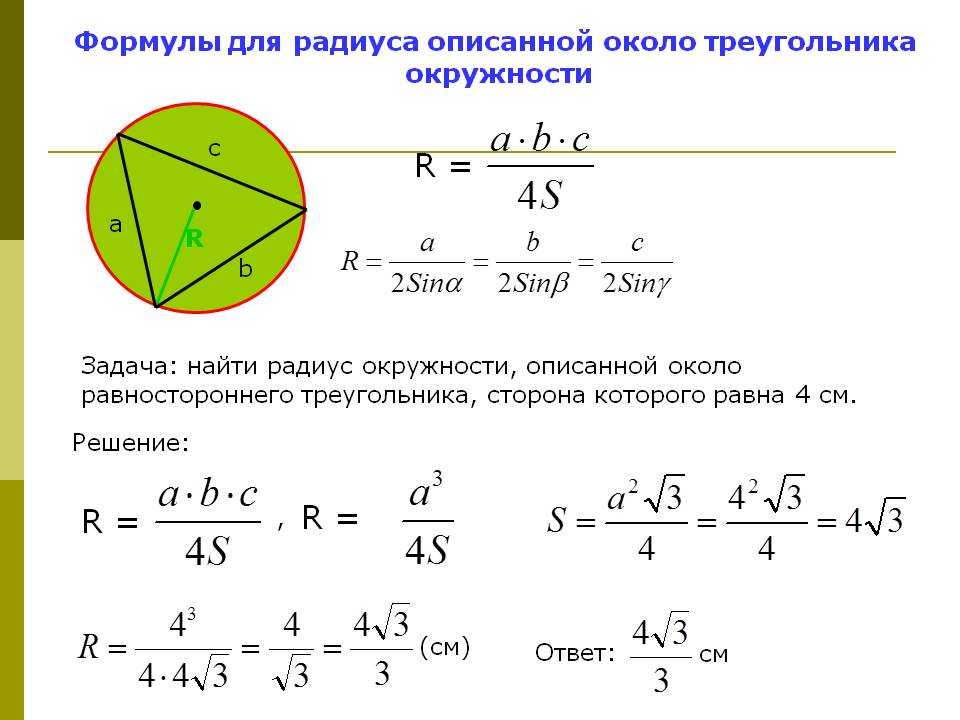
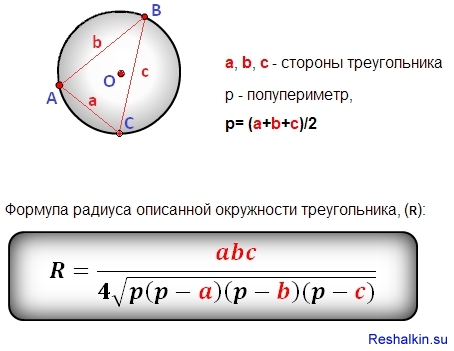
Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:
Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим
Преобразуем выражение, стоящее в квадратной скобке:
Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Радиус — что это такое и как найти радиус окружности
Через длину стороны
Формула для нахождения длины окружности через радиус:
, где r — радиус окружности.
Найти радиус круга, зная окружность
Окружность круга P
Результат
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.
Вычисление радиуса
Радиус можно посчитать разными способами.
Если известен диаметр
Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:
Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:
В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
Способ расчета радиуса круга:
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Как посчитать радиус зная длину окружности
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
По площади сектора и центральному углу
- Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем
В случае, когда величина α выражена в в радианах , получаем
Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Центральный угол, вписанный угол и их свойства
Связанные определения
- Центральный угол в окружности — это угол , образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .
В случае, когда величина α выражена в градусах , справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах , справедлива пропорция
из которой вытекает равенство:
Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
| < | x = a + r cos t |
| y = b + r sin t |
Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Основные свойства касательных к окружности
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
Обобщения
Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Площадь круга, онлайн расчет
Как найти площадь круга по формуле через радиус либо диаметр круга.
Площадь круга, онлайн расчет
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.
Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
http://exceltut.ru/radius-chto-eto-takoe-i-kak-najti-radius-okruzhnosti/
Сообщения без ответов | Активные темы
Найти радиус окружности,касающейся двух сторон треугольника
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
lextor |
Заголовок сообщения: Найти радиус окружности,касающейся двух сторон треугольника
|
||
|
Здраствуйте. Прошу помощь в решении задачи.
|
||
| Вернуться к началу |
|
||
|
lextor |
Заголовок сообщения: Re: Найти радиус окружности,касающейся двух сторон треугольника
|
|
По св-ву получается биссектриса делит сторону на 7целых 6/27 и 7целых 21/27. Что дальше?
|
|
| Вернуться к началу |
|
|
lextor |
Заголовок сообщения: Re: Найти радиус окружности,касающейся двух сторон треугольника
|
|
Спасибо большое. А можно узнать как вы вывели эту формулу?
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Даны уравнения двух сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
Nino |
8 |
1037 |
07 ноя 2013, 07:59 |
|
Найдите радиус окружности, описанной около треугольника
в форуме Геометрия |
golden cat |
2 |
123 |
11 май 2022, 19:04 |
|
Найдите радиус окружности, описанной около треугольника
в форуме Геометрия |
Alliance |
11 |
1399 |
08 апр 2014, 09:33 |
|
Найти радиус окружности
в форуме Аналитическая геометрия и Векторная алгебра |
RaysOfTheSun |
4 |
993 |
03 апр 2019, 13:25 |
|
Найти радиус окружности
в форуме Геометрия |
kicultanya |
7 |
494 |
06 ноя 2016, 12:57 |
|
Найти радиус окружности
в форуме Геометрия |
wastelander |
3 |
160 |
27 фев 2020, 12:35 |
|
Найти уравнения сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
yol145 |
19 |
1273 |
10 ноя 2015, 16:34 |
|
Найти уравнения сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
andreta |
16 |
2101 |
22 дек 2013, 22:41 |
|
Найти длины сторон треугольника
в форуме Геометрия |
MathSamurai |
6 |
258 |
15 янв 2022, 17:40 |
|
Найти радиус вписанной в треугольник окружности
в форуме Геометрия |
Fajarovich |
3 |
686 |
22 сен 2013, 18:17 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
|
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см. Достраиваем ещё один радиус: на моём рисунке он обозначен красным отрезком. Ка известно из геометрии: Радиус между касательной АВ и секущей AO, образует катет прямоугольного треугольника ОВА. Находим этот катет по теореме Пифагора: Катет равен корню квадратному из разности квадрата гипотенузы и квадрату второго катета. Решение: Мой ответ: 5 автор вопроса выбрал этот ответ лучшим Валерий Альбертович 3 года назад Касательная AB и секущая AO образуют прямоугольный треугольник AOB (для этого соединим точки O и B). Прямая OB и будет радиусом окружности, который там нужно найти. Так как треугольник прямоугольный (угол B = 90 градусов), можем найти сторону OB по теореме Пифагора: OB^2 = AO^2-AB^2 = 13^2-12^2 = 169-144 = 25 => OB = 5, а т.к. OB — радиус окружности, следовательно это и есть наш ответ. Ответ: 5 Евгений трохов 3 года назад Радиус ОВ перпендикулярен касательной АВ.Треугольник АОВ прямоугольный.АО-гипотенуза.АВ-один катет.ОВ-радиус и другой катет одновременно. AO^2=AB^2+OB^2 OB^2=AO^2-AB^2=13^2-12^2=169-144=25 OB=5. Ответ: радиус =5 Знаете ответ? |
16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с окружностями (страница 2)
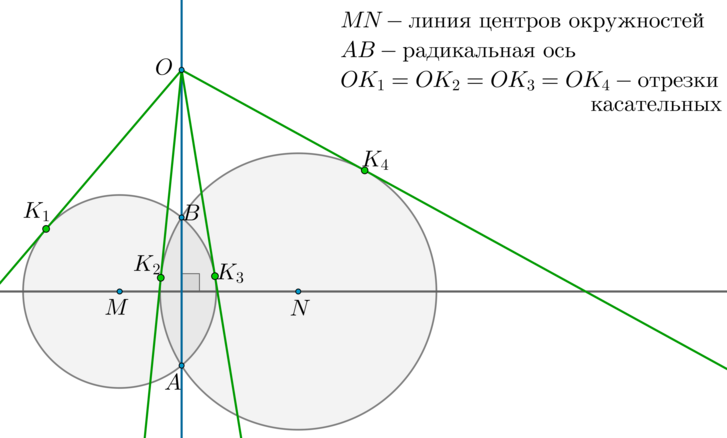
(blacktriangleright) Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Радикальная ось перпендикулярна линии центров окружностей. Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
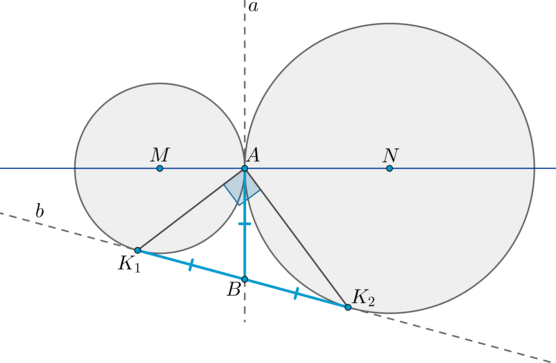
(blacktriangleright) Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A). Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B). Точки касания — точки (A, K_1, K_2). Тогда [{large{K_1B=AB=K_2B}}] [{large{angle K_1AK_2=90^circ}}]
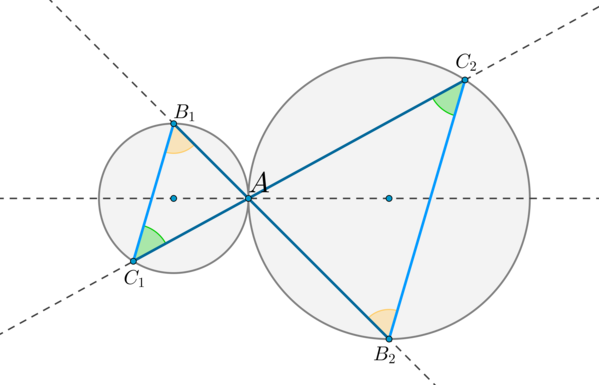
(blacktriangleright) Пусть две окружности касаются внешним образом в точке (A). Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2), пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [{large{triangle AB_1C_1 sim triangle
AB_2C_2}}] [{large{B_1C_1parallel B_2C_2}}]
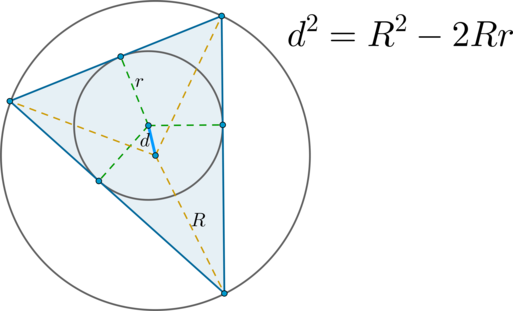
(blacktriangleright) Формула Эйлера: Пусть (R) — радиус описанной около треугольника окружности, (r) — радиус вписанной окружности. Тогда расстояние между центрами этих окружностей вычисляется по формуле:
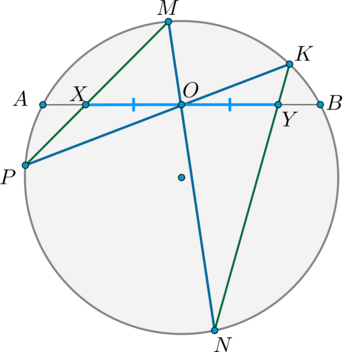
(blacktriangleright) Теорема о бабочке: Пусть через середину хорды (AB) — точку (O), проведены две хорды (MN) и (KP). Пусть (MPcap AB=X, KNcap AB=Y). Тогда [{large{OX=OY}}]
Задание
8
#2387
Уровень задания: Легче ЕГЭ
Окружность касается стороны (BC=15) и продолжений сторон (AB=AC=8,5) треугольника (ABC). Найдите радиус этой окружности.
Заметим, что треугольник (ABC) равнобедренный. Т.к. центр окружности равноудален от сторон угла (A), то он лежит на биссектрисе этого угла (то есть (AO) – биссектриса (angle A)). Т.к. треугольник равнобедренный, то биссектриса (AO) является также медианой и высотой, следовательно, т.к. (OMperp BC) ((M) – точка касания), то точка (M) лежит на отрезке (AO).
(triangle ACMsim triangle ANO) по двум углам. Следовательно,
[dfrac{CM}{ON}=dfrac{AC}{AO} quad Rightarrow quad
dfrac{frac{15}2}r=dfrac{8,5}{AM+r}]
Таким образом, для того, чтобы найти (r), нужно сначала найти (AM).
По теореме Пифагора из (triangle AMC): (AM^2=AC^2-MC^2=8,5^2-7,5^2=16), следовательно, (AM=4). Значит:
[dfrac{frac{15}2}{r}=dfrac{8,5}{4+r} quad Rightarrow quad r=30.]
Ответ: 30
Задание
9
#2388
Уровень задания: Легче ЕГЭ
Окружность касается стороны (AB) и продолжения сторон (BC) и (AC) треугольника (ABC), причем (AB=AC=17), (BC=30). Найдите радиус этой окружности.
Т.к. окружность вписана в угол (BAK), то ее центр лежит на его биссектрисе, следовательно, (AO) – биссектриса (angle BAK). Обозначим (angle BAO=angle KAO=alpha). Тогда (angle
BAC=180^circ-2alpha). Т.к. (triangle ABC) – равнобедренный, то с другой стороны (angle BAC=180^circ-2angle B=180^circ-2angle C). Таким образом, (angle B=angle C=alpha).
Следовательно, (angle ACB=angle KAO) как соответственные при прямых (CB) и (AO) и секущей (CA). Следовательно, по признаку (CBparallel AO).
Проведем (AHperp BC). Т.к. (triangle ABC) – равнобедренный, то (AH) – медиана.
Имеем: (AH=OF) как отрезки перпендикулярных прямых, заключенные между параллельными прямыми (BC) и (AO). А (AH) можно найти по теореме Пифагора из (triangle AHB):
[AH^2=AB^2-HB^2=17^2-15^2=8^2 quad Rightarrow quad r=OF=AH=8.]
Ответ: 8
Задание
10
#2386
Уровень задания: Легче ЕГЭ
В треугольнике со сторонами (a,b,c) радиус вписанной окружности равен (r=frac{a+b-c}2). Докажите, что треугольник является прямоугольным.
Как известно, площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. С другой стороны, площадь можно найти по формуле Герона. Следовательно:
[S=sqrt{p(p-a)(p-b)(p-c)}=pcdot r quad Rightarrow quad
(p-a)(p-b)(p-c)=pcdot r^2]
Т.к. (p=dfrac{a+b+c}2), (r=dfrac{a+b-c}2), то
(dfrac{a+b-c}2cdot dfrac{a+c-b}2cdot
dfrac{b+c-a}2=dfrac{a+b+c}2cdot dfrac{(a+b-c)^2}4 quad
Rightarrow )
(Rightarrow quad (c+(a-b))(c-(a-b))=((a+b)+c)((a+b)-c) quad
Rightarrow quad c^2-(a-b)^2=(a+b)^2-c^2)
(Rightarrow quad c^2-a^2+2ab-b^2=a^2+2ab+b^2-c^2 quad
Rightarrow quad c^2=a^2+b^2)
Таким образом, по обратной теореме Пифагора треугольник будет прямоугольным, причем прямой угол находится против стороны (c).
Ответ:
Доказательство
Задание
11
#2437
Уровень задания: Равен ЕГЭ
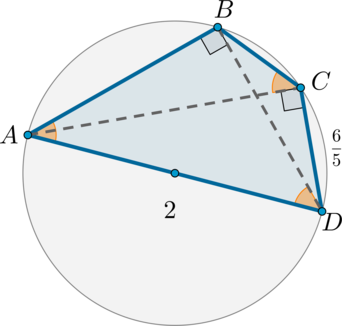
Четырехугольник (ABCD) вписан в окружность, причем (angle
ACD=90^circ), (angle ACB=angle BAD), (AD=2), (CD=frac65).
Найдите длину отрезка (BC).
1) Т.к. (angle ACD=90^circ), то он опирается на диаметр, то есть (AD) – диаметр. Следовательно, (angle ABD=90^circ).
Вписанные углы (angle ACB) и (angle ADB) равны, т.к. опираются на одну и ту же дугу. Следовательно, (triangle ABD) – прямоугольный и равнобедренный, то есть (angle BDA=angle BAD=45^circ) и (AB=BD=ADdivsqrt2=sqrt2).
2) По теореме Пифагора из (triangle ACD):
[AC=sqrt{AD^2-CD^2}=sqrt{4-frac{36}{25}}=dfrac85]
Тогда по теореме косинусов из (triangle ABC):
[AB^2=AC^2+BC^2-2cdot ACcdot BCcdot cos45^circ quad Rightarrow quad
2=dfrac{64}{25}+BC^2-2cdot dfrac85cdot BCcdot dfrac{sqrt2}2]
Решая полученное квадратное уравнение, находим, что (BC=dfrac{sqrt2}5) или (BC=dfrac{7sqrt2}5).
Заметим, что в (triangle ABC) угол (B) – тупой, следовательно, против него должна лежать большая сторона. Таким образом, число (dfrac{7sqrt2}5) не подходит, т.к. (dfrac{7sqrt2}5>dfrac85=AC).
Таким образом, (BC=dfrac{sqrt2}5).
Ответ:
(dfrac{sqrt2}5)
Задание
12
#2449
Уровень задания: Равен ЕГЭ
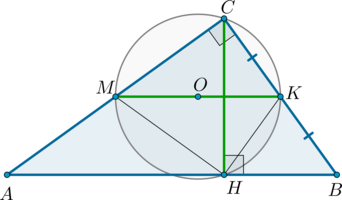
Найдите радиус окружности, проходящей через вершину (C) прямого угла треугольника (ABC), основание (H) высоты (CH) и точку (K) — середину катета (BC), если гипотенуза треугольника равна (c).
Сразу заметим, что (angle C=90^circ) — вписанный угол, следовательно, он опирается на диаметр. Значит, если (M) – точка пересечения окружности с катетом (AC), то (MK) – диаметр.
Заметим, что в (triangle CHB) (HK) — медиана, проведенная из вершины прямого угла, следовательно, она равна половине гипотенузы, то есть (HK=KC).
Таким образом, прямоугольные треугольники (MCK) и (MHK) ((angle H=90^circ), т.к. опирается на диаметр) равны по катету и гипотенузе. Значит, (KM) – содержит биссектрису (angle
CKH), а т.к. (triangle CKH) равнобедренный, то и высоту, то есть (KMperp CH).
По условию также (CHperp AB), следовательно, (MKparallel AB). Значит, по теореме Фалеса (M) – также середина катета (AC), то есть (MK) – средняя линия.
Значит, радиус окружности равен [R=dfrac12 MK=dfrac12cdot dfrac12AB=dfrac14c.]
Ответ:
(dfrac c4)
Задание
13
#2450
Уровень задания: Равен ЕГЭ
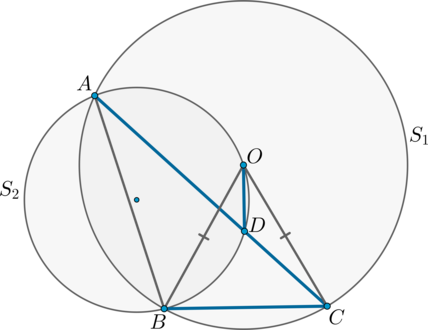
Окружности (S_1) и (S_2) пересекаются в точках (A) и (B), центр (O) окружности (S_1) лежит на окружности (S_2). Хорда (AC) окружности (S_1) пересекает окружность (S_2) в точке (D). Докажите, что отрезки (OD) и (BC) перпендикулярны.
Рассмотрим рисунок:
Проведем дополнительно (OB, OC, AB). Заметим, что (triangle BOC) равнобедренный, следовательно, необходимо доказать, что прямая (OD) содержит высоту, опущенную к основанию. Докажем, что прямая (OD) содержит биссектрису, тогда отсюда будет следовать утверждение задачи.
Таким образом, необходимо доказать, что (angle BOD=angle COD).
Заметим, что (angle BOD=angle BAD=alpha) как вписанные углы в окружности (S_2), опирающиеся на одну и ту же дугу (buildrelsmileover{BD}).
С другой стороны, (angle BAC) (он же (angle BAD)) — вписанный угол в окружности (S_1), опирающийся на дугу (buildrelsmileover{BC}), следовательно, (buildrelsmileover{BC}=2angle BAC=2alpha).
(angle BOC) — центральный угол в окружности (S_1), опирающийся на дугу (buildrelsmileover{BC}), следовательно, (angle
BOC=buildrelsmileover{BC}=2alpha).
Отсюда (angle COD=angle BOC-angle BOD=2alpha-alpha=alpha). Следовательно, (OD) – часть биссектрисы равнобедренного треугольника (BOC), а следовательно, и часть высоты, чтд.
Ответ:
Доказательство
Задание
14
#2472
Уровень задания: Равен ЕГЭ
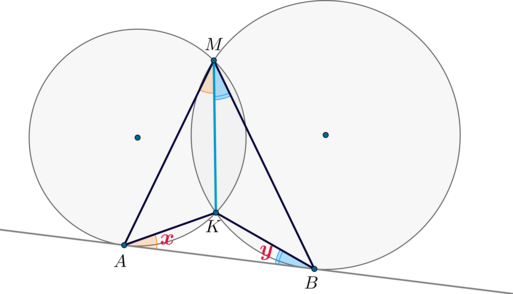
К двум окружностям, пересекающимся в точках (M) и (K), проведена общая касательная. Докажите, что если (A) и (B) – точки касания, то (angle AMB+angle AKB=180^circ).
Обозначим за (x) угол (KAB), за (y) — угол (KBA). Т.к. это углы между касательной (AB) и хордами (AK) и (BK) соответственно, то каждый из них половине дуги, заключенной между касательной и соответствующей хордой, то есть
[begin{aligned} &x=angle KAB=0,5cdotbuildrelsmileover{AK}\
&y=angle KBA=0,5cdotbuildrelsmileover{BK}end{aligned}]
Заметим, что (angle AMK) – вписанный, опирающийся на (buildrelsmileover{AK}), следовательно, (angle AMK=x). Аналогично (angle BMK=y).
Таким образом, (angle AMB=x+y).
Из (triangle AKB): [angle AKB+x+y=180^circ quad Rightarrow
quad angle AKB+angle AMB=180^circ, text{ чтд.}]
Эта же задача с другим решением представлена в разделе “Задачи, требующие дополнительного построения”.
Ответ:
Доказательство

УСТАЛ? Просто отдохни
как найти через высоту, формула с доказательством
Содержание:
- Окружность, вписанная в треугольник — как найти радиус
-
Свойства вписанной в треугольник окружности
- Первое свойство
- Второе свойство
- Третье свойство
-
Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Как найти через высоту или стороны, примеры решения
Содержание
- Окружность, вписанная в треугольник — как найти радиус
-
Свойства вписанной в треугольник окружности
- Первое свойство
- Второе свойство
-
Третье свойство
-
Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Как найти через высоту или стороны, примеры решения
Окружность, вписанная в треугольник — как найти радиус
Определение
Вписанной в треугольник окружностью называют такую окружность, которая занимает внутреннее пространство геометрической фигуры, соприкасаясь со всеми ее сторонами.
В таком случае грани треугольника представляют собой касательные к этой окружности. Сама геометрическая фигура с тремя углами считается описанной вокруг рассматриваемой окружности.
Источник: people-ask.ru
Свойства вписанной в треугольник окружности
Окружность, которую вписали в треугольник, обладает определенными свойствами. Основные из них можно записать таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Центр окружности, которую вписали в треугольник, совпадает с точкой пересечения биссектрис этой геометрической фигуры.
- Во внутреннее пространство любого треугольника можно вписать лишь одну окружность.
- Формула радиуса окружности, который вписали во многоугольник с тремя углами, будет иметь такой вид:
Источник: people-ask.ru
В представленной формуле радиуса окружности использованы следующие величины:
- S – является площадью треугольника;
- р – представляет собой полупериметр геометрической фигуры;
- a, b, c – являются сторонами треугольника.
Перечисленные свойства необходимо доказать.
Первое свойство
Требуется доказать, что центр окружности, которую вписали в фигуру с тремя углами, совпадает с точкой пересечения биссектрис.
Доказательство построено в несколько этапов:
- Необходимо опустить из центральной точки окружности перпендикулярные прямые OL, OK и OM, которые опускаются на стороны треугольника АВС. Из вершин треугольника следует провести прямые, соединяющие их с центром фигуры OA, OC и OB.
Источник: people-ask.ru
- Далее можно рассмотреть пару треугольников AOM и AOK. Можно отметить, что они являются прямоугольными, так как OM и OK являются перпендикулярами к сторонам AC и AB. Гипотенуза OA является общей для пары этих фигур.
- Исходя из того, что касательная к окружности является перпендикуляром к радиусу, который проведен в точку касания, согласно свойству касательной к окружности, то катеты OМ и OК представляют собой радиусы окружности и, следовательно, равны.
- Согласно полученным утверждениям, можно сделать вывод о равенстве прямоугольных треугольников AOМ и AOК по гипотенузе и катету. Таким образом, углы OAМ и OAК тоже равны. Получается, что OA является биссектрисой угла BAC.
- Аналогично можно доказать, что OC является биссектрисой угла ACB, а OB – биссектрисой угла ABC.
- Таким образом, биссектрисы треугольника совпадают в одной точке, которая представляет собой центр вписанной окружности.
Данное свойство окружности доказано.
Второе свойство
Необходимо представить доказательства свойства окружности, согласно которому в любой треугольник можно вписать окружность, причем только одну.
Доказательство состоит из нескольких этапов:
- Окружность получится вписать в треугольник в том случае, когда существует точка, удаленная на равные расстояния от сторон геометрической фигуры.
- Можно построить пару биссектрис ОА и ОС. Из точки, в которой они пересекаются, необходимо опустить перпендикулярные прямые OK, OL и OM ко всем граням многоугольника с тремя углами ABC.
Источник: people-ask.ru
- Затем следует рассмотреть пару треугольников AOK и AOM.
- Эти фигуры обладают общей гипотенузой АО. Углы OAK и OAM равны, так как OA является биссектрисой угла KAM. Углы OKA и OMA прямые, то есть также равны, так как OK и OM являются перпендикулярами к сторонам AB и AC.
- Исходя из того, что две пары углов равны, можно сделать вывод о равенстве третьей пары AOM и AOK.
- Таким образом, получилось подтвердить равенство треугольников AOK и AOM по стороне AO и двум углам, которые к ней прилегают.
Источник: people-ask.ru
- Удалось определить равенство сторон ОМ и ОК, то есть они удалены на одинаковое расстояние от сторон геометрической фигуры АС и АВ.
- Аналогично можно доказать, что OM и OL равны, то есть равноудалены от граней AC и BC.
- Таким образом, точка равноудалена от сторон треугольника, что делает ее центром окружности, которая вписана в этот многоугольник.
- Аналогичным способом можно определить точку во внутреннем пространстве любой геометрической фигуры с тремя углами, которая будет удалена на равные расстояния от его сторон, и представляет собой центр окружности, вписанной в этот треугольник.
- Исходя из вышесказанного, можно сделать вывод о том, что в любой треугольник можно вписать окружность.
- Необходимо заметить, что центральная точка окружности совпадает с точкой, в которой пересекаются биссектрисы треугольника.
- Можно допустить ситуацию, при которой в геометрическую фигуру с тремя углами можно вписать две и более окружности.
- Необходимо провести три прямые из вершин геометрической фигуры к центральной точке окружности, вписанной в нее, и опустить перпендикулярные прямые к каждой грани треугольника. Таким образом, будет доказано, что рассматриваемая окружность лежит на пересечении биссектрис треугольника, согласно доказательству ее первого свойства.
- Получим совпадение центральной точки окружности и центра первой окружности, которая уже была вписана в этот треугольник, а ее радиус соответствует перпендикуляру, опущенному на сторону треугольника так же, как и в первом случае.
Можно сделать вывод о совпадении этих окружностей.
- Аналогично любая другая окружность, вписанная в геометрическую фигуру с тремя углами, будет совпадать с первой окружностью.
- Таким образом, в треугольник получается вписать лишь одну окружность.
Свойство доказано.
Третье свойство
Требуется доказать, что радиус окружности, которую вписали в геометрическую фигуру с тремя углами, представляет собой отношение площади треугольника к полупериметру:
Источник: people-ask.ru
Кроме того, необходимо представить доказательства следующему равенству:
Источник: people-ask.ru
Доказательство:
Источник: people-ask.ru
- Следует рассмотреть произвольный треугольник АВС, стороны которого соответствуют a, b и c. Для расчета полупериметра данного треугольника целесообразно использовать формулу:
Источник: people-ask.ru
- Центральная точка окружности совпадает с точкой пересечения биссектрис геометрической фигуры с тремя углами.
Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей.
Источник: people-ask.ru
- Исходя из того, что площадь какого-либо треугольника представляет собой половину произведения его основания на высоту, а высота треугольников AOC, COB, BOA рассчитывается, как радиус окружности r, то площади треугольников AOC, COB и BOA можно определить по формулам:
Источник: people-ask.ru
- Далее необходимо представить площадь S геометрической фигуры АВС, как сумму площадей нескольких треугольников:
Источник: people-ask.ru
- Следует отметить, что второй множитель является полупериметром геометрической фигуры с тремя углами АВС, что можно записать в виде равенства:
Источник: people-ask.ru
Источник: people-ask.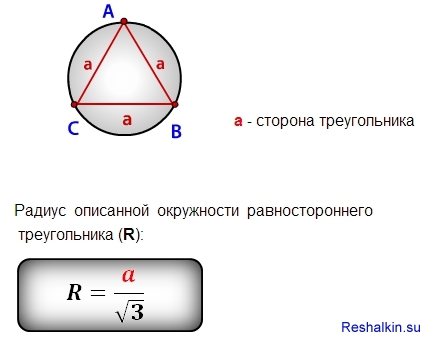
- Таким образом, доказано равенство радиуса вписанной окружности и отношения площади треугольника к полупериметру.
- Можно записать формулу Герона, смысл которой заключается в следующем: площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c)
Источник: people-ask.ru
- Далее следует преобразовать формулу для расчета радиуса:
Источник: people-ask.ru
Свойство окружности доказано.
Формулы вычисления радиуса вписанной окружности
Параметры окружности, которую вписали в геометрическую фигуру с тремя углами, можно рассчитать с помощью стандартных формул. Радиус окружности будет определен в зависимости от типа треугольника.
Произвольный треугольник
Определить радиус окружности, которая вписана в какой-либо треугольник, можно, как удвоенную площадь треугольника, поделенную на его периметр.
Источник: microexcel.ru
В данном случае, a, b, c являются сторонами геометрической фигуры с тремя углами, S – ее площадь.
Прямоугольный треугольник
Радиус окружности, которую вписали в треугольник с прямым углом, представляет собой дробь с числителем в виде суммы катетов за минусом гипотезы и знаменателем, равным числу 2.
Источник: microexcel.ru
В формуле a и b являются катетами, c – гипотенузой треугольника.
Равнобедренный треугольник
Радиус окружности, которая вписана в равнобедренный треугольник, определяют по формуле:
Источник: microexcel.ru
В этом случае a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Расчет радиуса окружности, которая вписана в правильный или равносторонний треугольник, выполняют по формуле:
Источник: microexcel.ru
где a – сторона геометрической фигуры с тремя углами.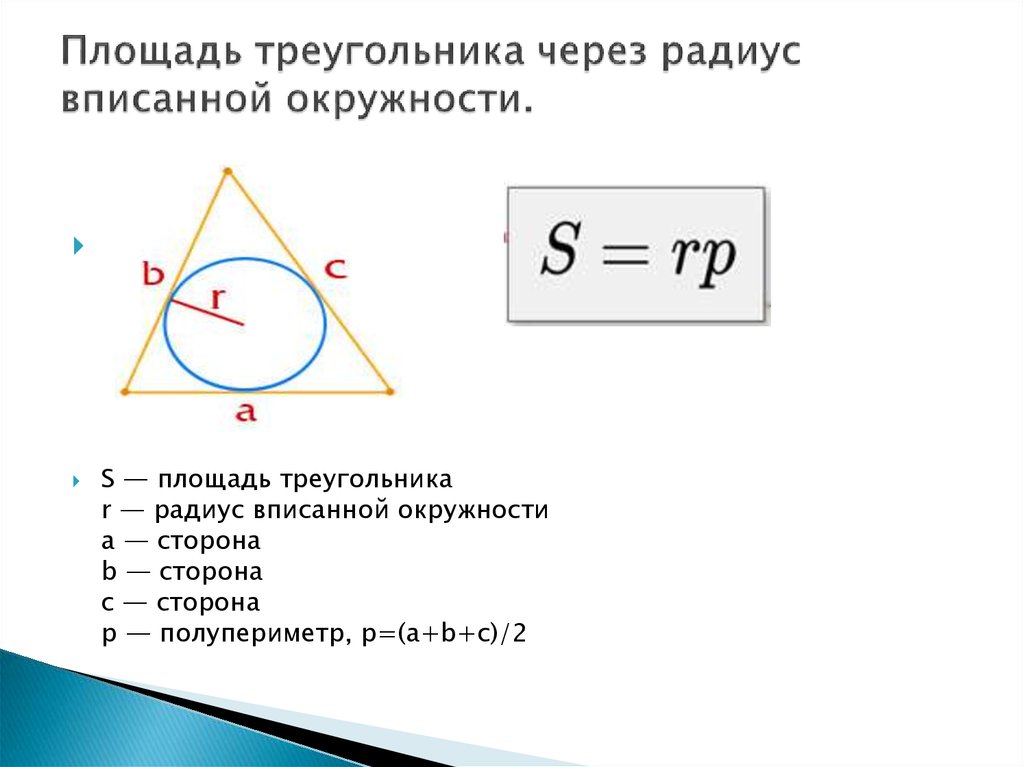
Как найти через высоту или стороны, примеры решения
Задача 1
Имеется геометрическая фигура с тремя углами, стороны которой составляют 5, 7 и 10 см. Требуется определить радиус окружности, которая вписана в этот треугольник.
Решение
В первую очередь необходимо определить, какова площадь треугольника. Для этого можно воспользоваться формулой Герона:
Источник: microexcel.ru
Затем применим формулу для расчета радиуса круга:
Источник: microexcel.ru
Ответ: радиус окружности составляет примерно 1,48 см.
Задача 2
Необходимо рассчитать радиус окружности, которая вписана в равнобедренный треугольник. Боковые стороны геометрической фигуры составляют 16 см, а основание равно 7 см.
Решение
Следует использовать подходящую формулу для расчета радиуса, подставив в нее известные величины:
Источник: microexcel.ru
Ответ: радиус окружности примерно равен 2,8 см.
Насколько полезной была для вас статья?
Рейтинг: 3.50 (Голосов: 2)
Поиск по содержимому
Радиусы описанной и вписанной окружностей в квадрат
Окружность вписанная в квадрат
Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:
- все углы прямые, то есть, равны 90°;
- все стороны, как и углы, равны;
- диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°.
Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:
Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.
Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:
Легко решить и обратную задачу.
Находим из этого уравнения неизвестное значение: .
Окружность описанная около квадрата
Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):
Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:
- угол CDA=90°;
- стороны AD=CD. Признак равнобедренного треугольника;
- угол DAC равен ACD.
Они равны по 45°.
Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:
Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:
Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна , тогда:
Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
Рассмотрим пример
Задача
: радиус окружности вписанной в квадрат равен . Найти радиус окружности описанной около этого квадрата.
Дано
:
- треугольник ОСЕ – равнобедренный и прямоугольный;
- ОЕ=ЕС=;
- ОЕС=90°;
- ЕОС=ОСЕ=45°;
Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.
Как рассчитать радиус маленького круга | Широта и долгота
На изображении выше показан радиус маленького круга.
Для расчета радиуса малого круга необходимы два основных параметра: значение R и значение широты северной или южной широты экватора (α).
Формула для расчета радиуса малого круга:
r = Rcosα
Где:
r = Радиус малого круга или Радиус параллели 9 широты0019 R = радиус Земли
α = значение широты к северу или югу от экватора
Давайте решим пример;
Найдите радиус маленького круга, если значение R равно 6400, а значение широты к северу или югу от экватора равно 22.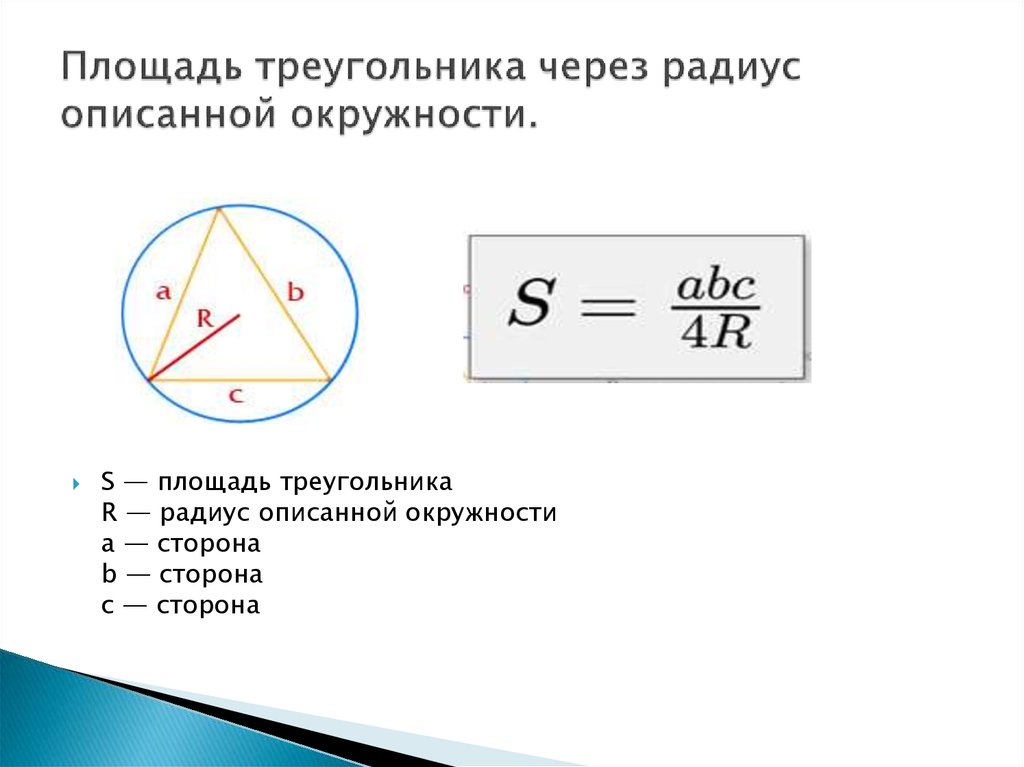
Отсюда следует, что;
R = радиус Земли = 6400
α = значение широты к северу или югу от экватора = 22
r = Rcosα
r = 6400 x cos22°
r = 6400 x 0,927
r = 79030,00002 Следовательно, радиус малого круга равен 5933,97 км.
Расчет значения широты к северу или югу от экватора, когда известны радиус малого круга и значение R.
α = r / Rcos
Где:
α = Значение широты к северу или югу от экватора
R = Радиус Земли
r = Радиус малого круга параллели или Широта
Решим пример;
Найдите значение широты к северу или югу от экватора с радиусом малого круга, равным 20, и значением R, равным 6400.
Отсюда следует, что;
R = Radius of the Earth = 6400
r = Radius of the small circle or Radius of Parallel of Latitude =20
α = r / Rcos
α = 20 / 6400cos
α = 20 / 0,1736
α = 115,207
Следовательно, значение широты к северу или югу от экватора — это 115,207°.
Калькулятор Никзома – Энциклопедия калькулятора способна вычислить радиус маленького круга.
Чтобы получить ответ и вычисления радиуса малого круга с помощью Калькулятор Никзома – Энциклопедия калькулятора. Во-первых, вам нужно получить приложение.
Вы можете получить это приложение любым из следующих способов:
Интернет – https://www.nickzom.org/calculator-plus
Чтобы получить доступ к0007 профессиональная версия через Интернет, вам необходимо зарегистрироваться и подписаться за 1500 NGN за годовой , чтобы иметь полный доступ ко всем функциям.
Вы также можете попробовать демо-версию через https://www.nickzom.org/calculator
Android (платная) – https://play.google.com/store/apps/details?id=org .nickzom.nickzomcalculator
Android (бесплатно) – https://play.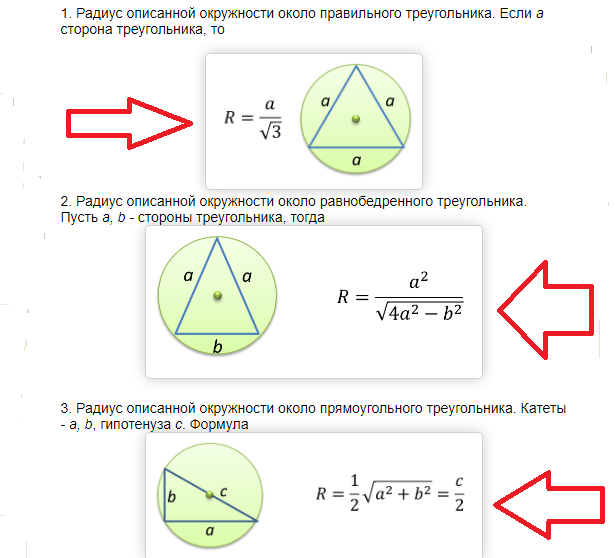
Apple (платно) – https://itunes.apple.com/us/app/nickzom-calculator/id1331162702?mt=8
После того, как вы получили приложение энциклопедии калькулятора, перейдите к Карта калькулятора, затем нажмите Широта и долгота под Математика .
Теперь нажмите Радиус маленького круга под Широта и долгота
На снимке экрана ниже показана страница или действие для ввода ваших значений, чтобы получить ответ для радиуса маленького круга в соответствии с к соответствующим параметрам, которые являются значение R и значение широты северной или южной широты экватора (α).
Теперь введите соответствующие значения для параметров в соответствии с требованиями значение R равно 6400 и значение широты северной или южной широты экватора (α) равно 22 .
Наконец, нажмите «Вычислить».
Опубликовано Ноябрь 21, 2019 Автор Loveth IdokoКатегории МатематикаТеги энциклопедия калькулятора, широта и долгота, математика, калькулятор nickzom, радиус малого круга, значение R, значение широты N или S экватора
Видео-вопрос: нахождение радиуса внутренней окружности, касающейся сторон треугольника, с использованием заданного соотношения и длин сторон треугольника
Длины треугольника равны 12 см, 5 см и 11 см. Найдите радиус внутренней окружности, касающейся сторон, по формуле 𝑟 = площадь (△𝐴𝐵𝐶)/𝑝, где 𝑝 — половина периметра треугольника.
Стенограмма видео
Длина треугольника равна 12
сантиметры, пять сантиметров и 11 сантиметров. Найдите внутренний радиус
окружность, касающаяся сторон по формуле 𝑟, равна площади треугольника
𝐴𝐵𝐶 над 𝑝, где 𝑝 — половина периметра треугольника.
Ну, чтобы мы могли использовать
Формула радиуса круга, нам нужно найти площадь
треугольник. И то, что нам говорят, три стороны
длины нашего треугольника: 12, 5 и 11. Ну, а если у нас три длины сторон
треугольника, то мы можем использовать формулу Герона, чтобы найти площадь. А формула Герона говорит нам, что
площадь равна квадратному корню из 𝑠, умноженному на 𝑠 минус 𝑎, умноженному на
𝑠 минус 𝑏, умноженный на 𝑠 минус 𝑐, где 𝑎, 𝑏 и 𝑐 — длины сторон
наш треугольник. А 𝑠 равно 𝑎 плюс 𝑏 плюс
𝑐 больше двух, потому что это полупериметр нашего треугольника. Ну, на самом деле, это связано с
формула для радиуса у нас есть, потому что нам сказали, что формула для
радиус равен площади треугольника, деленной на 𝑝, где 𝑝 — половина
периметр треугольника. Ну, по сути, это то же самое, что и
𝑠 потому что оба они означают полупериметр или половину периметра треугольника.
Итак, первое, что мы хотим сделать
узнать площадь треугольника. А для этого, во-первых, нам нужно
найдите полупериметр или 𝑝, половину периметра треугольника. Ну, это будет равно 12
плюс пять плюс 11 на два. Итак, это будет равно 14
сантиметры. Так здорово, что мы можем сделать сейчас
подставьте это в формулу Герона. И когда мы это сделаем, мы собираемся
получить площадь равна корню квадратному из 14 умножить на 14 минус 12 умножить
на 14 минус пять умножить на 14 минус 11, что равно корню 756. А если это упростить, то получится шесть
корень 21. И мы сохраним его в сурде
форме, чтобы сохранить точность, и единицами для этого будут сантиметры в квадрате, потому что
это наш район.
Хорошо, отлично. Итак, теперь у нас есть все, что нужно
подставить в формулу для нахождения радиуса. Что мы сделали, так это то, что мы набросали
то, что мы пытаемся найти, потому что мы пытаемся найти радиус
внутренний круг, который касается сторон нашего треугольника.


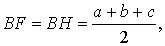

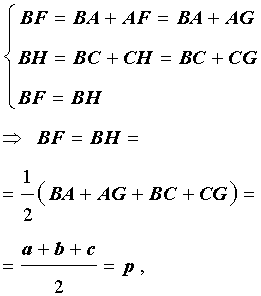
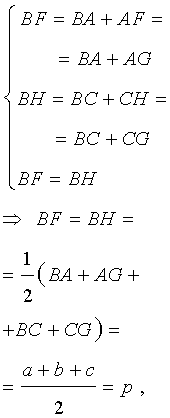
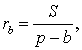
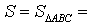

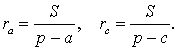
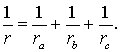
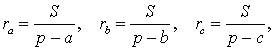
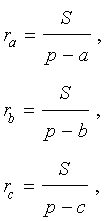
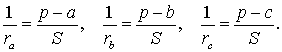
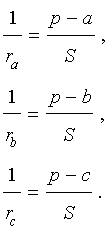
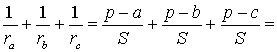
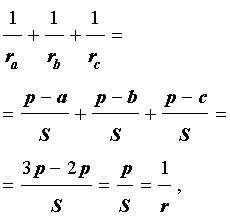
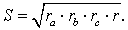
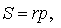
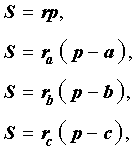
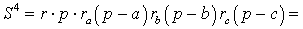
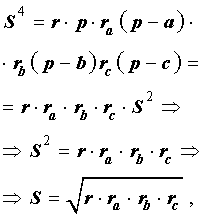
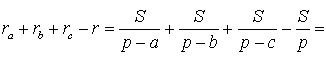
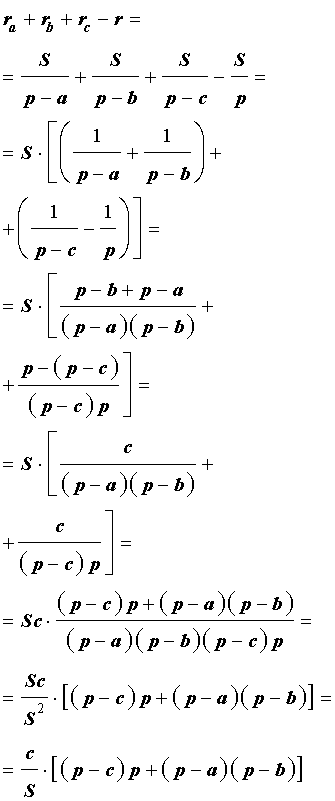


















































 Можно сделать вывод о совпадении этих окружностей.
Можно сделать вывод о совпадении этих окружностей.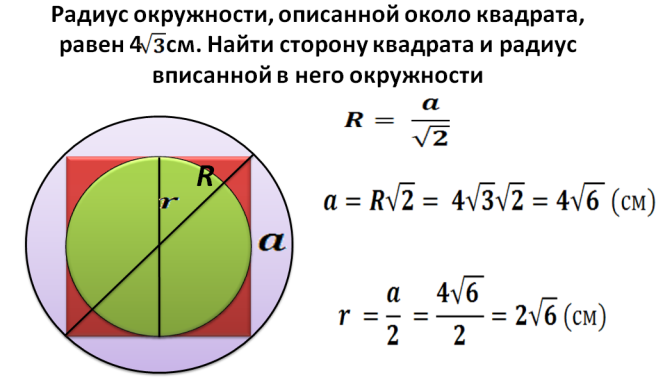 Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей.
Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей. Они равны по 45°.
Они равны по 45°.