Как найти радиус окружности описанной около многоугольника - Исправление недочетов и поиск решений вместе с Examum.ru

В публикации представлена формула, с помощью которой можно найти радиус окружности, описанной около правильного многоугольника, а также приведен пример решения задачи для лучшего понимания представленного материала.

Формула расчета радиуса окружности
Пример задачи

Формула расчета радиуса окружности

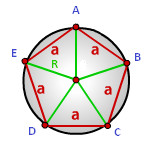
На рисунке изображен правильный шестиугольник с описанной вокруг него окружностью, но формула ниже подходит для любого правильного n-угольника.

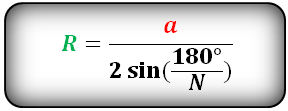
где a – длина стороны.

Примечание: зная радиус описанного круга можно найти сторону равностороннего n-угольника (формула выводится из представленной выше):

Пример задачи

Дан правильный пятиугольник с длиной стороны 8 см. Вычислите радиус описанной около данной фигуры окружности.

Решение:
Применим соответствующую формулу, подставив в нее известное нам значение.

Источник

Радиус описанной окружности правильного многоугольника

a — сторона многоугольника

N — количество сторон многоугольника

Формула радиуса описанной окружности правильного многоугольника, (R):

Калькулятор — вычислить, найти радиус описанной окружности правильного многоугольника

Подробности

Автор: Administrator

Опубликовано: 10 сентября 2011

Обновлено: 13 августа 2021

Источник

Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.

Радиус описанной окружности для произвольного треугольника

Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

$[R = frac{{abc}}{{4S}}]$

$[R = frac{a}{{2sin alpha }} = frac{b}{{2sin beta }} = frac{c}{{2sin gamma }},]$

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

Центр описанной окружности лежит:

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

$[R = frac{c}{2}]$

Окружность, описанная около многоугольника

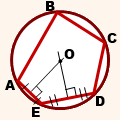
Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

$[R = frac{a}{{2sin frac{{{{180}^o}}}{n}}}]$

где a — длина стороны многоугольника, n — количество его сторон.

Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.

Радиус описанной окружности правильного треугольника

Формула радиуса описанной окружности для правильного треугольника

$[R = frac{a}{{sqrt 3 }}]$

Если без иррациональности в знаменателе —

$[R = frac{{asqrt 3 }}{3}.]$

У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:

Радиус описанной окружности квадрата

Формула радиуса описанной окружности для квадрата

$[R = frac{a}{{sqrt 2 }}]$

Если без иррациональности в знаменателе —

$[R = frac{{asqrt 2 }}{2}.]$

Радиус описанной окружности правильного шестиугольника

Формула радиуса описанной окружности для правильного шестиугольника

Источник

Радиус описанной окружности правильного многоугольника, формула

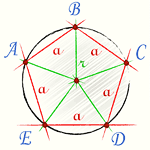
Правильный многоугольник — это многоугольник с равными сторонами и углами. Угол между двумя соседними вершинами правильного n-угольника равен:

[AOB = α = frac{360°}{n}]

Радиус описанной окружности правильного многоугольника

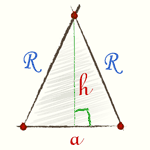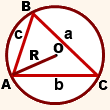
Построим треугольник AOB отдельно. Об этом треугольнике мы знаем: он равнобедренный, и бедра этого треугольника это радиусы описанной окружности правильного многоугольника. Также нам известна длина основания a этого треугольника — которое является стороной исходного правильного многоугольника.

Также известен угол между радиусами R — по формуле (1).
Опустим высоту на основание и рассмотрим получившийся прямоугольный треугольник.
При помощи тригонометрических функций острого угла получим:

[sinBig(frac{360°}{2n}Big) = frac{a}{2R}]

отсюда получим формулу радиуса описанной окружности правильного многоугольника:

[R = frac{a}{2 sin(frac{360°}{2n})}]

(a — сторонa правильного многоугольника; n — число сторон правильного многоугольника; R — радиус описанной окружности правильного многоугольника)

Вычислить, найти радиус описанной окружности правильного многоугольника по формуле (3)

Радиус описанной окружности правильного многоугольника	стр. 251

Источник

Радиус описанной окружности вокруг правильного многоугольника равен отношению его стороны к двум синусам угла, представляющего собой частное 180 градусов и количества сторон. Вывести из этого формулу стороны можно, умножив радиус на знаменатель.
R=a/(2 sin⁡〖(180°)/n〗 )
a=2R sin⁡〖(180°)/n〗

Тогда периметр многоугольника будет равен произведению этого выражения на количество сторон.
P=na=2nR sin⁡〖(180°)/n〗

Радиус вписанной окружности выглядит похожим образом на радиус описанной окружности, поэтому при подстановке выведенной формулы вместо стороны многоугольника, выражение частично упростится.
r=a/(2 tan⁡〖(180°)/n〗 )=r=(2R sin⁡〖(180°)/n〗)/(2 tan⁡〖(180°)/n〗 )=R cos⁡〖(180°)/n〗

Площадь равностороннего многоугольника равна квадрату стороны, умноженному на количество сторон и деленному на четыре тангенса означенного угла, поэтому выразив сторону через радиус, получится n-ное количество квадратов радиуса описанной окружности, умноженное на тангенс известного угла.
S=(na^2)/(4 tan⁡〖(180°)/n〗 )=(n(2R sin⁡〖(180°)/n〗 )^2)/(4 tan⁡〖(180°)/n〗 )=nR^2 tan⁡〖(180°)/n〗

При этом сам внутренний угол многоугольника остается равен произведению разности количества сторон и двух на 180 градусов, деленных на n.
α=(n-2) (180°)/n

Источник