Отрезки и прямые, связанные с окружностью. Теорема о бабочке
Отрезки и прямые, связанные с окружностью
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Конечная часть плоскости, ограниченная окружностью
Отрезок, соединяющий центр окружности с любой точкой окружности
Отрезок, соединяющий две любые точки окружности
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Прямая, пересекающая окружность в двух точках
| Фигура | Рисунок | Определение и свойства |
| Окружность |  |
|
| Круг |  |
|
| Радиус |  |
|
| Хорда |  |
|
| Диаметр |  |
|
| Касательная |  |
|
| Секущая |  |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Радиус
Отрезок, соединяющий центр окружности с любой точкой окружности
Хорда
Отрезок, соединяющий две любые точки окружности
Диаметр
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Касательная
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Секущая
Прямая, пересекающая окружность в двух точках
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  |
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  |
Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  |
У равных дуг равны и хорды. |
| Параллельные хорды |  |
Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины
Большая из двух хорд расположена ближе к центру окружности.
Равные дуги
У равных дуг равны и хорды.
Параллельные хорды
Дуги, заключённые между параллельными хордами, равны.
Теоремы о длинах хорд, касательных и секущих
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды |  |
|
| Касательные, проведённые к окружности из одной точки |  |
|
| Касательная и секущая, проведённые к окружности из одной точки |  |
|
| Секущие, проведённые из одной точки вне круга |  |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
| Пересекающиеся хорды |
 |
| Касательные, проведённые к окружности из одной точки |
 |
| Касательная и секущая, проведённые к окружности из одной точки |
 |
| Секущие, проведённые из одной точки вне круга |
 |
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Касательные, проведённые к окружности из одной точки
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга
Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
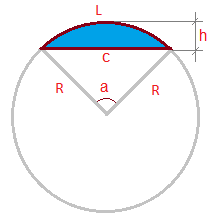
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Все основные формулы для определения длины радиуса окружности
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2 R
Формула для определения длины радиуса, если известна площадь круга :
Калькулятор для расчета длины радиуса через площадь
Формула для определения длины радиуса, если известна длина окружности :
Калькулятор для расчета длины радиуса через длину окружности
R — радиус окружности (круга)
h — высота сегмента
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
http://planetcalc.ru/1421/
http://www-formula.ru/radius-if-known-area
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Как найти радиус по хорде
Хорда — это отрезок, соединяющий две точки окружности. Пусть длина хорды известна. Тогда, если также известен угол между радиусами, проведенными в концы хорды, то можно найти и радиус окружности.
Вам понадобится
- Транспортир, линейка.
Инструкция
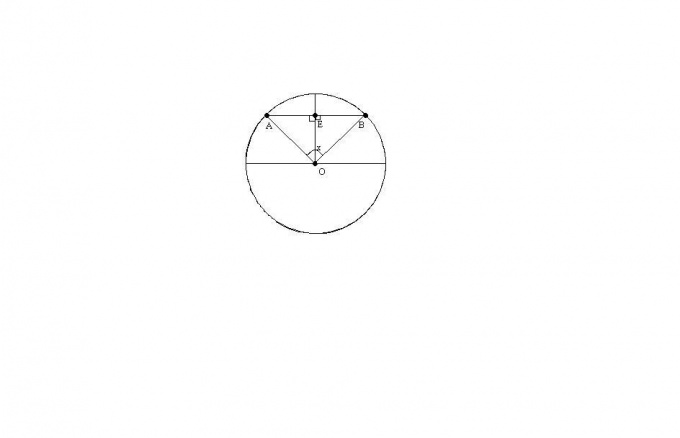
Пусть известны длина хорды AB и угол AOB между радиусами, проведенными в концы хорды. Найдем по этим данным радиус окружности с центром в точке O.
Треугольник AOB — равнобедренный, так как OA = OB = R. По свойству равнобедренного треугольника высота OE одновременно является его медианой и биссектрисой угла AOB. Обозначим угол AOB за х.
Треугольник AEO — прямоугольный с прямым углом AEO. Так как высота ОЕ также является биссектрисой угла AOB, то угол AOE = x/2. Тогда из прямоугольного треугольника AOE имеем: OA = R = (AB/2)/sin(x/2).
|
Встретил забавную задачу и приглашаю многоуважаемую публику ей поразвлечься… ) Есть окружность. Внутри окружности проведена хорда a, от одного из концов этой хорды проведен внутри окружности под прямым углом отрезок b так, что он не пересекает и не касается окружности. От второго конца отрезка b опять же, под прямым углом, проведен отрезок с, который вторым концом касается окружности. Длина всех отрезков больше нуля. Отрезки a и с лежат в разных полуплоскостях относительно прямой, проходящей через отрезок b. Я не знаю, вроде все по условиям, все как на картинке, честное слово! Мы знаем длины a, b и c. Нужно найти радиус окружности. Можно воспользоваться свойствами хорды, готовыми уравнениями. Точка пересечения двух хорд делит обе хорды в одинаковом соотношении. Используем эту формулу для нахождения отрезка d (cм. рисунок). Когда хорды перпендикулярны то радиус окружности находится по второй формуле. автор вопроса выбрал этот ответ лучшим Тут вспомнил, как мне один раз на практике нужно было найти радиус окружности и были три точки.. Сделано это было простым графическим методом без всяких заумностей.. Просто известно, что радиус в каждой точке окружности перпендикулярен касательной к окружности (которая есть суть производной, но это так, к слову).. Далее, известно, что хорда всегда идёт параллельно касательной (собственно касательная — это хорда сдвинутая на край окружности и касающаяся её в одной точке).. Вот и всё, что нужно.. Без матриц, определителей, систем уравнений, хитроумных формул и построений.. Итак, вот рисунок.. Т. е., мы просто достроили ещё одну хорду (красным цветом), затем каждую хорду поделили пополам и из середины каждой хорды провели линии, перпендикулярные хорде.. Точка пересечения двух линий, перпендикулярных хордам и есть центр окружности.. Теперь из цента мы ставим ногу циркуля и рисуем окружность (можно использовать карандаш на нитке (как пришлось использовать на практике).. Также для построения перпендикуляров использовалась нитка и древний способ построения перпендикуляров.. Деление напополам: сложение отмеренной нитки вдвое.. Всё делается на коленке.. И даже можно использовать на местности для построения окружностей в масштабах сотен метров и более.. Т.е. мы нашли не только радиус, но даже центр окружности и при желании можем с помощью циркуля (или карандаша на нитке) построить искомую окружность.. Именно так на практике мне один раз пришлось искать окружность, причём нужно было знать не только радиус, но расположение центра.. Этот метод наиболее прост, универсален и с помощью его можно искать все параметры окружности.. Если нужно найти радиус с наперёд заданной точностью, то можно использовать метод в моём предыдущем ответе, решение системы из трёх квадратных уравнений, которые описывают нахождение трёх точек, можно решать их не обязательно аналитически, что немного трудоёмко (но не сложно), а используя тот же Маткад.. Кроме того этот аналитический метод может помочь определить не только радиус окружности, но и координаты центра с любой заданной точностью, т.е. все параметры окружности.. Кстати, посткриптум, этот графический метод пришлось придумывать на ходу, поскольку нужно было срочно найти ответ, искать что-то в литературе как найти окружность просто не было времени.. Конечно хорошо знать определитель, которым задаётся дуга окружности через 3 точки.. Как это написал Гр. Роджер.. Можно сделать хитроумные геометрические построения, как сделал родиоил2.. Можно использовать свойства дуги, как попытался это сделать мсб.. Но вот, положим вам на практике нужно быстро определить, тогда нужно искать свойства дуг, определителей?.. Или пыхтеть с построениями? Которые могут быть не очень точны из-за несовершенства инструментария.. Как же поступить? Да как на войне: быстро и эффективно, используя смекалку и минимум средств.. Воспользуемся простыми формулами, которые известны из школы.. И элементами аналитической геометрии (опять это практически школа).. Известно, что уравнение окружности: (x-xo)^2+(y-yo)^2=R^2 где xo, y0, R — соответственно координаты центра и радиус окружности.. Установим первую точку А так, чтобы она находилась в начале координат А(0,0), тогда следующая точка В имеет координаты (0,а), следующая точка С (b, c+a).. Теперь напишем три уравнения одной и той же окружности для трёх точек: (xo)^2+(yo)^2=R^2 (xo)^2+(а-yo)^2=R^2 (b-xo)^2+(с+а-yo)^2=R^2 Получилась система из трёх квадратных уравнений с тремя неизвестными: xo, y0, R.. Значит эта система вполне решается стандартным образом.. Например приравниваем первое и второе уравнение: (xo)^2+(yo)^2=(xo)^2+(а-yo)^2 Тогда всё приводится к уравнению: (yo)^2-(а-yo)^2=0 Упрощаем его и получаем простое линейное уравнение: -2ay0-(а)^2=0 y0=-(а)^2/2a=-a/2 Из него находим первую координату центра.. Затем эту координату подставляем в первое уравнение (которое попроще): (xo)^2+(a/2)^2=R^2 x0=+(-)sqrt(R^2-(a/2)^2) Теперь координаты центра подставляем опять в третье уравнение: (b-R^2-(a/2)^2)^2+(с+а+a/2)^2=R^2 Далее всё приводим, раскрывая скобки, получая уравнение 4-й степени.. Не в каждой школе дают решение уравнения 4-й степени, но это не сложно используя метод Феррари или метод разложения на множетели.. Грустный Роджер 2 года назад Это трёхходовка на аналитическую геометрию. Я расскажу, как она решается, но вычисления вы уж проведите сами… Будем считать, что длины всех трёх отрезков нам известны, и будем для простоты считать, что начало координат находится в точке сопряжения отрезков a, b. Тогда нижний конец отрезка а находится в точке (0, -А) (пусть заглавная буква — это длина соответствующего отрезка), а верхний конец отрезка с находится в точке (В, С). И тогда уравнение окружности, проходящей через три точки с известными координатами, пишется фактически «в одно действие» — через определитель, составленный из координат трёх точек, через которые она проходит: По счастью, при сделанном выше выборе осей координат одна строка определителя получается почти нулевой, и тогда он элементарно превращается в определитель третьего порядка (если знать, что такое минор): Тут, если совсем формально, перед определителем 3 порядка должен стоять минус, но поскольу он равен нулю, то фиг с ним, с минусом… Ну так вот. «Каноническое» уравнение окружности в декартовой системе координат выглядит так: x² + y² + Mx + Ny + K = 0. Если раскрыть определитель, то приравниванием коэффициентов при соответствующих степенях х, у враз получаются выражения для M, N и К. Ну а как только эти величины известны, радиус вычисляется как корень из (M² + N² — 4C). rodleoil2 2 года назад Предлагаю графическое решение Оно поможет найти и математическое решение Чертим линии а,б,с, соблюдая размеры и углы. Чертим одинаковые окружности, чтобы они попарно (одинакового размера рядом) пересекались. на данном чертеже все окружности одинаковые (размеры позволяют). Оранжевые окружности. Проводим линии через пересечения окружностей. Зеленые тонкие линии. Расстояния от точек соприкосновения заданных отрезков «а», «б», а также концов отрезков «а» и «с» и тонких зеленых линий будет радиусом Толстые зеленые линии. Также, легко заметить, что мы проводили тонкие зеленые линии — это серединные перпендикуляры к хордам. При необходимости, математическое решение можно получить работая с размерами отрезков, треугольниками, углами… Но на практике, на чертежах, хватает и графического решения. Грустный Роджер 2 года назад (Продолжение банкета…) Ответ msb натолкнул на забавную мысль: если нужно решить задачу графически, чисто циркулем и линейкой, то хорды b, c вообще на фиг не нужны, потому что есть окружность (это, заметьте, по условию задачки!) и есть хорда в ней. Всё, sapienti sat. На окружности строится ещё одна хорда, лежащая точно напротив хорды а, это делается циркулем и линейкой (проводятся два перпендикуляра к концам отрезка, фигня вопрос…), это нам даёт прямоугольник, вписанный в окружность. Собсно, всё, радиус отсюда определяется на раз. Но и это ещё не конец! Можно не строить этот прямоугольник. Можно построить два перпендикуляра — один к середине хорды a, второй — к середине отрезка, образованного лежащими на окружности концами хорд b, c. Точка их пересечения даст центр окружности. Никольский 2 года назад Фигура АВСD — описанная равнобедренная трапеция (см. рисунок), где а — верхнее основание трапеции, f — нижнее основание трапеции, k — боковая сторона трапеции, m — диагональ трапеции. k и m вычисляются из прямоугольных треугольников, f=2с + а Р — полупериметр треугольника АСD. Р = (m + k + f)/2 Есть формула, по которой вычисляется радиус окружности описанной равнобедренной трапеции: R = (kmf)/(4(sqrt(P(P-k)(P-m)(P-f))) Выражая k, m, f через а, в, с, получим (даже не буду пытаться) конечную формулу. Если знать конкретные числовые значения а, в, с, то найти R можно с помощью калькулятора. Геометрические задачи решаются графически. Здесь много лишних данных. Достаточно продлить отрезок b до пересечения с окружностью и соединить линией эту точку пересечения с точкой пересечения отрезка a c окружностью. Это будет диаметр окружности, который только остается разделить пополам с помощью циркуля и линейки и измерить. Знаете ответ? |
Сегмент круга
Данный калькулятор считает параметры сегмента круга, а именно:
Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:
1) сегмент круга решается с помощью радиуса (R) и угла (A).
2) сегмент круга находим с помощью высоты и длины хорды.
Однако, как справедливо заметил наш пользователь:«на практике hourто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента, вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу: