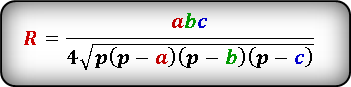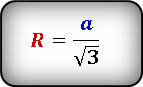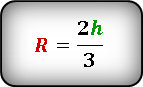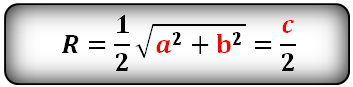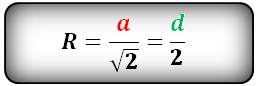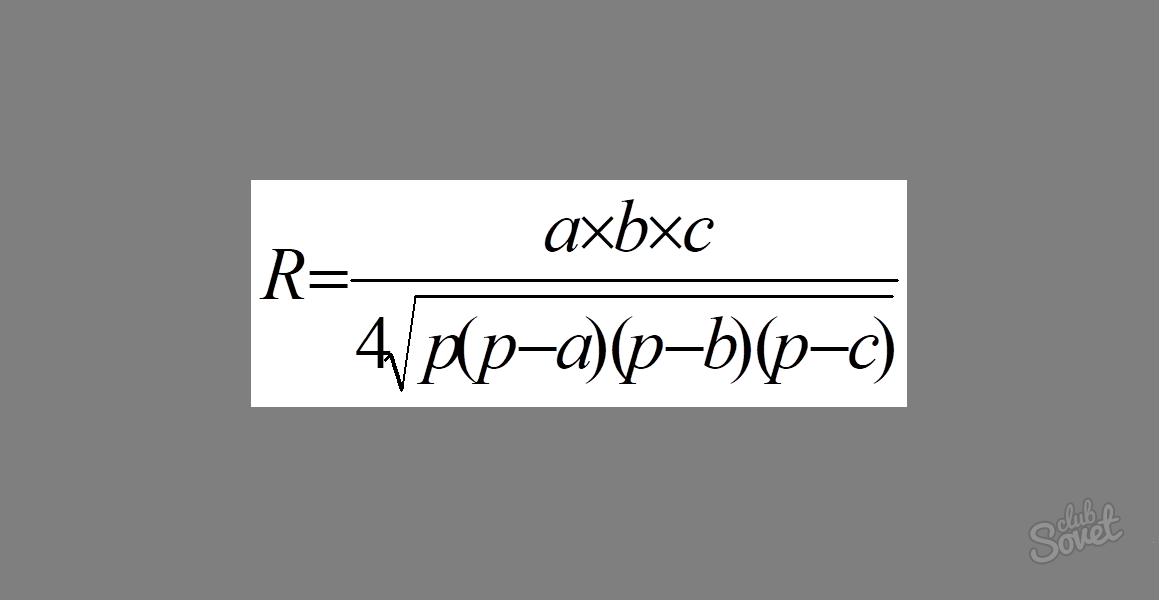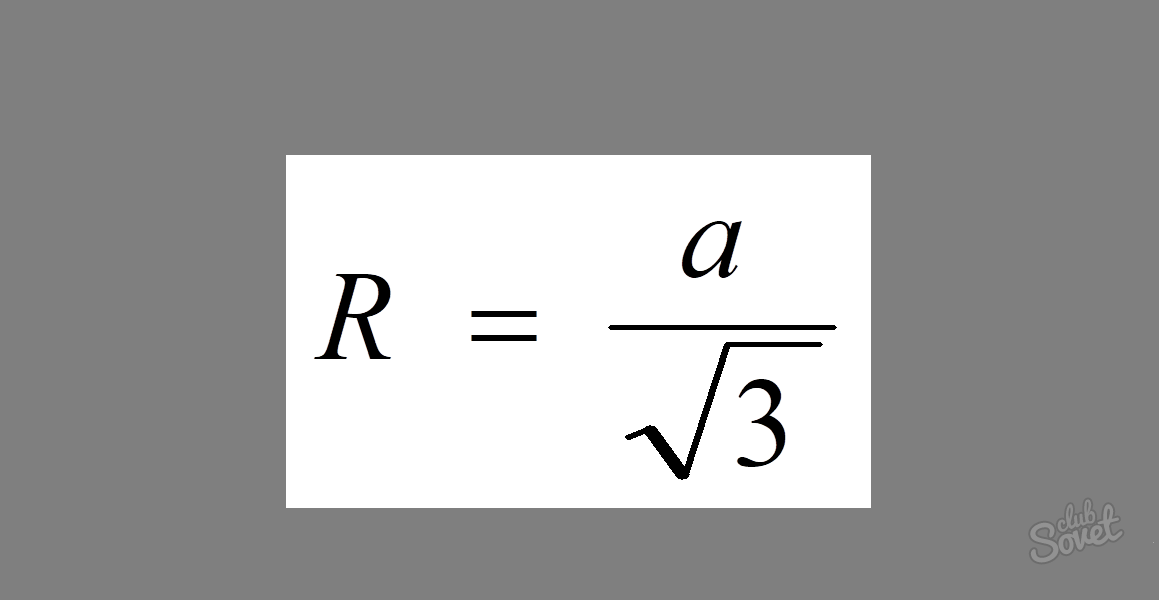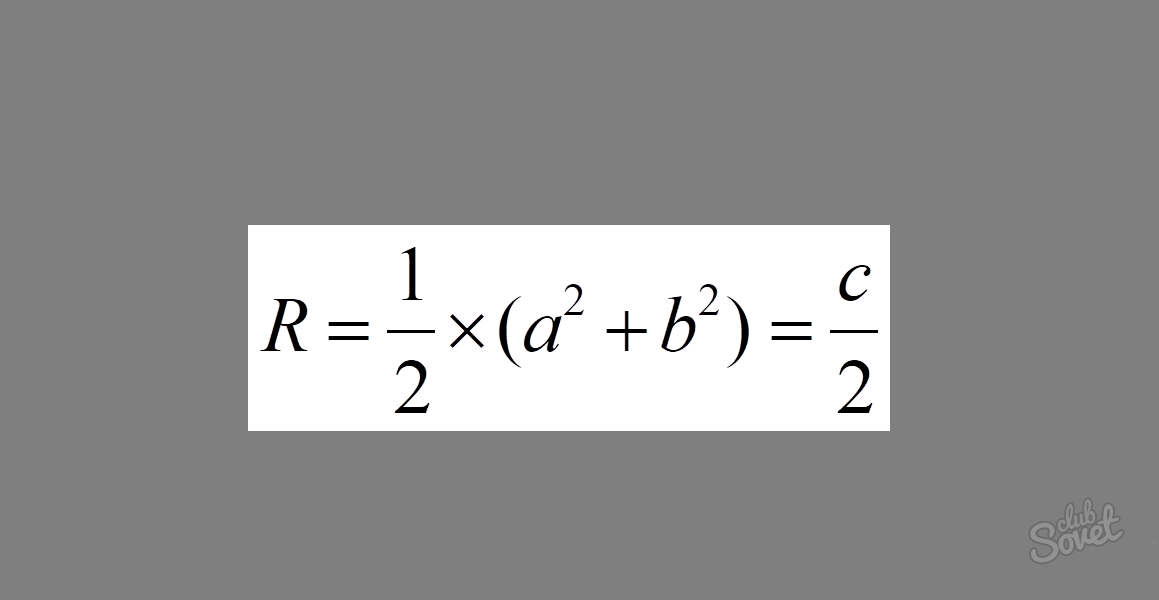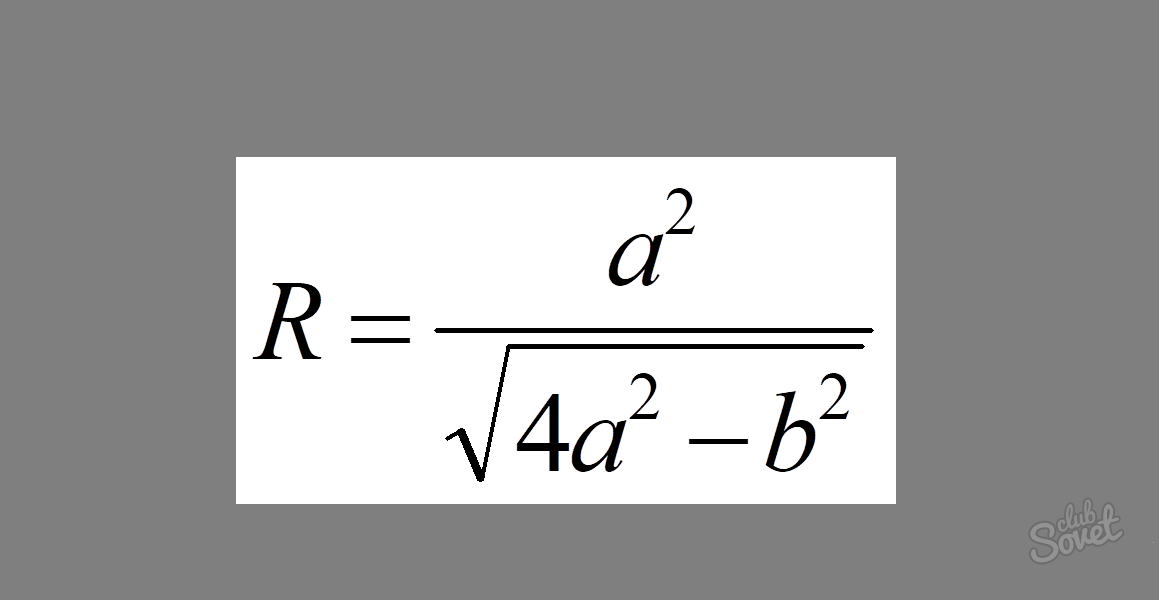Радиус описанной окружности прямоугольного треугольника
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a , b — катеты прямоугольного треугольника
c — гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
Калькулятор — вычислить, найти радиус описанной окружности прямоугольного треугольника
Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
Радиус описанной окружности около прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.
На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:
( small R=frac<large c> <large 2 sin C>)
где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:
( small R=frac<large c><large 2 sin 90°>=frac<large c><large 2>, )
| ( small R=frac<large c><large 2>. ) | (1) |
Пример 1. Известна гипотенуза ( small с=frac<9> <2>) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).
Подставим значение ( small c=frac<9> <2>) в (1):
Ответ: 
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).
Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:
| ( small c=sqrt. ) | (2) |
Подставляя (2) в (1), получим:
| ( small R=frac<large sqrt><large 2>. ) | (3) |
Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):
Ответ: 
3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):
 |
(4) |
4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.
Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:
( small angle A+angle B=90°. )
| ( small angle A=90°-angle B. ) | (5) |
Подставляя (5) в (4), получим:
( small R=frac<large a><large 2 sin A>=frac<large a><large 2 sin(90°-B)>) ( small =frac<large a> <large 2 cos B>)
| ( small R=frac<large a><large 2 cos B>. ) | (6) |
Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):
Ответ: 
http://matworld.ru/geometry/radius-opisannoj-okruzhnosti-pryamougolnogo-treugolnika.php
Радиус описанной окружности около прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
- Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
- Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
- Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.
На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:
где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:
то есть
Пример 1. Известна гипотенуза ( small с=frac{9}{2} ) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).
Подставим значение ( small c=frac{9}{2} ) в (1):
Ответ:
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).
Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:
Подставляя (2) в (1), получим:
или
Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):
Ответ:
3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):
4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.
Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:
Откуда:
Подставляя (5) в (4), получим:
или
Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):
Ответ:
Смотрите также:
- Радиус описанной окружности около треугольника онлайн
- Радиус описанной окружности около равностороннего треугольника онлайн
- Радиус описанной окружности около равнобедренного треугольника онлайн
, 
, 
— стороны треугольника
— полупериметр
2.png)
— центр окружности
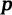
Формула радиуса описанной окружности треугольника ( R ) :
— сторона треугольника
— высота
— радиус описанной окружности
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Формула радиуса описанной окружности равнобедренного треугольника(R):
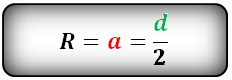
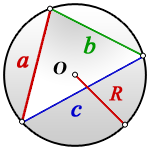
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a, b — катеты прямоугольного треугольника
c — гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
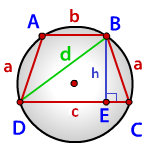
d — диагональ
p — полупериметр треугольника DBC
p = (a+d+c)/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
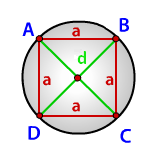
Радиус описанной окружности квадрата равен половине его диагонали
a — сторона квадрата
d — диагональ
Формула радиуса описанной окружности квадрата (R):
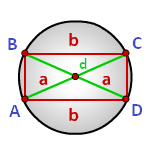
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b — стороны прямоугольника
d — диагональ
Формула радиуса описанной окружности прямоугольника (R):
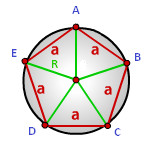
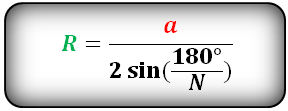
a — сторона многоугольника
N — количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
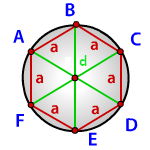
a — сторона шестиугольника
d — диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Вокруг любого треугольника можно описать окружность. Центр описанной вокруг треугольника окружности может лежать как во внутреннем пространстве, так и на стороне треугольника или даже вне его. Для того чтобы найти радиус окружности, описанной вокруг произвольного треугольника, необходимо произведение его сторон разделить на четыре квадратных корня из полупериметра, умноженного на его разность с каждой стороной.
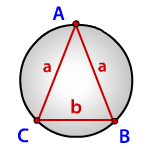
Равнобедренный треугольник имеет стороны a, a, b, подставив которые в вышеприведенную формулу, можно значительно ее упростить и привести к следующему виду:
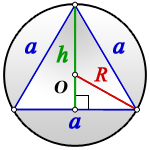
В прямоугольном треугольнике центр описанной окружности лежит в середине гипотенузы, разделяя ее на две части, каждая из которых соединяется с вершинами треугольника, следовательно, является радиусом. Таким образом, чтобы найти радиус окружности, описанной вокруг прямоугольного треугольника, необходимо гипотенузу разделить на два:
Или этот же радиус можно найти, подставив вместо гипотенузы катеты по теореме Пифагора:
Как найти радиус окружности, описанной около треугольника
Очень часто при решении геометрических задач приходится совершать действия со вспомогательными фигурами. Например, находить радиус вписанной или описанной окружности и т.д. Данная статья покажет, как находить радиус окружности, описанной около треугольника. Или, иными словами, радиус окружности, в которую вписан треугольник.
1
Как найти радиус окружности, описанной около треугольника – общая формула
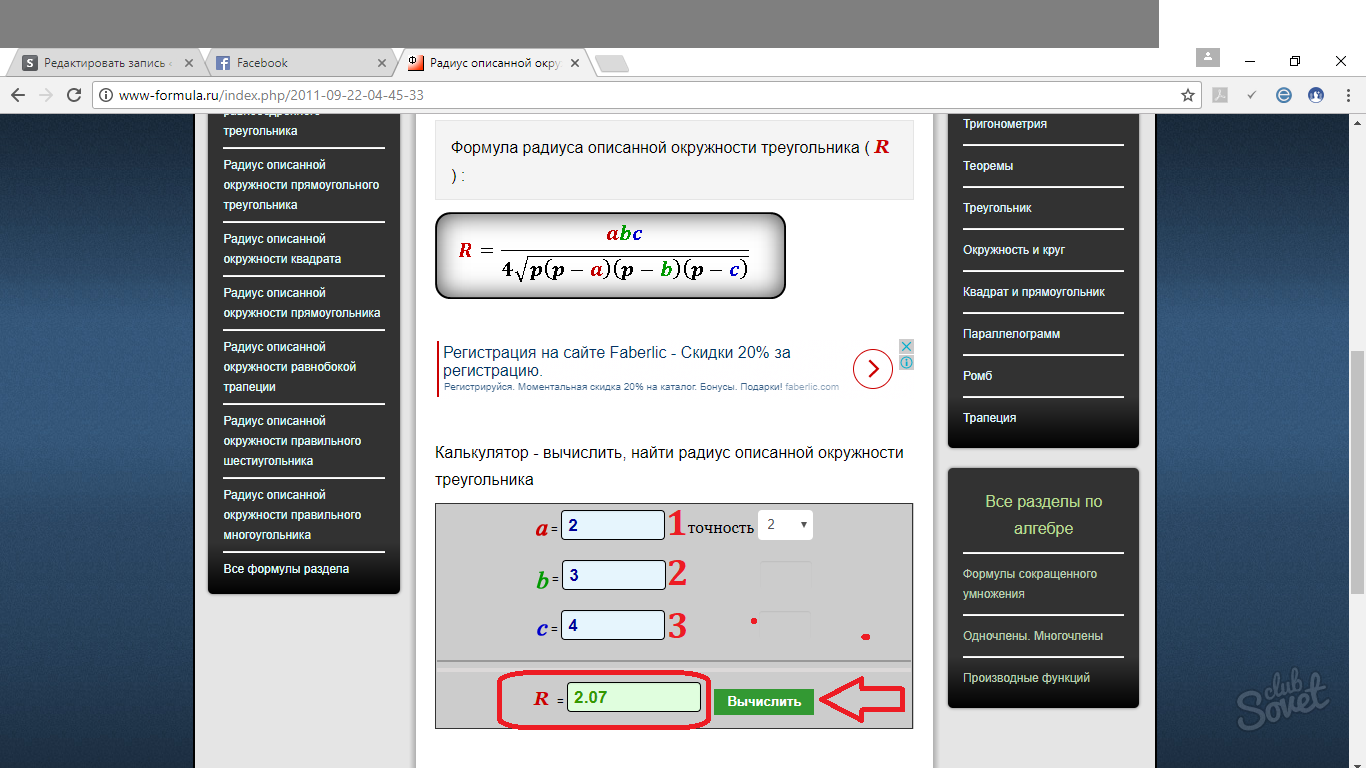
Общая формула выглядит следующим образом: R = abc/4√p(p – a)(p – b)(p – c), где R – радиус описанной окружности, p – периметр треугольника поделенный на 2 (полупериметр). a, b, c – стороны треугольника.
Пример:
Найти радиус описанной окружности треугольника, если a = 3, b = 6, c = 7.
Таким образом, исходя из вышеприведенной формулы, вычисляем полупериметр:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Подставляем значения в формулу и получаем:
R = 3 × 6 × 7/4√8(8 – 3)(8 – 6)(8 – 7) = 126/4√(8 × 5 × 2 × 1) = 126/4√80 = 126/16√5.
Ответ: R = 126/16√5
2
Как найти радиус окружности, описанной около равностороннего треугольника
Для нахождения радиуса окружности, описанной около равностороннего треугольника, существует довольно простая формула: R = a/√3, где a – величина его стороны.
Пример: Сторона равностороннего треугольника равна 5. Найти радиус описанной окружности.
Решение:
Так как у равностороннего треугольника все стороны равны, для решения задачи нужно всего лишь вписать ее значение в формулу. Получим: R = 5/√3.
Ответ: R = 5/√3.
3
Как найти радиус окружности, описанной около прямоугольного треугольника
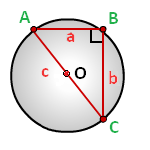
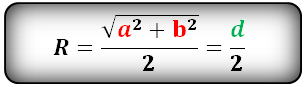
Формула выглядит следующим образом: R = 1/2 × √(a² + b²) = c/2, где a и b – катеты и c – гипотенуза. Если сложить квадраты катетов в прямоугольном треугольнике, то получим квадрат гипотенузы. Как видно из формулы, данное выражение находится под корнем. Вычислив корень из квадрата гипотенузы, мы получим саму длину. Умножение получившегося выражения на 1/2 в итоге приводит нас к выражению 1/2 × c = c/2.
Пример: Вычислить радиус описанной окружности, если катеты треугольника равны 3 и 4. Подставим значения в формулу. Получим: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.
В данном выражение 5 – длина гипотенузы.
Ответ: R = 2.5.
4
Как найти радиус окружности, описанной около равнобедренного треугольника
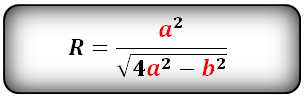
Формула выглядит следующим образом: R = a²/√(4a² – b²), где a – длина бедра треугольника и b – длина основания.
Пример: Вычислить радиус окружности, если его бедро = 7, а основание = 8.
Решение: Подставляем в формулу данные значения и получаем: R = 7²/√(4 × 7² – 8²).
R = 49/√(196 – 64) = 49/√132. Ответ можно записать прямо так.
Ответ: R = 49/√132
5
Онлайн ресурсы для вычисления радиуса окружности
Можно очень легко запутаться во всех этих формулах. Поэтому при необходимости можно воспользоваться онлайн калькуляторами, которые помогут вам в решении задач на нахождение радиуса. Принцип работы таких мини-программ очень прост. Подставляете значение стороны в соответствующее поле и получаете готовый ответ. Можно выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т.д.
Список:
http://www-formula.ru/index.php/2011-09-22-04-45-33
http://www-formula.ru/index.php/2011-09-22-04-51-34
http://www-formula.ru/index.php/2011-09-22-04-52-08
http://www-formula.ru/index.php/2011-09-22-04-52-48
