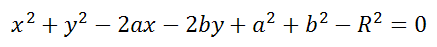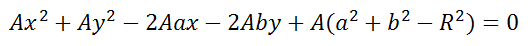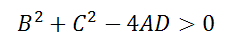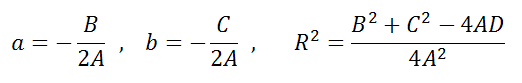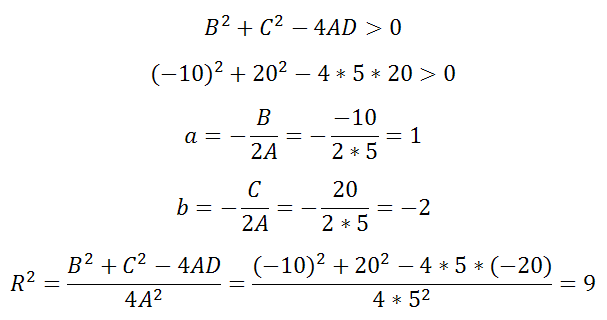Как найти радиус окружности зная координаты точек - Исправление недочетов и поиск решений вместе с Examum.ru

Найти центр и радиус окружности

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

$[3){x^2} + {(y + 3)^2} = 9;]$

$[4){(x - 6)^2} + {y^2} = 5;]$

$[5){x^2} + {y^2} = 11.]$

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

$[3){x^2} + {(y + 3)^2} = 9;]$

Центр окружности — (0;-3), радиус R=3.

$[4){(x - 6)^2} + {y^2} = 5;]$

Центр — в точке (6;0), радиус R=√5.

$[5){x^2} + {y^2} = 11.]$

Чтобы найти центр и радиус окружности, заданной уравнением вида

$[{x^2} + {y^2} - 2ax - 2by + c = 0,]$

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

$[({x^2} - 2ax) + ({y^2} - 2by) + c = 0,]$

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

$[({x^2} - 2ax + {a^2}) - {a^2} + ({y^2} - 2by + {b^2}) - {b^2} + c = 0.]$

$[{(x - a)^2} + {(y - b)^2} + c - {a^2} - {b^2} = 0,]$

$[{(x - a)^2} + {(y - b)^2} = {a^2} + {b^2} - c.]$

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

$[R = sqrt {{a^2} + {b^2} - c} .]$

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Найти координаты центра и радиус окружности:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0;]$

$[2){x^2} + {y^2} - 5x + 4 = 0;]$

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0.]$

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0]$

$[({x^2} + 10x) + ({y^2} - 6y) - 15 = 0]$

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Как найти радиус и центр окружности

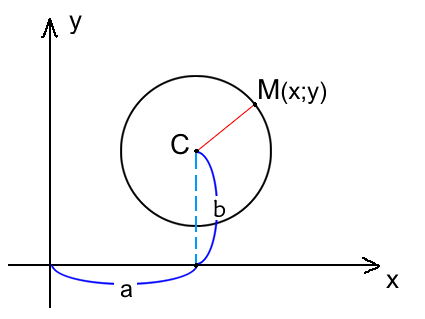
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида:

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

3433

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

(x — l) 2 + (y + 3) 2 = 25

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

x 2 + у 2 = R 2 . (3)

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

x 2 + у 2 = 49.

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

(х + 3) 2 + (у —5) 2 =100.

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

x 2 + у 2 + 4х — 2y — 4 = 0

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

x 2 + 4х + 4— 4 + у 2 — 2у +1—1—4 = 0

(х + 2) 2 + (у — 1) 2 = 9.

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

(x +1) 2 + (y +1) 2 = 144 /₂₅

Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Источник

Если окружность задана уравнением вида

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

найти центр (a;b) и радиус R такой окружности несложно.

Примеры.

Определить по уравнению окружности координаты её центра и радиуса:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

$[3){x^2} + {(y + 3)^2} = 9;]$

$[4){(x - 6)^2} + {y^2} = 5;]$

$[5){x^2} + {y^2} = 11.]$

Решение:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

a=3, b=7, R²=4.

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

$[3){x^2} + {(y + 3)^2} = 9;]$

a=0, b=-3, R²=9.

Центр окружности — (0;-3), радиус R=3.

$[4){(x - 6)^2} + {y^2} = 5;]$

a=6, b=0, R²=5.

Центр — в точке (6;0), радиус R=√5.

$[5){x^2} + {y^2} = 11.]$

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

$[{x^2} + {y^2} - 2ax - 2by + c = 0,]$

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

$[({x^2} - 2ax) + ({y^2} - 2by) + c = 0,]$

$[({x^2} - 2ax + {a^2}) - {a^2} + ({y^2} - 2by + {b^2}) - {b^2} + c = 0.]$

Отсюда

$[{(x - a)^2} + {(y - b)^2} + c - {a^2} - {b^2} = 0,]$

$[{(x - a)^2} + {(y - b)^2} = {a^2} + {b^2} - c.]$

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

$[R = sqrt {{a^2} + {b^2} - c} .]$

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Примеры.

Найти координаты центра и радиус окружности:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0;]$

$[2){x^2} + {y^2} - 5x + 4 = 0;]$

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0.]$

Решение:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0]$

Группируем слагаемые

$[({x^2} + 10x) + ({y^2} - 6y) - 15 = 0]$

$[{x^2} + 10x = ({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2}.]$

Аналогично

$[{y^2} - 6y = ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2}.]$

Таким образом,

$[({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2} + ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2} - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} - 25 - 9 - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} = 49]$

Центром этой окружности является точка (-5;3), радиус R=7.

$[2){x^2} + {y^2} - 5x + 4 = 0]$

$[({x^2} - 5x) + {y^2} + 4 = 0]$

$[({x^2} - 2 cdot x cdot 2,5 + {2,5^2}) - {2,5^2} + {y^2} + 4 = 0]$

$[{(x - 2,5)^2} + {y^2} + 4 - 6,25 = 0]$

$[{(x - 2,5)^2} + {y^2} = 2,25]$

Центр окружности — точка (2,5;0), радиус R=1,5.

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0]$

Разделим обе части уравнения на 3:

$[{x^2} + {y^2} - frac{4}{3}x - 3y + frac{4}{3} = 0]$

Далее — аналогично

$[({x^2} - frac{4}{3}x) + ({y^2} - 3y) + frac{4}{3} = 0]$

$[({x^2} - 2 cdot x cdot frac{2}{3} + {(frac{2}{3})^2}) - {(frac{2}{3})^2} + ({y^2} - 2 cdot y cdot frac{3}{2} + {(frac{3}{2})^2}) - ]$

$[ - {(frac{3}{2})^2} + frac{4}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} - frac{{{4^{backslash 4}}}}{9} - frac{{{9^{backslash 9}}}}{4} + frac{{{4^{backslash 12}}}}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} = frac{{49}}{{36}}]$

Центр этой окружности лежит в точке

$[(frac{2}{3};frac{3}{2}),R = frac{7}{6}.]$

Источник

Как найти радиус и центр окружности

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x² и y² были равны в уравнение вида:

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax²+Bx+Ay²+Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x²-10x+5y²+20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x²+4xy+y²=1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x²+9y²=36 не представляет окружность, так как в нём коэффициенты при x² и y² не равны.

8041

Источник

Уравнение окружности

Решение уравнений

Окружность — геометрическое место расположения множества точек, каждая из которых равноудалена от центра окружности. Отрезок, соединяющий любую точку окружности с ее центром, называется радиусом окружности. Величина радиуса равняется половине диаметра — отрезку, который соединяет две точки окружности, проходя через точку ее центра.

Если в координатную плоскость поместить окружность с радиусом R и центром в точке А, а координаты центра обозначим (а;b), координаты любой точки окружности (х;у), то уравнение окружности будет иметь вид: (х — а)² + (у — b)² = R².

Уравнением окружности называется уравнение, в котором радиус окружности, возведенный в квадрат, равняется сумме квадратов разностей между координатами любой точки окружности и координатами ее центра.

Если центр окружности лежит в точке начала координат, квадрат радиуса окружности равняется сумме квадратов координат любой точки окружности. Уравнение будет иметь вид: х² + у² = R².

Зная координаты точки центра и любой точки окружности можно вычислить длину радиуса, что позволит при необходимости рассчитать длину окружности и площадь круга — плоскости, расположенной внутри окружности.
l = 2π • r;
S = 2π • r²,
где l — длина окружности; r — радиус окружности; S — площадь круга; Пи — 3,14.

Воспользовавшись онлайн калькулятором вы сможете быстро рассчитать уравнение окружности, найти радиус окружности. Для этого потребуется лишь ввести заданные координаты точек.

Источник

Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.

Уравнение окружности

r² = (x — h)² + (y — k)²

где,

h,k — координаты центра Окружности
x,y — координаты точки окружности
r — радиус

Пример

Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)

Решение :

Шаг:1

Подставляем координаты точек в формулу

(2 — h)² + (2 — k)² = r²
(2 — h)² + (4 — k)² = r²
(5 — h)² + (5 — k)² = r²

Шаг :2

Найдем значение k упрощая 1 и 2 уравнения

(2 — h)² + (2 — k)² = (2 — h)² + (4 — k)²
4 — 4h + h²+ 4 — 4k + k² = 4 — 4h + h²+16 — 8k + k²
8 — 4k = 20 — 8k
k=3

Шаг :3

Найдем значение h упрощая уравнения 2 и 3

(2 — h)² + (2 — k)² = (5 — h)² + (5 — k)²
4 — 4h + h²+ 4 — 4k + k² = 25 — 10h + h²+ 25 — 10k + k²
8 — 4k — 4h = 50 — 10h — 10k
6k + 6h = 42

Подставив значение k=3 в уравнение

6h = 24
h=4

Получаем координаты точки центра (h,k) = (4,3)

Шаг :4

Подставим значения h,k в формулу

r² = (x — h)² + (y — k)²
r² = (2 — 4)² + (2 — 3)²
r² = (-2)² + (-1)²
r² = 5
r = 2.24

Шаг :5

Подставим значения h, k в уравнение окружности

(x — h)² + (y — k)²

Уравнение окружности = (x — 4)² + (y — 3)²

Ответ :

Координаты точки центра окружности c(h,k) = c(4,3)
Радиус окружности r = 2.24
Уравнение окружности = (x — 4)² + (y — 3)² = (2.24)²

людей нашли эту статью полезной. А Вы?

Источник