Как найти радиус описанной окружности куба

В данной публикации мы рассмотрим, чему равняется радиус сферы (шара), описанной около куба, а также как его можно вычислить, если известна длина ребра куба.

Примечание: Напомним, что вокруг любого куба можно описать шар.

Для начала начертим рисунок.

На данном чертеже:

все 8 вершин куба касаются шара – это их общие точки;
центр шара – точка O, которая также является точкой пересечения диагоналей куба.

Радиус шара (R), описанного вокруг куба, равняется половине его диагонали, т.е.:

Примечание: все диагонали куба равны.

Чтобы было понятнее, выполним диагональное сечение, т.е. отсечем часть шара вместе со вписанным в него кубом по диагонали куба (линия отреза проходит через точку O).

Таким образом, мы получим прямоугольник с описанной вокруг окружностью, радиус которой равняется половине диагонали прямоугольника.

Примечание: Диагонали прямоугольника равны между собой и одновременно являются диагоналями куба.

Формула расчета радиуса описанного шара через ребро куба

Если известна длина ребра куба (примем ее за “a”), радиус описанного вокруг него шара (R) вычисляется следующим образом:

Источник

Нахождение радиуса описанной вокруг куба сферы (шара)

Примечание: Напомним, что вокруг любого куба можно описать шар.

Для начала начертим рисунок.

На данном чертеже:

все 8 вершин куба касаются шара – это их общие точки;
центр шара – точка O, которая также является точкой пересечения диагоналей куба.

Радиус шара (R), описанного вокруг куба, равняется половине его диагонали, т.е.:

Примечание: все диагонали куба равны.

Примечание: Диагонали прямоугольника равны между собой и одновременно являются диагоналями куба.

Формула расчета радиуса описанного шара через ребро куба

Радиус описанной сферы куба

Свойства

Если описать вокруг куба сферу, то ее диаметр будет соединять противоположные вершины куба, образуя диагональ куба. Таким образом, радиус описанной сферы куба равен половине диагонали, следовательно, сама диагональ куба равна удвоенному радиусу описанной сферы. (рис.2.3) D=2R

Так как эта же диагональ связывает теоремой Пифагора в прямоугольном треугольнике диагональ стороны куба и ребро куба, то становится возможным вычислить и их через радиус описанной сферы куба, используя формулы диагонали. D=a√3 a=D/√3=2R/√3 a^2+d^2=D^2 (2R/√3)^2+d^2=(2R)^2 d^2=(8R^2)/3 d=√(8/3) R

Чтобы вычислить площадь грани куба, нужно рассмотреть ее в плоскости. Стороной куба является квадрат, поэтому его площадь равна стороне квадрата, то есть ребру куба, во второй степени. Площадь боковой поверхности куба состоит из четырех боковых граней-квадратов, а площадь полной поверхности – из шести граней, поэтому для их вычисления нужно умножить площадь одной грани на их количество. Чтобы найти площади куба через радиус сферы, описанной вокруг него, нужно подставить вместо ребра куба удвоенный радиус, деленный на корень из трех. S=a^2=(2R/√3)^2=(4R^2)/3 S_(б.п.)=4S=(16R^2)/3 S_(п.п.)=6S=(24R^2)/3

Объем куба, зная радиус описанной вокруг него сферы, вычисляется возведением в третью степень выражения для ребра куба. V=a^3=(2R/√3)^3=(8R^3)/(3√3)

Периметр куба, как умноженное на 12 ребро куба, представлено через радиус описанной вокруг сферы окружности в виде отношения радиуса, умноженного на 24, к корню из трех. P=12a=24R/√3

Чтобы вычислить радиус сферы, вписанной в куб, через радиус сферы, описанной около него, нужно разделить ребро куба на два, то есть разделить радиус описанной сферы на корень из трех. r=a/2=2R/(2√3)=R/√3

Как найти радиус окружности описанной вокруг грани куба

Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.

Свойства куба:

1. В кубе $6$ граней и все они являются квадратами.

2. Противоположные грани попарно параллельны.

3. Все двугранные углы куба – прямые.

4. Диагонали равны.

5. Куб имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.

6. Диагональ куба в $√3$ раз больше его ребра

7. Диагональ грани куба в $√2$ раза больше длины ребра.

Пусть $а-$длина ребра куба, $d-$диагональ куба, тогда справедливы формулы:

Площадь полной поверхности: $S_<п.п>=6а^2=2d^2$

Радиус сферы, описанной около куба: $R=/<2>$

Радиус сферы, вписанной в куб: $r=/<2>$

При увеличении всех линейных размеров куба в $k$ раз, его объём увеличится в $k^3$ раз.

При увеличении всех линейных размеров куба в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$-высота(она же боковое ребро);

$S_<п.п>$-площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Формулы вычисления объема и площади поверхности правильной пирамиды.

$h_a$ — высота боковой грани (апофема)

В основании лежат правильные многоугольники, рассмотрим их площади:

Для равностороннего треугольника $S=√3>/<4>$, где $а$ — длина стороны.
Квадрат $S=a^2$, где $а$ — сторона квадрата.

Задачи на нахождение объема составного многогранника:

Разделить составной многогранник на несколько параллелепипедов.
Найти объем каждого параллелепипеда.
Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

источники:

http://geleot.ru/education/math/geometry/calc/cube/radius_of_sphere

http://examer.ru/ege_po_matematike/teoriya/kub

Источник

Так как эта же диагональ связывает теоремой Пифагора в прямоугольном треугольнике диагональ стороны куба и ребро куба, то становится возможным вычислить и их через радиус описанной сферы куба, используя формулы диагонали.
D=a√3
a=D/√3=2R/√3
a^2+d^2=D^2
(2R/√3)^2+d^2=(2R)^2
d^2=(8R^2)/3
d=√(8/3) R

Чтобы вычислить площадь грани куба, нужно рассмотреть ее в плоскости. Стороной куба является квадрат, поэтому его площадь равна стороне квадрата, то есть ребру куба, во второй степени. Площадь боковой поверхности куба состоит из четырех боковых граней-квадратов, а площадь полной поверхности – из шести граней, поэтому для их вычисления нужно умножить площадь одной грани на их количество. Чтобы найти площади куба через радиус сферы, описанной вокруг него, нужно подставить вместо ребра куба удвоенный радиус, деленный на корень из трех.
S=a^2=(2R/√3)^2=(4R^2)/3
S_(б.п.)=4S=(16R^2)/3
S_(п.п.)=6S=(24R^2)/3

Источник

Куб. Формулы, признаки и свойства куба

Определение.

Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.

Определение. Грань куба — это часть плоскости, ограниченная сторонами квадрата.

— куб имеет шесть граней;

— каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;

— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.

Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.

— куб имеет двенадцать ребер;

— каждый конец ребра соединен с двумя соседними ребрами под прямым углом;

— ребра куба имеют одинаковую длину.

Определение. Вершина куба — это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.

— куб имеет восемь вершин;

— каждая вершина образована только тремя гранями и тремя ребрами.

Определение. Центр грани куба (O₁) — это равноудалена точка от всех ребер грани куба.

Определение. Центр куба (O) — это равноудалена точка от всех граней куба.

Определение. Ось куба (i) — это прямая, проходящая через центр куба и центры двух параллельных граней куба.

— куб имеет три оси;

— оси куба взаимно перпендикулярны.

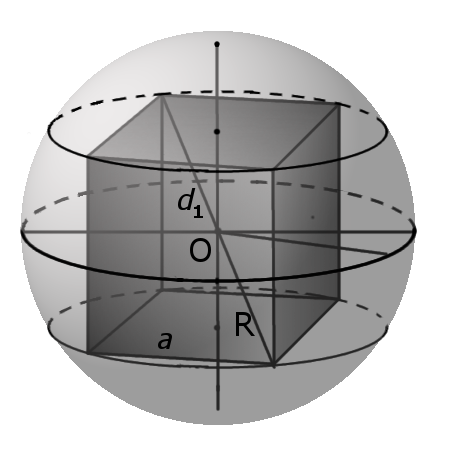
Определение. Диагональ куба (d₁) — отрезок, который соединяет противоположные вершины куба и проходит через центр куба.

— куб имеет четыре диагонали;

— диагонали куба пересекаются и делятся пополам в центре куба;

— диагонали куба имеют одинаковую длину.

Формула. Диагональ куба d₁ через длину ребра a:

d₁ = a√3

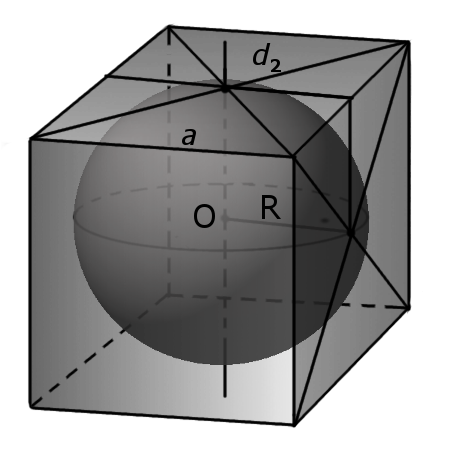
Определение. Диагональ грани куба (d₂) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.

Формула. Диагональ грани d₂ через длину ребра a:

d₂ = a√2

Определение. Объём куба — это совокупность всех точек в пространстве, ограниченные гранями куба.

Формула. Объём куба через длину ребра a:

V = a³

Формула. Объём куба через длину диагонали куба d₁:

Определение. Площадь поверхности куба — это совокупность плоскостей всех граней.

Формула. Площадь поверхности куба через длину ребра a:

S = 6a²

Определение. Периметр куба — это совокупность длин всех ребер куба.

Формула. Периметр куба P через длину ребра a:

P = 12a

Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

— все шесть граней куба являются касательными плоскостями к вписанной сферы;

— радиус вписанной сферы равен половине длины ребра a.

Формула. Радиус вписанной сферы r через длину ребра a:

Формула. Объема вписанной сферы V через длину ребра a:

Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.

— радиус описанной сферы равен половине длины диагонали (d₁) куба.

Формула. Радиус описанной сферы R через длину ребра a:

Формула. Объема сферы описанной вокруг куба V через длину ребра a:

Свойства куба

1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.

2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.

Координаты вершин куба

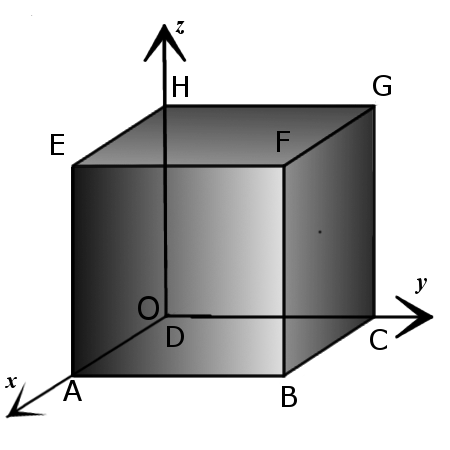
1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:

A(a, 0, 0),
B(a, a, 0),
C(0, a, 0),
D(0, 0, 0),
E(a, 0, a),
F(a, a, a),
G(0, a, a),
H(0, 0, a).

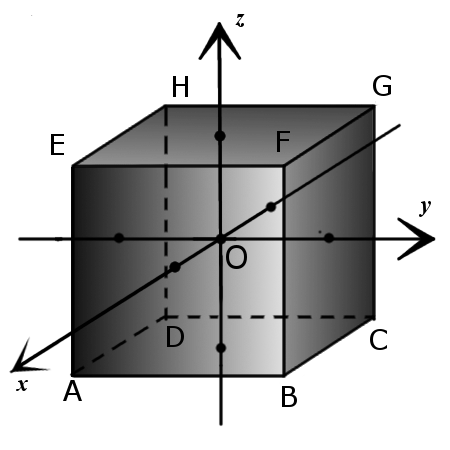
2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:

A(a, —a, —a),
B(a, a, —a),
C(-a, a, —a),
D(-a, —a, —a),
E(a, —a, a),
F(a, a, a),
G(-a, a, a),
H(-a, —a, a).

Определение. Единичный куб — это куб, у которого длина ребер равна единице.

Пересечение куба плоскостью

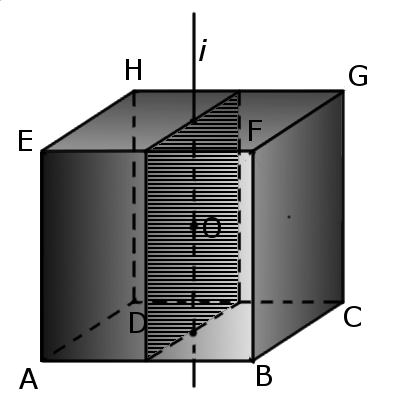
1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.

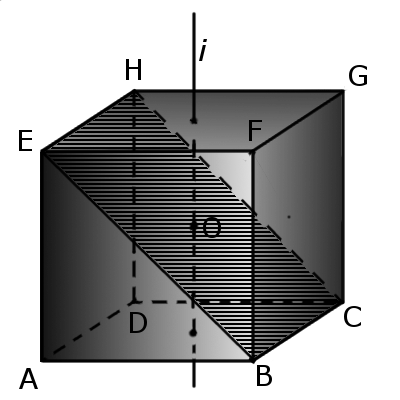
2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a²√2. Эта плоскость делит куб две равные призмы.

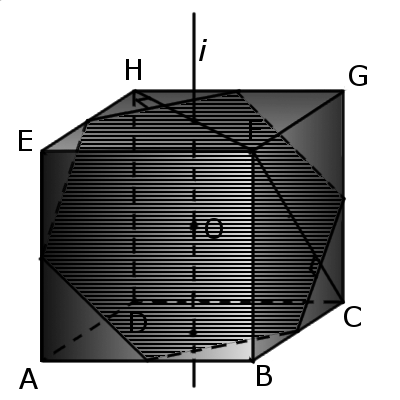
3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a²(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.

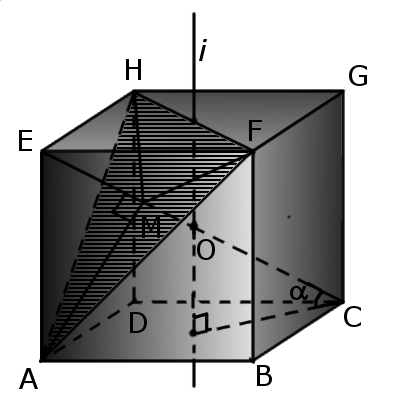
4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a²√3/2 и объемом большей части — 5a³/6 и меньшей — a³/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.

Источник

Нахождение радиуса описанной вокруг куба сферы (шара)

Радиус описанной сферы куба

Свойства