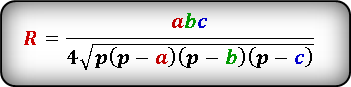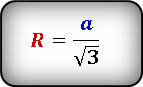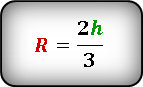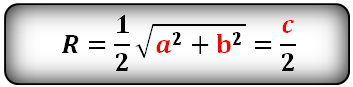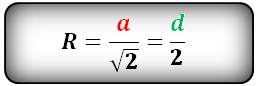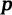
Формула радиуса описанной окружности треугольника ( R ) :



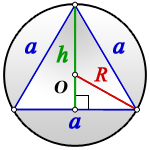
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
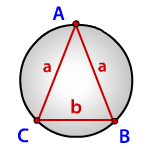
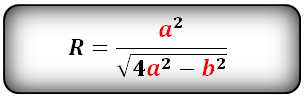
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Формула радиуса описанной окружности равнобедренного треугольника(R):
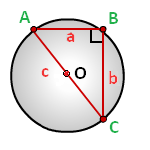
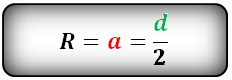
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a, b — катеты прямоугольного треугольника
c — гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
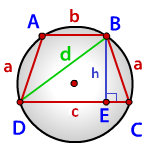
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
p — полупериметр треугольника DBC
p = (a+d+c)/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
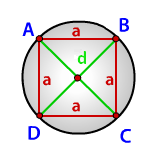
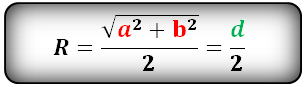
Радиус описанной окружности квадрата равен половине его диагонали
a — сторона квадрата
d — диагональ
Формула радиуса описанной окружности квадрата (R):
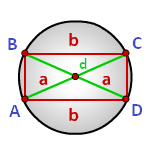
Радиус описанной окружности прямоугольника равен половине его диагонали
a, b — стороны прямоугольника
d — диагональ
Формула радиуса описанной окружности прямоугольника (R):
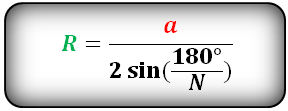
a — сторона многоугольника
N — количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
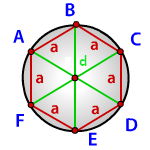
a — сторона шестиугольника
d — диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Радиус описанной окружности правильного многоугольника, формула
|
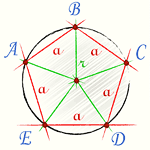
Правильный многоугольник — это многоугольник с равными сторонами и углами. Угол между двумя соседними вершинами правильного n-угольника равен: [AOB = α = frac{360°}{n}] |
 |
 |
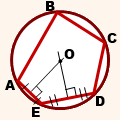
Построим треугольник AOB отдельно. Об этом треугольнике мы знаем: он равнобедренный, и бедра этого треугольника это радиусы описанной окружности правильного многоугольника. Также нам известна длина основания a этого треугольника — которое является стороной исходного правильного многоугольника. |
Также известен угол между радиусами R — по формуле (1).
Опустим высоту на основание и рассмотрим получившийся прямоугольный треугольник.
При помощи тригонометрических функций острого угла получим:
[sinBig(frac{360°}{2n}Big) = frac{a}{2R}]
отсюда получим формулу радиуса описанной окружности правильного многоугольника:
[R = frac{a}{2 sin(frac{360°}{2n})}]
(a — сторонa правильного многоугольника; n — число сторон правильного многоугольника; R — радиус описанной окружности правильного многоугольника)
Вычислить, найти радиус описанной окружности правильного многоугольника по формуле (3)
Радиус описанной окружности правильного многоугольника |
стр. 251 |
|---|
В публикации представлена формула, с помощью которой можно найти радиус окружности, описанной около правильного многоугольника, а также приведен пример решения задачи для лучшего понимания представленного материала.
- Формула расчета радиуса окружности
- Пример задачи
Формула расчета радиуса окружности
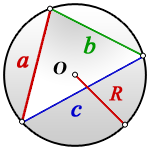
На рисунке изображен правильный шестиугольник с описанной вокруг него окружностью, но формула ниже подходит для любого правильного n-угольника.
где a – длина стороны.
Примечание: зная радиус описанного круга можно найти сторону равностороннего n-угольника (формула выводится из представленной выше):
Пример задачи
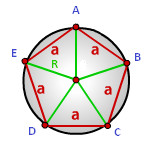
Дан правильный пятиугольник с длиной стороны 8 см. Вычислите радиус описанной около данной фигуры окружности.
Решение:
Применим соответствующую формулу, подставив в нее известное нам значение.
Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.
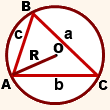
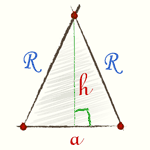
Радиус описанной окружности для произвольного треугольника
Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):
где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.
Центр описанной окружности лежит:
у остроугольного треугольника — внутри треугольника;
у прямоугольного — на середине гипотенузы;
у тупоугольного — вне треугольника, напротив тупого угла.
Радиус описанной окружности для прямоугольного треугольника
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:
Окружность, описанная около многоугольника
Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.
Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.
Радиус окружности, описанной около правильного многоугольника
Формула радиуса описанной окружности для правильного многоугольника
где a — длина стороны многоугольника, n — количество его сторон.
Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.
Радиус описанной окружности правильного треугольника

Если без иррациональности в знаменателе —
У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:
Радиус описанной окружности квадрата
Формула радиуса описанной окружности для квадрата
Если без иррациональности в знаменателе —
Радиус описанной окружности правильного шестиугольника
Формула радиуса описанной окружности для правильного шестиугольника
Радиус описанной окружности правильного многоугольника
a — сторона многоугольника
N — количество сторон многоугольника
Формула радиуса описанной окружности правильного многоугольника, ( R ):
Калькулятор — вычислить, найти радиус описанной окружности правильного многоугольника
Нахождение радиуса описанной вокруг правильного многоугольника окружности
В публикации представлена формула, с помощью которой можно найти радиус окружности, описанной около правильного многоугольника, а также приведен пример решения задачи для лучшего понимания представленного материала.
Формула расчета радиуса окружности
На рисунке изображен правильный шестиугольник с описанной вокруг него окружностью, но формула ниже подходит для любого правильного n-угольника.
где a – длина стороны.
Примечание: зная радиус описанного круга можно найти сторону равностороннего n-угольника (формула выводится из представленной выше):
Пример задачи
Дан правильный пятиугольник с длиной стороны 8 см. Вычислите радиус описанной около данной фигуры окружности.
Решение:
Применим соответствующую формулу, подставив в нее известное нам значение.
Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Нахождение радиуса описанной вокруг правильного многоугольника окружности
http://skysmart.ru/articles/mathematic/radius-okruzhnosti

2.png)