В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.
-
Формулы расчета радиуса сферы (шара)
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
- Правильная шестиугольная пирамида
Формулы расчета радиуса сферы (шара)
Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.
Правильная треугольная пирамида
На этом рисунке и чертежах далее:
- a – ребро основания пирамиды;
- h – высота фигуры.
Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:
Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:
Правильная четырехугольная пирамида
Радиус (R) описанной сферы/шара вычисляется следующим образом:
Правильная шестиугольная пирамида
Формула для нахождения радиус (R) сферы/шара выглядит так:
В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая — тетраэдра (см. ниже). Ссылки на примеры решения задач приведены в конце урока.
Определение
Правильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.
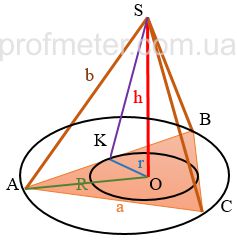
На рисунке обозначены:
ABC — Основание пирамиды
OS — Высота
KS — Апофема
OK — радиус окружности, вписанной в основание
AO — радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO — двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)
Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).
Свойства правильной треугольной пирамиды:
- боковые ребра правильной пирамиды равны
- все боковые грани правильной пирамиды являются равнобедренными треугольниками
- в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
- если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (пи делить на 3 или 60 градусов ).
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
- вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан
Формулы для правильной треугольной пирамиды
Формула объема правильной треугольной пирамиды:
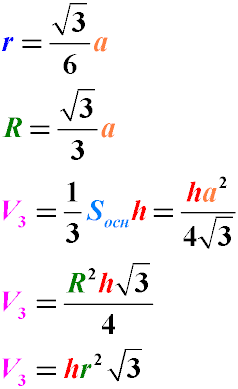
где
V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник
h — высота пирамиды
a — длина стороны основания пирамиды
R — радиус описанной окружности
r — радиус вписанной окружности
Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды.
Примеры решения задач:
- Нахождение периметра правильной треугольной пирамиды
- Вычисление объема
- Нахождение площади поверхности
Тетраэдр
Частным случаем правильной треугольной пирамиды является тетраэдр.
Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.
У тетраэдра:
- Все грани равны
- 4 грани, 4 вершины и 6 ребер
- Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны
Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине)
Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра)
Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности).
Тетраэдр обладает следующими свойствами:
- Все медианы и бимедианы тетраэдра пересекаются в одной точке
- Эта точка делит медианы в отношении 3:1, считая от вершины
- Эта точка делит бимедианы пополам
Площадь, объем, высота, радиус вписанной и описанной окружности и другие формулы для тетраэдра

См. пример задачи: формулы и свойства тетраэдра.
0
Пирамида с равнобедренным треугольником в основании |
Описание курса
| Периметр основания правильной треугольной пирамиды
�������
������� ��������� ���������� ����������� �������� ����� a, ������� ����� b. ������� ������ ���������� ����.
�������
������ ������. ����� DM ─ ������ ������ ���������� ����������� �������� ABCD, R ─ ������� ������. ��������� �������� ����������, ����� ţ ��������� ����� ����� �� ������ DM (���. 1). ���������� ������� �������� ����������, ���������� ����� ������ DM � ����� C (���. 2). ������� ���������� ������� R � ������� �� ������ DM, ���������� ����� ����� D � C. ��������� CM �� ����� M �� ����������� � ����������� � ����� C₁. ����� R ─ ������ ����������, ��������� ����� ��������������� ������������ CDC₁, � �������
| C₁D = CD = b, CC₁ = 2CM = | . |
�� �������������� ������������ CDM �������, ���
�������
�������������,
������ ������. ����� O ─ ����� �����, ��������� ����� ������ ���������� ����������� �������� ABCD � �������� D. ��������� �������� ����������, ����� O ����� �� ţ ������ DM. �� ������������� ������������� DMC � OMC �������, ���
���� ����� O ����� �� ������� DM (���. 1), �� OM + OD = DM, ���
����� ���������� ���������:
�������� ����� ������, ����� ����� O ����� �� ����������� ������ DM �� ����� M (���. 3). ����� OD = OM + DM, ���
������
������ ������. ����� DM ─ ������ ������ ���������� ����������� �������� ABCD, R ─ ������� ������. ��������� �������� ����������, ����� ţ ��������� ����� ����� �� ������ DM (���. 1). ���������� ������� �������� ����������, ���������� ����� ������ DM � ����� C (���. 4). ������� ���������� ������� R � ������� �� ������ DM, ���������� ����� ����� D � C. ��������� DM �� ����� M �� ����������� � ����������� � ����� D₁. ����� ∠DCD₁ = 90°. ������� DM · MD₁ = MC², ���
������ �������, ���
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 8361 |
3.4. Вписанные и описанные многогранники
Среди множества выпуклых многогранников выделим два важных семейства: вписанные и описанные многогранники.
Определение 22
Выпуклый многогранник называют вписанным, если все его вершины лежат на сфере. Эта сфера называется описанной для рассматриваемого многогранника.
Определение 23
Выпуклый многогранник называют описанным, если все его грани касаются сферы. Эта сфера называется вписанной для рассматриваемого многогранника.
Очевидно сходство введённых понятий с известными из курса планиметрии понятиями вписанных и описанных многоугольников, описанных и вписанных окружностей.
Не любой многогранник является вписанным или описанным, однако верны следующие две теоремы, аналогичные соответствующим теоремам про треугольник.
Теорема 3.4 (об описанной сфере треугольной пирамиды)
Треугольная пирамида имеет единственную описанную сферу.
Рис. 73
Доказательство. Рассмотрим треугольную пирамиду ABCD (рис. 73). Построим плоскости, перпендикулярные соответственно рёбрам AB, AC и AD и проходящие через их середины. (Геометрическим местом точек пространства, равноудалённых от концов некоторого отрезка, является плоскость, перпендикулярная этому отрезку и проходящая через его середину. Докажите это самостоятельно.) Обозначим через O точку пересечения этих плоскостей. (Такая точка существует, и она единственна. Докажем это. Возьмём первые две плоскости. Они пересекаются, поскольку перпендикулярны непараллельным прямым. Обозначим прямую, по которой пересекаются первые две плоскости, через l. Эта прямая l перпендикулярна плоскости ABC. Плоскость, перпендикулярная AD, не параллельна l и не содержит её, поскольку в противном случае прямая AD перпендикулярна l, т. е. лежит в плоскости ABC.) Точка O равноудалена от точек A и B, A и C, A и D, значит, она равноудалена ото всех вершин пирамиды ABCD, т. е. сфера с центром в O соответствующего радиуса является описанной сферой для пирамиды ABCD.
Итак, мы доказали существование для пирамиды ABCD описанной сферы. Осталось доказать её единственность. Центр любой сферы, проходящей через вершины пирамиды, равноудалён от этих вершин, значит, он принадлежит плоскостям, которые перпендикулярны рёбрам пирамиды и проходят через середины этих рёбер. Следовательно, центр такой сферы совпадает с точкой O.
Теорема доказана. ▼
Отметим, что при этом мы доказали, что все серединные перпендикуляры к рёбрам пирамиды пересекаются в одной точке.
Теорема 3.5 (о вписанной сфере треугольной пирамиды)
У любой треугольной пирамиды существует единственная вписанная сфера.
Рис. 74
Доказательство. Рассмотрим треугольную пирамиду ABCD (рис. 74). Проведём биссекторные плоскости её двугранных углов с рёбрами AB, AC и BC. Эти плоскости имеют единственную общую точку (подумайте почему). Обозначим её через Q. Точка Q равноудалена от всех граней пирамиды. (Она равноудалена от ABC и ABD, ABC и ADC, ABC и CBD.) Значит, сфера соответствующего радиуса с центром в точке Q является вписанной в пирамиду ABCD. Единственность этой сферы доказывается так же, как и в предыдущей теореме. ▼
Как и в предыдущем случае, мы доказали, что все шесть биссекторных плоскостей треугольной пирамиды пересекаются в одной точке.
Замечание. Понятия вписанной и описанной сферы могут относиться также к конусу и цилиндру. Любой конус имеет описанную и вписанную сферы. Если провести осевое сечение конуса, то эта плоскость пересечёт описанную и вписанную сферы по большим окружностям этих сфер, причём получившиеся окружности будут соответственно описаны или вписаны в осевое сечение конуса. Цилиндр, как и конус, всегда имеет описанную сферу. Но в отличие от конуса вписать сферу можно не во всякий цилиндр, а лишь в цилиндр с квадратным осевым сечением.
|
|
|
1(в). Найдите радиусы описанного и вписанного шаров для правильного тетраэдра с ребром a. |
|
2(в). Найдите ребро куба, вписанного в сферу радиуса R. |
|
3(в). Докажите, что если около параллелепипеда можно описать сферу, то этот параллелепипед — прямоугольный. |
|
4(в). Имеется правильная пирамида со стороной основания a и боковым ребром b. Найдите радиус: а) описанной сферы; б) вписанного шара; в) сферы, касающейся всех рёбер пирамиды; г) сферы, касающейся рёбер основания и продолжений боковых рёбер; д) радиус сферы, которая касается основания и боковых рёбер. Каждый пункт решите для пирамиды следующего вида: 1) четырёхугольной; 2) треугольной; 3) шестиугольной. |
|
5(в). Найдите радиус описанного и вписанного шаров для конуса с радиусом основания r и высотой h. |
|
6.Около шара описаны цилиндр и конус, осевым сечением которого является прямоугольный треугольник. Найдите отношение образующих цилиндра и конуса. |
|
7(в). Найдите радиус сферы, описанной около правильной n-угольной призмы с высотой h и стороной основания a. |
|
8(в). В основании правильной треугольной призмы лежит треугольник со стороной 1. Найдите боковое ребро призмы, если известно, что в неё можно вписать шар. |
|
9(т). Известно, что в заданную призму можно вписать шар. Найдите площадь её боковой поверхности, если площадь основания равна S. |
|
10(т). Плоскость проходит на расстоянии a от центра единичной сферы. Найдите ребро куба, одна грань которого лежит в этой плоскости, а вершины противоположной грани находятся на сфере. |
|
11(в). Около призмы можно описать сферу. Докажите, что основание призмы — многоугольник, около которого можно описать окружность. Найдите радиус этой окружности, если высота призмы h, а радиус описанной около неё сферы равен R. |
|
12(в). Основанием пирамиды служит многоугольник, около которого можно описать окружность. Докажите, что существует сфера, описанная около этой пирамиды. Найдите радиус этой сферы, если радиус окружности, описанной около основания пирамиды, равен r, её высота h, а основание высоты совпадает с вершиной основания пирамиды. |
|
13.В треугольной пирамиде ABCD ребро AB равно a, а углы ACB и ADB — прямые. Найдите радиус описанной около этой пирамиды сферы. |
|
14.Найдите ребро куба, одна грань которого принадлежит основанию конуса, а остальные вершины расположены на его боковой поверхности. Радиус основания конуса равен r, его высота h. |
|
15.Через центр сферы радиуса R проведены три попарно перпендикулярные плоскости. Найдите радиус сферы, касающейся всех этих плоскостей и данной сферы. |
|
16.Осевым сечением конуса является правильный треугольник со стороной a. Через ось конуса проведены две перпендикулярные плоскости, которые делят конус на четыре части. Найдите радиус шара, вписанного в одну из этих частей. |
|
17.Внутри единичного куба находятся восемь равных шаров. Каждый шар вписан в один из трёхгранных углов куба и касается трёх шаров, соответствующих соседним вершинам. Найдите радиусы этих шаров. |
|
18(в). Четыре сферы радиуса R попарно касаются друг друга. Найдите радиус сферы, касающейся всех четырёх сфер. |
|
19.Два шара касаются друг друга и граней трёхгранного угла, все плоские углы которого прямые. Найдите отношение радиусов этих шаров. |
|
20(п). Докажите, что если в данный четырёхгранный угол можно вписать шар, то суммы противоположных плоских углов этого четырёхгранного угла равны. Докажите справедливость обратного утверждения: если суммы противоположных плоских углов четырёхгранного угла равны, то в него можно вписать шар. |
|
21(п). Дан трёхгранный угол OABC, в котором ∠BOC = a, ∠COA = b, ∠ AOB = g. Пусть вписанный в него шар касается грани BOC в точке K. Найдите ∠KOB. |
|
22(т). Треугольник ABC вписан в основание конуса, S — вершина конуса. В трёхгранном угле SABC двугранные углы с рёбрами SA, SB и SC равны соответственно x, y и z. Найдите угол между плоскостями SAB и SAO, где SO — высота данного конуса. |
|
23(т). Четырёхгранный угол OABCD (OA, OB, OC, OD — его рёбра) разделён плоскостью OAC на два трёхгранных угла. В каждый из полученных углов вписан шар. Эти шары касаются плоскости OAC в точках K и M. Найдите угол KOM, если ∠BOA = a, ∠DOA = b, ∠BOC = ∠COD. |
|
24(п). Докажите, что радиус шара, проходящего через точки пересечения медиан граней произвольного тетраэдра, в три раза меньше радиуса описанного около рассматриваемого тетраэдра шара. Используя этот факт, докажите, что в произвольном тетраэдре выполняется неравенство R ⩾ 3r, где R и r — соответственно радиусы описанного и вписанного шаров. |
|
25(т). Боковое ребро правильной четырёхугольной пирамиды равно l, а плоский угол при вершине равен a. Найдите радиус описанной около этой пирамиды сферы. |
Материал урока.
С пирамидой мы с
вами знакомились в курсе геометрии базовой школы. Давайте вспомним, какой
многогранник мы назвали пирамидой и основные элементы пирамиды.
Итак, рассмотрим
многоугольник A1A2…An и точку P, не лежащую в
плоскости этого многоугольника. Соединим точку ПЭ отрезками с вершинами
многоугольника. В итоге получим n треугольников:
PA1A2, PA2A3, …, PAnA1. Многогранник, составленный из n-угольника A1A2…An и этих n треугольников, называется пирамидой.
Многоугольник A1A2…An называется основанием пирамиды.
Треугольники PA1A2,
PA2A3, …,
PAnA1 называются боковыми
гранями пирамиды. Точка P – вершиной пирамиды,
а отрезки PA1, PA2,…,
PAn – ее боковыми
ребрами.
Пирамиду с вершиной
P и основанием A1A2…An называют n-угольной пирамидой и обозначают так: PA1A2…An.
Отрезок,
соединяющий вершину пирамиды с плоскостью ее основания и перпендикулярный к
этой плоскости, называется высотой пирамиды.
Объединение боковых граней называется боковой
поверхностью пирамиды, а объединение всех граней называется полной
поверхностью пирамиды. Тогда площадью боковой поверхности пирамиды
называется сумма площадей ее боковых граней. А площадью полной поверхности
пирамиды называется сумма площадей всех ее граней.
Пирамида в зависимости от того какой многоугольник
лежит в основании имеет свое название. Если в основании лежит треугольник, то
пирамида называется треугольной. Если четырехугольник – то четырехугольной
пирамидой. А если n-угольник, то n-угольной
пирамидой.
Решим задачу.
Задача. Основанием
пирамиды является ромб, сторона которого равна , а одна из
диагоналей равна . Найти длину
боковых ребер пирамиды, если высота пирамиды проходит через точку пересечения
диагоналей основания и равна .
Решение.
Ответ. ,
см.
Давайте дадим определение
правильной пирамиды.
Пирамида
называется правильной, если ее основание – правильный многоугольник, а
отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется
апофемой.
На сегодняшнем
уроке мы подробно рассмотрим правильные пирамиды.
Сейчас давайте
попробуем доказать одно из свойств правильной пирамиды. А именно
докажем, что все боковые ребра правильной пирамиды равны, а боковые грани
являются равными равнобедренными треугольниками.
Рассмотрим
правильную пирамиду PA1A2…An. Сначала докажем, что все боковые ребра этой
пирамиды равны. Проведем высоту пирамиды.
Поскольку
основанием правильной пирамиды является правильный многоугольник, значит,
вокруг основания правильной пирамиды можно описать окружность. Тогда каждое
боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного
треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания
окружности. Например, если рассмотреть треугольник OPA1,
то OP равно h, OA1 равно R.
Таким образом, мы
доказали, что боковые ребра правильной пирамиды равны. А значит, боковые грани
правильной пирамиды – это равнобедренные треугольники. Поскольку в основании
лежит правильный многоугольник, значит, основания боковых граней равны между
собой. То есть боковые грани равны между собой по трем сторонам.
Что и
требовалось доказать.
Теперь давайте
сформулируем и докажем теорему о площади боковой поверхности правильной
пирамиды.
Площадь боковой
поверхности правильной пирамиды равна половине произведения периметра основания
на апофему.
Доказательство.
Запишем формулу для
вычисления площади боковой поверхности правильной пирамиды.
Мы уже доказали,
что боковые грани правильной пирамиды – равные равнобедренные треугольники.
Высоты этих треугольников равны апофеме пирамиды. Тогда площадь боковой грани
находится по формуле .
Подставим эти
площади в формулу площади боковой поверхности. Вынесем половину апофемы за
скобки, тогда в скобках получим периметр основания.
Что и
требовалось доказать.
Решим несколько
задач.
Задача. Радиус
окружности, вписанной в основание правильной четырехугольной пирамиды, равен , высота
пирамиды равна . Найти
площадь боковой поверхности пирамиды.
Решение.
Ответ. 60 м2
Решим еще одну
задачу.
Задача. Радиус
окружности, описанной около основания правильной треугольной пирамиды, равен .
. Найти длину
апофемы.
Решение.
Ответ. 4 м
Подведем итоги
урока.
Сегодня на уроке мы
вспомнили, какая фигура называется пирамидой. Какие пирамиды называются
правильными. Познакомились со свойствами правильных пирамид. Решили несколько
задач.








