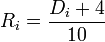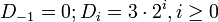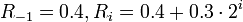Как найти радиус орбиты планет - Исправление недочетов и поиск решений вместе с Examum.ru

Правило Тициуса — Боде

И. Д. Тициус

И. Э. Боде

Правило Тициуса — Боде (известно также как закон Боде) представляет собой эмпирическую формулу, приблизительно описывающую расстояния между планетами Солнечной системы и Солнцем (средние радиусы орбит). Правило было предложено И. Д. Тициусом в 1766 г. и получило известность благодаря работам И. Э. Боде в 1772 г.

Правило формулируется следующим образом.

К каждому элементу последовательности 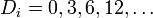прибавляется 4, затем результат делится на 10. Полученное число считается радиусом в астрономических единицах. То есть,

$R_i = {D_i + 4 over 10}$

Последовательность D_i — геометрическая прогрессия, кроме первого числа. То есть, $D_{-1} = 0; D_i = 3 cdot 2^i, i geq 0$

Эту же формулу можно записать по-другому:

$R_{-1}=0.4, R_{i} = 0.4 + 0.3 cdot 2^i$

Встречается также другая формулировка:

Для любой планеты расстояние от неё до самой внутренней планеты (Меркурия) в два раза больше, чем расстояние от предыдущей планеты до внутреннй планеты:

${R_i - R_{Mercury}} = 2 cdot left( {R_{i-1} - R_{Mercury}} right)$

Результаты вычислений приведены в таблице. Видно, что этой закономерности соответствует и пояс астероидов, а вот Нептун, наоборот, из закономерности выпадает, причём его место странным образом занимает Плутон, который по решению XXVI Ассамблеи МАС планетой вообще не является.

Планета	i	k	Радиус орбиты (а. е.)	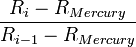${R_i - R_{Mercury}}over{R_{i-1} - R_{Mercury}}$
по правилу	фактический
Меркурий	−1	0	0,4	0,39
Венера	0	1	0,7	0,72
Земля	1	2	1,0	1,00	1,825
Марс	2	4	1,6	1,52	1,855
Пояс астероидов	3	8	2,8	в сред. 2,2—3,6	2,096 (по орбите Цереры)
Юпитер	4	16	5,2	5,20	2,021
Сатурн	5	32	10,0	9,54	1,9
Уран	6	64	19,6	19,22	2,053
Нептун	выпадает	30,06	1,579
Плутон	7	128	38,8	39,5	2,078 (по отношению к Урану)
Эрида	8	256	77,2	67,7

Когда Тициус впервые сформулировал это правило, ему удовлетворяли все известные в то время планеты (от Меркурия до Сатурна), имелся лишь пропуск на месте пятой планеты. Тем не менее, правило не привлекло большого внимания до тех пор, пока в 1781 году не был открыт Уран, который почти точно лёг на предсказанную последовательность. После этого Боде призвал начать поиски недостающей планеты между Марсом и Юпитером. Именно в том месте, где должна была располагаться эта планета, была обнаружена Церера. Это вызвало большое доверие к правилу Тициуса — Боде среди астрономов, которое сохранялось до открытия Нептуна. Когда выяснилось, что, кроме Цереры, примерно на том же расстоянии от Солнца находится множество тел, формирующих пояс астероидов, была выдвинута гипотеза, что они образовались в результате разрушения планеты (Фаэтона), которая раньше находилась на этой орбите.

Правило не имеет конкретного математического и аналитического (через формулы) объяснения исходя только из теории гравитации — мешает так называемая проблема взаимодействия трех тел.

Но наиболее вероятное объяснение заключается в следующем. Уже на стадии формирования Солнечной системы в результате гравитационных возмущений, вызванных протопланетами и их резонансом с нетвердым Солнцем (при этом возникают приливные силы и энергия вращения тратится на приливное ускорение или скорее замедление — подробнее смотри на английском tidal acceleration)сформировалась регулярная структура из чередующихся областей, в которых могли или не могли существовать стабильные орбиты согласно правилам орбитальных резонансов (т.е. отношение радиусов орбит соседних планет равных 1/2, 3/2, 5/2, 3/7 и т.п.). Подробнее эту версию смотри на странице http://elementy.ru/trefil/21221?context=20444&discuss=21221.

Резонансным орбитам сейчас в основном соответствуют планеты или группы астероидов, которые постепенно (за десятки и сотни миллионов лет) выходили на эти орбиты. В случаях когда планеты (астероиды и планетоиды за Плутоном) не расположены на стабильных орбитах (как Нептун) или не расположены в плоскости эклиптики (как Плутон) наверняка в ближайшем (относительно сотни миллионов лет) прошлом имели место инциденты нарушавшие их орбиты (столкновение, близкий пролет массивного внешнего тела). Со временем (быстрее к центру системы и медленне на окраинах системы) они неизбежно займут стабильные орбиты, если им не помешают новые инциденты.

Наличие стабильных орбит вызванных резонансами между телами системы впервые численно смоделированно (компьютерная симуляция движения точечных взаимодействующих масс вокруг резонирующего центра — Солнца, представленного как две точечные массы с упругой связью) и приведено в сравнении с реальными астрономическими данными в работах 1998-99 годов профессора Рену Малхотра Renu Malhotra. Смотри ссылки ниже и домашнюю страницу автора: http://www.lpl.arizona.edu/~renu/ Само существование резонансных орбит орбитальный резонанс в нашей системе подтверждается экспериментальными данными по распределению астероидов по радиусу орбиты и плотности объектов KBO пояса Койпера по радиусу их орбиты. Смотри фильм (3 Мб) с докладом того же автора (в котором она приводит графики распределения астероидов по орбитам) http://www.lpl.arizona.edu/~renu/malhotra_presentations/09-migrating_planets.mov , а также графики распределения планетоидов KBO или так называемых Plutinos/plutoids плутино (http://en.wikipedia.org/wiki/File:TheKuiperBelt_classes-en.svg) на странице посвященной объектам пояса Койпера в английской версии: http://en.wikipedia.org/wiki/Kuiper_belt

Три планеты Солнечной системы — Юпитер, Сатурн и Уран — имеют систему спутников, которые, возможно, сформировались в результате таких же процессов, как и в случае самих планет. Эти системы спутников образуют регулярные структуры, на основе орбитальных резонансов, которые, правда, не подчиняются правилу Тициуса — Боде. С другой стороны другие системы спутников планет так же могут быть возмущены внешними инцедентами в недавнем прошлом и находится в данный момент на пути к стабильным орбитам.

Сравнивая структуру стабильных орбит планет Солнечной системы с электронными оболочками простейшего атома можно обнаружить некоторое подобие, хотя в атоме электрон практически мгновенно переходит только между стабильными орбитами (электронными оболочками), а в планетарной системе выход на стабильные орбиты занимает десятки и сотни миллионов лет.

Ссылки

http://elementy.ru/trefil/21221?context=20444&discuss=21221
Malhotra, R., Migrating Planets, Scientific American 281(3):56-63 (1999)
Hahn, J.M., Malhotra, R., Orbital evolution of planets embedded in a massive planetesimal disk, AJ 117:3041-3053 (1999).
Malhotra, R., Chaotic planet formation, Nature 402:599-600 (1999).
Malhotra, R., Orbital resonances and chaos in the Solar system, in Solar System Formation and Evolution, Rio de Janeiro, Brazil, ASP Conference Series vol. 149 (1998). Preprint
Showman, A., Malhotra, R., The Galilean Satellites, Science 286:77 (1999).
Планетарные орбиты и протон. «Наука и жизнь» № 1, 1993.

Wikimedia Foundation.
2010.

Источник

Солнечная система как гравитационный атом Бора — представление Солнечной планетной системы в виде модели «гравитационного атома Бора» с радиусом произвольной орбиты в общем виде:

${displaystyle r_{n}=n^{2}cdot r_{1}, }$

где ${displaystyle r_{1}=r_{1T}=6.4554cdot 10^{9}}$ м — радиус первой орбиты (не обязательно заполненной) планет земной группы (), и
${displaystyle r_{1}=r_{1J}=1.527cdot 10^{11}}$ м — радиус первой орбиты (заполнен обязательно, правда планетой другого типа) внешних планет ().

История

В астрономии известно правило Тициуса — Боде, которое представляет собой эмпирическую формулу, приблизительно описывающую расстояния между планетами Солнечной системы и Солнцем (средние радиусы орбит). Правило было предложено И. Д. Тициусом в 1766 г. и получило известность благодаря работам И. Э. Боде в 1772 г. ^[1]:

${displaystyle r_{n}/r_{1}=0.4+0.3cdot 2^{n}, }$

где , а расстояния измеряются в астрономических единицах. Долгое время эта математическая формула не имела физического обоснования, но с появлением квантовой физики денлались неоднократные попытки ее объяснения
^[2]
^[3]
^[4]
^[5].
Дело в том, что при рассмотрении атома Бора на начальном этапе делались попытки перенесения теории планетной системы на электронные орбиты атома. Но с появлением уравнения Шредингера и развития квантовой механики начался обратный процесс – перенесения квантовомеханических представлений на строение Солнечной системы.

Успех пришел только в конце 90-х годов 20-го века и связан с исследованием югославского физика Рубчича
^[6]
^[7]
^[8]
^[9]
А также бразильской группой космологов под руководством Карнейро
^[10]
^[11]
^[12]
и других
^[13].

Наиболее полно даный процесс представлен в сборнике статей
^[9].
В это же время был разработан т.н. «диффузный подход» к уравнению Шредингера для рассмотрения процесса создания Солнечной системы. Очевидно, что при таком подходе решения и масштабные константы «макроскопического уравнения Шредингера» получаются численным путем, что затрудняет рассмотрение данного вопроса.

Модель гравитационного квантования орбит

В общем случае момент импульса для произвольной планеты можно представить в виде:

${displaystyle J_{n}=m_{n}v_{n}r_{n}=m_{n}{sqrt {GMr_{n}}}, }$

где — гравитационная постоянная,
${displaystyle m_{n}}$ — масса планеты,
— масса звезды ( ${displaystyle Mgg m_{n}}$ ), а
${displaystyle r_{n}}$ — радиус орбиты планеты.

Предположим, что в этом случае макроскопической квантовой системы также можно воспользоватиься микроскопическим квантованием момента импульса (типа Бора- Зоммерфельда):

${displaystyle J_{n}=m_{n}{sqrt {GMr_{n}}}=ncdot {frac {H_{n}}{2pi }}, }$

где ${displaystyle H_{n}}$ — «макроскопический» квант действия для произвольной планеты (он зависит от — номера орбиты). Этот квант действия можно записать в виде:

${displaystyle {frac {H_{n}}{2pi m_{n}M}}=fcdot R_{HGS}, }$

где

${displaystyle R_{HGS}=2pi cdot {frac {G}{calpha _{S}}}={frac {h}{m_{S}^{2}}}=1.9157cdot 10^{-16}m^{2}/kgs }$

Унивесиальная постоянная, имеющая размерность гравитационного сопротивления (гравитационная постоянная фон Клитцинга), а
${displaystyle m_{S}}$ — масса масштаба Стони,
— гравитационный фактор коррекции, учитывающий макроскопические размеры квантовой системы.

В общем случае радиус орбиты произвольной планеты можно представить в виде:

${displaystyle r_{n}=(fcdot R_{HGS})^{2}{frac {M}{G}}cdot n^{2}=n^{2}cdot r_{1}, }$

где ${displaystyle r_{n}=(fcdot R_{HGS})^{2}{frac {M}{G}}}$ — радиус орбиты первой планеты (). Зная параметры орбит планетной системы, можно определить гравитационный фактор коррекции:

${displaystyle f={frac {1}{nR_{HGS}}}cdot {sqrt {frac {r_{n}G}{M}}} }$

Очевидно, что он зависит от массы центрального тела () и поэтому не может выступать в качестве фундаментальной постоянной. Совсем другое дело – радиус первой орбиты ${displaystyle r_{1}}$ , который должен быть фундаментальной константой по аналогии с обычным атомом Бора, где существует фундаментальный радиус Бора (масштаб):

${displaystyle a_{B}={frac {lambda _{N}}{2pi alpha _{S}}}={frac {l_{S}}{alpha _{S}}}=5.291767cdot 10^{-11} }$

Где ${displaystyle lambda _{N}}$ — комптоновская длина волны электрона, а ${displaystyle alpha _{S}=7.297352568cdot 10^{-03}}$ — силовая постоянная масштаба Стони (постоянная тонкой структуры Зоммерфельда).

Использование «диффузионного» уравнения Шредингера для планетной системы не предсказывает конкретное значение для «гравитационного радиуса Бора». Поэтому можно использовать непосредственно уравнение Шредингера для движения частицы с массой Планка ( ${displaystyle m_{P}}$ ), например в гравитационном поле другой планковской частицы. В этом случае мы получаем фундаментальное значение для гравитационного радиуса Бора в виде:

${displaystyle a_{BG}={frac {l_{P}}{alpha _{N}}}=9.22625cdot 10^{9} }$

где ${displaystyle l_{P}=1.61624cdot 10^{-35}}$ — длина Планка, а
${displaystyle alpha _{N}={frac {m_{N}^{2}}{2hcepsilon _{G}}}=1.75178cdot 10^{-45}}$ — силовая постоянная природного масштаба,
${displaystyle m_{N}}$ — масса электрона,
— постоянная Планка,
— скорость света и
${displaystyle epsilon _{G}=1/4pi G=1.1923148cdot 10^{9}kg*s^{2}/m^{3}}$ — диэлектрическая гравитационная постоянная.

Не трудно заметить, что первый радиус гравитационной орбиты для планет земной группы близок к значению:

${displaystyle r_{1T}=r_{BP}={frac {a_{BP}}{sqrt {2}}}=6.52394cdot 10^{9}}$

Т.е. определяется масштабом Планка! Гравитационный фактор коррекции в этом случае будет:

${displaystyle f_{1T}={frac {1}{R_{HGS}}}{sqrt {frac {r_{1T}G}{M}}}=2.44086 }$

При использовании уравнения Шредингера для движения частицы с массой Стони ( ${displaystyle m_{S}}$ ) в гравитационном поле другой частицы Стони, мы получаем следующее значение для гравитационного радиуса Бора масштаба Стони:

${displaystyle a_{BS}={frac {l_{S}}{alpha _{N}}}=1.08005cdot 10^{11} }$

где ${displaystyle l_{S}=1.89201cdot 10^{-34}}$ м – длина масштаба Стони. Но именно это значение радиуса орбиты имеет сегодня планета Венера! Далее, первый радиус орбиты внешних планет Солнечной системы равен значению:

${displaystyle r_{1J}=r_{BS}={sqrt {2}}a_{BS}={sqrt {frac {2}{alpha _{S}}}}a_{BP}=1.52742cdot 10^{11} }$

м,

Которое практически совпадает с современным значением для орбиты Земли!
Таким образом, внешние планеты Солнечной системы определяются масштабом Стони. Гравитационный фактор коррекции в этому случае будет:

${displaystyle f_{1J}={frac {1}{R_{HGS}}}{sqrt {frac {r_{1J}G}{M}}}=11.8105 }$

Для сравнения можно привести значение фактора коррекции для атома Бора:

${displaystyle f_{H}={frac {1}{2^{1/4}R_{HGS}}}{sqrt {{frac {a_{B}}{G}}{m_{pr}}}}=6.374567cdot 10^{18} }$

где ${displaystyle m_{pr}}$ — масса протона, а также для «планкионного атома»:

${displaystyle f_{P}={frac {1}{2^{1/4}R_{HGS}}}{sqrt {frac {a_{BP}G}{m_{P}}}}=2.33339cdot 10^{19} }$

Очевидно, что эти «микроскопические» значения очень сильно отличаются от «макроскопических». Другими словами, мы имеем значительное «ослабление» гравитационного фактора при переходе к макроскопическим квантовым системам.

Таблица 1. Внутренние планеты земного типа.

Название тела	Радиус тела, м	Радиус орбиты, м	Масса тела, кг		${displaystyle r_{1} }$ м
Меркурий	${displaystyle 2.425cdot 10^{6}}$	${displaystyle 5.79cdot 10^{10}}$	${displaystyle 3.311cdot 10^{23}}$	3	${displaystyle 6.4333cdot 10^{9}}$
Венера	${displaystyle 6.07cdot 10^{6}}$	${displaystyle 1.082cdot 10^{11}}$	${displaystyle 4.87cdot 10^{24}}$	4	${displaystyle 6.76250cdot 10^{9}}$
Земля	${displaystyle 6.371cdot 10^{6}}$	${displaystyle 1.496cdot 10^{11}}$	${displaystyle 5.976cdot 10^{24}}$	5	${displaystyle 5.9840cdot 10^{9}}$
Марс	${displaystyle 3.395cdot 10^{6}}$	${displaystyle 2.279cdot 10^{11}}$	${displaystyle 6.424cdot 10^{23}}$	6	${displaystyle 6.3306cdot 10^{9}}$

Планетарные параметры были взяты в справочнике Алена (1973)
^[14].

Таблица 2. Внешние планеты.

Название тела	Радиус тела, м	Радиус орбиты, м	Масса тела, кг		${displaystyle r_{1} }$ м
Юпитер	${displaystyle 7.13cdot 10^{7}}$	${displaystyle 7.783cdot 10^{11}}$	${displaystyle 1.899cdot 10^{27}}$	2	${displaystyle 1.94575cdot 10^{11}}$
Сатурн	${displaystyle 6.01cdot 10^{7}}$	${displaystyle 1.427cdot 10^{12}}$	${displaystyle 5.686cdot 10^{26}}$	3	${displaystyle 1.58555cdot 10^{11}}$
Уран	${displaystyle 2.45cdot 10^{7}}$	${displaystyle 2.8696cdot 10^{12}}$	${displaystyle 8.689cdot 10^{25}}$	4	${displaystyle 1.79350cdot 10^{11}}$
Нептун	${displaystyle 2.51cdot 10^{7}}$	${displaystyle 4.4966cdot 10^{12}}$	${displaystyle 1.03cdot 10^{26}}$	5	${displaystyle 1.79864cdot 10^{11}}$
Плутон	${displaystyle 3.2cdot 10^{6}}$	${displaystyle 5.9092cdot 10^{12}}$	${displaystyle 1.016cdot 10^{24}}$	6	${displaystyle 1.641444cdot 10^{11}}$

Квантовое гравитационное уравнение Шредингера

При описании планетной системы сегодня используется следующая форма записи уравнения Шредингера:

${displaystyle -{frac {hbar _{gr}^{2}}{2m}}{mathcal {5}}^{2}Psi -{frac {GmM}{r}}Psi =WPsi , }$

где — масса планеты, а — масса центральной звезды. При этом в жертву была принесена т.н. «гравитационная постоянная Планка, которая здесь перестала быть фундаментальной величиной:

${displaystyle {frac {hbar _{gr}^{2}}{hbar ^{2}}}={frac {M}{m_{P}}}({frac {m}{m_{N}}})^{2} }$

где ${displaystyle m_{P}}$ — масса Планка, а ${displaystyle m_{N}}$ — масса электрона. Дело в том, что в этом случае гравитационная постоянная Планка имеет различные значения для разных планет и звезд.

Более перспективном является следующая форма записи гравитационного уравнения Шредингера:

${displaystyle -{frac {hbar ^{2}}{2m_{x}}}{mathcal {5}}^{2}Psi -{frac {GmM}{r}}Psi =WPsi , }$

в которой используется концепция «малой виртуальной массы»:

${displaystyle m_{x}={frac {m_{P}m_{N}^{2}}{mM}} }$

Следует отметить, что оба подхода дают одинаковые результаты для масштабных значений гравитационного атома Бора. Действительно, гравитационный радиус Бора имеет значение:

${displaystyle r_{1}=a_{BG}={frac {hbar }{alpha _{N}m_{P}c}} }$

а гравитационная энергия связи Бора:

${displaystyle W_{BG}={frac {hbar ^{2}}{2m_{P}a_{BG}^{2}}} }$

где ${displaystyle alpha _{N}={frac {m_{N}^{2}}{2hcepsilon _{G}}}}$ — силовая постоянная гравитационного взаимодействия, а ${displaystyle epsilon _{G}={frac {1}{4pi G}}}$ — гравитационная «диэлектрическая постоянная».

Результаты расчета гравитационной постоянной Планка и «малой виртуальной массы» представлены в Таблицах 3,4:

Таблица 3. Внутренние планеты земного типа.

Название тела	Радиус тела, м	Радиус орбиты, м	Масса тела, кг		${displaystyle hbar _{gr} }$ Дж с	${displaystyle m_{x} }$ кг
Меркурий	${displaystyle 2.425cdot 10^{6}}$	${displaystyle 5.79cdot 10^{10}}$	${displaystyle 3.311cdot 10^{23}}$	3	${displaystyle 3.4747cdot 10^{72}}$	${displaystyle 2.7424cdot 10^{-122}}$
Венера	${displaystyle 6.07cdot 10^{6}}$	${displaystyle 1.082cdot 10^{11}}$	${displaystyle 4.87cdot 10^{24}}$	4	${displaystyle 5.1107cdot 10^{73}}$	${displaystyle 1.8645cdot 10^{-123}}$
Земля	${displaystyle 6.371cdot 10^{6}}$	${displaystyle 1.496cdot 10^{11}}$	${displaystyle 5.976cdot 10^{24}}$	5	${displaystyle 6.2714cdot 10^{73}}$	${displaystyle 1.5194cdot 10^{-123}}$
Марс	${displaystyle 3.395cdot 10^{6}}$	${displaystyle 2.279cdot 10^{11}}$	${displaystyle 6.424cdot 10^{23}}$	6	${displaystyle 6.7415cdot 10^{72}}$	${displaystyle 1.4135cdot 10^{-122}}$

Таблица 4. Внешние планеты.

Название тела	Радиус тела, м	Радиус орбиты, м	Масса тела, кг		${displaystyle hbar _{gr} }$ Дж с	${displaystyle m_{x} }$ кг
Юпитер	${displaystyle 7.13cdot 10^{7}}$	${displaystyle 7.783cdot 10^{11}}$	${displaystyle 1.899cdot 10^{27}}$	2	${displaystyle 1.9929cdot 10^{76}}$	${displaystyle 4.7815cdot 10^{-126}}$
Сатурн	${displaystyle 6.01cdot 10^{7}}$	${displaystyle 1.427cdot 10^{12}}$	${displaystyle 5.686cdot 10^{26}}$	3	${displaystyle 5.9671cdot 10^{75}}$	${displaystyle 1.5969cdot 10^{-125}}$
Уран	${displaystyle 2.45cdot 10^{7}}$	${displaystyle 2.8696cdot 10^{12}}$	${displaystyle 8.689cdot 10^{25}}$	4	${displaystyle 9.1185cdot 10^{74}}$	${displaystyle 1.0450cdot 10^{-124}}$
Нептун	${displaystyle 2.51cdot 10^{7}}$	${displaystyle 4.4966cdot 10^{12}}$	${displaystyle 1.03cdot 10^{26}}$	5	${displaystyle 1.0809cdot 10^{75}}$	${displaystyle 8.8156cdot 10^{-125}}$
Плутон	${displaystyle 3.2cdot 10^{6}}$	${displaystyle 5.9092cdot 10^{12}}$	${displaystyle 1.016cdot 10^{24}}$	6	${displaystyle 1.0662cdot 10^{73}}$	${displaystyle 8.9371cdot 10^{-123}}$

Виртуальная масса центрального тела

Сверхмалое значение виртуальной массы планеты должно компенсироваться большим значением «виртуальной массы» центрального тела ${displaystyle M_{x}}$ . Это значение может быть найдено следующим образом. Рассмотрим силу Ньютона для реальных масс:

${displaystyle F_{NR}={frac {mM}{4pi epsilon _{G}r^{2}}} }$

А также силу Ньютона для виртуальных масс в виде:

${displaystyle F_{NR}={frac {(h/m_{x})(h/M_{x})}{4pi mu _{G}r^{2}}} }$

Далее используя равенство этих сил:

${displaystyle F_{NR}=F_{NR} }$

можно найти виртуальную массу центрального тела:

${displaystyle M_{x}=4beta _{N}^{2}cdot {frac {m_{N}^{4}}{m_{x}mM}}=1.2424cdot 10^{37} }$

кг,

в случае Солнечной системы, где ${displaystyle beta _{N}=1/4alpha _{N}=1.427116cdot 10^{44} }$ .
Таким образом, отсутствие корректного введения «гравитационных монополей» приводит к спекуляциям различного рода, как в области паранауки (различные «торсионные поля»), так в области подлинной науки (введение т.н. «темной материи») и т.д.

Смотри также

Квантовый гравитационный резонатор

Ссылки

↑ Symposium on the origin of the Solar System. (1972) Raris, Edition du Centre National de la Recherche Scientifique.
↑ Caldirola P, Pavisic M and Recami E, Nuov.Cim. 48B (1978) 205.
↑ Sivaram C and Sinha KP, Phys.Reports 51 (1979) 111.
↑ L. Nottale, G. Schumacher and J. Gay, A&A, 332 (1997) 1018.
↑ Godel K, Rev.Mod.Phys. 21 (1949) 447.
↑ A. Rubcic and J. Rubcic, Fizika B 4 (1995) 11
↑ A. Rubcic and J. Rubcic, Fizika B 7 (1998) 1
↑ A. Rubcic and J. Rubcic, Fizika B 5 (1996) 85
↑ ^9,0 ^9,1 ANTUN RUBCIC and JASNA RUBCIC. SQUARE LAW FOR ORBITS IN EXTRA-SOLAR PLANETARY SYSTEMS.Quantization in Astrophysics, Brownian Motion, and Supersymmetry. Editors: F.Smarandache and V.Christanto. MathTiger, 2007, Chennai, Tamil Nadu, India. ISBN: 819021909X.
↑ Saulo Carneiro (1997). The Large Numbers Hypothesis and Quantum Mechanics. arxiv:gr-qc/9712014v1
↑ M. Oliveira Neto and L.A. Maia, Advances in Space Dynamics, A. F. Bertachini, Editor, pp 456-470 (2000).
↑ Marcal de Oliveira Neto, Liliane de Almeida Maia, Saulo Carneiro. A DESCRIPTION OF EXTRA-SOLAR PLANETARY ORBITS THROUGH A SCHRODINGER – TYPE DIFFUSION EQUATION. ADVANCES IN SPACE DYNAMICS 4: CELESTIAL MECHANICS AND ASTRONAUTICS, H. K. Kuga, Editor, 113-121 (2004).
↑ A. G. Agnese and R. Festa, Phys. Lett. A, 227 (1997) 165.
↑ Allen C.W.(1973). Astrophysical quantities. 3-d edition. University of London, The Athlone Press.

Литература

Quantization in Astrophysics, Brownian Motion, and Supersymmetry. Editors: F.Smarandache and V.Christanto. MathTiger, 2007, Chennai, Tamil Nadu, India. ISBN: 819021909X.
Д.тер Хаар. Некоторые замечания о теориях происхождения Солнечной системы из первичной солнечной туманности. с.107.
С.Ф.Дермонт. Закон Боде и преобладание приблизительной соизмеримости среди пар орбитальных периодов в Солнечной системе. с. 466.
Происхождение солнечной системыю Под реакцией Г.Ривса.М.:Мир,1976. 570с.

Источник

где T1 и T2 — периоды обращения двух планет вокруг Солнца,
a1 и a2 — длины больших полуосей их орбит.

Если орбита следующей планеты в 2 раза дальше предыдущей (т.е., a₂ = 2 a₁),
то период её орбиты будет примерно в 3 раза больше:

T₂ = T₁ × √(2³/1) = T₁ × √8 ≈ 2,828 T₁ ≅ 3T₁.

§ 4.4. Орбитальные резонансы планет СС

Орбита следующей планеты с учетом поправки Ньютона: T₂ = √8 × T₁ (M + m₁) / (M + m₂).
Т.е., если следующая планета меньше предыдущей, то ее резонанс лучше приблизится к 3:1,
если больше — то сдвинется к 2,5 и может стать 5:2.
Поэтому реально резонансы могут быть разные (табл. 2).

№	Планета	Расчётное расстояние, а.е.	Истинное расстояние, а.е.	Кратность осей	Период, зем.лет	Период, мерк.лет	Период в ΔT_{Вен-Мерк}	Другие резонансы
1	Меркурий	0,4	0,387	—	0,24	1	—	1/4 Зем, 2/5 Вен
2	Венера	0,7	0,723	1,5-2 Мер (1,85)	0,62	≅ 3 [?]	1 (0,38 з.л.)	~2/3 или 3/5 Зем
3	Земля	1,0	1,000	2,5 Мер	1,0	~4	1 (0,38 з.л.)	5/3 Вен
4	Марс	1,6	1,523	~2 Вен	1,88	~8	2,3 (0,88 з.л.)	3 Вен, ~2 Зем
5	Астероиды	2,8	2,20-3,65	2 Мар, 3 Зем, 3-5 (≅4) Вен, 7 Мер	4,6	19 (~20)	7,1 (2,7 з.л.)	7 Вен, ≅ 2 Мар
6	Юпитер	5,2	5,202	≅ 2 Аст, ≅ 7/2 или 10/3 Мар, 7 Вен	11, 9	50	19,2 (7,3 з.л.)	5/2 Аст, 6 Мар, 12 Зем, 19 Вен
7	Сатурн	10,0	9,538	2 Юп	29,5	123 (~120)	46,3 (17,6 з.л.)	5/2 Юп, 30 Зем, ≅ 40 Вен
8	Уран	19,6	19,182	2 Сат, ≅ 7 Аст	84,0	350	143,4 (54,5 з.л.)	≅ 3 Сат, 7 Юп
9	Нептун	38,8	30,058	3 Сат, 6 Юп, ≅ 10 Аст	164,8	687 (~700)	212,6 (80,8 з.л.)	2 Ур, 14 Юп
10	Плутон	77,2	39,44	2 Ур	248,5	1035 (~1050)	220,3 (83,7 з.л.)	3/2 Неп, 3 Ур, 8 Сат, 21 Юп

Табл. 2. Периоды обращения планет СА и их резонансы.

Наиболее простыми резонансами являются ¹/₂, ³/₂, ⁵/₂;
¹/₃, ²/₃; ³/₄; ²/₅,
³/₅; ³/₇, ⁴/7.

Положим их в последовательный ряд:
0,3 (1/3), 0,4 (2/5 и 3/7), 0,5 (1/2), 0,6 (3/5 и 4/7), 0,7 (2/3), 0,8 (3/4);
1,5 (3/2); 2,5 (5/2).
Как видим, здесь находится место Меркурию, ВЫенере, Марсу, Фаэтону (астероидам).

Ряд этот получается слишком плотным — вероятно, из этих исключаются из-за гравитационного напряжения между объектами орбит.
Полностью заполнится он может только для малых тел.

§ 4.5. Орбитальные правила для планет земной группы

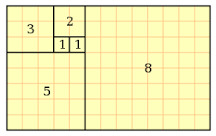
Квадраты Золотого сечения со сторонами из ряда Фибоначчи (геометрическое представление чисел Фидия)

Гармонию и внутреннюю устойчивость характеризует ряд Фибоначчи [Владимирский 2013],
который строится путём сложения соседних двух чисел, если ряд начать с двух единиц:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…

Если в этом ряду делить число на предыдущее, то результат будет стремиться к 1,618.
Это число называется Золотым сечением или числом Фидия (и числом Фибоначчи тоже называют).

Число Фидия можно также вычислить по упрощенной формуле:
Ф = (1 + √ 5) / 2 [Урманцев 2013, с. 19].

Рис. 1. Золотое сечение.

Расположим в ряд расстояния от Солнца до планет, выраженные в астрономических единицах:

0,39; 0,72; 1,0; 1,52; 2,8 (расчётное); 5,20; 9,54; 19,18; 30,06; 39,44 …

Умножим его на 5: 1,95; 3,6; 5; 7,6; 14; 26; 47,7; 95,9;150,3; 197,2.

Мы видим убедительное сходство, особенно для планет земной группы, относящихся к внутренней орбитальной зоне.

Получается, если орбиты планет-гигантов расположены друг к другу по удвоенным расстояниям
(к Нептуну раньше это тоже могло относится), то орбиты земных планет раскладываются в ряд Фибоначчи.
Правило же Тициуса-Боде вмещает в себя обе эти закономерности.

§ 4.6. Орбитальные пробелы в астероидах и кольцах Сатурна

Большую серию резонансных движений, воспринимаемых опять-таки как досадные помехи в стройной теории,
доставляет пояс астероидов [Ипатов 2010, Молчанов 1974].
Хорошо известны щели (пробелы, люки) Кирквуда [Резонансы 2006, с.с. 9, 53],
соответствующие резонансам 2:5, 1:3 с обращением Юпитера.
Менее заметные понижения в кривой распределения периодов обращения астероидов возникают при резонансах 1:4, 1:5, 3:5, 3:7.

Существует и противоположная ситуация – группировка орбит вблизи точек 3:4 и 2:3.

В музыкальной терминологии это «кварта» и «квинта». «Прима» также устойчива и соответствует группе троянцев.

Знаменитая «щель Кассини» в Кольцах Сатурна имеет резонансную природу.
Она занимает ту зону, в которой частички, составляющие кольца Сатурна, имели бы периоды,
близкие к 1/2 периода Мимаса, 1/3 периода Энцелада и1/4 периода Тефии.

Для понимания этого явления недостаточно было обнаружить щель и открыть спутники Сатурна.
С этим справился сам Кассини. Мало было даже открыть другие пробелы в кольцах Сатурна.
Только в ХIХ веке Кирквуд, сопоставив пробелы в поясе астероидов с кольцами Сатурна,
осознал единый резонансный Механизм образования пробелов.

§ 4.7. Орбитальные правила для транснептунов

Начиная с 30 а.е. (орбита Нептуна) начинается пояс Койпера
[Витязев, с. 2; Кусков и др. 2009, с. 37], который продолжается примерно до 55 а.е. от Солнца.
К этой области принадлежит карликовая планета Плутон.

На самой орбите Плутона находятся резонансные ему плутино, чьи 3 оборота равны 4 оборотам Нептуна ~220 лет.

Далее открытые малые планеты располагаются «слоями» (возможно, не все еще открыты,
возможно, имеют место щели и пробелы, как в астероидах и кольцах Сатурна,
под влиянием неких более массивных космических тел).

От 40 до 60 а.е. (период обращения 250-290 лет) малые планеты идут сплошным массивом.

Следующий слой уже закойперовских планет
начинается с 80 а.е., потом – примерно со 100 а.е. (орбитальный период от 500 лет).

Заслуживает внимание резонанс 3-х малых планет, имеющих резонанс 1:2:4:

Плутоид Варуна, или 2000 WR106 — 43 а.е., 282 г.
Трансплутон Эрида (также Ксена, Зена, или 2003 UB313 — 97 а.е., 560 лет.
Объект 2014 UZ224 — примерно 155 а.е., 1136 лет.

В этой связи уместно опять вспомнить правило Тициуса-Боде и продолжить наш список «законных» орбит СС:
40, 80, 160, 320, 640, 1280…
Дальше продолжать не имеет смысла, ибо любая планета, расположенная далее 600 а.е., должна сойти со своей орбиты.
И мы видим, что упомянутые 3 резонансные планеты как раз лежат на расчетных орбитах 40, 80 и 160.
А самой дальней извесной планетой за поясом Койпера является Седна, находящаяся в 500 а.е. от Солнца,
не считая некой «планеты X», открытой на кончике пера, и находящейся, действительно,
на самом краю СС – в 600 а.е. или даже дальше, которая уже вписывается в классическую расчетную орбиту 640 а.е.

§ 4.8. Особенности орбит спутников планет-гигантов

Системы спутников планет-гигантов [Астрономия 2009, с. 568]
имеют общую структуру — они состоят из 3 зон:

внутренней, где расположены спутники существенно меньшего размера (часто — астероиды), чем в центральной зоне;
центральной, где представлены «классические» спутники с устоявшимися круговыми орбитами;
внешней, где находятся, в основном, астероиды, случайно захваченные планетой (яркий пример — Феба —
самая дальняя из известных сатурнианских лун) [Симоненко 1985, с. 79].

Нас сначала будут интересовать закономерности орбит спутников центральной зоны. И здесь можно увидеть 2 подтипа:

примерно одинаковые по размерам и плотности спутники, как галилеевские спутники Юпитера или классические спутники Сатурна
и спутники меньшего размера, но с одним самым крупным, как Титан на Сатурне или Титания на Уране, Тритон на Нептуне.

Последний случай напоминает планеты Солнечной системы,так же состоящие из 3 зон и очень крупным Юпитером в центральной зоне.
Посмотрим, как будут соответствовать закономерности орбит спутников в этих 2-х подтипах.

Особенности орбит спутников Юпитера

Орбитальные характеристики спутников Юпитера
(центральные, или «галилеевские», выделены розовым) — см. табл. 3:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Юпитера
Метида	128	0,3	(40)
Адрастея	129	0,3	(25)
Амальтея	181	0,5 ~ 3/2 = 5/3 T_Адр	195*
Теба	221	0,7 ~ 3/2 T_Ама	(80)
II. Центральные («галилеевские») спутники Юпитера
Ио	422	1,8 = 5/2 T_Теб	3640
Европа	671	3,6 = 2 T_Ио	3130
Ганимед	1070 = 1,5 R_Ев	7,2 = 2 T_Евр	5280
Каллисто	1883	16,7 ~ 5/2 T_Ган	4850
III. Ближние внешние спутники Юпитера
Леда	11094	239 ~ 14 T_Кал	(15)
Гималия	11480	251	170
Лиситея	11720	259	(20)
Элара	11737	260	80
IIV. Дальние внешние спутники Юпитера
Ананке	21200	631	(20)
Карме	22600	692	(30)
Пасифе	23500	735	(40)
Синопе	23700	758	(30)

Табл. 3. Периоды обращения юпитерианских спутников.

Видим, что первые 3 галилеевских спутника имеют радиусы орбит примерно в 1,5 (точнее — в 1,59) раз больше предыдущего
и периоды в 2 раза больше, чем у предыдущего спутника.

Это можно выразить формулой [Мюррей 2010, с. 30; Сурдин 2009, с. 62]:
1/T_Ио — 3/T_Евр + 2/T_Ган = 0.

Особенности орбит спутников Сатурна

Орбитальные характеристики спутников Сатурна
(центральные, или «классические», выделены розовым) — см. табл. 4:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Сатурна
Пан	134	0,6	(20)
Атлант	138	0,6	(30)
Прометей	139	0,6	(110)
Пандора	142	0,6	(100)
Эпиметей	151	0,7	(130)
Янус	151	0,7	190
II. Центральные спутники Сатурна
Мимас	186	0,9	390
Энцелад	238	1,4	500
Тефия	295	1,9	1060
Телесто	295	1,9	(30)
Калипсо	295	1,9	(30)
Диона	377	2,7	1120
Елена	377	2,7	(35)
Рея	527	4,5	1530
Титан	1222	15,9	5150
Гиперион	1481	21,3	300
Япет	3561	79,3	1460
III. Внешние спутники Сатурна
Феба	12952	550,5	(220)

Табл. 4. Периоды обращения сатурнианских спутников.

Особенности орбит спутников Урана

Орбитальные характеристики спутников Урана — см. табл. 5:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Урана
Корделия	50	0,3	(25)
Офелия	54	0,4	(30)
Бианка	59	0,4	(40)
Крессида	62	0,5	(60)
Дездемона	63	0,5	(50)
Джульетта	64	0,5	(80)
Порция	66	0,5	(110)
Розалинда	70	0,5	(50)
Белинда	75	0,6	(70)
Пэк	86	0,8	(150)
II. Центральные спутники Урана
Миранда	129	1,4	480
Ариэль	191	2,5	1160
Умбриэль	266	4,1	1170
Титания	436	8,7	1580
Оберон	584	13,5	1520
III. Внешние спутники Урана
Калибан	7169	580	(60)
Сикоракса	12214	1290	(120)

Табл. 5. Периоды обращения уранианских спутников.

Особенности орбит спутников Нептуна

Орбитальные характеристики спутников Нептуна — см. табл. 6:

Название спутника	Радиус орбиты, тыс. км	Период обращения, сут.	Диаметр, км	Масса, млн.т.	Эксцен- триситет	Наклон орбиты, °
I. Внутренние спутники Нептуна
Наяда	48	0,3	(50)
Таласса	50	0,3	(80)
Деспина	53	0,3	(150)
Галатея	62	0,4	(160)
Ларисса	74	0,6	(200)
II. Центральные спутники Нептуна
Протей	118	1,1	420
Тритон	355	5,9	2700
III. Внешние спутники Нептуна
Нереида	5513	360,2	340

Табл. 6. Периоды обращения нептуновых спутников.

Что забавно, периоды Галатеи, Лариссы, Протея и Тритона соотносятся как расстояния в а.е.
от Солнца до Меркурия, Венеры, Земли и Юпитера (см. табл. 1, 2).

§ 4.9. Орбитальные правила расположения экзопланет

Примерно треть открытых экзопланет входит в мультипланетные системы,
которых известно уже более 130. Наличие орбитальных резонансов там широко распространено.

Известные системы
с резонансом 2:1 — Gliese 876 и HD 82943, с резонансом 3:1 — 55 Cnc.
У Gliese 876 резонансы как у галилеевских спутников Юпитера: 4:2:1 («резонанс Лапласа»).
А недавно открыта плотно упакованная планетами резонансная система Kepler 223,
у которой такой резонансный ряд еще длиннее: 8:4:2:1 [Маров 2017, с. 63].

В Галактике у большинства звезд с экзопланетами самые массивные из них расположены не на наибольшем удалении от светил,
а рядом с ними (ближе, чем Меркурий к Солнцу) — там находятся горячие экзопланеты с небольшими периодами вращения.

В феврале 2017 года была открыта экзопланетная система TRAPPIST-1.
Вокруг красного карлика обращается 7 планет, 6 из которых находятся в цепочке резонансов 2:3:4:6:9:15:24.

Видно, что здесь средний множитель для следующей орбиты — 1,5, — как в земной группе.
Возможно, это особенность всех близких орбит.

Далее, по аналогии, в этой звёздной системе могут быть планеты с резонансами 36:54.

5. Природа явления

Перейдём от астрономических исследований (того, что видим) к физическим (того, что не видим).
Попытаемся установить:
1) законы формирования резонансной конфигурации в мультиорбитальной системе;
2) физический смысл правила Тициуса-Боде (если он есть),
уточнив его и выразив через переменные.

§ 5.1. Кратности и разности в резонансах

§ 5.2. Суммарные гравитационные потенциалы на орбитах

§ 5.3. Физический смысл закона Тициуса-Боде и его уточнение

6. Применение полученных знаний

§ 6.1. Вычисение «на кончике пера» новых орбит

На основании правил распределения транснептуновых планет (см. § 4.7)
и уточненного закона Тициуса-Боде (см. § 5.3) для них
можно предположить наиболее вероятные орбиты пока не найденных новых планет Солнечной системы.

§ 6.2. Восстановление предыдущих конфигураций орбит

На основании правила Тициуса-Боде пока весьма осторожно можно высказаться о том,
что Нептун был на средней орбите Плутона (40 а.е.).
Видимо, именно Нептун сформировал пояс Койпера.
Сам Плутон, возможно, был спутником Нептуна.

Сами спутники Нептуна, вероятно, принадлежали поясу Койпера.
Это можно эскизно исследовать по их плотностям.

Причиной орбитальной перестройки мог быть массивное космическое тело (транзитная
экзопланета или планета-гигант пролетающей мимо звезды
из ближайшего окружения Солнца),
проходившая перпендикулярно плоскости эклиптики.

Например, звезда Шольца, которая сейчас отстоит на 20 световых лет,
50 тысяч лет назад приблизилась к Солнечной системе
и даже пересекла Облако Оорта (кометный резервуар).
В это время ее расстояние до центра Солнца было 0,8 световых лет
(52 000 а.е. или 8 трлн км) — это в 5 раз ближе, чем нынешняя ближайшая звезда
Проксима Центавра.

В более далёкие времена это могли быть другие звёзды.

Это космическое событие могло быть причиной и поворота Урана по оси на 90°.

§ 6.3. Предсказание перестройки орбитальных систем

§ 6.4. Влияние конфигураций планет на Солнце и Землю

7. Заключение

В данном исследовании получены следующие результаты:

Орбиты планет СС делятся на 3 зоны (земные, гиганты, койперовские), для расстояний в которых разные правила.
Орбиты планет земного типа (до Юпитера) выстраиваются в ряд Фибоначчи.
Планеты-гиганты имеют 2-кратную дальность относительно предыдущей.
При этом их резонансные характеристики близки к 3:1.
Транснептуновые планеты «лежат слоями» через 20 а.е.
Правило Тициуса-Боде (ПТБ) хорошо описывает орбиты первых 2-х групп.
В целом, оно является правилом удвоения, только для первых планет применяется множитель не 2,
а число Фидия (1,618), характеризующее Золотое сечение.
Исключение составляют Нептун и Плутон, но эти исключения лишь подтверждают правило,
т.к. Нептун был на орбите нынешнего Плутона , который был его спутником.
Орбиты спутников планет-гигантов также делятся на 3 зоны:
внутренние астероиды, срединные классические, внешние астероиды.
Орбиты в первой и последней группах могут иметь незакономерный характер
(и сами эти астероиды имеют сильный эксцентриситет и могут иметь большой наклон к орбите других спутников).
У классических спутников можно найти свои правила расположения.

8. Глоссарий

Некоторые термины и аббревиатуры, встречающиеся в статье:

ПГ — планеты-гиганты (Юпитер, Сатурн, Уран, Нептун).
ПЗГ — планеты земной группы (Меркурий, Венера, Земля, Марс).
СА — солнечная активность, определяемая количеством солнечных пятен (индексируемых числом Вольфа).

9. Литература

Астрономия: век XXI. /
Ред.-сост. Сурдин В.Г. – Фрязино: «Век 2», 2008. – 2-е изд., испр. и доп. – 608 с.: ил.
[Есть в Озоне.]
Витязев А.В., Печерникова Г.В.
Происхождение малых тел Солнечной системы. — 5 с. Статья подарена автором в виде распечатки.
Владимирский Б.М.
Солнечная активность и общественная жизнь.
Космическая историометрия: от первых российских космистов до наших дней. — М.: Кн.дом «ЛИБРОКОМ», 2013. – 192 с.
[Есть в URSS.]
Гаршин И.К. Космический ритм экологических кризисов и дальних миграций кочевников Евразии. //
Материалы
выездной сессию 11-й Крымской конференции «Космос и биосферы» в Санкт-Петербурге
в рамках 7-го конгресса «Слабые и сверхслабые поля и излучения в биологии и медицине» (7–11 сентября 2015);
Симпозиум B. «Слабые воздействия на организменном и популяционном уровне и устойчивость жизненных процессов в биосфере.
Экологические и социальные последствия слабых воздействий», С. 133.
Ипатов С.И. Миграция небесных тел в Солнечной системе. — М.: Физматлит, 2010. – 320 с.
[Есть в Озоне.]
Кусков О.Л., Дорофеева В.А., Кронрод В.А., Макалкин А.Б.
Системы Юпитера и Сатурна: Формирование, состав и внутреннее строение крупных спутников /
Отв. ред. М.Я. Маров. — М.: Изд. ЛКИ, 2009. — 576 с.
Маров М.Я., Шевченко И.И.
Экзопланеты. Экзопланетология. — М.-Ижевск: Институт компьютерных исследований, 2017. — 138 с.
Молчанов А.М.
Гипотеза резонансной структуры Солнечной системы. — Препринт. Пущино: НЦБИАН СССР, 1974. — 19 с.
Мюррей К., Дермотт С. Динамика Солнечной системы. /
Пер. с англ. под ред. И.И. Шевченко. — М.: Физматлит, 2010. — 588 с.
Резонансы в небесной механике / Сб. работ. —
Москва-Ижевск: Ин-т компьютерных исследований, 2006. — 316 с.
Симоненко А.Н. Гипотеза резонансной структуры Солнечной системы.
— М.: Наука, Гл. ред. физ.-мат. лит-ры. — 1985. — 208 с.
Солнечная система. / Ред.-сост. Сурдин В.Г. —
М.: ФИЗМАТЛИТ, 2009. — 400 с. — (Астрономия и астрофизика).
Урманцев Ю.А. Симметрия природы и природа симметрии.
Философские и естественно-научные аспекты. Изд. 4-е. — М.: Книжный дом «ЛИБРОКОМ», 2013. — 232 с.

10. Благодарности

Сердечное спасибо оргкомитету международной крымской конференции «Космос и биосфера»
за разрешение выступить с докладом, ставшим анонсом этой статьи.
И особо я признателен председателю оргкомитета Владимирскому Борису Михайловичу
за библиографическую помощь и научные советы.

11. Дополнительные сведения о статье

Доклад по данной теме впервые был зачитан в октябре 2017 года
на XII Международном конгрессе «Космос и биосфера» в Алуште (Крым).

На правах рекламы (см.
условия):

Ключевые слова для поиска сведений по гравитационным орбитальным закономерностям:

На русском языке: закономерности планетарных орбит, регулярности гравитационного обращения, орбитальные законы Кеплера,
правило Тициуса-Боде, движение планет и спутников, гравитационно-орбитальные резонансы, орбитально-гравитационное квантование;

На английском языке: Planetar orbital regularities.

Страница обновлена 15.03.2022

Источник