Как найти радиус основы конуса

Как найти радиус основания конуса

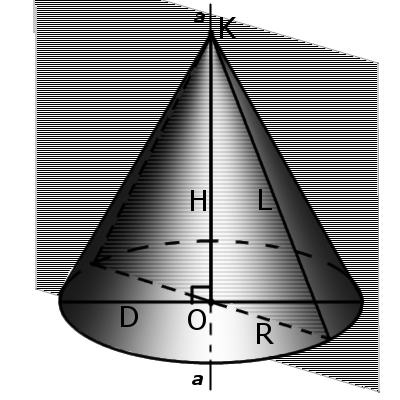
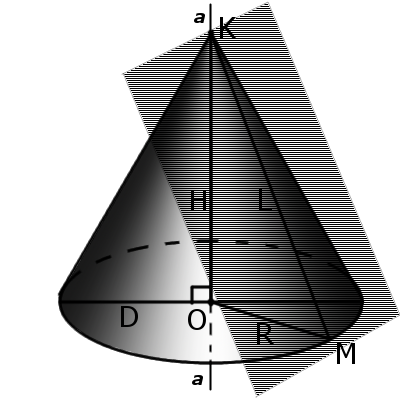
Прямой конус — это тело, которое получается при вращении прямоугольного треугольника вокруг одного из катетов. Этот катет есть высота конуса H, другой катет является радиусом его основания R, гипотенуза равна множеству образующих конуса L. Способ нахождения радиуса конуса зависит от исходных данных задачи.

Инструкция

Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3∙πR²H. Получите: R²=3V/πH, откуда R=√(3V/πH).

Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=πRL. Вы получите R=S/πL.

Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L²=R²+H². Выразите из данной формулы R, получите: R²=L²–H² и R=√(L²–H²).

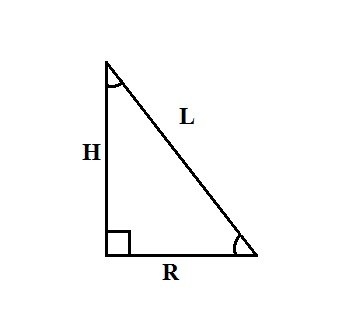
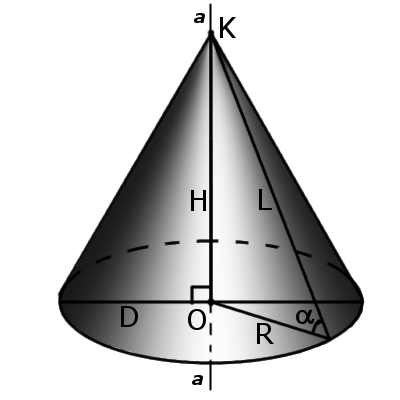
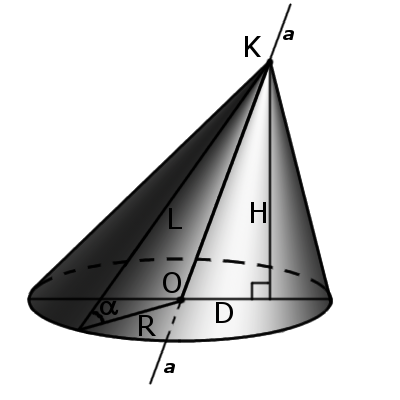
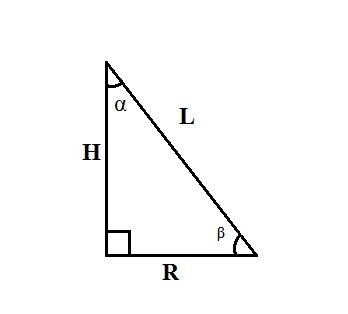
Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если известны образующая конуса L и угол α между высотой конуса и его образующей, найдите радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L∙sinα.

Если известны образующая конуса L и угол β между радиусом основания конуса и его образующей, найдите радиус основания R по формуле: R=L∙cosβ. Если известны высота конуса H и угол α между его образующей и радиусом основания, найдите радиус основания R по формуле: R=H∙tgα.

Пример: образующая конуса L равна 20 см и угол α между образующей и высотой конуса равен 15º. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом α противолежащий этому углу катет R вычисляется по формуле R=L∙sinα. Подставьте соответствующие значения, получите: R=L∙sinα=20∙sin15º. Sin15º находится из формул тригонометрических функций половинного аргумента и равен 0,5√(2–√3). Отсюда катет R=20∙0,5√(2–√3)=10√(2–√3)см. Соответственно, радиус основания конуса R равен 10√(2–√3)см.

Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30º, равен половине гипотенузы. Таким образом, если известны длина образующей конуса и угол между его образующей и высотой равен 30º, то найдите радиус по формуле: R=1/2L.

Связанная статья

Можно ли линейку принять за материальную точку

Источники:

• Решение треугольников
• радиусы образуют прямой угол

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как обнаружить радиус основания конуса

Прямой конус – это тело, которое получается при вращении прямоугольного треугольника вокруг одного из катетов. Данный катет есть высота конуса H, иной катет является радиусом его основания R, гипотенуза равна множеству образующих конуса L. Метод нахождения радиуса конуса зависит от начальных данных задачи.

Инструкция

1. Если вам знамениты объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3??R?H. Получите: R?=3V/?H, откуда R=?(3V/?H).

2. Если вам вестимы площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=?RL. Вы получите R=S/?L.

3. Следующие методы нахождения радиуса основания конуса основываются на заявлении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам вестимы высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L?=R?+H?. Выразите из данной формулы R, получите: R?=L?–H? и R=?(L?–H?).

4. Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если знамениты образующая конуса L и угол ? между высотой конуса и его образующей, обнаружьте радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L?sin?.

5. Если знамениты образующая конуса L и угол ? между радиусом основания конуса и его образующей, обнаружьте радиус основания R по формуле: R=L?cos?. Если знамениты высота конуса H и угол ? между его образующей и радиусом основания, обнаружьте радиус основания R по формуле: R=H?tg?.

6. Пример: образующая конуса L равна 20 см и угол ? между образующей и высотой конуса равен 15?. Обнаружьте радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом ? противолежащий этому углу катет R вычисляется по формуле R=L?sin?. Подставьте соответствующие значения, получите: R=L?sin?=20?sin15?. Sin15? находится из формул тригонометрических функций половинного довода и равен 0,5?(2–?3). Отсель катет R=20?0,5?(2–?3)=10?(2–?3)см. Соответственно, радиус основания конуса R равен 10?(2–?3)см.

7. Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30?, равен половине гипотенузы. Таким образом, если знамениты длина образующей конуса и угол между его образующей и высотой равен 30?, то обнаружьте радиус по формуле: R=1/2L.

Элементы конуса

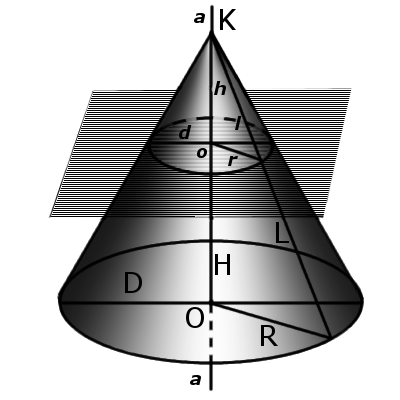
Определение. Вершина конуса — это точка (K), из которой исходят лучи.

Определение. Основание конуса — это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.

Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.

Определение. Направляющая конуса — это кривая, которая описывает контур основания конуса.

Определение. Боковая поверхность конуса — это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.

Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.

Определение. Высота конуса (H) — это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.

Определение. Ось конуса (a) — это прямая, проходящая через вершину конуса и центр основания конуса.

Уравнение конуса

Основные свойства кругового конуса

Как вычислить радиус окружности конуса

Радиус и высота конуса

Свойства

Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания. d=2r P=2πr S_(осн.)=πr^2

Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2) l=√(h^2+r^2 ) tan⁡β=h/r α=180°-2β

Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора. S_(б.п.)=πrl=πr√(h^2+r^2 ) S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)

Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три. V=1/3 S_(осн.) h=(πr^2 h)/3

Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4) r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r) R=(h^2+r^2)/2h

Калькулятор расчета радиуса описанной около конуса сферы (шара)

В публикации представлены онлайн-калькуляторы и формулы для расчета радиуса описанной около конуса сферы (шара) по двум группам исходных данных: через радиус основания фигуры и длину ее образующей (или высоту).

Расчет радиуса сферы (шара)

Инструкция по использованию: введите радиус основания конуса (R), длину его образующей (l) или высоту (h=BE), затем нажмите кнопку “Рассчитать”. В результате будет вычислен радиус (r) сферы (шара), описанной вокруг конуса.

Формулы для вычисления диаметра конуса. Пример решения геометрической задачи

Фигура конус является объектом изучения стереометрии. Основными свойствами конуса являются наличие у него объема и площади поверхности, которые можно вычислить с помощью линейных параметров. Одним из них является диаметр конуса. В данной статье покажем, как этот диаметр можно рассчитать по другим известным характеристикам фигуры.

Круглый прямой конус

В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая — директрисой, или направляющей.

Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.

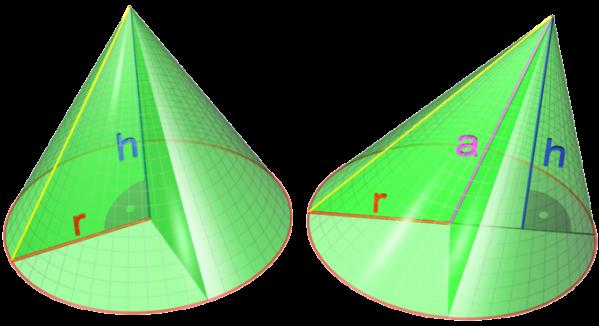
Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.

Здесь r — радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.

Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая — это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.

Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.

Вычисление диаметра фигуры через линейные параметры и угол при основании

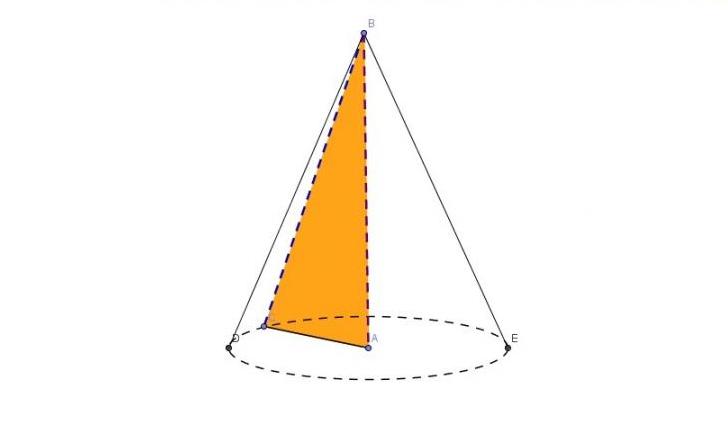
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.

Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:

При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.

Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:

Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.

Вычисление диаметра через площадь поверхности и генератрису

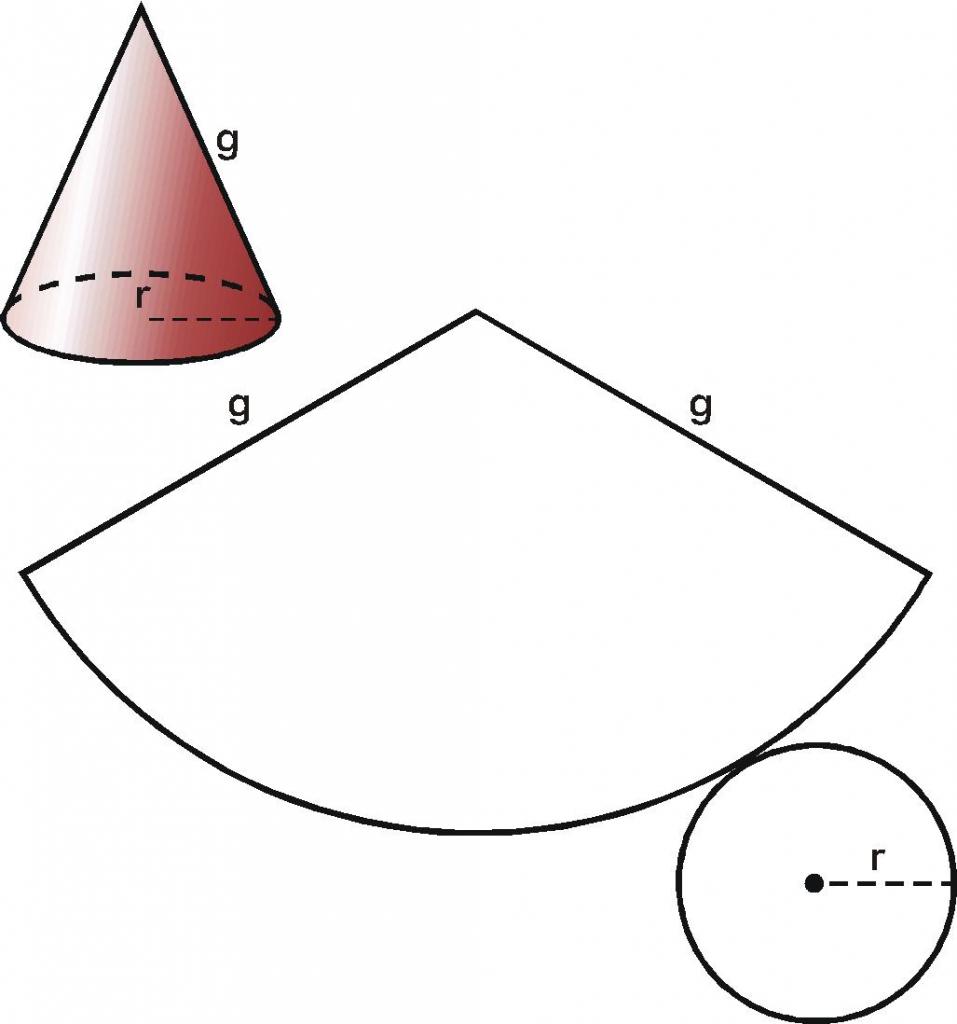
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.

Общая площадь развертки определяется по следующей формуле:

Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.

С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.

Определение диаметра через объем и высоту

Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:

Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:

Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:

Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.

Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r — 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Радиус и образующая конуса

Свойства

Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2

Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cos⁡β=r/l α=180°-2β

Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)

Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3

Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h

Как определить радиус окружности основания конуса

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a ), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б ), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в ), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г ), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д ). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.

 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.

Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = АВ • РC. Имеем: ОР = R (по условию); в △ A OB : ОС = ; в △ ОСР : CP = = .

Тогда S △ ABP = АВ • РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

S бок = α • l 2 , (1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

S кон = π Rl + π R 2 . (3)

Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому

S бок = 2 π ВС • AD. (4)

Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем

= ⇒ BC • AD = DE • АС. (5)

Тогда соотношение (4) принимает вид

S бок = (2 π • DE ) • AC, (6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F 1 , при этом центр О основания отображается на центр О 1 круга F 1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X 1 = РX ∩ α . Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

= = k, (*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

S сечен : S основ = k 2 = : PO 2 .

18.7. Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

— прямоугольный треугольник (см. рис. 179);

План изучения темы

1. Понятие конуса.
2. Площадь поверхности конуса.
3. Объём конуса.
4. Усечённый конус.
5. Площадь поверхности усечённого конуса.
6. Объём усечённого конуса.
7. Решение задач на тему «Конус».

Понятие конуса

Точка Р — вершина конуса. РО — ось конуса, а её отрезок, заключенный между вершиной и основанием — высота конуса. Основание конуса — это круг, на который опирается данная геометрическая фигура. Любая прямая, соединяющая вершину Р с точкой на окружности основания (РА, РВ) — это образующая конуса (обозначается l). Поверхность, составленная их образующих — это боковая поверхность конуса.

Площадь поверхности конуса

Как и цилиндр, конус имеет два вида площадей — площадь боковой поверхности и площадь полной поверхности.

Развёртка конуса представляет собой сектор. Отсюда есть разные формулы нахождения площади боковой поверхности.

Это формула при использовании развёртки, как сектора. Если же учесть, что длина дуги сектора равна длине окружности основания конуса, то получаем равенство:

где r — радиус основания конуса. Тогда имеем вторую, более простую формулу нахождения площади боковой поверхности конуса:

Площадь полной поверхности состоит из боковой и основания конуса. Значит, формула нахождения этой площади:

Объём конуса

где r — радиус основания конуса, h — высота конуса.

Усечённый конус

Если на какой-либо высоте конуса провести секущую плоскость, параллельную основанию, то мы получим две фигуры: конус меньшего объёма сверху и усечённый конус внизу. При этом, составляющие элементы будут как у обычного конуса: образующие, ось, высота, боковая поверхность. Отличие — будет уже два основания, которые отличаются по площади.

Площадь поверхности усечённого конуса

Из-за того, что теперь у нас два основания, формула площади боковой поверхности усеченного конуса будет выглядеть иначе:

Само собой, меняется и формула площади полной поверхности:

Объём усечённого конуса

Решение задач на тему «Конус»

Пример 1 (Ященко 36 вариантов, 2021 год, вариант 7)

В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 высоты. Объём жидкости составляет 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд.

Решение: объём конуса вычисляется по формуле:

Высота налитой жидкости 0,25 от всей высоты конуса. Значит, высота в 4 раза больше. Но при этом, не забывайте, что радиус всего конуса тоже увеличится в 4 раза. Так как мы на осевом сечении получаем случай подобных треугольников:

С учётом таких изменений, наш новый объём (объём всего конуса) примет вид:

Видим, что объём всего конуса в 64 раза больше налитой жидкости. Значит, в миллилитрах это будет:

Получается, что долить нужно 315 миллилитров.

Ответ: 315

Пример 2 (Ященко 36 вариантов, 2021 год, вариант 11)

Цилиндр и конус имеют общее основание и высоту. Объём цилиндра равен 162. Найдите объём конуса.

Решение: формулы объёмов цилиндра и конуса отличаются незначительно.

Видим, что отличие только в дроби 1/3 в формуле объёма конуса. А раз по условию высота и основания совпадают, значит объём конуса будет просто в 3 раза меньше. Значит, он равен 54.

Ответ: 54

Пример 3 (Ященко 36 вариантов, 2021 год, вариант 25)

Площадь боковой поверхности конуса равна 30. Параллельно основанию конуса проведено сечение, делящее его высоту в отношении 2:3, считая от вершины конуса. Найдите площадь боковой поверхности отсечённого конуса.

Решение: разберемся для начала, какие подобные треугольники тут можно получить.

Видим, что треугольник SAD подобен треугольнику SBC с коэффициентом подобия 2/5. Значит, площади боковых поверхностей конуса и отсечённого конуса будут иметь отношение подобия в квадрате (из-за того, что это площади, а не длины каких-то сторон).

Отсечённый конус — это тот, что сверху, маленький. Значит, с учётом коэффициента подобия:

Ответ: 4,8