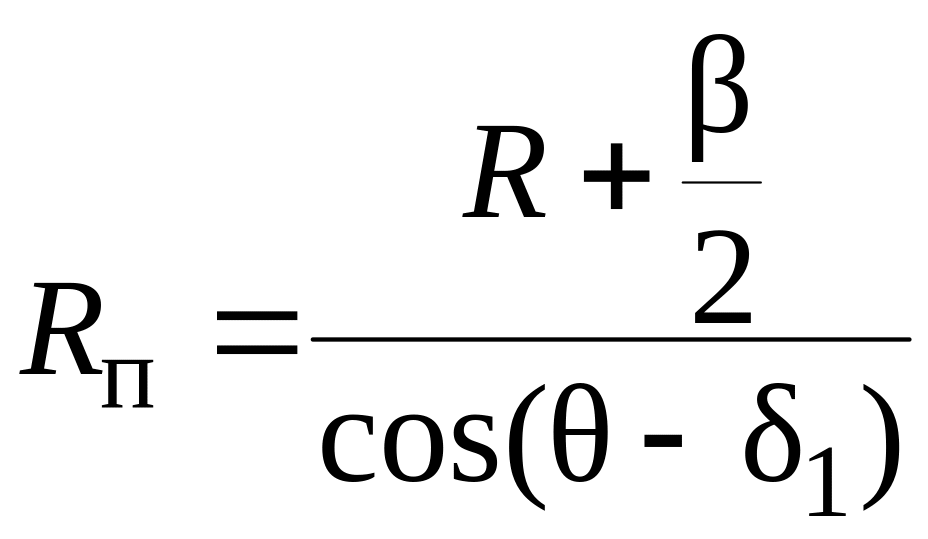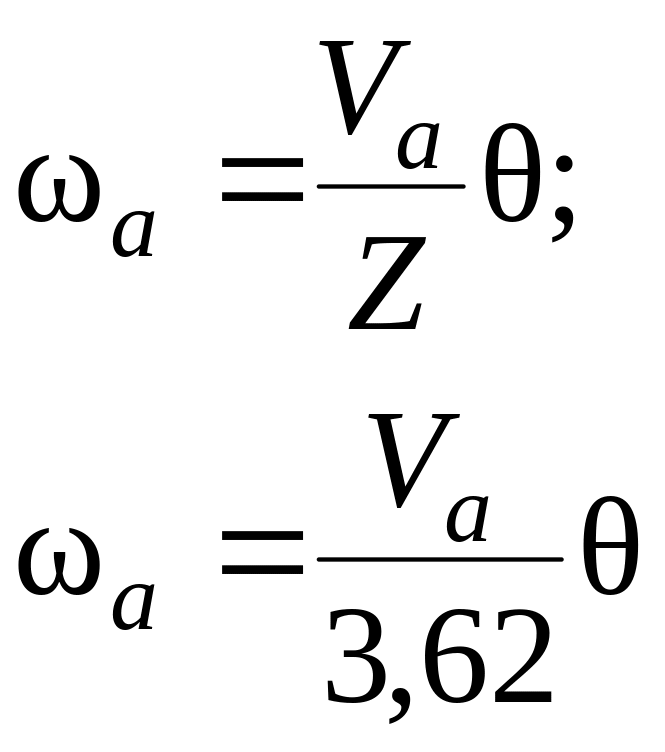Как найти радиус поворота формула

Enter the wheelbase length and the turning angle of the front wheels into the calculator to determine the turning radius.

• Wheel Speed Calculator
• Piston Speed Calculator (mean)
• HP to Torque Calculator
• CC to HP Calculator
• GVWR (Gross Vehicle Weight Rating) Calculator
• Trailer Tongue Length Calculator
• Handwheel Diameter Calculator
• Aircraft Turn Radius Calculator
• MPH to G Force Calculator

Turning Radius Formula

The following formula is used to calculate the turning radius of a car.

TR = WB/tan(a)

• Where TR is the turning radius
• a is the angle of the turn
• WB is the wheelbase (distance between centers of the front and back wheels)

This formula assumes a perfect theoretical turning scenario. In real-world situations, this turning radius would vary depending on wheel tilt, friction, and many other factors.

Turning Radius Definition

What is a turning radius? A turning radius is a radius at which a car will rotate, or turn, given a certain wheelbase length and an angle of turn of the wheels.

Example Problem

FAQ

What is a good turning radius?

Most common cars have a turning radius of 35′ so anything smaller than that would be considered good. This is the turning radius of the car assuming the wheels are turned as much as possible.

Do bigger tires affect the turning radius?

Typically larger wheels will increase the turning radius of a vehicle to more wheel tilt during turning.

Is a smaller or larger turning radius better?

A smaller turning radius is better for handling and cars that want to perform well on a track will want to try to decrease the turning radius as much as possible.

What is the turning radius?

The turning radius is the minimum radius of the path that a vehicle must follow in order to make a turn without skidding or losing control. It is defined as the distance from the center of the turning circle to the center of the vehicle.

How is turning radius calculated?

The turning radius can be calculated by dividing the wheelbase of the vehicle (the distance between the front and rear axles) by the tangent of the angle of the turn. The formula is: R = (WB) / tan (Θ), where R is the turning radius, WB is the wheelbase, and Θ is the angle of the turn.

What is the relationship between speed and turning radius?

The relationship between speed and turning radius is inversely proportional, meaning that as speed increases, the turning radius decreases. This is because at higher speeds, the vehicle must follow a tighter turning radius in order to maintain stability and control.

Why is turning radius important in vehicle design?

Turning radius is an important factor in vehicle design because it affects the maneuverability of the vehicle. A smaller turning radius allows a vehicle to make tighter turns, which can be useful in tight spaces, while a larger turning radius can make it more difficult to maneuver in tight spaces.

How does the weight of a vehicle affect its turning radius?

The weight of a vehicle affects its turning radius by increasing the forces acting on the tires during a turn. As a result, a heavier vehicle will require a larger turning radius in order to maintain stability and control.

How does the width of a vehicle affect its turning radius?

The width of a vehicle affects its turning radius by increasing the distance between the tires, which increases the forces acting on the tires during a turn. As a result, a wider vehicle will require a larger turning radius in order to maintain stability and control.

What is the relationship between tire size and turning radius?

The relationship between tire size and turning radius is indirect. Larger tires can increase the stability of a vehicle during a turn, but they also increase the distance between the tires, which can result in a larger turning radius.

How does the suspension of a vehicle affect its turning radius?

The suspension of a vehicle affects its turning radius by changing the way the vehicle handles during a turn. A softer suspension can increase the stability of the vehicle during a turn, but can also increase the turning radius. A stiffer suspension can reduce the turning radius, but can also decrease the stability of the vehicle during a turn.

How does the type of vehicle affect its turning radius?

The type of vehicle can greatly affect its turning radius. For example, larger vehicles like buses and trucks typically have a larger turning radius than smaller vehicles like cars, due to their increased length and width.

How is turning radius measured?

Turning radius can be measured by observing the path that a vehicle follows during a turn and measuring the distance from the center of the turning circle to the center of the vehicle. This measurement can be made using a variety of tools, including laser measuring devices or tape measures.

---

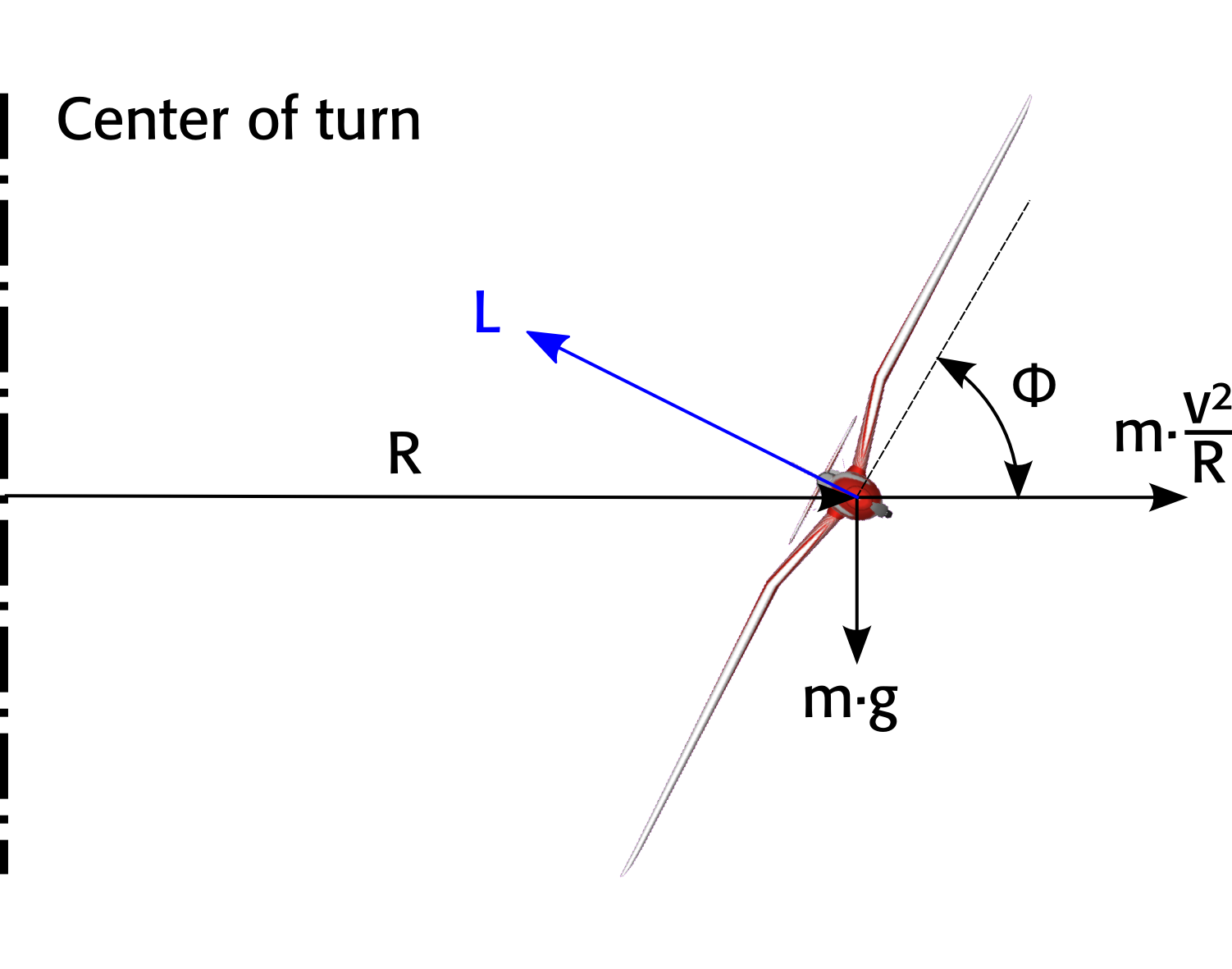
После всех этих ответов с имперскими единицами позвольте мне объяснить это с единицами Си, начиная с первых принципов. R-радиус, v-скорость полета, m-масса,g — гравитационная постоянная, Φ — угол крена и L-подъем.

Подъем должен быть равен весу (m·g) и центробежной силе (m·ω2·R = m·v2R

v2R

), так

L = (m ⋅ g ) 2 + (m ω ω 2 ⋅ R ) − − − − − − − − − − − − − − − √ = ρ 2 ⋅ v 2 ⋅ c L ⋅ S
L=(m⋅g)2+(m⋅ω2⋅R)=ρ2⋅v2⋅cL⋅S

с ρ плотность воздуха, cL

cL

коэффициент подъемной силы и S площадь поверхности крыла. Теперь конвертируйте, чтобы вы получили v:

v = (m ⋅ g ) 2 (ρ 2 ⋅ c L ⋅ S ) 2 — (m R ) 2 − − − − − − − − − − − − − − − √ 4
v=(m⋅g)2(ρ2⋅cL⋅S)2−(mR)24

Теперь вы можете видеть, что номинатор не может стать нулевым или меньше, что дает вам минимальный радиус для заданной скорости и максимального коэффициента подъема c L m A x

cLmax

:

R ≥ 2 ⋅ m ρ 2 ⋅ c L m A x ⋅ S,
R≥2⋅mρ2⋅cLmax⋅S,

и вообще:

R = 2 ⋅ m ρ 2 ⋅ c L ⋅ S = v ω = v 2 g ⋅ n 2 z− 1 − − − − − √
R=2⋅mρ2⋅cL⋅S=vω=v2g⋅nz2−1

Это похоже на «радиусный барьер»: повороты не могут лететь плотнее, чем это. Это происходит из-за увеличения центробежной силы, которая прибывает из более крутых поворотов полета. Чем круче поворот, тем быстрее вы должны лететь, чтобы создать достаточный подъем для компенсации веса и центробежной силы.

Что все еще увеличивается, так это ваша угловая скорость ω:

ω = v R = g ⋅ t A n Φ v = g ⋅ n 2 z− 1 − − − − − √ v
ω=vR=g⋅tanΦv=g⋅nz2−1v

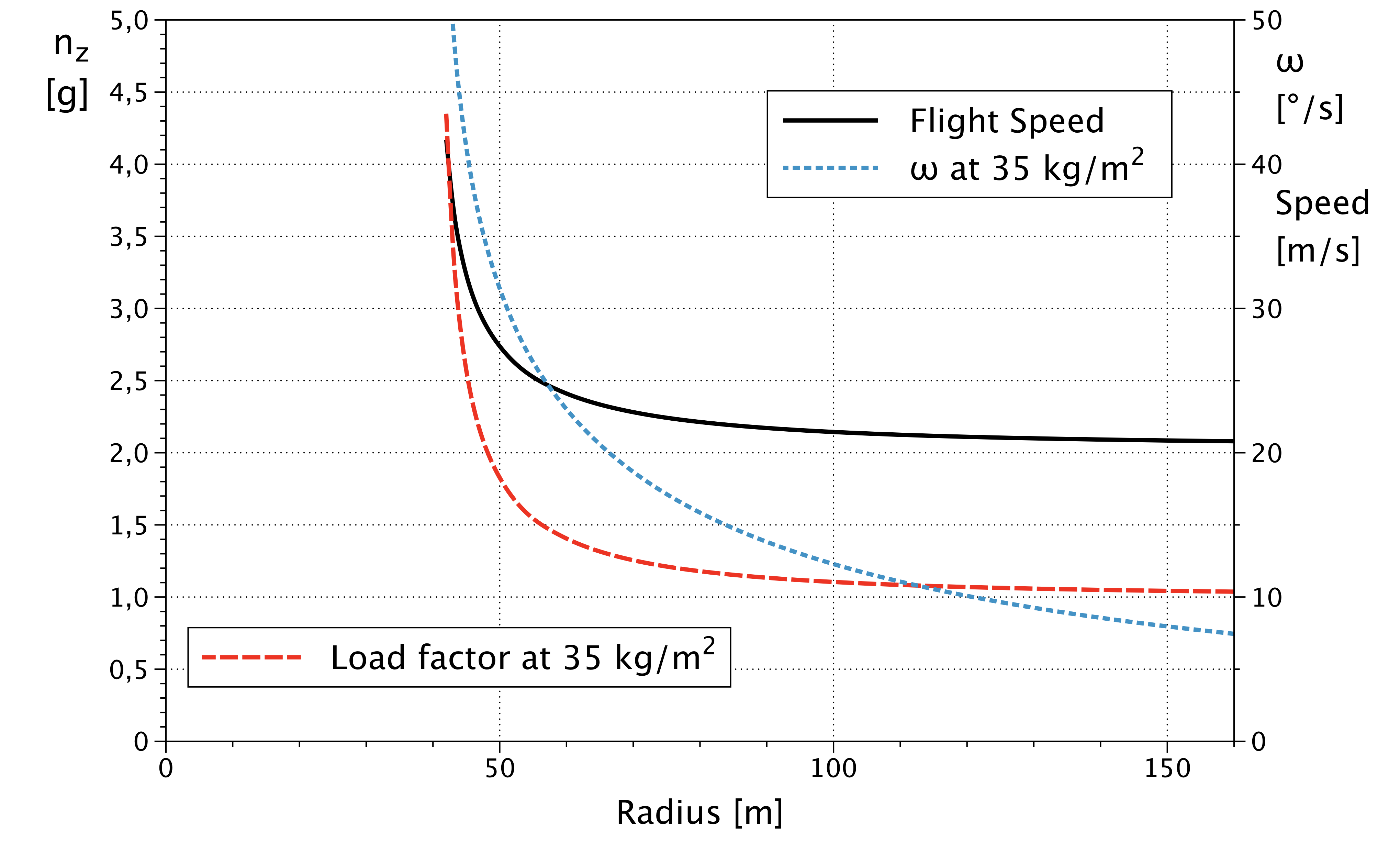
Внизу я построил планер. Вы можете ясно видеть радиус барьера на 40 м. Поверьте мне, это выглядит точно так же для авиалайнера, только цифры больше.

Если вам нужна быстрая формула для оценки радиуса, вам нужно использовать квадрат воздушной скорости, так что это не простая линейная зависимость. Для поворота с креном 30° (nz

nz

= 1.15), знаменатель уравнения радиуса составляет около 4, поэтому, чтобы вычислить радиус поворота в метрах, разделите квадрат воздушной скорости на 4 или возьмите квадрат половины вашей воздушной скорости в метрах в секунду.

Для скорости поворота в градусах в секунду разделите 220 на скорость полета в метрах в секунду. Полет медленнее позволяет более высокую скорость поворота.

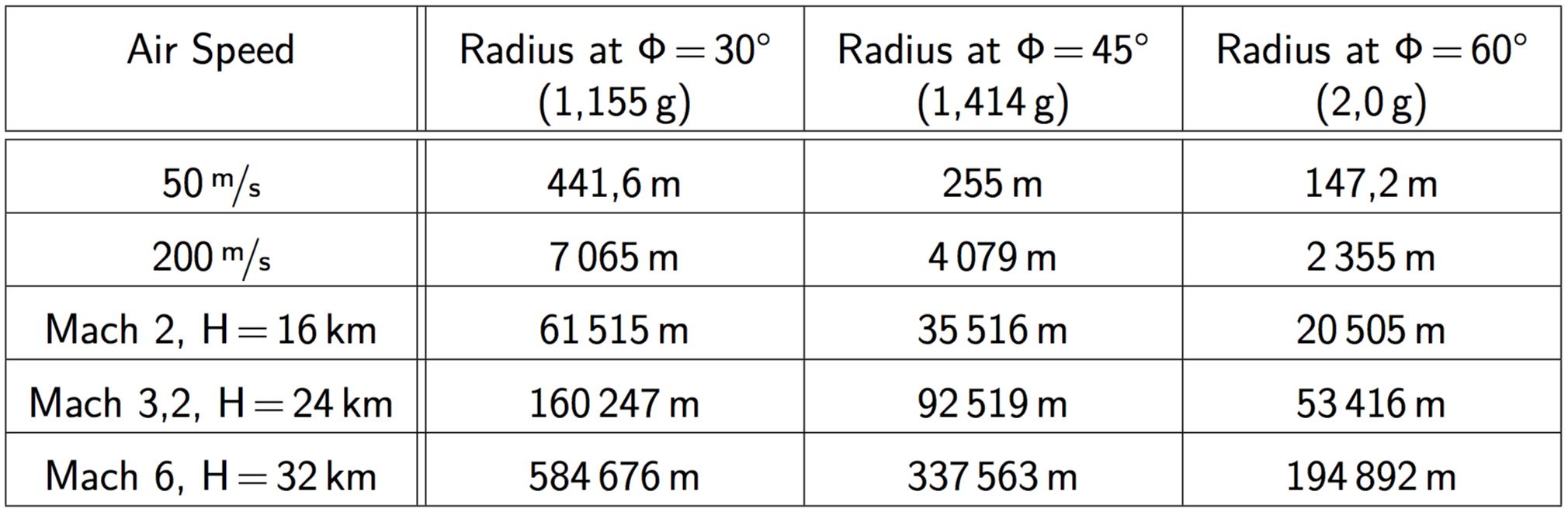
Теперь о другой крайности: гиперзвуковым самолетам нужно много места для маневрирования. У меня есть здесь некоторые ценности, просто для удовольствия:

Высокая скорость делает это почти терпимым, в конце концов, половина оборота на Mach 6 и 2 g занимает всего 336 секунд, то есть менее 6 минут. Авиалайнеры крен только 30° или меньше, поэтому первая колонка действительна, если вы летите ваш гиперзвуковой автомобиль, как авиалайнер.

Коэффициент трения
между дорогой и автомобилем равен 0,10. Найти наименьший радиус поворота,
который может сделать автомобиль, движущийся со скоростью 36 км/ч.

Решение.

Автомобиль можно
рассматривать как материальную точку, которая движется по окружности радиусом R со скоростью v. Следовательно,
автомобиль движется с центростремительным ускорением a.
На него действуют сила тяги F, сила тяжести mg, сила нормальной реакции опоры N,
сила сопротивления движению F_с и сила трения покой F_тр .

В направлении ускорения
на автомобиль действует единственная сила – сила трения покоя F_тр­ . Второй закон Ньютона
в проекциях на ось x: ma = F_тр .

Следует обратить
внимание на то, что рассматриваемая сила трения – эта сила трения покоя. Если
бы она отсутствовала, но присутствовала только сила трения скольжения, то
автомобиль не смог бы двигаться по окружности, поскольку он должен был бы
скользить в радиальном направлении. Только в этом случае возникла бы сила
трения, направленная к оси вращения и обеспечивающая центростремительное
ускорение автомобиля. Тогда автомобиль двигался бы по раскручивающейся спирали.
Это означает, что под коэффициентом трения в условии задачи следует понимать
коэффициент трения покой. Следовательно, F_тр =  m₀N.

Кроме того, на автомобиль
действуют сила трения качения и сила сопротивления воздуха. Они представлены в
виде результирующей силы – силы F_с . Она направлена по касательной к окружности, по которой
движется автомобиль. Поэтому эта сила не связана с центростремительным
ускорением автомобиля. Она преодолевается силой тяги.

На рассматриваемую
систему действуют еще две силы: сила тяжести и сила нормальной реакции опоры.
Обе эти силы действуют в вертикальном направлении. Поскольку ускорение
автомобиля в вертикальном направлении равно нулю, что векторная сумма этих сил
равна нулю. Следовательно, по модулю N =  mg. Поскольку a = v²/R, из предыдущих формул
имеем: mv²/R = m₀mg. Отсюда R = v²/m₀g. Подставляя численные
значения, найдем R = 100 м = 0,1 км.

Ответ: R =0,1 км.

Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.

Радиус поборота и угловая скорость поворота

При
изучении кинематики поворота автомобиля
его рассматривают как твердое тело.
Мгновенный центр поворота твердого
тела можно найти, если известно направление
скоростей двух любых его точек.
Воспользуемся этим положением для
нахождения мгновенного центра поворота
автомобиля.

Будем
считать, что мы знаем направление
скоростейV_а
и V_б
точек А и Б, являющихся серединами
соответственно задней и передней осей
автомобиля (рис. 43).

Направление
скоростей V_а
и V_б
зависит
от направления скоростей колес
соответствующих осей. Если бы колеса
были жесткими, то скорости обоих колес
задней оси располагались в плоскостях
их качения, параллельных продольной
оси автомобиля. В этом случае направление
скорости V_a
совпадало
бы с продольной осью автомобиля.Из-за
явления увода, вызванного наличием
боковых сил, всегда действующих на
колеса при повороте автомобиля,
направления скоростей колес отклоняются
от плоскостей их качения. В связи с этим
и направление скорости V_a
располагается
относительно продольной оси автомобиля
под некоторым углом δ₂,
который будем называть углом увода
задней оси.

Поскольку
передние колеса автомобиля для его
поворота устанавливаются под некоторым
углом к продольной оси, то даже при
жестких колесах вектор скорости точки
Б будет располагаться под некоторым
углом θ к продольной оси автомобиля.
Если бы оба колеса поворачивались на
одинаковый угол, то угол θ был бы равен
углу поворота колес. Однако из-за того,
что колеса связаны между собой рулевой
трапецией, они поворачиваются на разные
углы.
Можно
доказать, что

,
где θ_в
и θ_н
– углы поворота колес соответственного
внутреннего и наружного по отношению
к центру поворота.

Рис.
43. Схема увода автомобиля

Из-за
увода передних колес, вызванного
действующими на них боковыми силами,
вектор скорости V_Б
отклоняется
от того направления, которое имела бы
скорость точки Б при жестких колесах
на некоторый угол δ₁
(угол
увода передней оси).Угол между вектором
V_Б
и
продольной осью автомобиля с учетом
увода равен θ – δ₁
.

Для
определения положения мгновенного
центра поворота автомобиля восстановим
в точках А и Б перпендикуляры к направлениям
скоростей V_А
и V_Б.

Точка
пересечения этих перпендикуляров и
будет мгновенным центром поворота 0_п
автомобиля. Будем определять положение
этой точки расстояниями R
до
продольной оси автомобиля и С до его
задней оси.

Опустим
из центра поворота перпендикуляр 0_пB
на продольную ось автомобиля.

AB
= С = R
tg
δ₂;
(135)

ВБ
= R
tg
(θ – δ₁);
(136)

Складывая
(135) и (136), получим

;
(137)

Радиусом
R_п
поворота
автомобиля называют расстояние от
центра поворота 0_п
до колеи переднего наружного колеса
(рис.43):

;
(138)

При
достаточно больших R
(и, следовательно, не очень больших θ)
можно пренебречь величиной B/2
по
сравнению с R
и считать сos(θ-δ₁)
равным
единице, тогда R_п
≈ R.

В
дальнейшем, если это не оговорено особо,
будем пренебрегать разницей между R
и R_п,
называя R
радиусом поворота.

Зная
расстояние от центра поворота до
продольной оси автомобиля, можно найти
угловую скорость поворота автомобиля.
Угловая скорость w_a
автомобиля
равна скорости V_B
точки
В продольной оси автомобиля, выраженной
в м/с, деленной на R:

Поскольку
О_пВ
перпендикуляр к продольной оси, то
скорость V_В
направлена
по продольной оси автомобиля и,
следовательно, является скоростью
автомобиля, тогда если

в м/с, то

;
(139)

Если
уводом колес можно пренебрегать, считая
колеса жесткими, то, пользуясь уравнениями
(135), (136), получим:

R
= Z/tgθ
≈ z/θ;
C=0
(140)

Следовательно,
при отсутствии увода центр поворота
всегда лежит на продолжении осей задних
колес автомобиля. Из уравнений (137), (138)
в этом случае

Rп
= z/sinθ
+ B/2cosθ
≈ Z/sinθ
(141)

Наконец,
пользуясь уравнением (139), получим:

;
(142)

где

—
скорость автомобиля, км/ч.

Из
сравнения формул, определявших R
и ω_a
без
учета и с учетом увода, видно, что в
первом случае как радиус поворота, так
и угловая скорость однозначно определяются
углом поворота управляемых колес, а во
втором при одном и том же угле поворота
управляемых колес могут быть различными
в зависимости от разности углов увода
δ₂
–
δ₁.

Если
δ₂
– δ₁
=
0, то радиус поворота и угловая скорость
автомобиля так же, как и у автомобиля с
жесткими колесами, зависит только от
угла поворота θ.

Такой
случай движения называют нейтральной
поворачиваемостью автомобиля.

Хотя
при нейтральной поворачиваемости радиус
поворота и угловая скорость с учетом
увода такие же, как у автомобиля с
жесткими колесами, траектории движения
автомобиля различны, поскольку, как
видно из равенства (137), при δ₂
≠
0;
С ≠
0
и,
следовательно, центр поворота с учетом
увода и в этом случае не лежит на
продолжении осей задних колес, т.е. не
совпадает с центром поворота автомобиля
с жесткими колесами.

Если
δ₂
–
δ₁
>
0,
то
радиус поворота с учетом увода при
одинаковых θ меньше радиуса поворота
автомобиля с жесткими колесами, а угловая
скорость с учетом увода больше, чем у
автомобиля с жесткими колесами.

Такой
случай движения называют недостаточной
поворачиваемостью.

Поворачиваемость
автомобиля зависит как от характера
движения (вход в поворот, выход из
поворота, круговое движение и др.), так
и от конструктивных особенностей
автомобиля.Автомобили, у которых при
круговом движении имеет место нейтральная,
избыточная или недостаточная
поворачиваемость, называют автомобилями
соответственно с
нейтральной, избыточной и недостаточной
поворачиваемостью.

Поворачиваемость
автомобиля зависит как от характера
движения (вход в поворот, выход из
поворота, круговое движение, движение
на повороте с ускорением или замедлением
и т. д.), так и от конструктивных особенностей
автомобиля. Автомобили, у которых при
круговом движении имеет место та или
другая поворачиваемость, называются
соответственно автомобили с нейтральной,
избыточной или недостаточной
поворачиваемостью.Для предотвращения
получения избыточной поворачиваемости,
что опасно, т. к. автомобиль автоматически
входит в «спираль» на повороте, на всех
автомобилях делают недостаточную
поворачиваемость. Это достигается
увеличение давления в шинах задних
колес при одинаковой нагрузке на колеса
передней и задней осей, установкой
сдвоенных шин, или одновременно тем и
другим, или уменьшением нагрузки на
заднюю ось при одинаковом давлении
воздуха в шинах.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить