Как найти радиус проводящей сферы - Исправление недочетов и поиск решений вместе с Examum.ru

Тема: Определить радиус проводящей сферы, если её потенциал равен (Прочитано 7573 раз)

0 Пользователей и 1 Гость просматривают эту тему.

kirill5555

Определить в см радиус проводящей сферы, если при сообщении ей заряда в 20 нКл её потенциал стал равен 6 кВ.

« Последнее редактирование: 25 Февраля 2012, 08:45 от alsak »

Записан

Kivir

Решение: потенциал проводящей сферы (шара) рассчитывается по формуле:

[ varphi =frac{kcdot q}{R}, ]

Здесь k =1/4πε₀ = 9∙10⁹ Н∙м²/ Кл² – коэффициент пропорциональности, q — заряд сферы, R – радиус. Выражаем искомый радиус:

[ R=frac{kcdot q}{varphi }. ]

Ответ: 3 см.

Записан

Источник

Download Article

The radius of a sphere (abbreviated as the variable r or R) is the distance from the exact center of the sphere to a point on the outside edge of that sphere. As with circles, the radius of a sphere is often an essential piece of starting information for calculating the shape’s diameter, circumference, surface area, and/or volume. However, you can also work backward from the diameter, circumference, etc. to find the sphere’s radius. Use the formula that works with the information you have.

1
Find the radius if you know the diameter. The radius is half the diameter, so use the formula r = D/2. This is identical to the method used for calculating the radius of a circle from its diameter.^[1]
- If you have a sphere with a diameter of 16 cm, find the radius by dividing 16/2 to get 8 cm. If the diameter is 42, then the radius is 21.
2
Find the radius if you know the circumference. Use the formula C/2π. Since the circumference is equal to πD, which is equal to 2πr, dividing the circumference by 2π will give the radius.^[2]
- If you have a sphere with a circumference of 20 m, find the radius by dividing 20/2π = 3.183 m.
- Use the same formula to convert between the radius and circumference of a circle.
Advertisement
3
Calculate the radius if you know the volume of a sphere. Use the formula ((V/π)(3/4))^1/3.^[3] The volume of a sphere is derived from the equation V = (4/3)πr³. Solving for the r variable in this equation gets ((V/π)(3/4))^1/3 = r, meaning that the radius of a sphere is equal to the volume divided by π, times 3/4, all taken to the 1/3 power (or the cube root.)^[4]
- If you have a sphere with a volume of 100 inches³, solve for the radius as follows:
  - ((V/π)(3/4))^1/3 = r
  - ((100/π)(3/4))^1/3 = r
  - ((31.83)(3/4))^1/3 = r
  - (23.87)^1/3 = r
  - 2.88 in = r
4
Find the radius from the surface area. Use the formula r = √(A/(4π)). The surface area of a sphere is derived from the equation A = 4πr². Solving for the r variable yields √(A/(4π)) = r, meaning that the radius of a sphere is equal to the square root of the surface area divided by 4π. You can also take (A/(4π)) to the 1/2 power for the same result.^[5]
- If you have a sphere with a surface area of 1,200 cm², solve for the radius as follows:
  - √(A/(4π)) = r
  - √(1200/(4π)) = r
  - √(300/(π)) = r
  - √(95.49) = r
  - 9.77 cm = r

1
Identify the basic measurements of a sphere. The radius (r) is the distance from the exact center of the sphere to any point on the surface of the sphere. Generally speaking, you can find the radius of a sphere if you know the diameter, the circumference, the volume, or the surface area.
- Diameter (D): the distance across the sphere – double the radius. Diameter is the length of a line through the center of the sphere: from one point on the outside of the sphere to a corresponding point directly across from it. In other words, the greatest possible distance between two points on the sphere.
- Circumference (C): the one-dimensional distance around the sphere at its widest point. In other words, the perimeter of a spherical cross-section whose plane passes through the center of the sphere.
- Volume (V): the three-dimensional space contained inside the sphere. It is the «space that the sphere takes up.»^[6]
- Surface Area (A): the two-dimensional area on the outside surface of the sphere. The amount of flat space that covers the outside of the sphere.
- Pi (π): a constant that expresses the ratio of the circle’s circumference to the circle’s diameter. The first ten digits of Pi are always 3.141592653, although it is usually rounded to 3.14.
2
Use various measurements to find the radius. You can use the diameter, circumference, volume, and surface area to calculate the radius of a sphere. You can also calculate each of these numbers if you know the length of the radius itself. Thus, to find the radius, try reversing the formulas for these components’ calculations. Learn the formulas that use the radius to find diameter, circumference, volume, and surface area.^[7]
- D = 2r. As with circles, the diameter of a sphere is twice the radius.
- C = πD or 2πr. As with circles, the circumference of a sphere is equal to π times the diameter. Since the diameter is twice the radius, we can also say that the circumference is twice the radius times π.
- V = (4/3)πr³. The volume of a sphere is the radius cubed (times itself twice), times π, times 4/3.
- A = 4πr². The surface area of a sphere is the radius squared (times itself), times π, times 4. Since the area of a circle is πr², it can also be said that the surface area of a sphere is four times the area of the circle formed by its circumference.

1
Find the (x,y,z) coordinates of the central point of the sphere. One way to think of the radius of a sphere is as the distance between the point at the center of the sphere and any point on the surface of the sphere. Because this is true, if you know the coordinates of the point at the center of the sphere and of any point on the surface, you can find the radius of the sphere simply by calculating the distance between the two points with a variant of the basic distance formula. To begin, find the coordinates of the sphere’s center point. Note that because spheres are three-dimensional, this will be an (x,y,z) point rather than an (x,y) point.
- This process is easier to understand by following along with an example. For our purposes, let’s say that we have a sphere centered around the (x,y,z) point (4, -1, 12). In the next few steps, we’ll use this point to help find the radius.
2
Find the coordinates of a point on the surface of the sphere. Next, you’ll need to find the (x,y,z) coordinates of a point on the surface of the sphere. This can be any point on the surface of the sphere. Because the points on the surface of a sphere are equidistant from the center point by definition, any point will work for determining the radius.
- For our example problem, let’s say that we know that the point (3, 3, 0) lies on the surface of the sphere. By calculating the distance between this point and the center point, we can find the radius.
3
Find the radius with the formula d = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²).^[8] Now that you know the center of the sphere and a point on the surface, calculating the distance between the two will find the radius. Use the three-dimensional distance formula d = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²), where d equals distance, (x₁,y₁,z₁) equals the coordinates of the center point, and (x₂,y₂,z₂) equals the coordinates of the point on the surface to find the distance between the two points.
- In our example, we would plug in (4, -1, 12) for (x₁,y₁,z₁) and (3, 3, 0) for (x₂,y₂,z₂), solving as follows:
  - d = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²)
  - d = √((3 — 4)² + (3 — -1)² + (0 — 12)²)
  - d = √((-1)² + (4)² + (-12)²)
  - d = √(1 + 16 + 144)
  - d = √(161)
  - d = 12.69. This is the radius of our sphere.
4
Know that, in general cases, r = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²).^[9] In a sphere, every point on the surface of the sphere is the same distance from the center point. If we take the three-dimensional distance formula above and replace the «d» variable with the «r» variable for radius, we get a form of the equation that can can find the radius given any center point (x₁,y₁,z₁) and any corresponding surface point (x₂,y₂,z₂).
- By squaring both sides of this equation, we get r² = (x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)². Note that this is essentially equal to the basic sphere equation r² = x² + y² + z² which assumes a center point of (0,0,0).

Add New Question

Question

How do I find the radius of a sphere if I know its volume is three times its surface area?

Write an equation whereby the volume [(4πr³) / 3] is set equal to three times the surface area (4πr²). Thus, [(4πr³) / 3] = 12πr². Divide both sides by 4π, so that r³/3 = r². Multiply by 3: r³ = 3r². Divide by r²: r = 3. In other words, a sphere’s volume can be three times its surface area only if its radius is 3 units.
Question

How do I calculate the radius of a sphere in my hand by using a ruler?

You can get a very close approximation by carefully measuring the circumference and dividing by twice-pi (6.28).
Question

Two solid spheres A & B are made of the same material. The radius of B is 3 times the radius of A, and the surface area of A is 20 cubic cm. How do I calculate the surface area of B?

The surface area (S) of a sphere equals 4πr², where r is the radius. Using that equation to solve for r: r = √(S / 4π). Now substitute 20 for S, and solve for the radius of sphere A: r = √(20 / 4π) = √(20 / 12.56) = √ 1.59 = 1.26 cm. That’s the radius of sphere A. The radius of sphere B is three times the radius of sphere A: (3)(1.26) = 3.79 cm. So for sphere B, the surface area is 4πr² = (4)(3.14)(3.79)² = 180.4 square centimeters. (That answer makes sense, because when you multiply the radius of a sphere by 3, you multiply its surface area by 3² or 9.) (We didn’t exactly triple the original surface area, because we rounded off some numbers along the way.)

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

This article was published on demand. However, if you are trying to get to grips with solid geometry for the first time, it’s arguably better to start the other end: calculating the properties of the sphere from the radius.
The order in which the operations are performed matters. If you are uncertain how priorities work, and your calculating device supports parentheses, then make sure to use them.
π or pi is a Greek letter that represents the ratio of the diameter of a circle to its circumference. It’s an irrational number and cannot be written as a ratio of 2 integers. Many approximations exist, 333/106 gives pi to four decimal places. Today most people memorize the approximation 3.14 which is usually sufficiently accurate for everyday purposes.

Show More Tips

Thanks for submitting a tip for review!

About This Article

Article SummaryX

If you know the diameter, you can find the radius of a sphere by dividing the diameter in half. If you know the circumference, you can find the radius by dividing the circumference by 2 times pi. To learn how to calculate the radius of a sphere using two points on the sphere, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 522,422 times.

Did this article help you?

Источник

Перед тем, как смело броситься на амбразуру решения задачи по нахождению радиуса сферы, нужно узнать, что вообще такое сфера и шар. Стереометрия говорит нам, что сфера – это поверхность, состоящая из массы точек пространства, которые находятся на одном расстоянии от центра. Эта точка – центр сферы, а радиус сферы (R) – это расстояние, на которое каждая точка удалена от центра сферы. Шар – это тело, которое ограничено поверхностью сферы.

Безусловно, способ определения того самого радиуса сферы будет зависеть от данных, которые у нас есть.

Способ 1. Определение радиуса сферы при помощи площади ее поверхности

Допустим, нам дана сфера вместе с площадью её поверхности. В таком случае мы будем использовать формулу площади её поверхности для того, чтобы вычислить радиус.

где S – это площадь поверхности сферы, число Пи = 3,14.

Способ 2. Определение радиуса сферы при помощи объема шара

Если нам дан объём шара, ограниченного сферой, то радиус находится так:

где V — это объём шара, число Пи = 3,14.

Способ 3. Альтернативные формулы определения радиуса сферы

В случае, если наша сфера вписана в правильный многогранник или описана вокруг него, можно воспользоваться следующим рядом формул.

Формула 1. Сфера вписана в правильный тетраэдр

Для сферы, которая вписана в правильный тетраэдр:

где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).

Формула 2. Сфера описана около правильного тетраэдра

Для сферы, которая описана около правильного тетраэдра:

где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).

Формула 3. Сфера вписана в куб

Для сферы, которая вписана в куб:

где a – длина ребра куба.

Формула 4. Сфера описана около куба

Для сферы, которая описана около куба:

где a – длина ребра куба.

Источник

Примеры решения задач по физике — концентрические проводящие сферы

Суббота, 25 февраля, 2012

Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.

Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.

Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φ_in (внутренней) и φ_ex (внешней).

Решение. Потенциал на поверхности внутренней сферы φ_exскладывается из двух потенциалов: внешней сферы φ₁ и собственно внутренней сферы φ₂.

Потенциал внешней сферы φ₁ в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):

$[ varphi_1 = frac{Q}{4pivarepsilon_0 R}. ]$

Потенциал внутренней сферы φ₂ определяется известным соотношением:

$[ varphi_2 = frac{q}{4pivarepsilon_0 r}. ]$

Тогда общий потенциал φ_inна поверхности внутренней сферы равен:

$[ varphi_{in} = varphi_1 + varphi_2 = frac{1}{4pivarepsilon_0}left(frac{Q}{R}+frac{q}{r}right). ]$

Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’₁ и собственно внешней сферы φ’₂.

Потенциал внутренней сферы φ’₁ на расстоянии R от ее центра определяется известным соотношением:

$[ varphi'_1 = frac{q}{4pivarepsilon_0 R}. ]$

Формула, определяющая потенциал внешней сферы φ’₂ на ее поверхности, также хорошо известна:

$[ varphi'_2 = frac{Q}{4pivarepsilon_0 R}. ]$

Тогда общий потенциал на поверхности внешней сферы равен:

$[ varphi_{ex} = varphi'_1 + varphi'_2 = frac{q+Q}{4piepsilon_0 R}. ]$

Задача 2. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R₂. Определите потенциал шара φ₁ после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.

Решение. До соединения сфер проводником заряд первой был равен:

$[ q=frac{varphi R_1}{k}. ]$

После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:

$[ varphi_1 = kfrac{q_1+q_2}{R_2}, ]$

где q₁ и q₂ — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q₁ + q₂. После несложных преобразований получаем:

$[ varphi_1 = kfrac{q}{R_2} = varphifrac{R_1}{R_2}. ]$

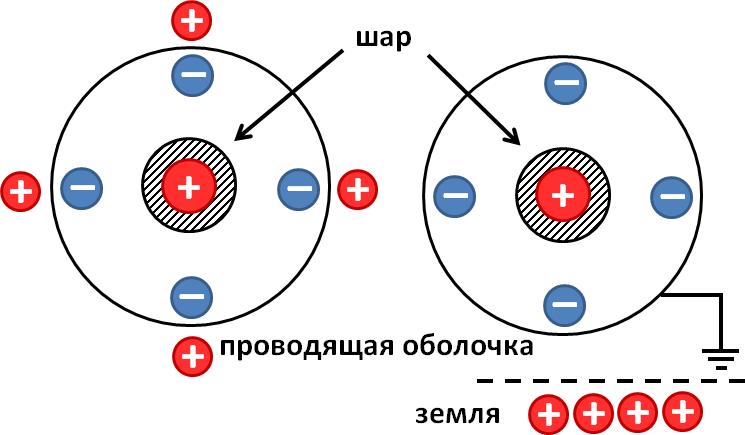
Задача 3. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R₂. Чему станет равен потенциал шара φ‘, если заземлить оболочку?

Начнем с рисунка к решению задачи:

После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы

Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:

$[ q = frac{varphi R_1}{k}. ]$

Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.

В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q₂, поскольку он притягивается к положительному заряду q₁ внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:

$[ kfrac{q_1+q_2}{R_2} = 0Leftrightarrow q_1 = q = - q_2. ]$

Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:

$[ varphi' = kleft(frac{q_1}{R_1}+frac{q_2}{R_2}right) = ]$

$[ = kleft(frac{q}{R_1}-frac{q}{R_2}right) =varphileft(1-frac{R_1}{R_2}right). ]$

Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.

Репетитор по физике и математике
Сергей Валерьевич

Источник

Проводящие сферы в электростатике

Задачи с
проводящими сферами можно успешно решать имея знания в пределах школьной
программы. Проводниками называют такие материалы, в которых имеются свободные
носители зарядов. Если сообщить заряд проводящему телу то свободные заряды
перестают перемещаться вдоль поверхности проводящего тела при достижении такого
их распределения, при котором вектор напряженности электрического поля в любой
точке перпендикулярен поверхности тела. Поэтому в электрическом поле
поверхность проводящего тела любой формы является эквипотенциальной
поверхностью. Все точки внутри проводника имеют одинаковый потенциал, равный
потенциалу на его поверхности. Если заряд на поверхности проводящего шара равен
q, то электрическое поле вне шара такое же, как поле точечного заряда q
находящегося в центре проводящего шара. Напряженность и потенциал графически
распределены на рисунке. Потенциал сферы .
Энергия уеденного проводника для сферы

Задача 1. В
системе, состоящей из двух концентрических проводящих сфер радиусом R и 3R (рис.),
внутренняя сфера соединена с землей через источник с ЭДС ε. Заряд
внешней сферы +2q. На расстоянии 2R от центра системы находится точечный
заряд –q.
Зная величины q, ε, R,
определите заряд внутренней сферы. Потенциал земли принять равным нулю.

Потенциал
внутренней сферы равен – ε. Сдругой стороны или

Отсюда

Задача 2. Три концентрические
проводящие сферы имеют расдиусы R, 2R и 3R. Внутренняя и внешняя не заряжены,
заряд средней сферы равен q₀. В некоторый
момент внутреннюю и внешнюю сферы соединяют проволокой (рис). Какой заряд
пройдет по этой проволоке, и какое при этом выделится количество теплоты?

При соединении
внутренней и внешней сферы электроны перетекают до тех пор пока потенциалы сфер
сравняются. В результате заряд внешней сферы обозначим q а внутренней -q.
Определим потенциалы сфер. Внутренней

Внешней .
Т.к. φ₁ = φ₃ получим

Так как до
соединения на внутренней и внешней сферах зарядов не было следовательно заряд
прошедший по проволоке . По закону сохранения
энергии W₁ = W₂ + Q Q = W₁ – W₂. Энергия сферы
это энергия электрического поля в пространстве вокруг сферы сферы

заменив q получим . Следовательно

Задача 3. Внутри
проводящей сферы радиусом R, имеющей заряд q, концентрично с ней расположена
сфера радиусом r (рис.). внутренняя сфера тонким длинным изолированным
проводом, проходящим через маленькое отверстие во внешней сфере, с помощью
ключа К заземлена. Найдите максимальное количество теплоты, которое может
выделиться, если ключ К перевести из положения 1 в положение 2, соединив тем
самым внутреннюю сферу с землей через источник с ЭДС ε.

Потенциал любой
точки соединенной с Землей равен нулю, следовательно в положении ключа 1
потенциал внутренней сферы равен 0. отсюда
. В положении ключа 2 потенциал этой сферы
ε

отсюда

Работа источника

Начальная энергия

Конечная . По закону
сохранения энергии Q = A + W₁ – W₂
подставив выражения получим

Задача 4. Проводящий шар заряжают некоторым зарядом Q и при помощи
длинной очень тонкой проволоки соединяют с незаряженным проводящим шаром втрое
меньшего радиуса, расположенным очень далеко. Максимальное значение силы тока
оказывается при этом равным I. Каким будет это значение в другом опыте – когда
вначале каждый из зарядов первого и второго шара равен Q? Сопротивление
проволоки мало.

Проволоку соединяющую шары можно представить как индуктивность L.
Ток в ней максимален когда ε₁ = 0. Значит в этот момент потенциалы сфер
равны или Q₁ = 3Q₂.

По закону
сохранения заряда Q = Q₁ + Q₂ и Q = 4Q₂ .

Из закона
сохранения энергии

Отсюда

Во втором случае

Q₃ = 3Q₄ 2Q = Q₃ + Q₄ Из
закона сохранения энергии

Отсюда

Упражнения

1. Проводящие
концентрические сферы имеют радиусы R и 3R, на расстоянии 2R от их
общего центра находится точечный заряд Q. Сферы соединяют между собой
тонким проводом, и получившийся проводник заземляют тонким проводником,
имеющим большое сопротивление. Какой заряд протечет по этому проводнику? Какое
количество теплоты выделится в системе за большое время?

(Ответ )

2. Две
тонкостенные металлические сферы, радиусы которых R₁ = 20см и R₂ = 40см,
образуют сферический конденсатор (рис). На внешней сферы находится заряд Q = 10^-8
Кл. Внутренняя сфера не заряжена. Какой заряд протечет через гальванометр Г,
если замкнуть ключ К.

(Ответ )

3. Сферический
конденсатор радиус внутренней обкладки которого r, а внешней R,
подключен к батарее ЭДС которой ε, а внутреннее сопротивление r. Первоначально
внешняя обкладка конденсатора была заземлена с помощью ключа К как показано на
рис. Найдите количество теплоты которое может выделится на внутреннем
сопротивлении батареи после переключения ключа в положение 2. Считать, что
конденсатор находится достаточно далеко от других предметов, а соединительные
провода очень тонкие.

4. На трех
металлических сферах радиусами r₁ < r₂ < r₃
размещены заряды соответственно q₁, q₂, q₃ (рис). В
некоторой точке А, расположенной между первой и второй сферами на расстоянии r
от центра, измеряется потенциал. Чему равен этот потенциал в следующих случаях
1) Ключи К₁ и К₂ разомкнуты 2) после замыкания ключа К₁
3) после замыкания ключа К₂ при замкнутом ключе К₁?

Источник