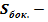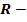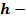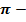Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Определение.
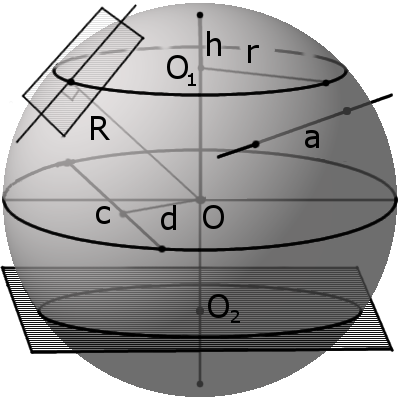
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
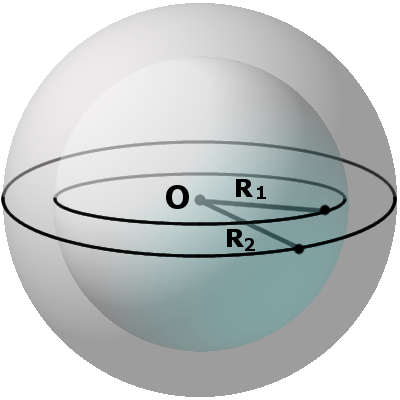
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара:
| V = | 4 | πR3 = | 1 | πD3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:
x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x0, y0, z0) в декартовой системе координат:
(x — x0)2 + (y — y0)2 + (z — z0)2 = R2
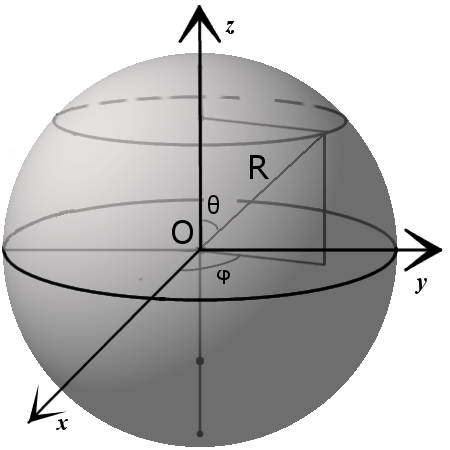
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
x = x0 + R · sin θ · cos φ
y = y0 + R · sin θ · sin φ
z = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 — m2,
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
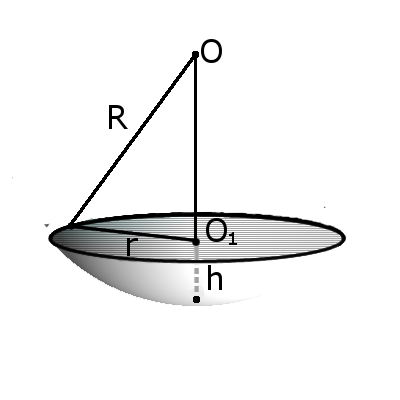
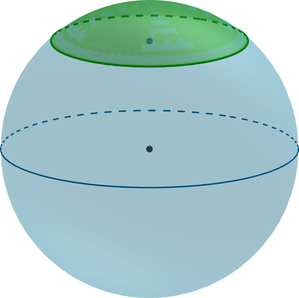
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
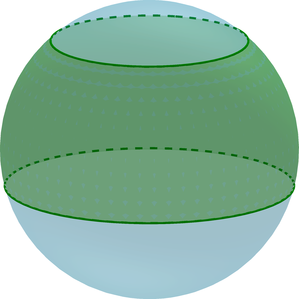
Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
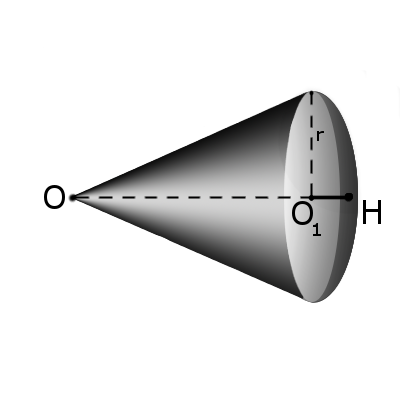
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR — h2)
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
({color{red}{{small{textbf{Факт 1. Про шаровой сегмент}}}}})
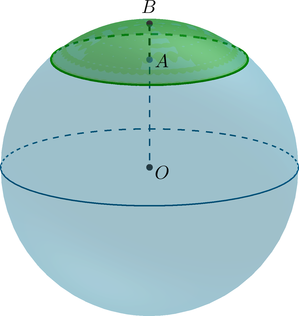
(bullet) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью ((alpha)).
(bullet) Если (O) – центр шара, (OB=R) – радиус шара, перпендикулярный плоскости (alpha), (A) – центр круга (основания шарового сегмента), а также точка пересечения радиуса (OB) c этим кругом, то
(H=AB) – высота шарового сегмента.
(bullet) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью (alpha)) вычисляется по формуле [S=2pi cdot RH] (bullet) Объем шарового сегмента вычисляется по формуле [V=pi H^2cdot left(R-frac13Hright)]
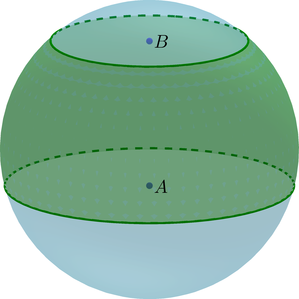
({color{red}{{small{textbf{Факт 2. Про шаровой слой}}}}})
(bullet) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.
(bullet) Основания шарового слоя – это сечения шара плоскостями.
(bullet) Высота (H=AB) шарового слоя – это расстояние между основаниями.
(bullet) Площадь сферической части шарового слоя равна [S=2pi RH] где (R) – радиус шара.
(bullet) Объем шарового слоя равен разности объемов двух шаровых сегментов: [V=V_{A}-V_{B}]
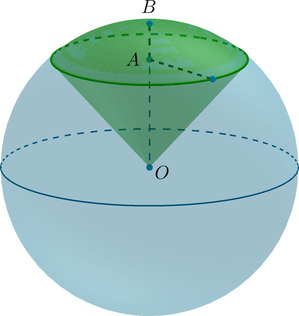
({color{red}{{small{textbf{Факт 3. Про шаровой сектор}}}}})
(bullet) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.
(bullet) Если (H=AB), то объем шарового сектора равен [V=dfrac23pi R^2cdot H]
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x — x 0) 2 + ( y — y 0) 2 + ( z — z 0) 2 = R 2
Основные свойства сферы и шара
Секущая, хорда, секущая плоскость сферы и их свойства
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Касательная, касательная плоскость к сфере и их свойства
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
S = π R(2 h + √ 2 h R — h 2 )
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение радиуса шара: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус шара и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса шара
1. Через объем
Радиус шара вычисляется по формуле:
V – объем шара; равен трем четвертым произведения его радиуса в кубе и числа π .
π – число, приближенное значение которого равняется 3,14.
2. Через площадь поверхности
Радиус шара рассчитывается таким образом:
S – площадь поверхности шара; равна четырем его радиусам в квадрате, умноженным на число π .
S = 4 π R 2
Примеры задач
Задание 1
Объем шара составляет 904,32 см 3 . Найдите его радиус.
Решение:
Воспользовавшись первой формулой получаем:
Задание 2
Вычислите радиус шара, если площадь его поверхности равна 314 см 2 .
Решение:
В данном случае рассчитать радиус шара можно, применив 2-ю формулу (через площадь поверхности):
Площадь поверхности шара формула и калькулятор онлайн
Что такое шар?
В стереометрии есть большой раздел, который называется фигуры вращения. Об этом редко говорят в школе, но плоские фигуры можно вращать вокруг какой-либо оси или точки. Так получаются объемные фигуры.
Стереометрия это наука о фигурах в пространстве. Простейшими единицами стереометрии является точка, прямая и плоскость.
Например, цилиндр образован вращением прямоугольника или квадрата. Поэтому, если рассечь цилиндр плоскостью, то сечение примет форму того самого квадрата или прямоугольника, который вращали, чтобы получить фигуру.
Так же и шар образован вращением. Как не трудно догадаться, основной для шара послужил круг. Причем сразу стоит сказать, что именно круг, а не окружность.
Следует понимать, что круг и окружность разные фигуры. Так окружность представляет собой набор точек равноудаленных от центра. Переводя на более простой язык окружность – это сама линия и центр окружности. А круг включает в себя и все внутреннее пространство. У окружности не может быть площади.
То есть, шар имеет какое-то внутренне заполненное пространство. Интересно, что сфера так же имеет пространство внутри, только условно полое.
Формулы для вычисления радиуса
- Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см. Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).
- Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см.
- Такая же формула используется при вычислении радиуса и длины окружности круга.
- Например, дан шар с объемом 100 см 3 . Радиус этого шара вычисляется так:
- ((V/π)(3/4)) 1/3 = r
- ((100/π)(3/4)) 1/3 = r
- ((31,83)(3/4)) 1/3 = r
- (23,87) 1/3 = r
- 2,88 см = r
- Например, дан шар с площадью поверхности 1200 см 3 . Радиус этого шара вычисляется так:
- √(A/(4π)) = r
- √(1200/(4π)) = r
- √(300/(π)) = r
- √(95,49) = r
- 9,77 см = r
V = 4/3 πr3,
где V — объем, r — радиус шара.
Отсюда, радиус шара равен корню кубическому из объема шара деленного на три четвертых Пи:
Определение радиуса сферы при помощи площади ее поверхности
Допустим, нам дана сфера вместе с площадью её поверхности. В таком случае мы будем использовать формулу площади её поверхности для того, чтобы вычислить радиус.
где S – это площадь поверхности сферы, число Пи = 3,14.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.
Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
- S = 4 * 3,14 * 10²;
- S мяча равна ≈ 1256 см².
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс , у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .
По той же причине всю сферу можно рассматривать как сферический пояс , у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Высотой шарового сектора называют высоту его сферического сегмента .
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы .
Объем шара через длину окружности
Формула для нахождения объема шара через длину окружности: <6pi^3>> , где L — длина окружности шара.
Эта формула легко выводится формулы объема шара через его радиус и формулы для нахождения длины окружности
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
3. Параметрическое уравнение сферы с центром в точке ( x 0, y 0, z 0):
x = x 0 + R · sin θ · cos φ y = y 0 + R · sin θ · sin φ z = z 0 + R · cos θ
где θ ϵ [0, π ], φ ϵ [0,2 π ].
Определение радиуса сферы при помощи объема шара
Если нам дан объём шара, ограниченного сферой, то радиус находится так:
где V – это объём шара, число Пи = 3,14.
Определение основных величин
- Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу.
- Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара.
- Объем (V) – это значение трехмерного пространства, занимаемого шаром. [6]
- Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара.
- Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.
- D = 2г. Как и в случае круга , диаметр шара в два раза больше его радиуса.
- C = πD = 2πr. Как и в случае круга , длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара.
- V = (4/3)πr 3 . Объем шара равен произведению 4/3 на π и на радиус в кубе. [7]
- А = 4πr 2 . Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr 2 , то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.
r = С / 2π
π — величина постоянная, равна отношению длины окружности к диаметру. Число Пи, равное 3,141592653… обычно округляется до 3,14.
— по площади шара.
Площадь шара равна произведению четырех пи на квадрат радиуса:
Нахождение радиуса по расстоянию между двумя точками
- Рассмотрим пример. Дан шар с центром с координатами (4,-1,12). Воспользуйтесь этими координатами, чтобы найти радиус шара.
- В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0). Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.
- В рассматриваемом примере вместо (x1,y1,z1) подставьте (4,-1,12), а вместо (x2,y2,z2) подставьте (3,3,0):
- d = √((x2 – x1) 2 + (y2 – y1) 2 + (z2 – z1) 2 )
- d = √((3 – 4) 2 + (3 – -1) 2 + (0 – 12) 2 )
- d = √((-1) 2 + (4) 2 + (-12) 2 )
- d = √(1 + 16 + 144)
- d = √(161)
- d = 12,69. Это искомый радиус шара.
- Возведите обе стороны этого уравнения в квадрат, и получите r 2 = (x2 – x1) 2 + (y2 – y1) 2 + (z2 – z1) 2 . Отметьте, что это уравнение соответствует уравнению сферы r 2 = x 2 + y 2 + z 2 с центром с координатами (0,0,0).
C = πD = 2πr
Отсюда, радиус равен частному от деления длины окружности © на 2 пи:
Через площадь поверхности
Радиус шара рассчитывается таким образом:
S – площадь поверхности шара; равна четырем его радиусам в квадрате, умноженным на число π .
S = 4 π R 2
Одиннадцать свойств
В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:
- Точки на сфере находятся на одинаковом расстоянии от одной фиксированной, называемой центром. Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
- Контуры и плоские участки сферы являются кругами. Это однозначное свойство, которое определяет шар.
- Сфера имеет постоянную ширину и обхват. Ширина поверхности — это расстояние между парами параллельных касательных плоскостей. Множество других замкнутых выпуклых поверхностей имеют постоянную ширину, например, тело Мейснера. Обхват поверхности — это окружность границы её ортогональной проекции на плоскость. Каждое из этих свойств подразумевает другое.
- Все точки сферы омбилические. В любой точке поверхности вектор нормали расположен под прямым углом к ней, поскольку шар — это линии, выходящие из его центра. Пересечение плоскости, которая содержит нормаль с поверхностью, сформирует кривую — нормальное сечение. Любая замкнутая поверхность будет иметь как минимум четыре точки, называемых омбилическими. Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
- У шара нет центра поверхности. Например, два центра, соответствующие минимальной и максимальной секционной кривизне, называются фокальными точками, а совокупность всех таких точек образует одноимённую поверхность. И только у шара она преобразуется в единую точку.
- Все геодезические сферы являются замкнутыми кривыми. Для этой фигуры они большие круги. Многие другие поверхности разделяют это свойство.
- Имеет наименьшую площадь при наибольшем объёме. Это определяет шар однозначно. Например, мыльный пузырь: его окружает фиксированный объём, поверхностное натяжение минимизирует площадь его поверхности для такого объёма. Конечно, пузырь не будет идеальным шаром, поскольку внешние силы, такие как гравитация, будут искажать его форму.
- Сфера — единственная вложенная поверхность, у которой нет границы или сингулярностей с постоянной положительной средней кривизной.
- Сфера имеет наименьшую общую среднюю кривизну среди всех выпуклых тел с заданной площадью поверхности.
- Шар имеет постоянную гауссову кривизну. Это внутреннее свойство, которое определяется путём измерения длины и углов и не зависит от того, как поверхность встроена в пространство.
Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.
http://exceltut.ru/ploshhad-poverhnosti-shara-formula-i-kalkulyator-onlajn/
Шаровой сектор представляет собой совокупное тело, полученное путем соединения шарового сегмента и конуса с одним и тем же основанием, с учетом того что, вершина конуса находится в центре первоначальной сферы.
Диаметр шарового сектора является по совместительству диаметром первоначальной сферы, поэтому он рассчитывается через больший радиус шарового сектора.
D=2R
При необходимости можно найти и периметр окружности, лежащей в основании шарового сегмента и конуса, из которых состоит шаровой сектор, умножив меньший радиус на удвоенное число π.
P=2πr
Для того чтобы вычислить площадь поверхности шарового сектора, нужно найти площадь поверхности шарового сегмента и боковую площадь поверхности конуса. Для этого необходимо знать радиус и высоту шарового сектора. В ходе преобразований данной суммы, площадь поверхности шарового сектора становится равна следующему выражению.
S=πR(2(R-√(R^2-r^2 ))+r)
Чтобы найти объем шарового сектора, зная высоту шарового сегмента и радиус сферы, нужно умножить произведение числа π, квадрата большего из двух радиусов и высоты сегмента на две трети.
V=2/3 πR^2 H
Шаровый сегмент. Шаровый сектор
Рис. 4.
Радиус шара –любой отрезок, соединяющий центр и какую-нибудь точку сферы.
Диаметр шара –отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы равен 2R.
Центр шара – точка О.
Теорема: Объем шара радиуса R равен
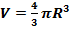
где 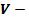
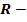
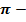
|
Части шара |
Шаровый сегмент
часть шара отсекаемая от него какой-нибудь плоскостью
Шаровый сектор
тело, полученное вращением кругового сектора с углом, меньшим 
часть шара, заключенная между двумя параллельными секущими плоскостями
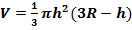
где V 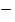
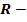
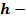
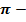
Объем шарового сектора:
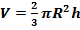
где V 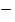
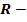
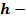
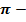
Объем шарового слоя:
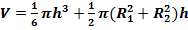
где 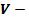
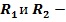
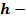
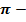
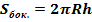
где 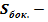
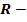
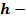
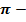
3, 14.
Площадь полной поверхности:
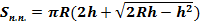
где 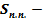
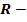
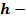
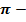
Площадь боковой поверхности:
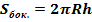
где