Как найти радиус сферы вписанного в параллелепипед - Исправление недочетов и поиск решений вместе с Examum.ru

Определите и запишите основную мысль текста.
(1)Чёрный аист — лесной отшельник: немногие видели его в лесу, не любит он напоказ выставляться, разве что когда в небе пари́ т. (2)Но чёрный аист не такой уж и чёрный. (3)Брюхо, бока, надкрылья у него нежно-белые. (4)Клювище красный, а длинные ноги алые. (5)Чёрный он только в тени, а на солнце полыхает то зеленью, то синевой, а то и багрянцем. (6)Аист важно вышагивает среди теней и бликов леса и, как драгоценный камень, всё время изменяется в цвете.

(7)Плавал я раз в глухом лесном озерке. (8)Рыбьи мальки щипали губами бока, и я разгонял их, чтобы не щекотали, но особенно почему-то доставалось ногам, обутым в красные ласты: мальки облепили их, как комары. (9)Когда я поднял глаза, то на другом берегу увидел трёх чёрных аистов: они стояли по колено в воде, окунув клювы в воду. (10)Конечно, они тоже меня заметили и взлетели. (11)На берегу, где они топтались, остались белые кляксы и разлапистые следы, а в воде, где они стояли, роились мальки.

(12)Я вспомнил про красные ласты: выходит, аисты красными своими ногами и носами приманивали мальков. (13)Я окунул в воду красные ласты, и мальки снова мгновенно облепили их. (14)И в самом деле необычный окрас аистов помогает им добывать пищу.

(По Н. Сладкову)

Задание:

Какой факт, по мнению автора текста, свидетельствует о том, что чёрный аист— лесной отшельник? Запишите ответ.

Определите, какой тип речи представлен в предложениях 2−4 текста. Запишите ответ.

В предложениях 7−9 найдите слово со значением «край суши, прилегающий к водоёму». Выпишите это слово.

В предложениях 3−5 найдите антоним к слову «короткие» и выпишите его.

Источник

Скачать материал

Сейчас обучается 388 человек из 63 регионов

Сейчас обучается 267 человек из 65 регионов

Описание презентации по отдельным слайдам:

1 слайд

Реферат
на тему «Вписанные и описанные многогранники»
(Математика)
Выполнили:
ученицы 11 класса Б
гимназии № 12
Злова Виктория и
Обедина Екатерина

Проверила:
Третьякова Н. А.
2 слайд

Цель работы состоит в том, чтобы узнать весь теоретический материал по теме «Вписанные и описанные многогранники» и научиться применять его на практике.
Цель реферата
3 слайд

Правильные многогранники
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
4 слайд

Многогранники, вписанные в шар
Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника. Центр этой сферы является точкой, равноудаленной от вершин многогранника. Она является точкой пересечения плоскостей, каждая из которых проходит через середину ребра многогранника перпендикулярно ему.
5 слайд

Пирамида, вписанная в шар
Теорема:
Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.
6 слайд

Формула для нахождения радиуса описанной сферы
Пусть SABC — пирамида с равными боковыми ребрами, h — ее высота, R — радиус окружности, описанной около основания. Найдем радиус описанной сферы.
Заметим подобие прямоугольных треугольников SKO1 и SAO.
Тогда
SO1/SA = KS/SO;
R1 = KS · SA/SO
Но KS = SA/2.
Тогда
R1 = SA2/(2SO);
R1 = (h2 +R2)/(2h);
R1 = b2/(2h), где b — боковое ребро.
7 слайд

Призма, вписанная в шар
Теорема:
Около призмы можно описать шар только в том случае, если призма является прямой и около ее основания можно описать окружность.
8 слайд

Параллелепипед, вписанный в шар
Теорема:
Сфера может быть описана около параллелепипеда тогда и только тогда, когда параллелепипед прямоугольный, так как в данном случае он является прямым и около его основания — параллелограмма — может быть описана окружность (т. к. основание — прямоугольник).
9 слайд

Конус и цилиндр, вписанные в шар
Теорема:
Около всякого конуса можно описать сферу.
Теорема:
Около любого цилиндра можно описать сферу.
10 слайд

Задача 1
Найти радиус шара, описанного около правильного тетраэдра с ребром а.
Решение:
SO1 = SA2/(2SO);
SO =
SO =
=
= a
SO1 = a2/(2 a
) = a
/4.
Ответ:
SO1 = a
/4.
Предварительно построим на изображении правильного тетраэдра SABC изображение центра описанного шара. Проведем апофемы SD и AD (SD = AD). В равнобедренном треугольнике ASD каждая точка медианы DN равноудалена от концов отрезка AS. Поэтому точка O1 есть пересечение высоты SO и отрезка DN.
Используя формулу из R1 = b2/(2h), получим:
11 слайд

Задача 2
Решение:
По формуле R1=b2/(2h) для нахождения радиуса описанного шара найдем SC и SO.
SC = a/(2sin(α/2));
SO2 = (a/(2sin(α/2))2 – (a
/2)2 =
= a2/(4sin2(α/2)) – 2a2/4 =
= a2/(4sin2(α/2)) · (1 – 2sin2(α/2)) =
= a2/(4sin2(α/2)) · cosα
В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найти радиус описанного шара.
R1 = a2/(4sin2(α/2)) · 1/(2a
/(2sin(α/2))) =
a/(4sin(α/2) ·
).
Ответ:
R1 = a/(4sin(α/2) ·
).
12 слайд

Многогранники, описанные около шара
Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника. Центром вписанной сферы является точка, равноудаленная от всех граней многогранника.
13 слайд

Положение центра вписанной сферы
Понятие биссекторной плоскости двугранного угла.
Биссекторной называется плоскость, делящая двугранный угол на два равных двугранных угла.
Каждая точка этой плоскости равноудалена от граней двугранного угла.
В общем случае центр вписанной в многогранник сферы является точкой пересечения биссекторных плоскостей всех двугранных углов многогранника. Он всегда лежит внутри многогранника.
14 слайд

Пирамида, описанная около шара
Шар, называется вписанным в (произвольную) пирамиду, если он касается всех граней пирамиды (как боковых, так и основания).
Теорема:
Если боковые грани одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.

Так как двугранные углы при основании равны, то их половинки тоже равны  биссектрисы пересекаются в одной точке на высоте пирамиды. Эта точка принадлежит всем биссекторным плоскостям при основании пирамиды и  равноудалена от всех граней пирамиды – центр вписанного шара.
15 слайд

Формула для нахождения радиуса вписанной сферы
Пусть SABC — пирамида с равными боковыми ребрами, h — ее высота, r — радиус вписанной окружности. Найдем радиус описанной сферы.
Пусть SO = h, OH = r, O1O = r1.
Тогда по свойству биссектрисы внутреннего угла треугольника
O1O/OH = O1S/SH;
r1/r = (h – r1)/ ;
r1 · = rh – rr1;
r1 · ( + r) = rh;
r1 = rh/( + r).
Ответ: r1 = rh/( + r).
16 слайд

Призма, описанная около шара
Теорема:
Сферу можно вписать в призму тогда и только тогда, когда призма прямая и в основание можно вписать окружность, диаметр которой равен высоте призмы.
17 слайд

Параллелепипед и куб, описанные около шара
Теорема:
В параллелепипед можно вписать сферу тогда и только тогда, когда параллелепипед прямой и его основание — ромб, причем высота этого ромба есть диаметр вписанной сферы, который, в свою очередь, равен высоте параллелепипеда. (Из всех параллелограммов только в ромб можно вписать окружность)
Теорема:
В куб всегда можно вписать сферу. Центр этой сферы — точка пересечения диагоналей куба, а радиус равен половине длины ребра куба.
18 слайд

Цилиндр и конус, описанные около шара
Теорема:
Сферу можно вписать лишь в такой цилиндр, высота которого равна диаметру основания.
Теорема:
Во всякий конус можно вписать сферу.
19 слайд

Комбинации фигур
Вписанная и описанная призмы
Призма, описанная около цилиндра – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.
Призма, вписанная в цилиндр – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра.
Касательная плоскость к цилиндру – плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
20 слайд

Вписанная и описанная пирамиды
Пирамида, вписанная в конус – пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса.
Боковые ребра пирамиды, вписанной в конус – образующие конуса.
Пирамида, описанная около конуса – пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса.
Плоскости боковых граней описанной пирамиды – касательные плоскости конуса.
Касательная плоскость к конусу – плоскость, проходящая через образующую и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
21 слайд

Другие виды конфигураций
Цилиндр вписан в пирамиду, если окружность одного его основания касается всех боковых граней пирамиды, а другое его основание лежит на основании пирамиды.
Конус вписан в призму, если его вершина лежит на верхнем основании призмы, а его основание – круг, вписанный в многоугольник – нижнее основание призмы.
Призма вписана в конус, если все вершины верхнего основания призмы лежат на боковой поверхности конуса, а нижнее основание призмы лежит на основании конуса.
22 слайд

Задача 1
В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найдите радиус вписанного в пирамиду шара.
Решение:
Выразим стороны ∆SOK через а и α.
OK = a/2.
SK = KC · ctg(α/2);
SK = (a · ctg(α/2))/2.
SO =
SO =
= (a/2)
Использую формулу r1 = rh/(
+ r), найдем радиус вписанного шара:
r1 = OK · SO/(SK + OK);
r1 = (a/2) · (a/2)
/((a/2) · ctg(α/2) + (a/2)) =
= (a/2)
/(ctg(α/2) + 1) =
(a/2)
=
= (a/2)
Ответ: r1 = (a/2)
23 слайд

Вывод
Тема «Многогранники» изучается учениками в 10 и 11 классах, но в учебной программе очень мало материала на тему «Вписанные и описанные многогранники», хотя она вызывает очень большой интерес у учащихся, так как изучение свойств многогранников способствует развитию абстрактного и логического мышления, что впоследствии пригодится нам в учебе, работе, жизни.
Работая над данным рефератом, мы изучили весь теоретический материал на тему «Вписанные и описанные многогранники», рассмотрели возможные комбинации фигур и научились применять весь изученный материал на практике.
Задачи на комбинацию тел – наиболее трудный вопрос курса стереометрии 11 класса. Но теперь мы с уверенностью можем сказать, что у нас не возникнет проблем при решении подобных задач, так как в ходе нашей исследовательской работы мы установили и доказали свойства вписанных и описанных многогранников. Очень часто у учащихся возникают трудности при построении чертежа к задаче на данную тему. Но, узнав, что для решения задач на комбинацию шара с многогранником изображение шара бывает излишним и достаточно указать его центр и радиус, мы можем быть уверены, что данных трудностей у нас не возникнет.
Благодаря данному реферату мы смогли разобраться в этой трудной, но очень увлекательной теме. Мы надеемся, что теперь у нас не возникнет трудностей при применении изученного материала на практике.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 268 750 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

13.12.2020
143
1

07.12.2020
287
4

07.12.2020
237
1

23.11.2020
486
1

08.10.2020
189
1

27.09.2020
156
0

26.09.2020
235
0

08.09.2020
143
0

Вам будут интересны эти курсы:

Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Основы построения коммуникаций в организации»
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
Курс повышения квалификации «Основы менеджмента в туризме»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
Курс профессиональной переподготовки «Организация маркетинговой деятельности»

Источник

Многогранники, вписанные в сферу

Многогранник называется вписанным в сферу, если все его вершины принадлежат этой сфере. Сама сфера при этом называется описанной около многогранника.

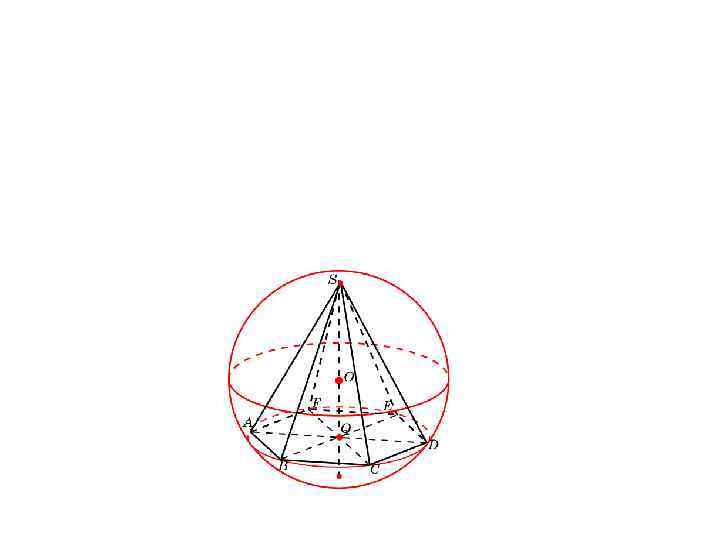
Теорема. Около пирамиды можно описать сферу тогда и только тогда, когда около основания этой пирамиды можно описать окружность.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Многогранники, вписанные в сферу

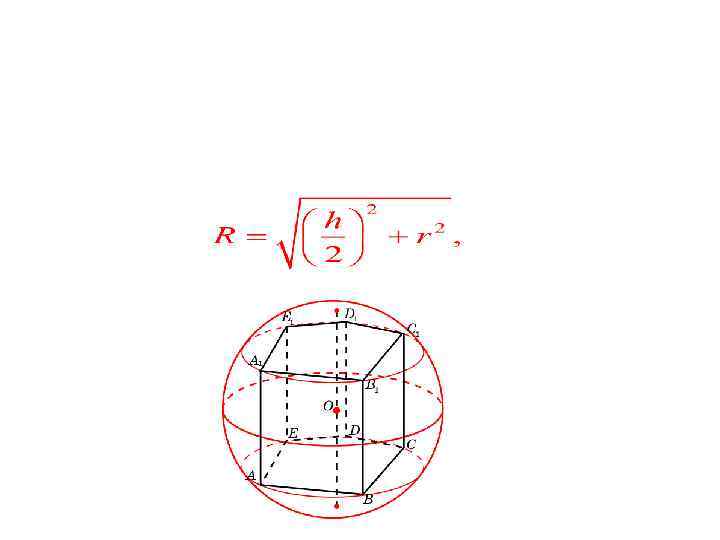
Теорема. Около призмы можно описать сферу тогда и только тогда, когда около основания этой призмы можно описать окружность. Ее центром будет точка O , являющаяся серединой отрезка, соединяющего центры окружностей, описанных около оснований призмы. Радиус сферы R вычисляется по формуле

где h – высота призмы, r – радиус окружности, описанной около основания призмы.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение 1

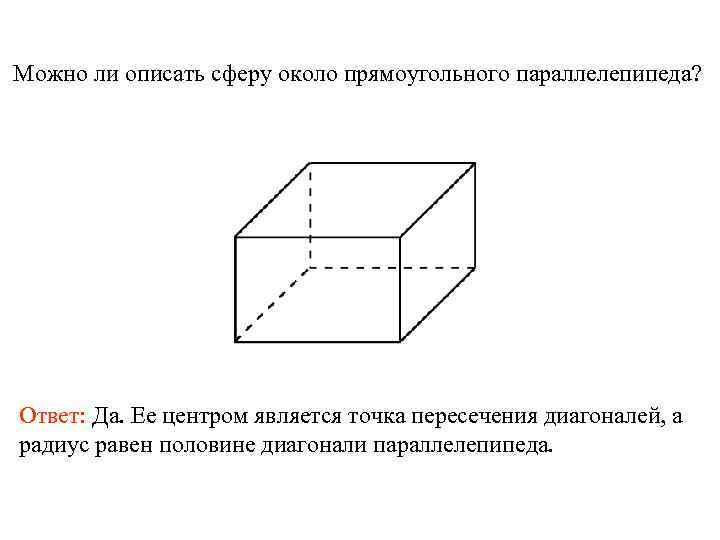
Можно ли описать сферу около прямоугольного параллелепипеда?

Ответ: Да. Ее центром является точка пересечения диагоналей, а радиус равен половине диагонали параллелепипеда

Упражнение 2

Можно ли описать сферу около наклонного параллелепипеда, все грани которого ромбы?

Ответ: Нет.

Упражнение 3

Можно ли описать сферу около наклонной призмы?

Ответ: Нет.

Упражнение 4

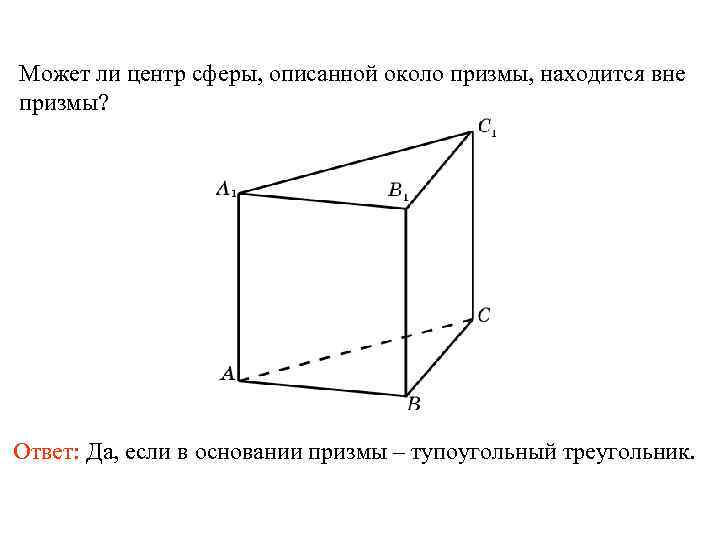
Может ли центр сферы, описанной около призмы, находится вне призмы?

Ответ: Да, если в основании призмы – тупоугольный треугольник.

Упражнение 5

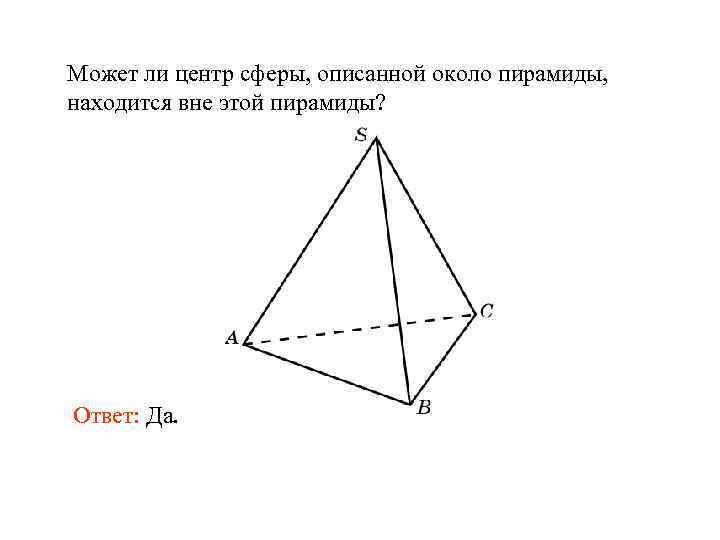
Может ли центр сферы, описанной около пирамиды, находится вне этой пирамиды?

Ответ: Да.

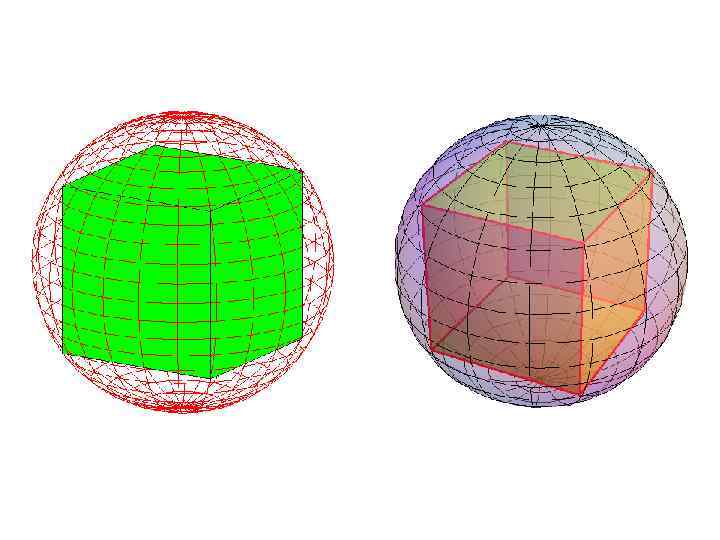
Сфера, описанная около куба

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение 1

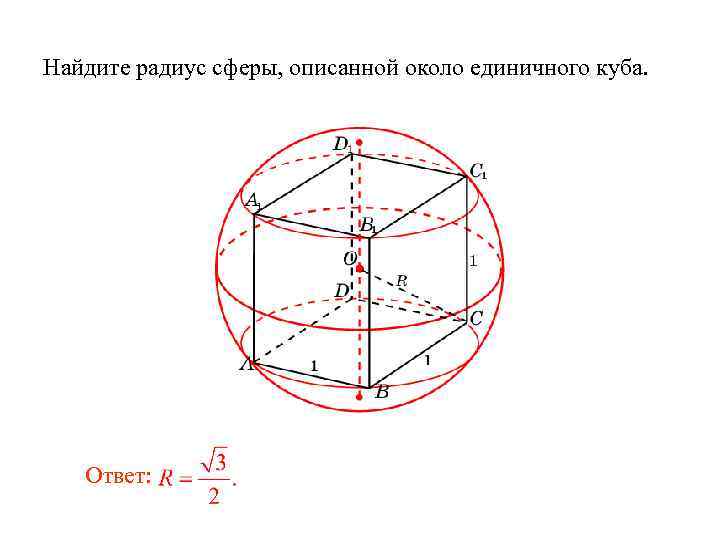
Найдите радиус сферы, описанной около единичного куба.

Ответ:

Упражнение 2

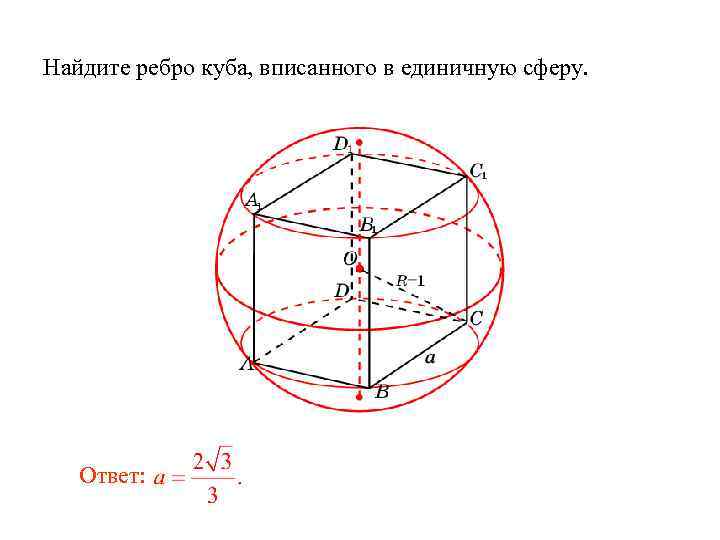
Найдите ребро куба, вписанного в единичную сферу.

Ответ:

Упражнение 3

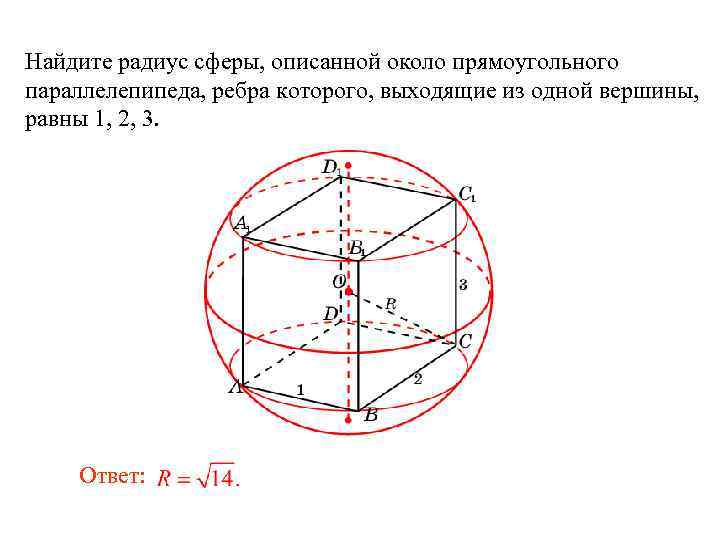
Найдите радиус сферы, описанной около прямоугольного параллелепипеда, ребра которого, выходящие из одной вершины, равны 1, 2, 3.

Ответ:

Упражнение 4

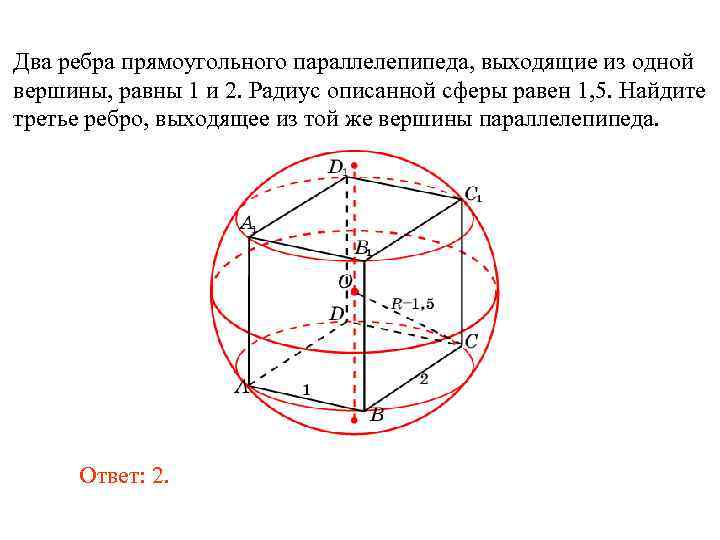
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 2. Радиус описанной сферы равен 1,5 . Найдите третье ребро, выходящее из той же вершины параллелепипеда.

Ответ: 2.

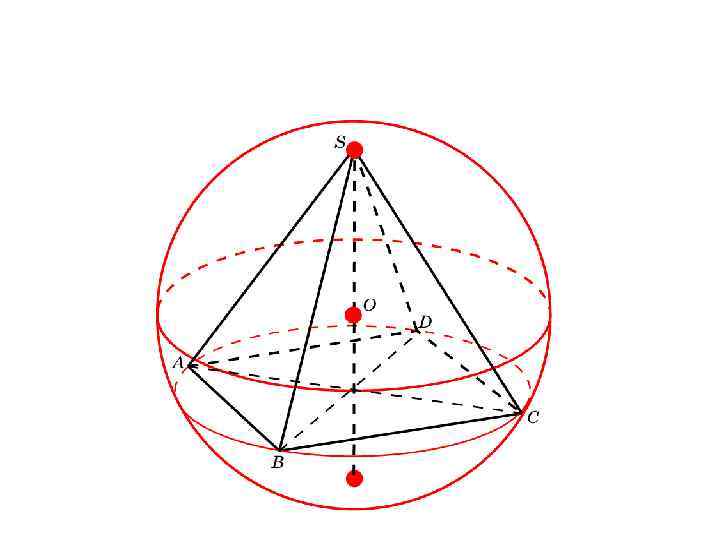
Сфера, описанная около тетраэдра

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение 1

Найдите радиус сферы, описанной около единичного тетраэдра.

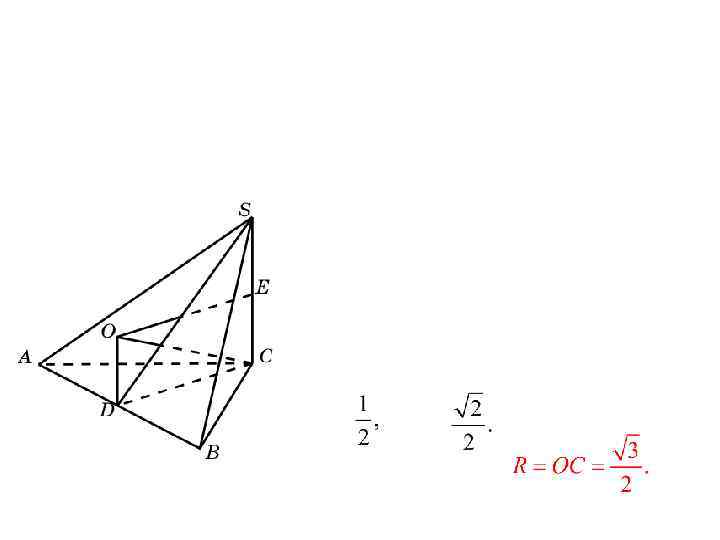
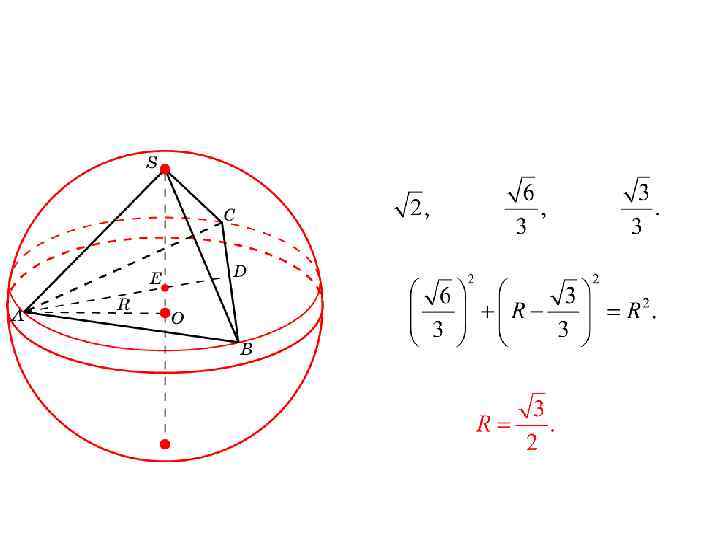
Решение. В тетраэдре SABC имеем:

BE = SE =

В прямоугольном треугольнике OBE имеем:

Решая это уравнение относительно R , находим

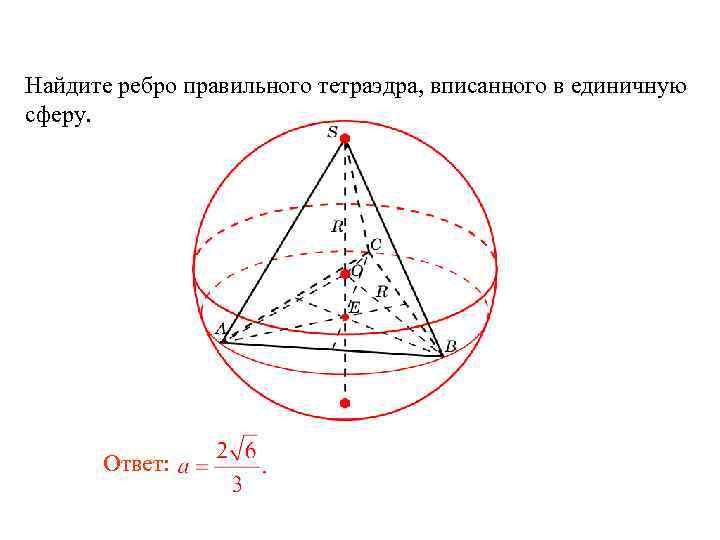
Упражнение 2

Найдите ребро правильного тетраэдра, вписанного в единичную сферу.

Ответ:

Упражнение 3

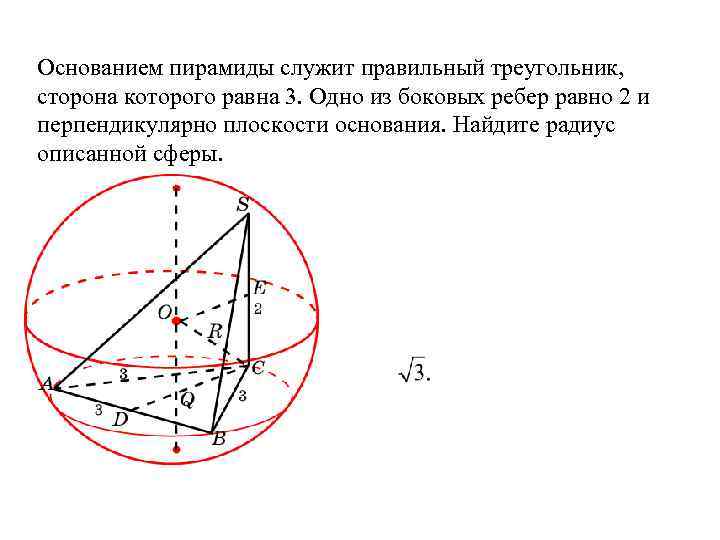
Основанием пирамиды служит правильный треугольник, сторона которого равна 3. Одно из боковых ребер равно 2 и перпендикулярно плоскости основания. Найдите радиус описанной сферы.

Решение. Пусть O – центр описанной сферы, Q – центр окружности, описанной около основания, E – середина SC . Четырехугольник CEOQ – прямоугольник, в котором CE = 1, CQ = Следовательно, R=OC= 2.

Ответ: R = 2.

Упражнение 4

На рисунке изображена пирамида SABC , для которой ребро SC равно 2 и перпендикулярно плоскости основания ABC , угол ACB равен 90 о , AC = BC = 1 . Постройте центр сферы, описанной около этой пирамиды и найдите ее радиус.

Решение. Через середину D ребра AB проведем прямую, параллельную SC . Через середину E ребра SC проведем прямую параллельную CD . Их точка пересечения O будет искомым центром описанной сферы. В прямоугольном треугольнике OCD имеем:

OD = CD = По теореме

Пифагора, находим

Упражнение 5

Найдите радиус сферы, описанной около правильной треугольной пирамиды, боковые ребра которой равны 1, и плоские углы при вершине равны 90 о .

Решение. В тетраэдре SABC имеем:

AB = AE = SE =

В прямоугольном треугольнике OAE имеем:

Решая это уравнение относительно R , находим

Сфера, описанная около треугольной призмы

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение 1

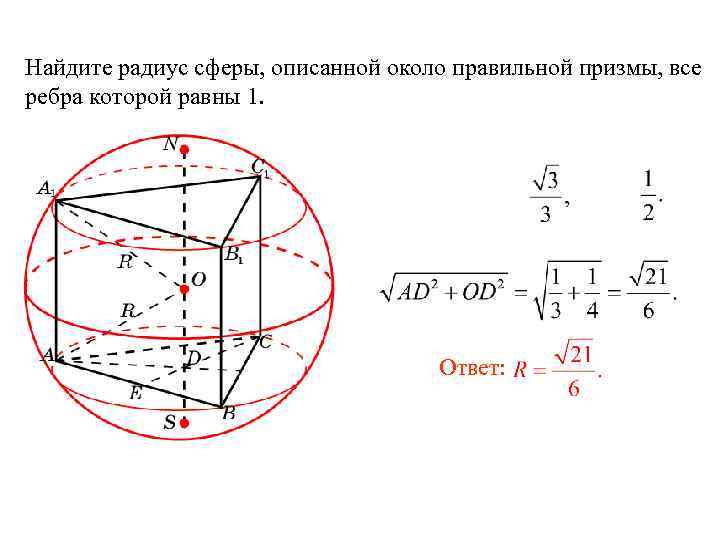
Найдите радиус сферы, описанной около правильной призмы, все ребра которой равны 1.

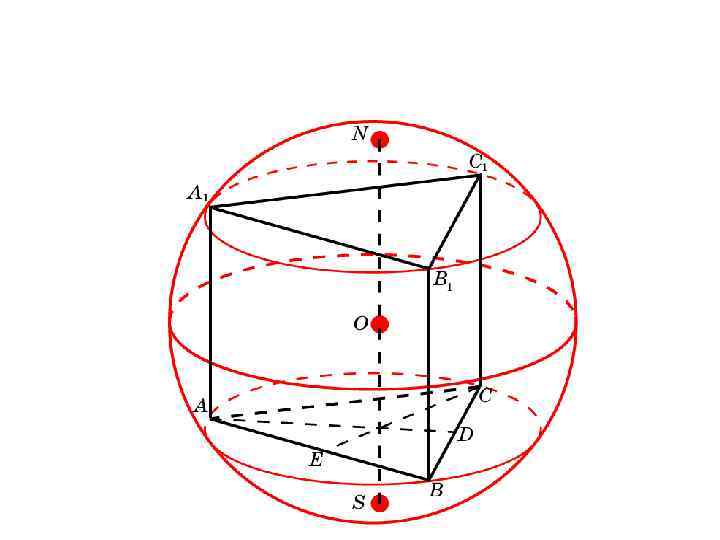
Решение. Имеем:

AA 1 = 1, AD = OD =

Следовательно, R = AO =

Ответ:

Упражнение 2

Около правильной треугольной призмы, сторона основания которой равна 1, описана сфера радиуса 2. Найдите высоту призмы.

Решение. Имеем: AO = 2, OD =

Следовательно, h = AA 1 = 2 AO =

Ответ:

Упражнение 3

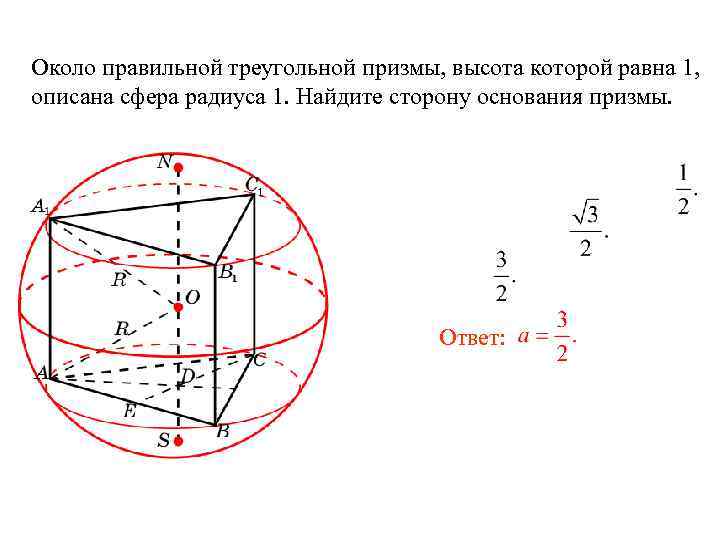
Около правильной треугольной призмы, высота которой равна 1, описана сфера радиуса 1. Найдите сторону основания призмы.

Решение. Имеем: AO = 1 , OD =

Следовательно, AD =

Значит, AB =

Ответ:

Упражнение 4

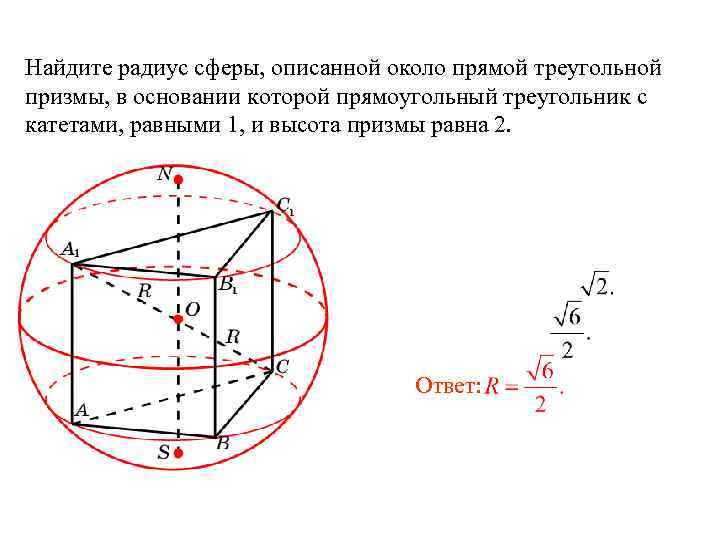
Найдите радиус сферы, описанной около прямой треугольной призмы, в основании которой прямоугольный треугольник с катетами, равными 1, и высота призмы равна 2.

Решение. Радиус сферы равен половине диагонали A 1 C прямоугольника ACC 1 A 1 .

Имеем: AA 1 = 2, AC =

Следовательно, R =

Ответ:

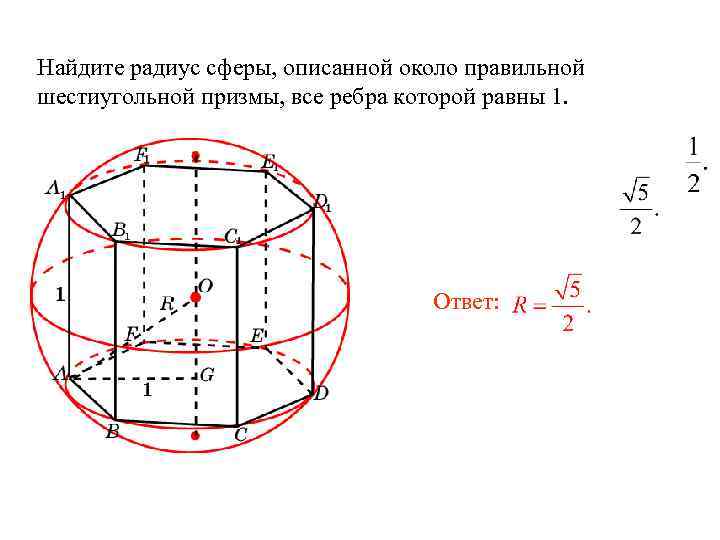
Сфера, описанная около правильной шестиугольной призмы

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение

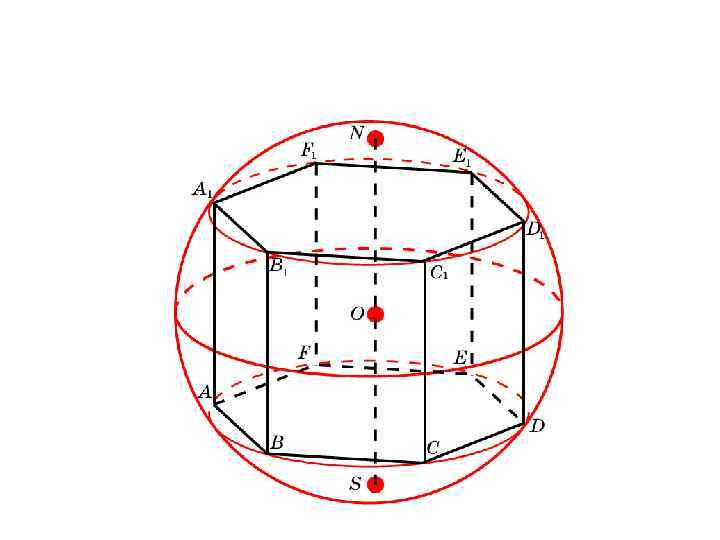
Найдите радиус сферы, описанной около правильной шестиугольной призмы, все ребра которой равны 1.

Решение. Имеем AG = 1, OG =

Следовательно, R=AO=

Ответ:

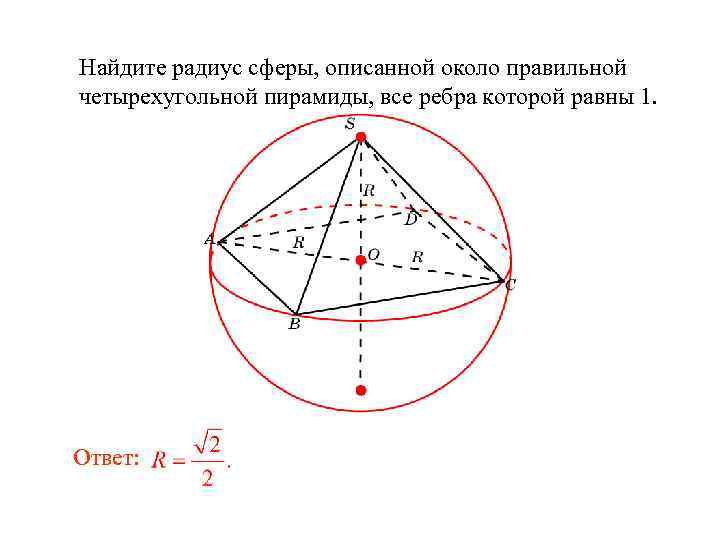
Сфера, описанная около правильной четырехугольной пирамиды

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение

Найдите радиус сферы, описанной около правильной четырехугольной пирамиды, все ребра которой равны 1.

Ответ:

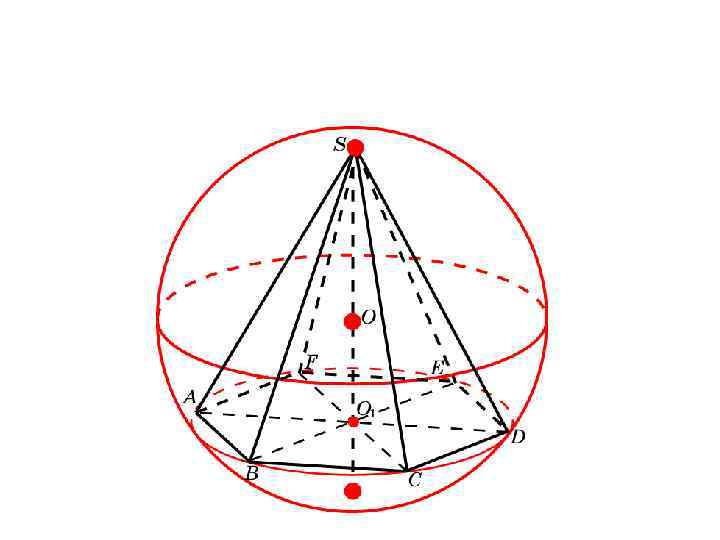
Сфера, описанная около правильной шестиугольной пирамиды

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение

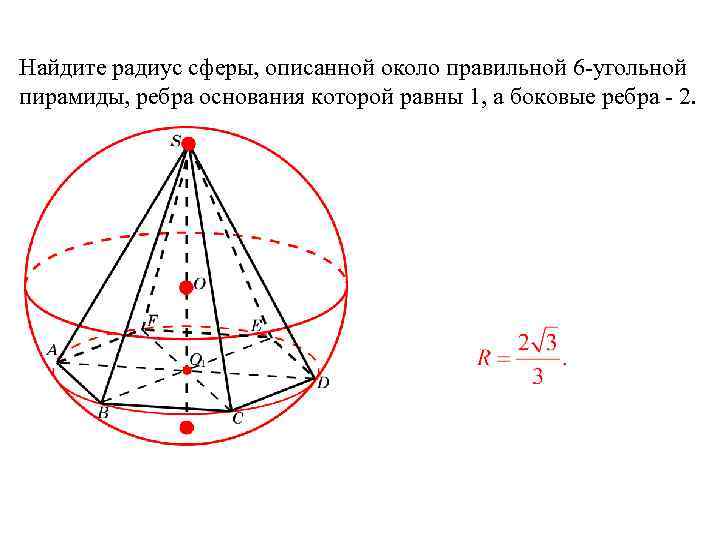
Найдите радиус сферы, описанной около правильной 6-угольной пирамиды, ребра основания которой равны 1, а боковые ребра — 2.

Решение. Треугольник SAD – равносторонний со стороной 2. Радиус R описанной сферы равен радиусу окружности, описанной около треугольника SAD . Следовательно,

Сфера, описанная около октаэдра

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение

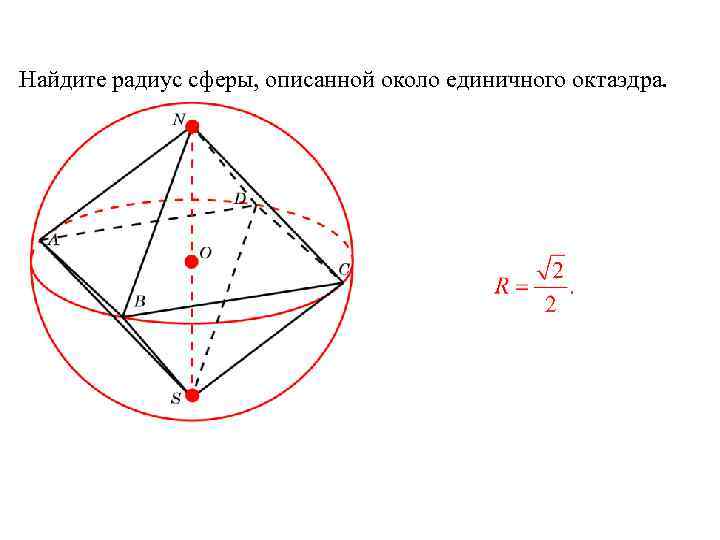
Найдите радиус сферы, описанной около единичного октаэдра.

Решение. Радиус R описанной сферы равен половине диагонали квадрата ABCD со стороной 1. Следовательно,

Сфера, описанная около икосаэдра

В режиме слайдов ответы и решения появляются после кликанья мышкой

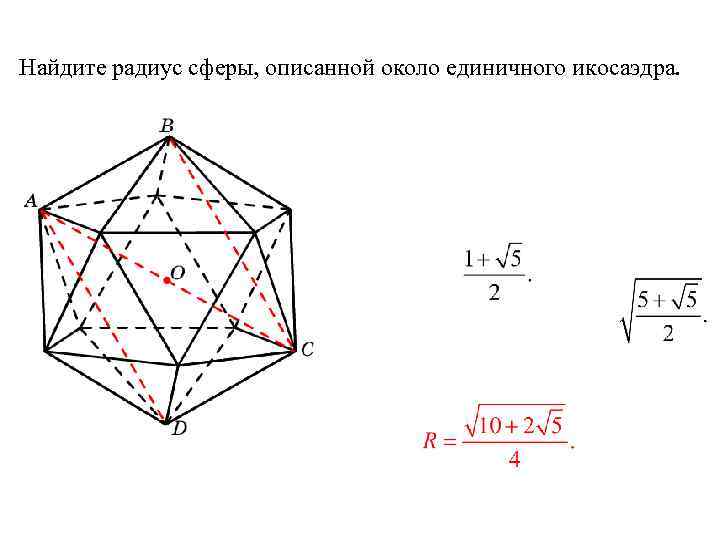
Упражнение

Найдите радиус сферы, описанной около единичного икосаэдра.

Решение. В прямоугольнике ABCD AB = CD = 1, BC и AD – диагонали правильных пятиугольников со сторонами 1. Следовательно,

BC = AD =

По теореме Пифагора AC =

Искомый радиус равен половине этой диагонали, т.е.

Сфера, описанная около додекаэдра

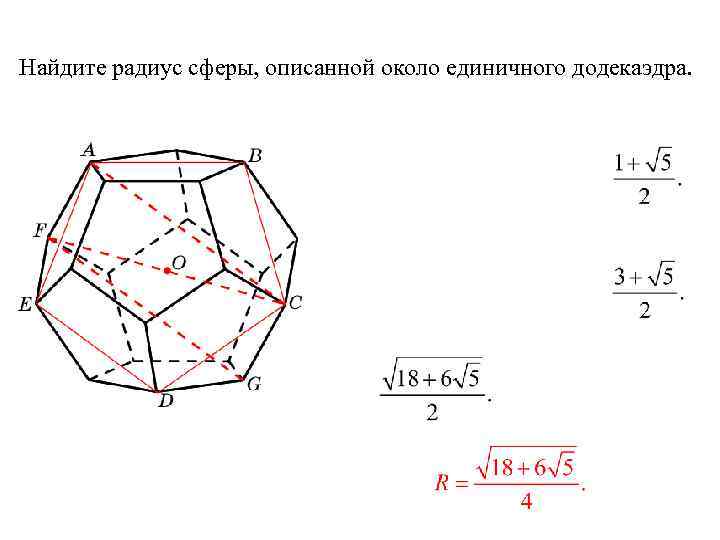
Упражнение

Найдите радиус сферы, описанной около единичного додекаэдра.

Решение. ABCDE – правильный пятиугольник со стороной

В прямоугольнике ACGF AF = CG = 1, AC и FG – диагонали пятиугольника ABCDE и, следовательно, AC = FG =

По теореме Пифагора

FC = Искомый радиус

равен половине этой диагонали, т.е.

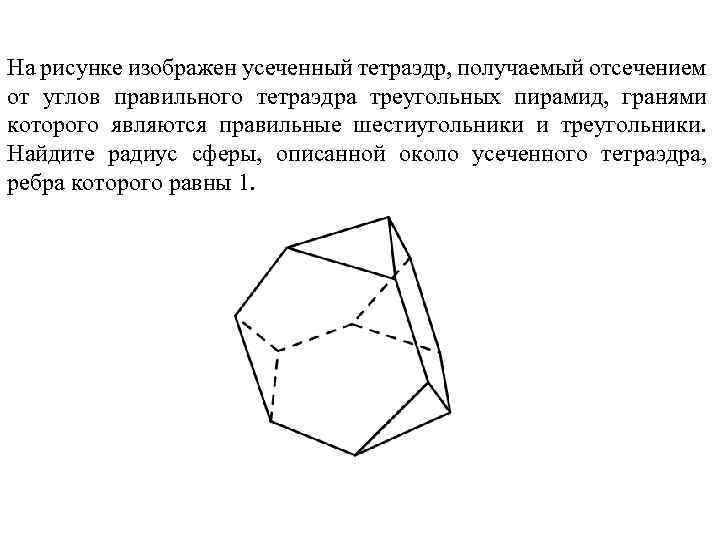
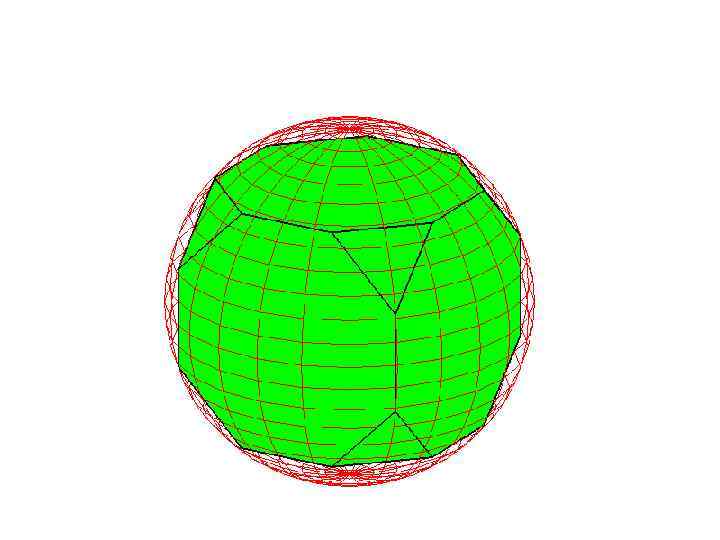
Сфера, описанная около усеченного тетраэдра

Упражнение

На рисунке изображен усеченный тетраэдр, получаемый отсечением от углов правильного тетраэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного тетраэдра, ребра которого равны 1.

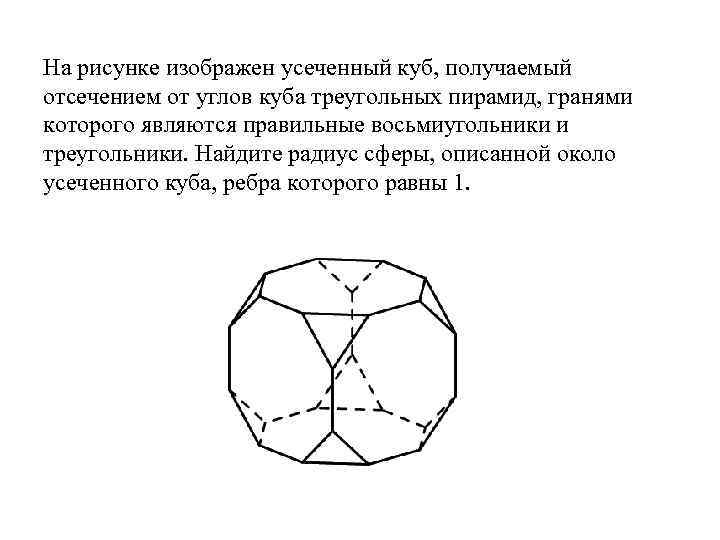
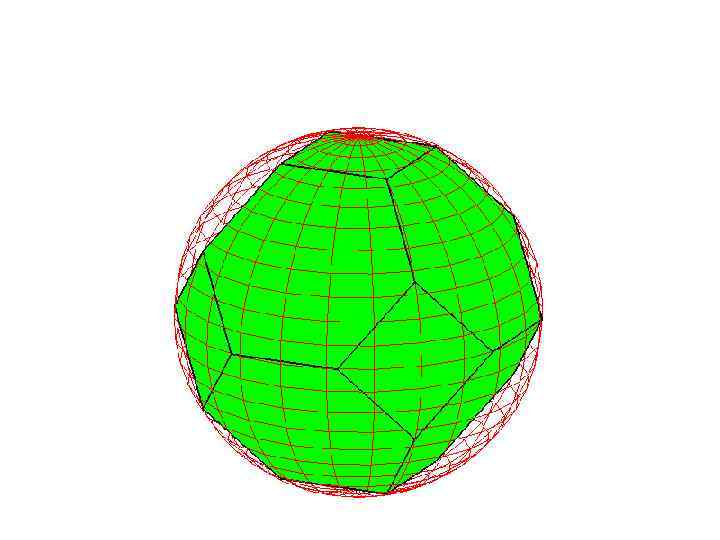
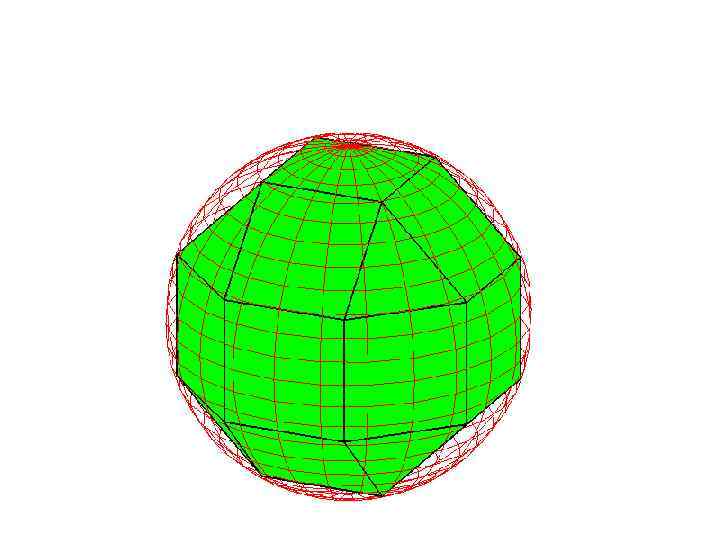
Сфера, описанная около усеченного куба

Упражнение

На рисунке изображен усеченный куб, получаемый отсечением от углов куба треугольных пирамид, гранями которого являются правильные восьмиугольники и треугольники. Найдите радиус сферы, описанной около усеченного куба, ребра которого равны 1.

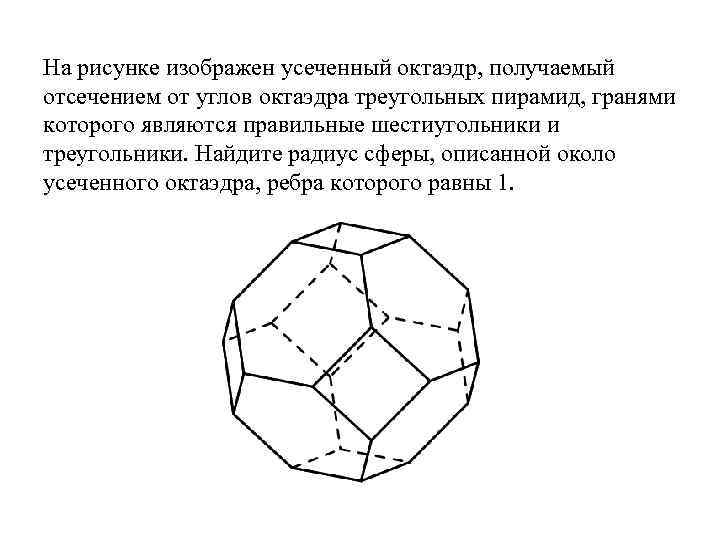
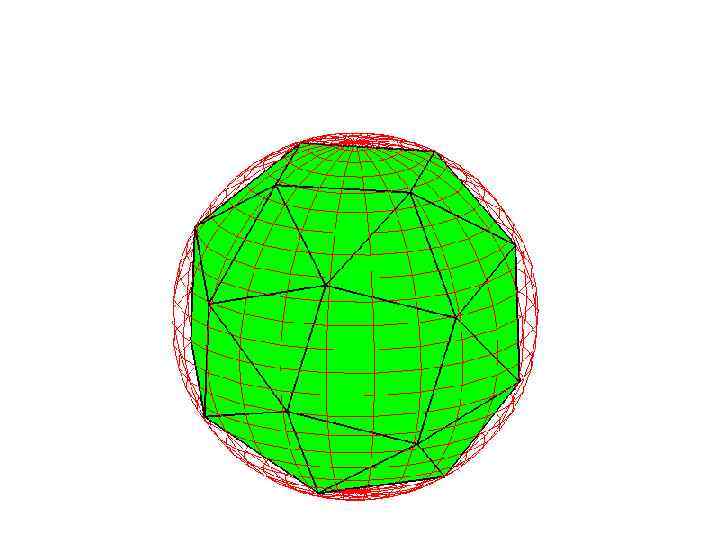
Сфера, описанная около усеченного октаэдра

Упражнение

На рисунке изображен усеченный октаэдр, получаемый отсечением от углов октаэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного октаэдра, ребра которого равны 1.

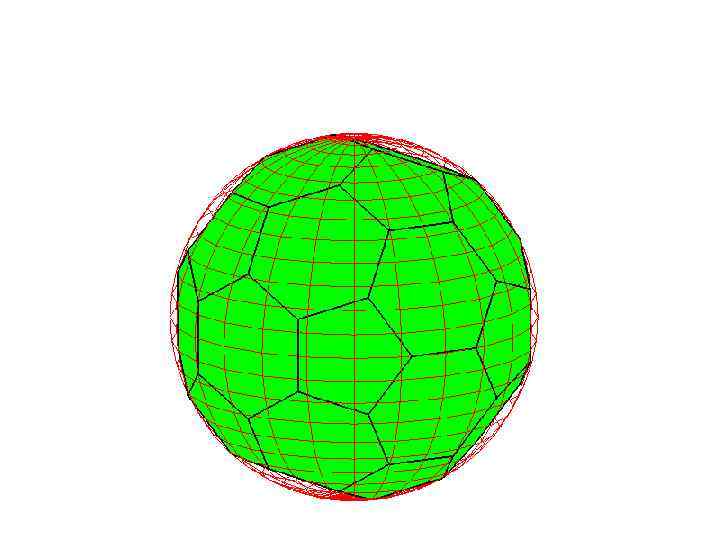
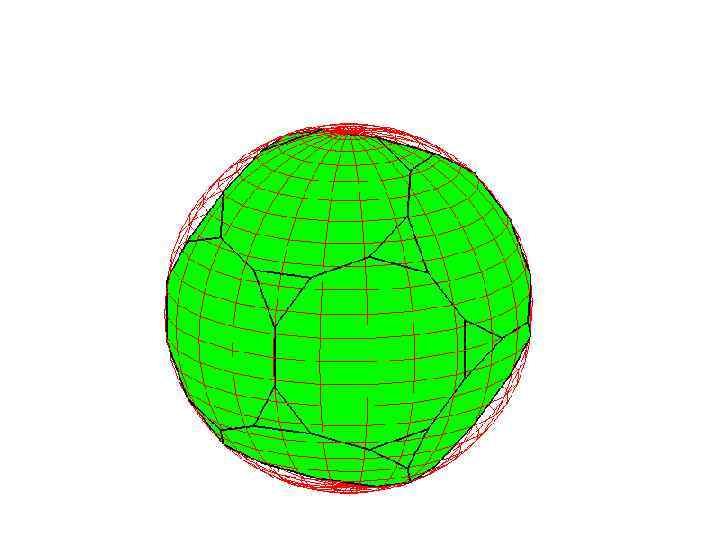
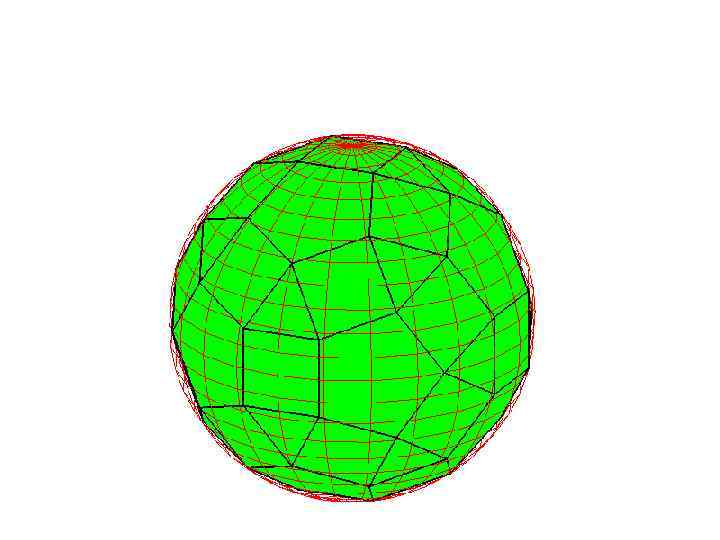
Сфера, описанная около усеченного икосаэдра

Упражнение

На рисунке изображен усеченный икосаэдр, получаемый отсечением от углов икосаэдра пятиугольных пирамид, гранями которого являются правильные шестиугольники и пятиугольники. Найдите радиус сферы, описанной около усеченного икосаэдра, ребра которого равны 1.

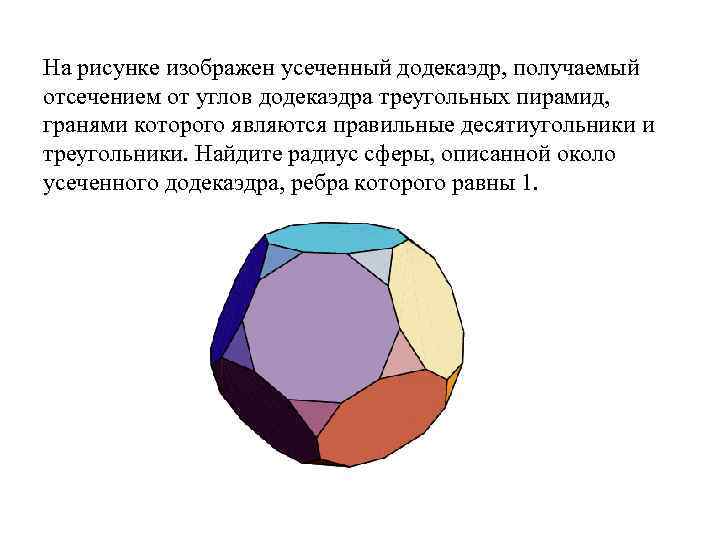
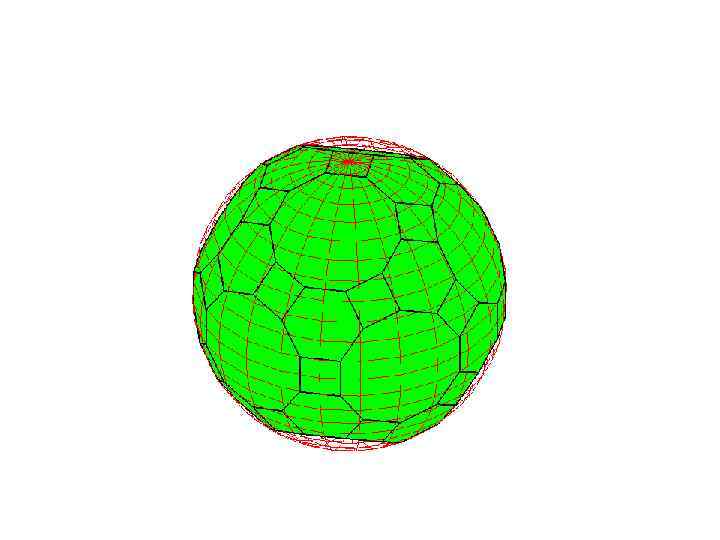
Сфера, описанная около усеченного додекаэдра

Упражнение

На рисунке изображен усеченный додекаэдр, получаемый отсечением от углов додекаэдра треугольных пирамид, гранями которого являются правильные десятиугольники и треугольники. Найдите радиус сферы, описанной около усеченного додекаэдра, ребра которого равны 1.

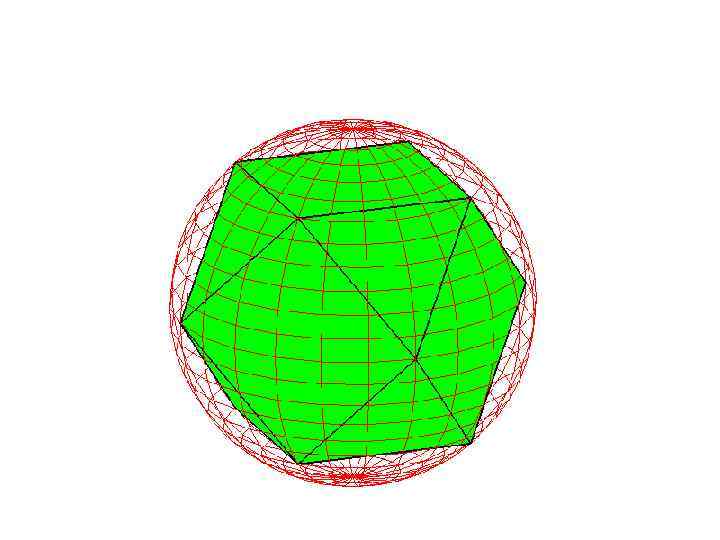
Сфера, описанная около кубооктаэдра

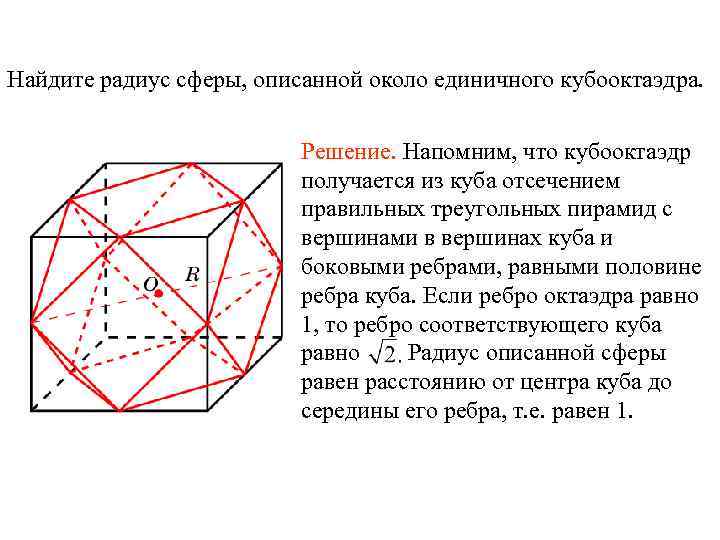
Упражнение

Найдите радиус сферы, описанной около единичного кубооктаэдра

Решение. Напомним, что кубооктаэдр получается из куба отсечением правильных треугольных пирамид с вершинами в вершинах куба и боковыми ребрами, равными половине ребра куба. Если ребро октаэдра равно 1, то ребро соответствующего куба равно Радиус описанной сферы равен расстоянию от центра куба до середины его ребра, т.е. равен 1.

Ответ: R = 1.

Сфера, описанная около икосододекаэдра

Сфера, описанная около усеченного кубооктаэдра

Сфера, описанная около усеченного икосододекаэдра

Сфера, описанная около ромбокубооктаэдра

Сфера, описанная около ромбоикосододекэдра

Сфера, описанная около курносого куба

Сфера, описанная около курносого додекэдра

Источник

I have a parallelepiped with sides, $a$, $b$, and $c$. $gamma$ is the angle between $a$ and $b$, $beta$ is the angle between $a$ and $c$, and $alpha$ is the angle between $b$ and $c$, as shown below:

My question is, under what circumstances would it be possible to inscribe a sphere into this parallelepiped? And if it is possible, can we express the sides of the parallelepiped in terms of the radius $r$ of the sphere and the angles?

Источник

Можно ли описать сферу около прямоугольного параллелепипеда? Ответ: Да. Ее центром является точка пересечения диагоналей, а радиус равен половине диагонали параллелепипеда.

Можно ли описать сферу около наклонного параллелепипеда, все грани которого ромбы? Ответ: Нет.

Можно ли описать сферу около наклонной призмы? Ответ: Нет.

Может ли центр сферы, описанной около призмы, находится вне призмы? Ответ: Да, если в основании призмы – тупоугольный треугольник.

Может ли центр сферы, описанной около пирамиды, находится вне этой пирамиды? Ответ: Да.

Найдите радиус сферы, описанной около единичного куба. Ответ:

Найдите ребро куба, вписанного в единичную сферу. Ответ:

Найдите радиус сферы, описанной около прямоугольного параллелепипеда, ребра которого, выходящие из одной вершины, равны 1, 2, 3. Ответ:

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 2. Радиус описанной сферы равен 1, 5. Найдите третье ребро, выходящее из той же вершины параллелепипеда. Ответ: 2.

Найдите радиус сферы, описанной около единичного тетраэдра.

Найдите ребро правильного тетраэдра, вписанного в единичную сферу. Ответ:

Найдите радиус сферы, описанной около правильной призмы, все ребра которой равны 1. Ответ:

Около правильной треугольной призмы, сторона основания которой равна 1, описана сфера радиуса 2. Найдите высоту призмы. Ответ:

Около правильной треугольной призмы, высота которой равна 1, описана сфера радиуса 1. Найдите сторону основания призмы. Ответ:

Найдите радиус сферы, описанной около прямой треугольной призмы, в основании которой прямоугольный треугольник с катетами, равными 1, и высота призмы равна 2. Ответ:

Найдите радиус сферы, описанной около правильной шестиугольной призмы, все ребра которой равны 1. Ответ:

Найдите радиус сферы, описанной около правильной четырехугольной пирамиды, все ребра которой равны 1. Ответ:

Найдите радиус сферы, описанной около правильной 6 -угольной пирамиды, ребра основания которой равны 1, а боковые ребра — 2.

Найдите радиус сферы, описанной около единичного октаэдра.

Найдите радиус сферы, описанной около единичного икосаэдра.

Найдите радиус сферы, описанной около единичного додекаэдра.

Найдите радиус сферы, описанной около единичного кубооктаэдра. Решение. Напомним, что кубооктаэдр получается из куба отсечением правильных треугольных пирамид с вершинами в вершинах куба и боковыми ребрами, равными половине ребра куба. Если ребро октаэдра равно 1, то ребро соответствующего куба равно Радиус описанной сферы равен расстоянию от центра куба до середины его ребра, т. е. равен 1.

Источник