Как найти радиус сферы вписанной в цилиндр - Исправление недочетов и поиск решений вместе с Examum.ru

В данной публикации мы рассмотрим, чему равняется радиус вписанного в прямой цилиндр шара или сферы. Информация сопровождается рисунками для лучшего восприятия.

Нахождение радиуса шара/сферы
- 1. Шар/сфера касается обоих оснований и боковой поверхности цилиндра
- 2. Шар/сфера касается только оснований цилиндра
- 3. Шар/сфера касается только боковой поверхности цилиндра

Нахождение радиуса шара/сферы

Радиус зависит от того, как именно шар (сфера) вписан в цилиндр. Сделать это можно тремя способами:

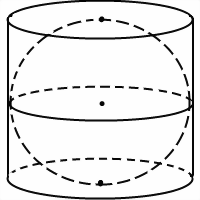
1. Шар/сфера касается обоих оснований и боковой поверхности цилиндра

Радиус (R) равен половине высоты цилиндра (h), а также радиусу (R) его основания.
Диаметр (d) шара равняется двум его радиусам (R) или высоте (h) цилиндра.

2. Шар/сфера касается только оснований цилиндра

Радиус (R) составляет половину высоты (h) цилиндра.

3. Шар/сфера касается только боковой поверхности цилиндра

В данном случае радиус (R) шара равняется радиусу (R) оснований цилиндра.

Примечание: еще раз подчеркнем, что вышеизложенная информация применима только к прямому цилиндру.

Источник

Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого круга (то есть радиус этой окружности равен радиусу шара).

Если шар вписан в цилиндр, то цилиндр описан около шара.

В цилиндр можно вписать шар тогда и только тогда, когда цилиндр равносторонний, то есть его высота равна диаметру. Радиус вписанного в цилиндр шара R равен радиусу цилиндра r:

R=r.

Решение задач на шар, вписанный в цилиндр, чаще всего сводится к рассмотрению осевого сечения комбинации тел.

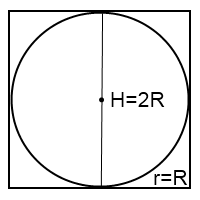
Это сечение представляет собой квадрат с вписанной в него окружностью. Сторона квадрата равна высоте цилиндра и диаметру шара:

H=2R

Найдем отношение объема цилиндра к объему вписанного в него шара. Объем шара

$[{V_1} = frac{4}{3}pi {R^3}]$

Объем цилиндра

$[{V_2} = pi {r^2}H = pi {R^2} cdot 2R = 2pi {R^3}.]$

Отсюда отношение объема шара к объему описанного около него цилиндра

$[frac{{{V_1}}}{{{V_2}}} = frac{{frac{4}{3}pi {R^3}}}{{2pi {R^3}}} = frac{2}{3}.]$

Теперь найдем отношение площади поверхности цилиндра к площади вписанного шара. Площадь поверхности шара (площадь сферы)

$[{S_1} = 4pi {R^2}]$

Площадь полной поверхности цилиндра равна сумме площадей оснований и боковой поверхности:

$[{S_2} = {S_{bok}} + 2{S_{ocn}} = 2pi rH + 2pi {r^2} = ]$

$[ = 2pi R cdot 2R + 2pi {R^2} = 6pi {R^2}.]$

Отсюда отношение площади поверхности вписанного шара к площади поверхности цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{4pi {R^2}}}{{6pi {R^2}}} = frac{2}{3}.]$

Источник

Скачать материал

Сейчас обучается 268 человек из 65 регионов

Сейчас обучается 387 человек из 62 регионов

Описание презентации по отдельным слайдам:

1 слайд

Сфера, вписанная в цилиндр
Сфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.
В цилиндр можно вписать сферу, если высота цилиндра равна
диаметру его основания.
Ее центром будет точка O, являющаяся
серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
Радиус сферы R будет равен
радиусу окружности основания цилиндра.
2 слайд

Упражнение 1
В цилиндр высоты 2 вписана сфера. Найдите ее радиус.
Ответ: 1.
3 слайд

Упражнение 2
В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.
Ответ: 2.
4 слайд

Упражнение 3
Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать сферу?
Ответ: 4.
5 слайд

Упражнение 4
Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра, чтобы в него можно было вписать сферу?
Ответ: 1.
6 слайд

Упражнение 5
Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2. Можно ли в этот цилиндр вписать сферу?
Ответ: Нет.
7 слайд

Упражнение 6
Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр вписать сферу?
Ответ: Да.
8 слайд

Упражнение 7
Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб?
Ответ: Нет.
9 слайд

Упражнение 8
Можно ли вписать сферу в наклонный цилиндр?
Ответ: Нет.
10 слайд

Упражнение 9
Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см2. Найдите диаметр сферы.
Ответ: 2 см.
11 слайд

Упражнение 10
Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.
Ответ: 1 см.
12 слайд

Упражнение 11
Какой наибольший радиус может быть у сферы, помещающейся в цилиндр, радиус основания которого равен 2, и высота 1.
Ответ: 0,5 см.
13 слайд

Упражнение 12
Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Ответ: Нет.
14 слайд

Упражнение 13
Какой наибольший радиус может быть у сферы, помещающейся в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Ответ:
15 слайд

Сфера, описанная около цилиндра
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.
Около любого цилиндра можно описать сферу. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
Радиус сферы R вычисляется по формуле

где h – высота цилиндра, r – радиус окружности основания.
16 слайд

Упражнение 1
Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной около этого цилиндра.
Ответ: 1.
17 слайд

Упражнение 2
Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.
Ответ:
18 слайд

Упражнение 3
Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.
Ответ:
19 слайд

Упражнение 4
Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.
Ответ:
20 слайд

Упражнение 5
Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60о.
Ответ:
21 слайд

Цилиндр, вписанный в призму
Цилиндр называется вписанным в призму, если его основания вписаны в основания цилиндра. При этом, призма называется описанной около цилиндра
В призму можно вписать цилиндр тогда и только тогда, когда
в ее основание можно вписать окружность.
Радиус основания цилиндра равен
радиусу окружности, вписанной в основание призмы.
Высота цилиндра равна
высоте призмы.
22 слайд

Упражнение 1
Можно ли вписать цилиндр в наклонную призму?
Ответ: Да, наклонный цилиндр.
23 слайд

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ:
24 слайд

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ: 2.
25 слайд

Упражнение 4
Найдите радиус окружности основания цилиндра, вписанного в единичный куб.
Ответ:
26 слайд

Упражнение 5
В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ:
27 слайд

Цилиндр, описанный около призмы
Цилиндр называется описанным около призмы, если его основания описаны около оснований цилиндра. При этом, призма называется вписанной в цилиндр
Около призмы можно описать цилиндр, если около ее оснований можно описать окружности.
Высота цилиндра равна
высоте призмы.
радиусу окружности, описанной около основания призмы.
Радиус основания цилиндра равен
28 слайд

Упражнение 1
Можно ли описать цилиндр около наклонной призмы?
Ответ: Да, наклонный цилиндр.
29 слайд

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:
30 слайд

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ: 5.
31 слайд

Упражнение 4
В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:
32 слайд

Упражнение 5
Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ: 1.
33 слайд

Упражнение 6
Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:
34 слайд

Упражнение 7
Около единичного октаэдра описан цилиндр так, что две противоположные вершины октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 268 178 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

27.12.2020
3413
1

27.12.2020
4791
2

27.12.2020
5028
13

27.12.2020
5844
13

27.12.2020
5082
9

27.12.2020
4081
1

27.12.2020
3904
0

27.12.2020
3928
1

Вам будут интересны эти курсы:

Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
Курс повышения квалификации «Основы туризма и гостеприимства»
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
Курс повышения квалификации «Экономика: инструменты контроллинга»
Курс повышения квалификации «Финансы: управление структурой капитала»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс повышения квалификации «Методы и инструменты современного моделирования»
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»

Источник

Шар является описанным около куба, если все вершины куба находятся на поверхности шара.

Центр шара (O) — точка пересечения диагоналей куба.

Около любого куба можно описать шар.

Общие точки шара и куба — восемь вершин куба.

Чертится диагональное сечение.

AC1

CA1

— диагонали куба.

Радиус шара равен половине диагонали куба.

Шар является вписанным в куб, если он касается всех его граней.

Центр шара (O) находится в точке пересечения диагоналей куба.
В любой куб можно вписать шар.
Общие точки шара и куба — центры шести граней куба (точки касания шара и куба).

Чертится сечение плоскостью, которая параллельна грани куба и проходит через центр шара.

Радиус шара — половина стороны куба.

Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

Центр шара (O) находится в середине высоты цилиндра.

Общие элементы — две окружности.

Около любого цилиндра можно описать шар.

Чертится осевое сечение.

Радиус шара — половина диагонали осевого сечения цилиндра.

Шар является вписанным в цилиндр, если касается оснований цилиндра и всех его образующих.

Центр шара (O) — середина высоты цилиндра.

Осевое сечение — квадрат с вписанной в него окружностью.

Радиус шара равен радиусу цилиндра и половине высоты цилиндра.

Источник