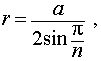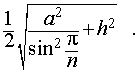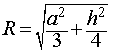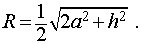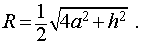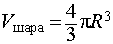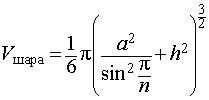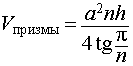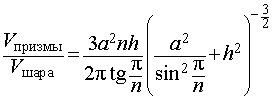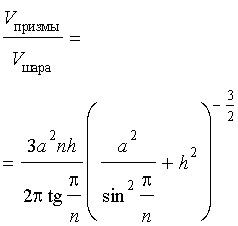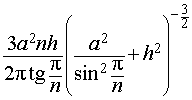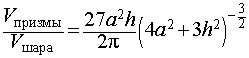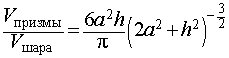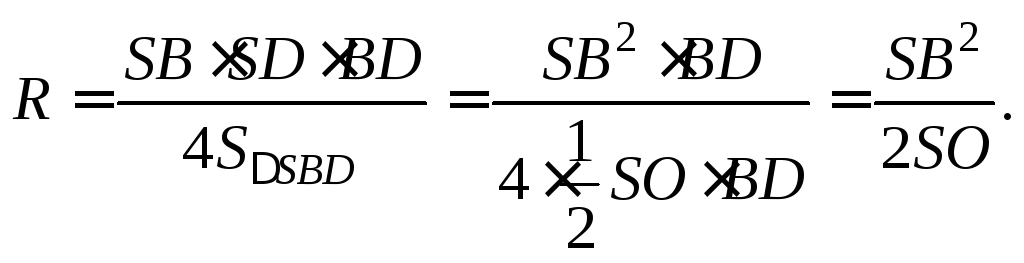Как найти радиус сферы вписанной в призму - Исправление недочетов и поиск решений вместе с Examum.ru

Призма, вписанная в сферу

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

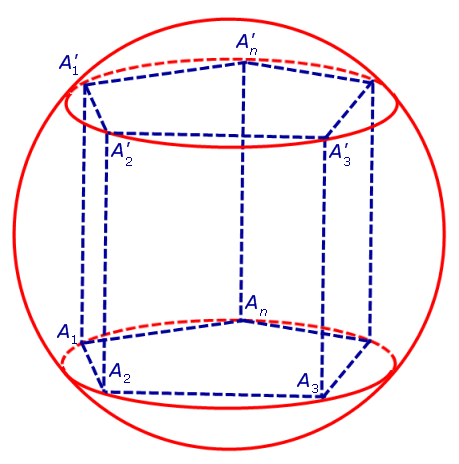
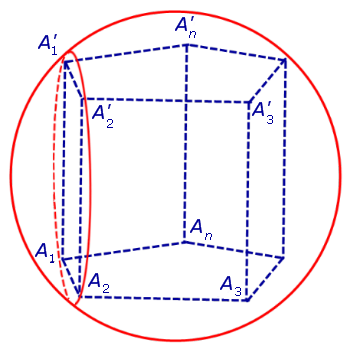
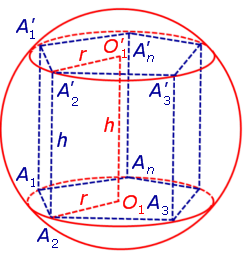
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.

Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если n – угольная призма A₁A₂ . A_nA’₁A’₂ . A’_n вписана в сферу, то оба условия теоремы выполнены.

Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.

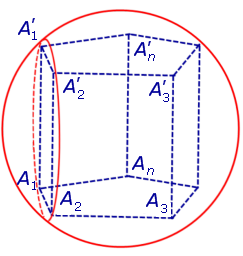
Каждая из боковых граней призмы также вписана в окружность (рис. 2).

Рассмотрим какое-нибудь боковое ребро призмы, например, A₂A’₂. Поскольку это ребро перпендикулярно к ребрам основания A₁A₂ и A₂A₃ , то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A₂A’₂ перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.

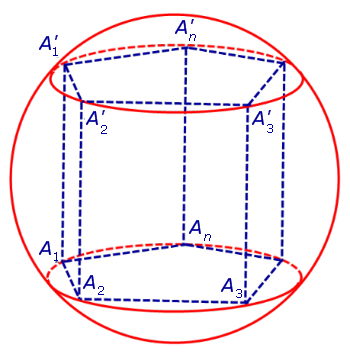
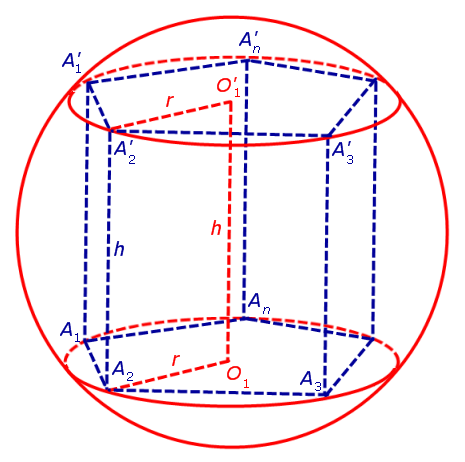
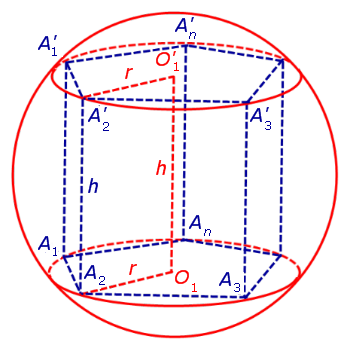
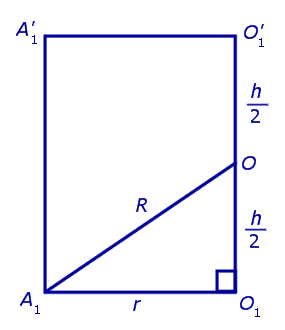
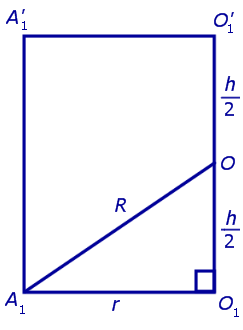
Для этого обозначим символом O₁ центр окружности радиуса r , описанной около нижнего основания призмы, а символом O’₁ обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.

Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O₁O’₁, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O₁O’₁ перпендикулярен плоскости основания призмы и равен h.

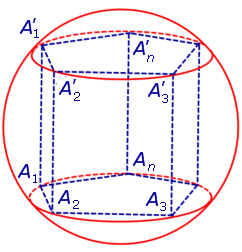
Обозначим буквой O середину отрезка O₁O’₁ и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).

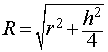(1)

от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.

Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.

Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать сферу.

Следствие 3. Около любой правильной призмы можно описать сферу.

Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.

Радиус сферы, описанной около правильной n — угольной призмы

то из формулы (1) получаем выражение для радиуса описанной сферы

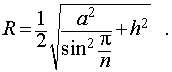(2)

Ответ.

Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен

Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около призмы сферой

Задача 2. Около правильной n — угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:

Ответ.

Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Радиус описанной сферы и ребро «A» треугольной призмы

Свойства

Зная радиус сферы, описанной вокруг правильной треугольной призмы с равносторонним треугольником в основании, можно найти сторону этого основания и затем посчитать высоту основания, радиусы вписанной и описанной окружностей около него, а также площадь. a=√(6/5) R_1 h=a/√2=√(3/5) R_1 r=a/(2√3)=2√(2/5) R_1 R=a/√3=√(2/5) R_1 S=(√3 a^2)/4=(3√3 〖R_1〗^2)/10

Боковое ребро треугольной призмы в совокупности с радиусом описанной сферы позволяет вычислить диагональ боковой стороны, периметр призмы и площадь боковой, а затем и полной поверхности призмы. d=√(a^2+b^2 )=√(6/5 〖R_1〗^2+b^2 ) P=3(2a+b)=3(2√(6/5) R_1+b) S_(б.п.)=3ab=3b√(6/5) R_1 S_(п.п.)=3b√(6/5) R_1+(3√3 〖R_1〗^2)/5

Чтобы найти объем треугольной призмы через радиус описанной сферы и боковое ребро, нужно подставить в формулу объема необходимое выражение вместо площади основания и умножить его на боковое ребро. V=S_(осн.) b=(3√3 〖R_1〗^2)/10 b

источники:

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

http://geleot.ru/education/math/geometry/calc/prism/radius_sphere_and_edge_a

Источник

meavis957

Вопрос по алгебре:

1)Найдите радиус сферы, вписанной в прямую призму ,высота которой равна h
2)Найдите радиус сферы ,вписанной в прямую призму ,в основании которой лежит ромб со стороной 4 и углом 60°

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

ngropromese

1)Если сфера вписана в призму,то ее диаметр равен высоте призмы,значит радиус равен половине высоты
R=h/2
2)Диаметр сферы равен высоте ромба и равен высоте призмы
Sр=4²sin60=16*√3/2=8√3
Sр=4*h
4h=8√3
h=2√3
R=√3

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат — это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Источник

Сфера
называется вписанной
в многогранник,
если она касается всех граней многогранника.

Многогранник
соответственно называется описанным
около сферы.

Теоремы:

Сферу можно вписать
в призму, если призма прямая и ее высота
равна диаметру окружности, вписанной
в основание призмы.
Сферу
можно вписать в пирамиду, если в основание
можно вписать окружность, а вершина
пирамиды ортогонально проектируется
в центр этой окружности.
Сферу можно вписать
в любую правильную пирамиду.

Сфера
называется вписанной
в цилиндр,
если она касается оснований и боковой
поверхности цилиндра. Цилиндр
соответственно называется описанным
около сферы.

Теорема.
Для того чтобы сферу можно было вписать
в цилиндр, необходимо и достаточно,
чтобы высота цилиндра равнялась диаметру
его основания.

Сфера
называется вписанной
в конус,
если она касается основания и боковой
поверхности конуса. Конус соответственно
называется описанным
около сферы.

Теорема.
Сферу можно вписать в любой конус.

Сфера
называется вписанной
в усеченный конус,
если она касается оснований и боковой
поверхности конуса. Усеченный конус
соответственно называется описанным
около сферы.

Теорема.
Для того чтобы сферу можно было вписать
в усеченный конус, необходимо и достаточно,
чтобы образующая усеченного конуса
равнялась сумме радиусов оснований.

Теорема.
Сферу можно вписать в тело вращения,
если в осевое сечение можно вписать
окружность.

Сфера,
описанная около многогранника

или
тела вращения

Сфера
называется описанной
около многогранника,
если все вершины многогранника лежат
на сфере. Многогранник соответственно
называется вписанным
в сферу.

Теоремы:

1. Для
того чтобы сферу можно было описать
около призмы, необходимо и достаточно,
чтобы призма была прямая и около основания
можно было описать окружность.

2. Для
того чтобы сферу можно было описать
около пирамиды, необходимо и достаточно,
чтобы около основания можно было описать
окружность.

3.
Сферу можно описать около любой правильной
пирамиды.

Сфера
называется описанной
около цилиндра,
если окружности оснований цилиндра
лежат на сфере. Цилиндр соответственно
называется вписанным
в сферу.

Теорема.
Сферу можно описать около любого
цилиндра.

Сфера
называется описанной
около конуса,
если окружность основания и вершина
конуса лежат на сфере. Конус соответственно
называется вписанным
в сферу.

Теорема.
Сферу можно описать около любого конуса.

Сфера
называется описанной
около усеченного конуса,
если окружности оснований конуса лежат
на сфере. Усеченный конус соответственно
называется вписанным
в сферу.

Теорема.
Сферу можно описать около любого
усеченного конуса.

Многогранники и тела вращения

Цилиндр
называется описанным
около призмы,
если окружности оснований цилиндра
описаны около оснований призмы, а боковые
ребра призмы являются образующими
цилиндра. Призма соответственно
называется вписанной
в цилиндр.

Теорема.
Для того чтобы около призмы можно было
описать цилиндр, необходимо и достаточно,
чтобы призма была прямая и около ее
основания можно было описать окружность.

Цилиндр
называется вписанным
в призму,
если окружности его оснований вписаны
в основания призмы, а боковая поверхность
касается боковых граней призмы.

Теорема.
Для того чтобы в призму можно было
вписать цилиндр, необходимо и достаточно,
чтобы призма была прямая и в ее основание
можно было вписать окружность.

Конус
называется описанным
около пирамиды,
если окружность основания конуса описана
около основания пирамиды, а боковые
ребра пирамиды являются образующими
конуса. Пирамида соответственно
называется вписанной
в конус.

Теорема.
Для того чтобы около пирамиды можно
было описать конус, необходимо и
достаточно, чтобы боковые ребра пирамиды
были равны.

Конус
называется вписанным
в пирамиду,
если окружность его основания вписана
в основание пирамиды, а боковая поверхность
касается боковых граней пирамиды.
Пирамида соответственно называется
описанной
около конуса.

Теорема.
Для того чтобы в пирамиду можно было
вписать конус, необходимо и достаточно,
чтобы в основание пирамиды можно было
вписать окружность, а вершина пирамиды
ортогонально проектировалась в центр
этой окружности.

Пример 1.
Шар вписан в прямую призму, основанием
которой является прямоугольный
треугольник с катетом a
и противолежащим ему острым углом α.
Найти объем призмы.

Решение. Сделаем
рисунок (рис. 12.48). Шар вписан в прямую
призму, значит, высота призмы равна
диаметру шара, а в треугольник основания
вписана окружность, радиус которой
равен радиусу шара. Рассмотрим
прямоугольный треугольник ABC,
у которого катет BC
= a,
противолежащий ему BAC =
α. Найдем катет AC
и гипотенузу AB:

Рис. 12.48

Площадь треугольника ABC
равна:

Вычислим радиус окружности, вписанной
в треугольник:

Вычисляем объем призмы по
формуле

Получаем ответ:

Пример 2.
Боковое ребро правильной четырехугольной
пирамиды равно a.
Двугранный угол, образованный смежными
боковыми гранями, равен β.
Найти радиус шара, описанного около
этой пирамиды.

Решение.
Сделаем рисунок (рис. 12.49): ABCD
– квадрат, SO
– высота пирамиды, AEC
= 
– двугранный угол.

Рассмотрим диагональное
сечение пирамиды – треугольник SBD
(SB = SD).
Радиусом шара, описанного около данной
пирамиды, будет радиус окружности,
описанной около треугольника SBD.
Найдем его по формуле

Рис. 12.49

Из подобия треугольников
(SOB = SEO
= 90,
BSO = OSE)
следует пропорциональность сторон:
SB/SO
= BO/OE.

Из треугольника
найдемТак какАО = ВО,
то
Следовательно,

Вычисляем радиус окружности:

Получаем ответ:

Пример 3. В
усеченный конус вписан шар радиуса R.
Образующая конуса наклонена к плоскости
основания под углом .
Найти объем усеченного конуса.

Решение.Рассмотрим осевое
сечение конуса (рис. 12.50).

Рис. 12.50

Введем обозначения: R₁
– радиус нижнего основания конуса, R₂
– радиус верхнего основания. Высота
данного усеченного конуса будет равна
диаметру вписанного в него шара 2R.
Рассмотрим прямоугольный треугольник
ABC:
B = 90,
A = ,
BC = 2R.
Найдем катет BA
и гипотенузу AC:
BA = BC  ctg,
Так как в усеченный конус вписан шар,
то образующая этого конуса равна сумме
радиусов его оснований. Получим равенство:

Заметим, что

Решив систему

найдем

Вычисляем объем усеченного конуса по
формуле (12.8).

Получаем ответ:

Пример 4. В
шар радиуса R
вписан конус, образующая которого
составляет с плоскостью основания угол
φ. Найти
площадь полной поверхности конуса.

Решение.
Для вычисления площади полной поверхности
конуса необходимо знать радиус основания
и образующую конуса. Рассмотрим осевое
сечение данного конуса – равнобедренный
треугольник SAB:
SA = SB
– образующие, SD
– высота, DB
– радиус основания конуса (рис. 12.51).

Рис. 12.51

По условию задачи SAD = φ,
следовательно,
ТреугольникAOS
– равнобедренный (AO = OS = R),
поэтому

Внешний угол этого треугольника при
вершине О
равен: AOD = SAO + ASO = 
– 2.

Из
треугольника AOD
(D = 90,
AO = R,
AOD = 
– 2)
выразим AD:

Из треугольника ASD
(D = 90,
AD = Rsin
2)
выразим SA:

Подставив найденные выражения
в формулу для вычисления площади полной
поверхности конуса, получим:

Таким образом,

Пример 5. В
прямой параллелепипед вписан цилиндр,
объем которого в m
раз меньше объема параллелепипеда.
Найти двугранные углы при боковых ребрах
параллелепипеда.

Решение.Двугранными углами при
боковых ребрах данного параллелепипеда
являются углы параллелограмма, лежащего
в его основании. В параллелепипед вписан
цилиндр, значит, в параллелограмм
основания вписана окружность. Если в
четырехугольник вписана окружность,
то суммы длин противолежащих сторон
четырехугольника равны. Таким образом,
основанием параллелепипеда является
ромб. Сделаем рисунок (рис. 12.52).

Рис. 12.52

Обозначим искомый угол .
Из треугольника ABC
(C = 90,
A = )
найдем сторону ромба AB
и его высоту BC:

Так как высоты цилиндра и
параллелепипеда равны, то площадь
основания цилиндра будет в m
раз меньше площади основания
параллелепипеда. Запишем равенство:
и выразим из негодалее

Двугранные
углы при боковых ребрах параллелепипеда
будут равны:

Задания

Соседние файлы в папке Часть 2

Источник

Описание презентации по отдельным слайдам:

1 слайд

Сфера, вписанная в многогранник
2 слайд

Сфера, вписанная в многогранник
Определение
Многогранник называется описанным около сферы(а сфера вписанной в многогранник), если все грани многогранника касаются этой сферы.
Следствие
Центр вписанной сферы есть точка, равноудаленная от всех граней многогранника.
3 слайд

Подготовительные задачи
1. Где расположено множество точек пространства , равноудаленных от двух плоскостей?
Теорема 1
Множество точек, равноудаленных от двух параллельных плоскостей ,есть плоскость, параллельная данным плоскостям и проходящая через середину общего перпендикуляра этих плоскостей.
Дано:
α || β;

γ|| α; γ|| β;
AC=CD; AB |α; AB| β
4 слайд

Теорема 2
Множество точек, равноудаленных от граней двугранного угла, есть есть биссектриса (биссекторная плоскость) этого двугранного угла.
5 слайд

Теорема 3
Множество точек, равноудаленных от граней трехгранного угла, есть биссектриса этого трехгранного угла.
Биссектрисой трехгранного угла называется луч с началом в вершине данного трехгранного угла, который образует равные углы с гранями этого трехгранного угла.
6 слайд

Сфера, вписанная в призму

Теорема 4

В призму можно вписать сферу тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, и высота призмы равна диаметру этой окружности (диаметру вписанной сферы).
7 слайд

2. Расстояние между боковыми ребрами треугольной призмы 13,14,15.В призму вписан шар. Боковое ребро составляет с плоскостью основания угол α . Найти объем призмы и объем шара.
Решение.
(А2В2С2)-перпендикулярное сечение.
Vш.= ⁴⁄₃ПR ш.3
S=⅟₂Prокр
R ш.=rвпис.окр.= S А2В2С2 /p
p =21;
S=√p(p-a) (p-b) (p-c);
S А2В2С2=84;
R ш.=84/21=4;
Vш.= ⁴⁄₃ПR ш.3; Vш.= 256П/3;
2) V пр.=S перп.сеч.*АА1 ;

АА1 =А1О/sin α=8/ sin α;

V пр.=84*8/ sin α =672/ sin α.

Ответ: 256П/3; 672/ sin α.
8 слайд

Сфера, вписанная в пирамиду
Боковые грани пирамиды одинаково наклонены к основанию.
Теорема 5
Если боковые грани пирамиды одинаково наклонены к основанию(двугранные углы при основании пирамиды равны), то в пирамиду можно вписать сферу, центр которой находится в точке пересечения высоты пирамиды и биссектрисы двугранного угла при основании пирамиды.
9 слайд

3.Основание пирамиды- треугольник со сторонами 9,10 и 17.Все боковые грани наклонены под углом 45о к основанию пирамиды .Найти радиус вписанного шара.
Решение.

1)OK= rвпис.окр. =S/p;
S=p* rвпис.окр . ;p=18;
S=√p(p-a) (p-b) (p-c);
S ∆АВС=36;OK=2.
2) ∆POK: KOш.-биссектриса, т.о.
ООш./Ош.p=OK/PK=cos 45о ;
ООш./Ош.p=1/ √2;
<PKO=45о ,т.е.ОК=ОР=2
⅟₂Rш-Rш.=1/ √ 2;
√ 2 Rш.=2-Rш.;
Rш.=2/(1+ √ 2)=2(√ 2-1).
Ответ: 2(√ 2-1).
10 слайд

Теорема 6
В любой тетраэд можно вписать сферу.
Теорема 7
Если в многогранник, объем которого равен V,а площадь поверхности равна S,вписан шар радиуса R,то имеет место соотношение:

V=⅓S*R
3.Основание пирамиды- треугольник АВС,В котором АВ|ВС,АВ=4,ВС=3.Боковое ребро РА перпендикулярно плоскости основания пирамиды и равно 3.Найдите объем шара, вписанного в пирамиду.
Решение.

1)Vпир.=⅓S ∆ ABC*AP;
Vпир.=⅓*⅟₂*3*4*3=6.
2)PB|BC(по теореме о трех перпендикулярах);АС=PB=5.
3) S ∆PАВ=S ∆АВС= ⅟₂*4*3=6.
S ∆PВC= S ∆PАC=⅟₂*3*5=7,5.
Sполн.=2*6+2*7,5=12+15=27.
4)Rш.=3 Vпир./S;
Rш.=3*6/27=⅔;
Vш.=⁴⁄₃ПR 3=32П/81.
Ответ: 32П/81.
11 слайд

4. Шар вписан в прямую призму, основание которой- равнобедренная трапеция с основаниями 2 и 8.Найдите объем шара и объем призмы.
Решение.

1)Rш.= rвпис.окр . ;Hпр.=D впис.окр.=CK.
2)DC+AB=AD+CB;
2BC=2+8; BC=5.
3)BC=⅟₂(AB-DC); BK= ⅟₂(8-2)=3;
4) ∆BCK:CK=4; Rш.=2.
5)Vпр.=Sосн.*Нпр.;
Vпр.=80;
Vш.= ⁴⁄₃ПR 3 ;
Vш.= ⁴⁄₃П2 3 =32П/3.
Ответ: 32П/3.
12 слайд

Спасибо за внимание

Источник

1)Найдите радиус сферы, вписанной в прямую призму , высота которой равна h 2)Найдите радиус сферы , вписанной в прямую призму , в основании которой лежит ромб со стороной 4 и углом 60°.

Перед вами страница с вопросом 1)Найдите радиус сферы, вписанной в прямую призму , высота которой равна h 2)Найдите радиус сферы , вписанной в прямую призму , в основании которой лежит ромб со стороной 4 и углом 60°?, который относится к
категории Алгебра. Уровень сложности соответствует учебной программе для
учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.

Источник