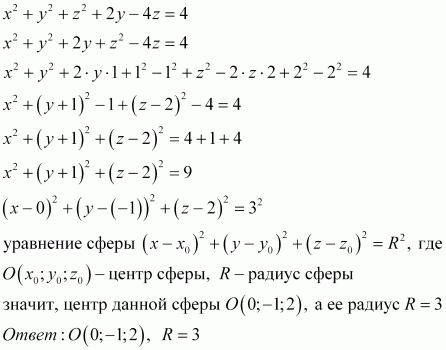Как найти радиус сферы заданной уравнением

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

• что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
• что такое шар и его элементы;
• уравнение сферы;
• формула для нахождения площади поверхности сферы;
• взаимное расположение сферы и плоскости;
• теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.

Глоссарий по теме:

Определение

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Определение

Круг – это часть плоскости, ограниченная окружностью.

Определение

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Определение

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Уравнение сферы

– уравнение сферы радиуса R и центром С(x₀; y₀; z₀).

Определение

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Определение

Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Определение

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Определение

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Определение

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

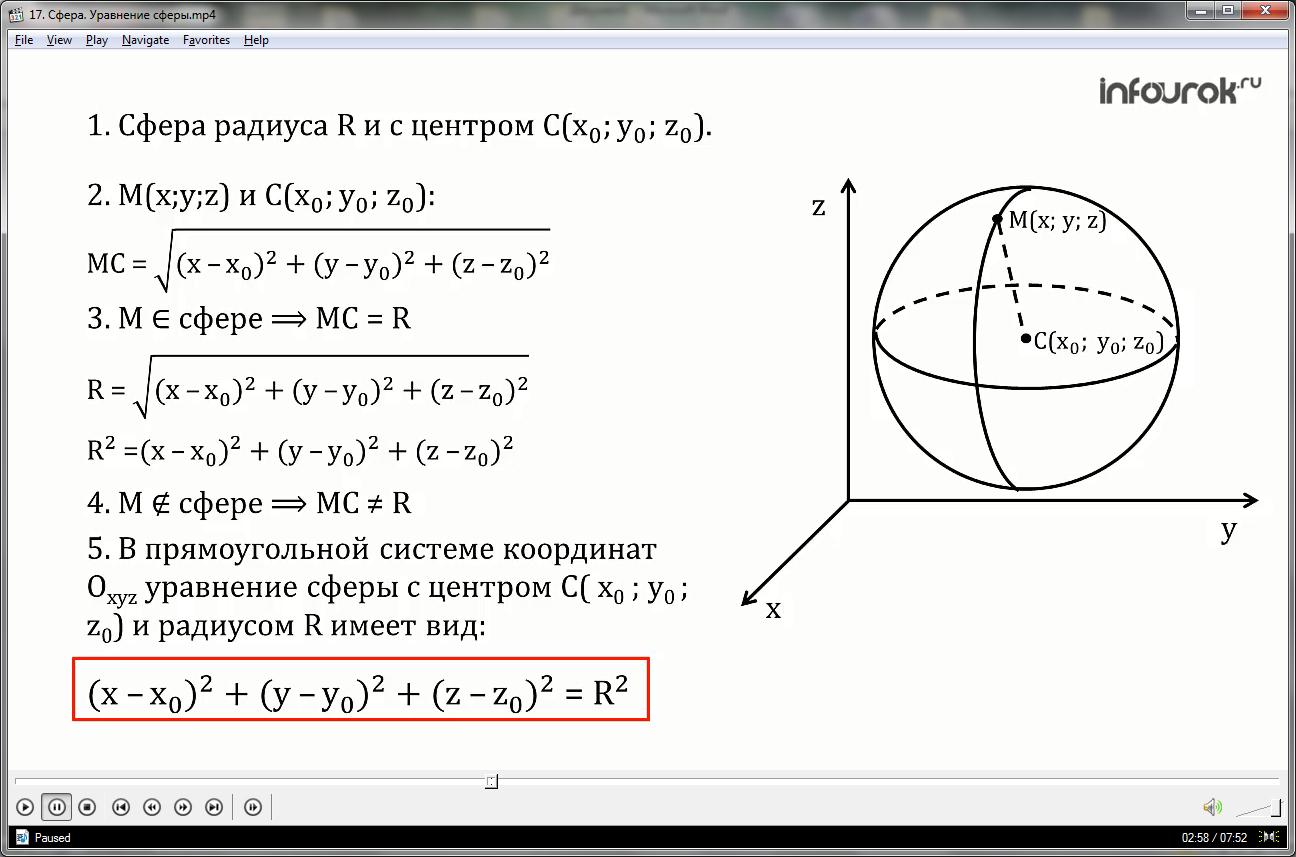
Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС²=R², то есть координаты точки М удовлетворяют уравнению:

.

Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Определение

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR² – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Решение:

Площадь круга вычисляется по формуле: S_кр=πR².

Площадь поверхности шара вычисляется по формуле: S_сф=4πR². Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

Ответ: 36

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Решение:

Площадь сферы равна S_сф=4πR². То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r² =100, то есть r=10.

Ответ: 10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Решение:

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

p=0,5(AB+BC+AC)=21

S=84.

С другой стороны, S=p·r.

Отсюда r=4.

Теперь найдем расстояние от центра шара до секущей плоскости.

Используем соотношение:

h=3.

Ответ: 3.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Решение:

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

По условию задачи R=10.

Используем соотношение:

h=6.

Ответ: 6.

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными  x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

1.Рассмотрим сферу радиуса R  и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

МС=√(x-x0)2+(y-y0)2+(z-z0)2.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

R=√(x-x0)2+(y-y0)2+(z-z0)2  или

R2=(x-x0)2+(y-y0)2+(z-z0)2 .

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит,  координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

(x-x0)2+(y-y0)2+(z-z0)2 = R2

Применим полученные знания при решении задач.

Задача 1.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

Решение:

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

(x-x0)2+(y-y0)2+(z-z0)2 = R2

2.Подставим соответствующие координаты центра сферы А в  данное уравнение:

(x+2)2+(y-2)2+(z-0)2 = R2

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

(x+2)2+(y-2)2+z2 = R2

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

R2=(5+2)2+(0-2)2+(-1)2 =49+4+1=54

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

(x+2)2+(y-2)2+z2 = 54

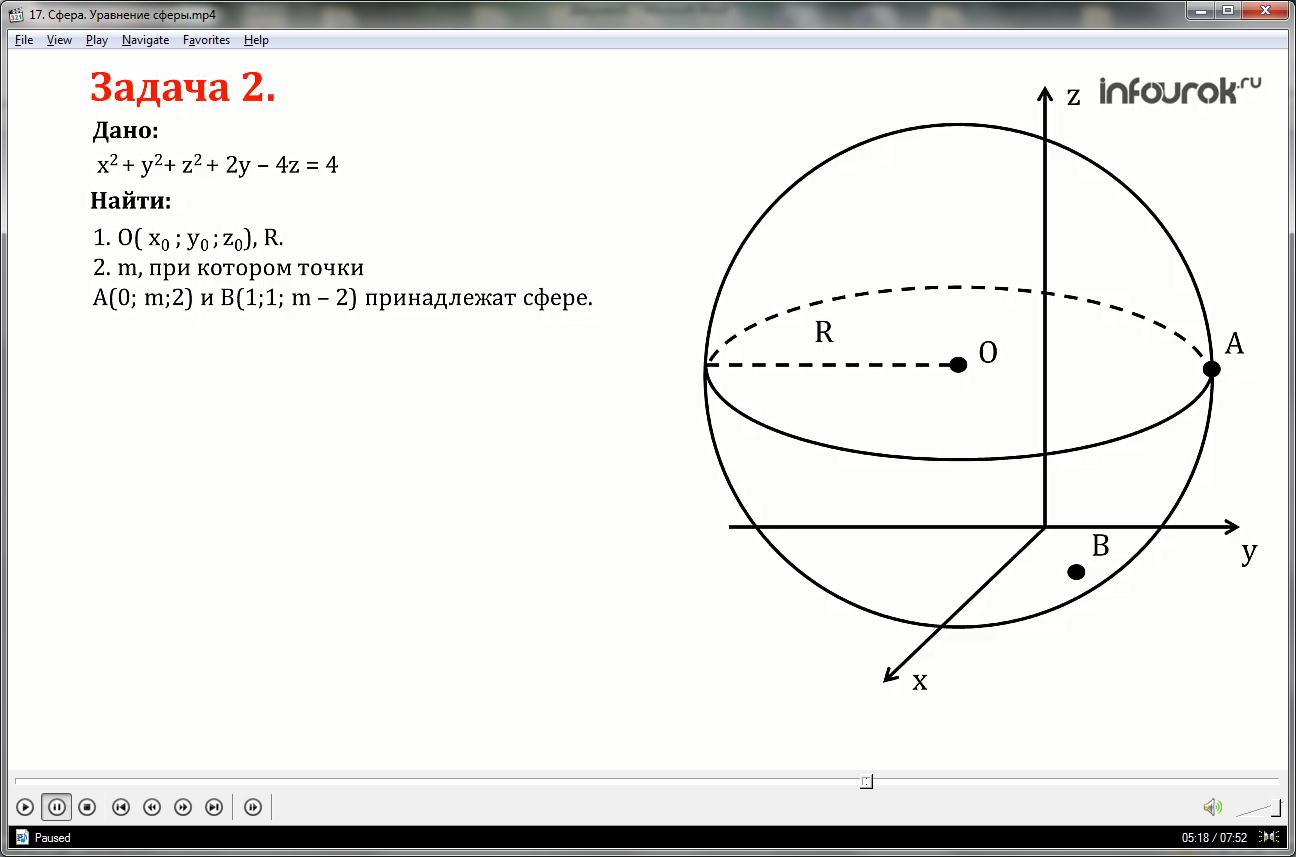
Задача 2.

Сфера задана уравнением:

x2+ y2+ z2+2y-4z=4

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

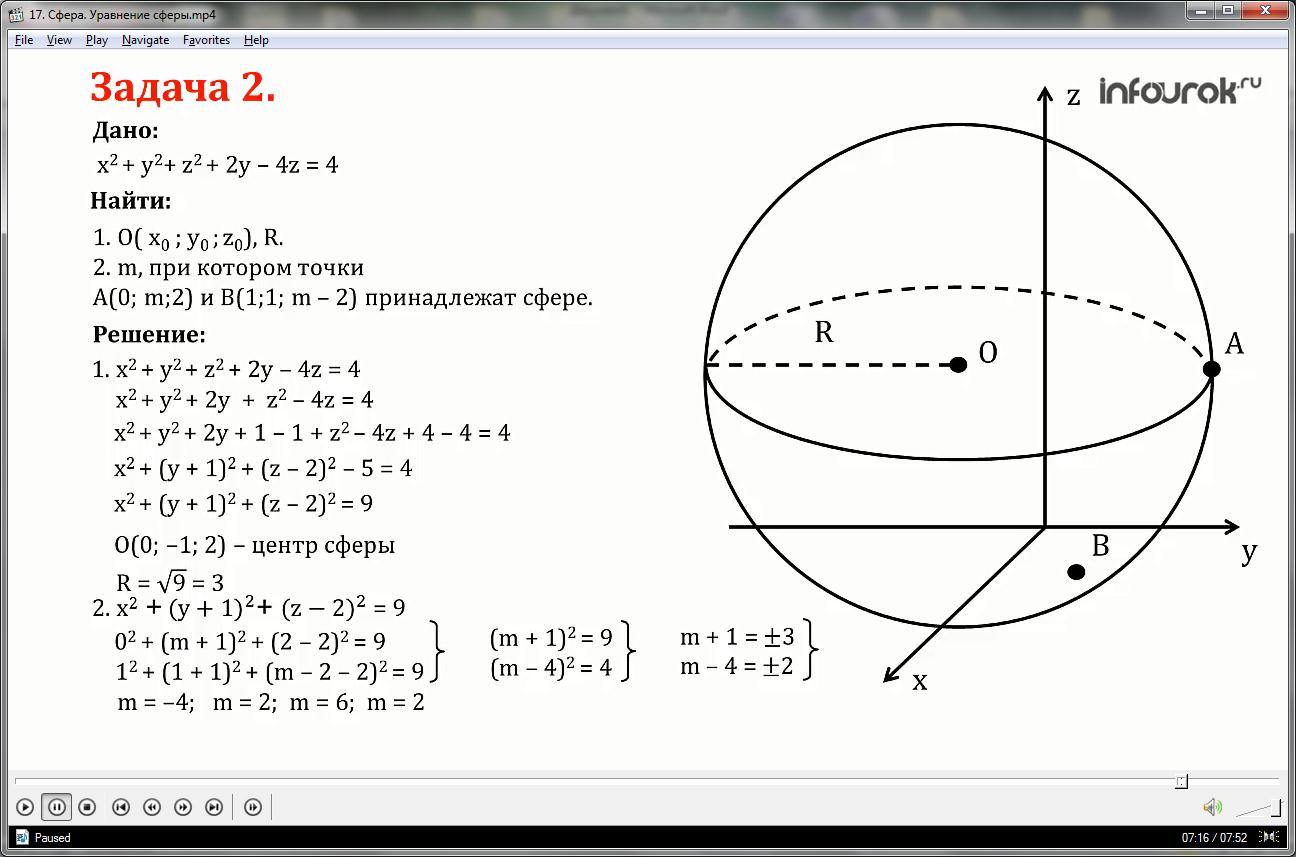
Решение:

1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

x2+( y+1)2+( z-2)2=9

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

x2+( y+1)2+( z-2)2=9

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

02+( m+1)2+(2-2)2=9

12+(1+1)2+( m-2-2)2=9

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

m=-4;   m=2;  m=6;  m=2.

Несложно проверить, что при  m=-4 и  m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

На этом уроке мы вспомним понятия сферы и шара. Дадим
их определения. Рассмотрим их основные элементы. А также выведем уравнение
сферы радиуса  с
центром в точке .

Итак, рассмотрим понятия сферы и шара. В окружающем
мире предметы имеют очень разнообразные формы. Среди них встречаются так
называемые «круглые тела». Особое место среди круглых тел занимает шар.

Итак, шар – это геометрическое тело.

Форму, близкую к форме шара, имеют шарики
мороженного, снежный ком, бусинки, светильники.

Некоторые архитектурные сооружения.

Декоративным растениям также придают форму шара.

Поверхность шара называют сферой. Можно
сказать, что сфера – это как-бы оболочка или граница шара. Как
окружность, есть граница круга, так и сфера – это граница шара.

Представление о сфере дают полые круглые
предметы, например, мячи (футбольный, баскетбольный, волейбольный и т.д.), шарики
для украшения ёлки, мыльные пузыри.

А также ставший популярным видом отдыха в наше время
«аквазорбинг». Зорб даёт представление о сфере.

Сфера входит в число наиболее привлекательных
пространственных фигур. Использование в строительстве и архитектуре
конструкций, имеющих форму сферы, придает сооружениям особое величие и служит
подтверждением тому, что сфера – достаточно гармоничная геометрическая фигура.

Чтобы уяснить разницу между понятиями шар и сфера,
давайте внимательно посмотрим на экран.

Перед вами изображены воздушный шар и бильярдный шар. Отметим,
что оба этих предмета называют шарами. Однако в первом случае мы имеем дело со
сферой, а во втором с полноценным шаром со своим содержимым внутри.

Определение:

Сферой
называется поверхность, состоящая из всех точек пространства, расположенных на
данном расстоянии от данной точки.

А теперь назовём основные элементы сферы.

Данная точка называется центром сферы (в
нашем случае это точка О), а данное расстояние – радиусом сферы.
Радиус сферы часто обозначают латинской буквой .

Любой отрезок, соединяющий центр и какую-нибудь точку
сферы, также называется радиусом сферы. Все радиусы одной сферы равны
между собой.

Хордой
сферы называется отрезок, соединяющий две точки сферы.

Отрезок, соединяющий две точки сферы и проходящий
через её центр, называется диаметром сферы. Любой диаметр сферы равен
двум радиусам .

Тело, ограниченное сферой, называется шаром.

Определение:

Шар – это
совокупность всех точек пространства, находящихся от центра на расстоянии, не
больше заданного.

Центр, радиус, хорда и диаметр сферы называются также
центром, радиусом, хордой и диаметром шара.

Т.е. отрезок, соединяющий любую точку сферы с центром
шара, называется радиусом шара.

Отрезок, соединяющий две точки сферы называется хордой
шара.

Отрезок, соединяющий две точки сферы и проходящий
через центр шара, называется диаметром шара. Диаметр шара равен двум
радиусам .

Рассмотрим чертёж.

Перед нами математическое изображение шара. Точка О –
это центр шара. Все точки поверхности шара одинаково удалены от
центра шара. Понятно, что шар радиуса  с
центром О содержит все точки пространства, расположенные от точки О на
расстоянии, не превышающем  (включая
саму точку О), и не содержит других точек.

Хотелось бы обратить внимание на то, что шар может
быть получен путём вращения полукруга вокруг его диаметра.

При этом сфера образуется в результате вращения
полуокружности вокруг её диаметра.

Задача: отрезок
 –
хорда сферы, не проходящая через центр сферы .
Вычислите расстояние от центра сферы до середины хорды ,
если радиус сферы равен  см,
а длина хорды  равна
 см.

Решение: обозначим
середину хорды  точкой
.

Рассмотрим .
Он равнобедренный, т.е. ,
так как .
А как мы знаем, все радиусы одной сферы равны между собой. Отсюда,  (см).

Теперь рассмотрим .
Он прямоугольный, так как отрезок  является
серединным перпендикуляром проведённым к хорде .
Его катет  (см).

Воспользовавшись теоремой Пифагора найдём катет ,
который как раз таки и есть расстояние от центра сферы до середины хорды .
Получаем, что  (см).

Запишем ответ.

Перейдём к уравнению сферы.

Для начала вспомним, что уравнение с тремя переменными
,
,
 называется
уравнением поверхности ,
если этому уравнению удовлетворяют координаты любой точки поверхности  и
не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

Напомним, что уравнение плоскости, проходящей через
точку  и
перпендикулярной к ненулевому вектору  имеет
следующий вид:

где

Теперь давайте выведем уравнение сферы радиуса  с
центром в точке .

Напомним, что расстояние от произвольной точки  до
точки  вычисляется
по формуле:

Если точка  лежит
на данной сфере, то расстояние ,
или ,
т.е. координаты точки  удовлетворяют
уравнению:

Если же точка  не
лежит на данной сфере, то расстояние ,
или ,
т.е. координаты точки  не
удовлетворяют уравнению сферы.

Следовательно, в прямоугольной системе координат
уравнение сферы радиуса  с
центром в точке :

Если уравнение относительно прямоугольных координат  определяет
поверхность в пространстве, то ею является сфера.

Задача: напишите
уравнение сферы с центром в точке  радиусом
равным  см.

Решение: запишем
уравнение сферы в общем виде, где ,
 и
 –
координаты центра сферы.

Подставим заданные координаты центра сферы в
уравнение. Получим, что уравнение данной нам сферы выглядит так:

Запишем ответ.

Задача: найдите
координаты центра и радиус сферы, заданной уравнением: .

Решение: запишем
уравнение сферы в общем виде, где ,
 и
 –
координаты центра сферы.

Тогда не трудно заметить, что координаты центра сферы
будут равны 2, — 1, 0.

А радиус заданной сферы равен .

Не забудем записать ответ.

Задача: какую
поверхность определяет уравнение

 ?

Решение: запишем
уравнение сферы в общем виде, где ,
 и
 –
координаты центра сферы.

Преобразуем наше уравнение.

Разделим почленно это уравнение на 4.

Получим, .

Затем выделим полные квадраты. Получим, .
 

Преобразуем слагаемые получившегося выражения.
Получим, .

Теперь сравним последнее уравнение с уравнением сферы
в общем виде. Заметим, что исходное уравнение определяет сферу с центром в
точке  и .

Запишем ответ.

Итоги:

На этом уроке мы вспомнили понятия сферы и шара. Узнали,
что сферой называется поверхность, состоящая из всех точек пространства,
расположенных на данном расстоянии от данной точки. А шар – это совокупность
всех точек пространства, находящихся от центра на расстоянии, не больше
заданного. Назвали основные элементы сферы и шара. А также вывели уравнение
сферы радиуса  с
центром в точке .

Учеба и наука

Вопрос задан анонимно


март 3, 2021 г.

• Всего ответов: 1

• 

  Лучший ответ по мнению автора

Похожие вопросы