Как найти радиус шара вписанного в цилиндр - Исправление недочетов и поиск решений вместе с Examum.ru

В данной публикации мы рассмотрим, чему равняется радиус вписанного в прямой цилиндр шара или сферы. Информация сопровождается рисунками для лучшего восприятия.

Нахождение радиуса шара/сферы
- 1. Шар/сфера касается обоих оснований и боковой поверхности цилиндра
- 2. Шар/сфера касается только оснований цилиндра
- 3. Шар/сфера касается только боковой поверхности цилиндра

Нахождение радиуса шара/сферы

Радиус зависит от того, как именно шар (сфера) вписан в цилиндр. Сделать это можно тремя способами:

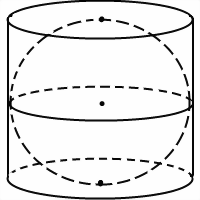
1. Шар/сфера касается обоих оснований и боковой поверхности цилиндра

Радиус (R) равен половине высоты цилиндра (h), а также радиусу (R) его основания.
Диаметр (d) шара равняется двум его радиусам (R) или высоте (h) цилиндра.

2. Шар/сфера касается только оснований цилиндра

Радиус (R) составляет половину высоты (h) цилиндра.

3. Шар/сфера касается только боковой поверхности цилиндра

В данном случае радиус (R) шара равняется радиусу (R) оснований цилиндра.

Примечание: еще раз подчеркнем, что вышеизложенная информация применима только к прямому цилиндру.

Источник

Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого круга (то есть радиус этой окружности равен радиусу шара).

Если шар вписан в цилиндр, то цилиндр описан около шара.

В цилиндр можно вписать шар тогда и только тогда, когда цилиндр равносторонний, то есть его высота равна диаметру. Радиус вписанного в цилиндр шара R равен радиусу цилиндра r:

R=r.

Решение задач на шар, вписанный в цилиндр, чаще всего сводится к рассмотрению осевого сечения комбинации тел.

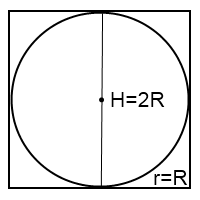
Это сечение представляет собой квадрат с вписанной в него окружностью. Сторона квадрата равна высоте цилиндра и диаметру шара:

H=2R

Найдем отношение объема цилиндра к объему вписанного в него шара. Объем шара

$[{V_1} = frac{4}{3}pi {R^3}]$

Объем цилиндра

$[{V_2} = pi {r^2}H = pi {R^2} cdot 2R = 2pi {R^3}.]$

Отсюда отношение объема шара к объему описанного около него цилиндра

$[frac{{{V_1}}}{{{V_2}}} = frac{{frac{4}{3}pi {R^3}}}{{2pi {R^3}}} = frac{2}{3}.]$

Теперь найдем отношение площади поверхности цилиндра к площади вписанного шара. Площадь поверхности шара (площадь сферы)

$[{S_1} = 4pi {R^2}]$

Площадь полной поверхности цилиндра равна сумме площадей оснований и боковой поверхности:

$[{S_2} = {S_{bok}} + 2{S_{ocn}} = 2pi rH + 2pi {r^2} = ]$

$[ = 2pi R cdot 2R + 2pi {R^2} = 6pi {R^2}.]$

Отсюда отношение площади поверхности вписанного шара к площади поверхности цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{4pi {R^2}}}{{6pi {R^2}}} = frac{2}{3}.]$

Источник

yover185

Вопрос по геометрии:

шар вписан в цилиндр,диагональ осевого сечения,которого равна 5 см. Найти радиус шара

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

gntegatsh723

Осевое сечение цилиндра в данном случае — квадрат.

Rш=a/2

2a^2=5^2

a^2=25/2

a=5/корень из 2=(5*корень из 2)/2

Rш=a/2=(5*корень из 2)/4

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат — это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Здравствуйте! В этой статье мы с вами рассмотрим задачи с шарами. Вернее здесь будет комбинация тел: шар вписанный в цилиндр или другими словами цилиндр описанный около шара (что одно и тоже) и куб вписанный в шар.

На блоге уже рассмотрена группа задач с шарами, посмотрите. В представленных заданиях речь пойдёт о нахождении объёма и площади поверхности указанных тел. Формулы которые необходимо знать!

Формула объёма шара:

Формула площади поверхности шара:

Формула объёма цилиндра:

Формула площади поверхности цилиндра:

Подробнее о площади боковой поверхности цилиндра:

Она представляет собой «скрученный» в цилиндр прямоугольник одна сторона которого равна длине окружности основания — это 2ПiR, другая сторона равна высоте цилиндра — это Н.

Что стоит отметить касаемо представленных задач?

1. Если шар вписан в цилиндр, то у них общий радиус.

2. Высота цилиндра описанного около шара равна двум его радиусам (или диаметру).

3. Если куб вписан в шар, то диагональ этого куба равна диаметру шара.

245348. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.

Формула объёма шара:

Необходимо найти радиус шара.

У шара и у цилиндра общий радиус. Основание цилиндра это круг с радиусом R, высота цилиндра равна двум радиусам. Значит объём цилиндра вычисляется по формуле:

Подставим данный в условии объём в формулу и выразим радиус:

Оставим выражение в таком виде, выражать радиус (извлекать корень третьей степени) не обязательно, так как нам понадобится именно R³.

Таким образом, объём шара будет равен:

Ответ: 22

245349. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Эта задача обратная предыдущей.

Формула объёма шара:

Объём цилиндра вычисляется по формуле:

Так как объём шара известен, то мы можем выразить радиус и уже далее найти объём цилиндра:

Таким образом:

Ответ: 36

316557. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

Формула поверхности шара:

Формула поверхности цилиндра:

Упростим:

Так как площадь поверхности шара нам дана, то мы можем выразить радиус:

Далее подставим его в формулу площади поверхности цилиндра и вычислить её, таким образом:

Ответ: 166,5

245355. Куб вписан в шар радиус которого равен корню из трёх. Найдите объем куба.

Чтобы вычислить объём куба необходимо знать чему равно его ребро. Радиус шара равен половине диагонали куба:

*Диагональ куба равна диаметру шара.

Значит диагональ куба будет равна двум корням из трёх. Обозначим диагональ буквой d, а ребро куба буквой a. Нам известна формула выражающая взаимосвязь диагонали куба и его ребра:

Значит мы можем вычислить ребро куба:

Таким образом, объём куба будет равен 2³ = 8.

Ответ: 8

Если подвести небольшой итог, то можно сказать следующее:

Используя указанные формулы при данных величинах объёма или площади поверхности всегда можно найти (выразить) радиус. А затем зная радиус, далее уже можно его использовать при вычислениях.

В любом случае знание формул обязательно!!! Без этого никак. На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Шар является описанным около куба, если все вершины куба находятся на поверхности шара.

Центр шара (O) — точка пересечения диагоналей куба.

Около любого куба можно описать шар.

Общие точки шара и куба — восемь вершин куба.

Чертится диагональное сечение.

AC1

CA1

— диагонали куба.

Радиус шара равен половине диагонали куба.

Шар является вписанным в куб, если он касается всех его граней.

Центр шара (O) находится в точке пересечения диагоналей куба.
В любой куб можно вписать шар.
Общие точки шара и куба — центры шести граней куба (точки касания шара и куба).

Чертится сечение плоскостью, которая параллельна грани куба и проходит через центр шара.

Радиус шара — половина стороны куба.

Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

Центр шара (O) находится в середине высоты цилиндра.

Общие элементы — две окружности.

Около любого цилиндра можно описать шар.

Чертится осевое сечение.

Радиус шара — половина диагонали осевого сечения цилиндра.

Шар является вписанным в цилиндр, если касается оснований цилиндра и всех его образующих.

Центр шара (O) — середина высоты цилиндра.

Осевое сечение — квадрат с вписанной в него окружностью.

Радиус шара равен радиусу цилиндра и половине высоты цилиндра.

Источник